表データ分析プロジェクトの道標
門脇大輔 阪田隆司 保坂桂佑 平松雄司 著
Kaggleで勝つデータ分析の技術
2019-10-09 技術評論社
https://gihyo.jp/book/2019/978-4-297-10843-4
Abhishek Thakur 著, 石原祥太郎 訳
Kaggle Grandmasterに学ぶ 機械学習 実践アプローチ (Approaching (Almost) Any Machine Learning Problem)
2021-08-24 マイナビ出版
https://book.mynavi.jp/ec/products/detail/id=123641
最近専ら理論重視の本を追っていたので、趣向を変えてデータコンペの定番書2冊(以下それぞれKDT, AAMLP)を読んだメモと思ったことを書いていきます。今回は各項目の理論には深入りせず、網羅的に薄く広い説明を置きます。
私がCV/NN屋ということもあり、数値データメインのtree系の手法の話などは特に新鮮で面白かったです。
TL;DR
- データセットの分割は、特徴量の分布が同じになるように、またはグループや時系列などの特性に応じて適切な分け方でk-foldすること。
- 学習データから検証データを分割する場合、テストデータを使ったAdversarial Validationを行うと、テストデータとの分布の違いがあるかどうかわかる。
- クロスバリデーションで、ついでにout-of-foldな特徴量スタッキングなどもできる。
- TP/(TP+FN)とFP/(TP+FP)のROC曲線、その面積AUCはモデルの精度を適切に測る確率として機能する。
- モデルの予測値と評価指標の中間にハイパラメータがある場合、評価指標を使った最適化がある。
- GBDTは簡単に使えて精度も出るので良い。
特徴量エンジニアリングについては次の記事に分割した。
遊ぶためのデータセットとしてRに付属するものが使える。 [解説] [データ]
この記事では次のライブラリを使います。
import numpy as np
import polars as pl
import matplotlib.pyplot as plt
import seaborn as sns
モデル作成の進め方
- タスク理解: 今から作るモデルの入出力、データの内容、KPIなどの評価指標を理解するため、探索的データ分析(Explorationry Data Analysis; EDA)を行う。EDAでは仮説(モデル)などを立てる前に、データの型や値の分布、欠損、外れ値、各データの相関などを広く浅く調べて、グラフやt-SNEによるクラスタ可視化などを行う。
- 特徴量の作成: データを整形してモデルへの入力を作る。例えば生のデータでは予測に関係ない行IDなどが含まれていることもあるので、それを削除したり、カテゴリデータをone-hot化したり、欠損を上手く扱えないモデルを使う場合は欠損値の埋め方を検討したりする。
- 特徴量を学習データと検証データに分割し、モデルを学習させる。検証データを使うことでモデルが過学習していないか見ることができる。もしテストデータを持っている場合、それをモデルの最適化に使わないように注意すること。
- モデルのハイパラメータを検証データでチューニングする。モデルの汎化性能を最大にするハイパラを探索する。
- アンサンブル: コンペティションなど、とにかく精度が出したいという場合、複数のモデルを合成し、ロバスト性を高める方法が使われる。(分析的な視点では説明性に関して難しさが出るのであまりやったことはない...)
プロジェクト構成
機械学習プロジェクトを進める時のディレクトリ構成など。
KDTの構成
KDT p.267より、ディレクトリではなくファイル内のクラス構成
- model: 各モデルのインターフェイスを統一し、学習や推論ができるwrapperを作る。
- runner: 学習からモデルの保存、クロスバリデーションまで一連の流れを行う。
- utility: ファイルの入出力とログの出力。
AAMLPの構成
AAMLP p.78より
project/
├── input/
│ ├── train.csv
│ └── test.csv
├── src/
│ ├── create_folds.py
│ ├── train.py
│ ├── inference.py
│ ├── models.py
│ ├── config.py
│ └── model_dispatcher.py
├── models/
│ ├── model_rf.bin
│ └── model_et.bin
├── notebooks/
│ ├── exploration.ipynb
│ └── check_data.ipynb
├── LICENSE.txt
└── README.md
その他の例として、テンプレート構築utility "Cookiecutter"やcvpaperchallengeの提案するテンプレートなどがある。
cookiecutter data scienceの構成
project
├── LICENSE
├── Makefile <- Makefile with commands like `make data` or `make train`
├── README.md <- The top-level README for developers using this project.
├── data
│ ├── external <- Data from third party sources.
│ ├── interim <- Intermediate data that has been transformed.
│ ├── processed <- The final, canonical data sets for modeling.
│ └── raw <- The original, immutable data dump.
│
├── docs <- A default Sphinx project; see sphinx-doc.org for details
│
├── models <- Trained and serialized models, model predictions, or model summaries
│
├── notebooks <- Jupyter notebooks. Naming convention is a number (for ordering),
│ the creator's initials, and a short `-` delimited description, e.g.
│ `1.0-jqp-initial-data-exploration`.
│
├── references <- Data dictionaries, manuals, and all other explanatory materials.
│
├── reports <- Generated analysis as HTML, PDF, LaTeX, etc.
│ └── figures <- Generated graphics and figures to be used in reporting
│
├── requirements.txt <- The requirements file for reproducing the analysis environment, e.g.
│ generated with `pip freeze > requirements.txt`
│
├── setup.py <- makes project pip installable (pip install -e .) so src can be imported
├── src <- Source code for use in this project.
│ ├── __init__.py <- Makes src a Python module
│ │
│ ├── data <- Scripts to download or generate data
│ │ └── make_dataset.py
│ │
│ ├── features <- Scripts to turn raw data into features for modeling
│ │ └── build_features.py
│ │
│ ├── models <- Scripts to train models and then use trained models to make
│ │ │ predictions
│ │ ├── predict_model.py
│ │ └── train_model.py
│ │
│ └── visualization <- Scripts to create exploratory and results oriented visualizations
│ └── visualize.py
│
└── tox.ini <- tox file with settings for running tox; see tox.readthedocs.io
以上の例を読んで、自分がいつも使っているディレクトリ構成を見直してみた。いつもDockerで環境構築しているので、Dockerfileは必須。
workspace/
├── dataset
│ ├── working/ # 色々弄る用
│ ├── final/ # 最終結果に利用するデータ
│ └── original/ # オリジナルのデータ
├── references/ # データやモデルに関するマニュアル
├── reports/ # TeXやpdfなどのレポート
│ └── figures/
├── src/
│ ├── __init__.py
│ ├── data/
│ │ └── make_dataset.py # データセットのダウンロード、ディレクトリ整形
│ ├── features/
│ │ ├── build_features.py # データ本体の整形
│ │ └── dataloader.py # datamoduleの定義
│ ├── visualization/
│ │ └── visualize.py
│ ├── train.py
│ ├── inference.py
│ ├── model.py # MMdetなどではconfigsディレクトリにまとめがち
│ └── config.py
├── checkpoint/ # pthやckptのバイナリ
├── train_log/ # Lighting系の学習ログ
├── notebooks/
│ ├── exploration.ipynb
│ └── check_data.ipynb
├── Dockerfile
├── requirements.txt
├── LICENSE.txt
└── README.md
DockerについてはAAMLP 12章でも推奨されており、サービスのデプロイ方法としてFlaskを使った流れも示されている。
以下の記事では「とにかく実験環境を1クリックで作りたい」という場合の最小構成を書いている。
Cross Validation
作成したモデルのデータセットへのfit度合いを測るため、学習データから検証データを切り出す。しかしデータセットは全部有意義に使いたいので、検証データの切り出し方を工夫することで、モデルのロバストネスをうまく測る方法が知られている。
- hold-out validation: 学習データから検証データを切り出す、最も単純な方法。ランダムにシャッフルしてから行う方が良い。与えられたデータが十分大きいならば、cross validationと殆ど変わらない性能評価ができる。
- k-fold: 学習に使えるデータをk等分し、1つを検証データとして扱う。各分割に対して検証を行い、結果の指標を平均して評価することで学習データの損失無く使うことができる。ただし1度の評価にモデルの学習回数がk回必要になるので、必要な時間リソースは増える。
- stratified k-fold: 分割時、含まれるクラス数を均一にする(層化)することで、不均衡データを扱う時でも評価指標の分散を抑えられる。
- group k-fold: 分割時、予めデータが持つグループ属性をもとに分割する。
- leave-one-out cross validation(LOO): データがごく少数の時、1件ずつk-foldをやる。
実務上、データに同じ対象を複数枚撮影したものが含まれている場合があり、そのときは分割にgroup k-foldを使う必要がある。例えば、腫瘍の内視鏡画像を扱う時に、同じ患者のデータが異なるfoldに存在すると、正しい正診率がでないため、患者識別名でグループ化してfoldを作ることが必要になる。
また、学習データと検証データは好きに使っていいが、テストデータは最後の結果を見るのみに使うこと。そうでないと汎化性能を見誤る評価をしてしまうことになる。
以下ではirisデータセットを例に、sklearnのKFoldの使い方と、k-foldを用いないデータの分割を作成する。
dataset = pl.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/datasets/iris.csv")
x = dataset.select(["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"])
y = dataset.select("Species")
from sklearn.model_selection import KFold, StratifiedKFold, GroupKFold, LeaveOneGroupOut
K = 10
# k-fold cross validation
kf = KFold(n_splits=K, shuffle=True)
kf_generator = kf.split(x, y)
for idx_train, idx_test in kf_generator:
x_train, x_test, y_train, y_test = x[idx_train], x[idx_test], y[idx_train], y[idx_test]
from sklearn.model_selection import train_test_split
# hold-out (stratify)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/K, shuffle=True, stratify=y)
理論的には、hold-outよりk-foldの方が期待誤差の不確実性が小さくなるので汎化バインドの意味で優れているらしい。このスライドがわかりやすい。
こちらの記事は分割について非常に詳しく載っている。
時系列データ
hold-outでは予測する時刻の近くのデータを持ってくる。(分布が近いから)
時系列データのクロスバリデーションは適当に分割するだけでは良くないので、学習データの分割に対して別のアプローチを行う。
- 時刻毎に大まかに[1,2,3,4]の分割を作った場合、train[1] val[2], train[1,2] val[3], train[1,2,3] val[4]というふうに漸化的に検証データと学習データを取ることがある。また、長さを合わせるためにtrain[1] val[2], train[2] val[3], train[3] val[4]という区切りもあり得る。この分割はデータの性質をよく見て行う。
周期性やトレンドなどについても考える必要がある。この部分については統計学をちゃんとやった方がいいかもしれない。
バリデーションのテクニック
バリデーションはモデルの改善指標となるスコアを出すことと、テストデータのスコアの分散の見積もりのために必要。より良いバリデーションのためには、テストデータの分割の特徴や分布を真似るように検証データを作る。KDT 5.4では具体的な時系列データでの分割について記されていてわかりやすかった。
テストデータの分布が明らかに異なる場合、以下の対策がある。
- 学習データとテストデータの傾向の違いについて、データ作成の過程について考えたり、EDAを基に考える。
- モデルのバイアスでテストデータにfitするようにする。
Adversarial Validation: 学習データかテストデータかを判別する分類モデルを組み、このスコアを使う。たとえば、特徴量エンジニアリングによって、分類モデルのスコアを低くする(=分布の違いを緩和する)特徴量を作れれば、テストデータに対しても性能が上がる。
クロスバリデーションを信頼せよ: Kaggleの名言(?)。KaggleのようなコンペティションではLeaderboardでのスコアの上下が学習データとテストデータの性質を語ることがあるので、これを指標としてバリデーションの設計の良し悪しを考えることができる。KDT 4.5.5はコンペティション特化のテクニックが詳しく載っていた。
その他のテクニックや考慮事項。
- バリデーションの試行回数がかさみすぎて検証データに過学習することがあるので、乱数シードを変えたりして検証データの分割を変更する。
- 数値データのdata augmentaitonを行う。たとえば最新のデータと分布が異なる過去の分布をいいぐあいに混ぜたり、データを逆に削ったりすることで良くする。
- テストデータに対する予測値を目的変数として学習データに加える。画像系のコンペでたまにあるらしい。
評価指標
複数クラス分類
分類ではAcc, Precision, Recall, F1が一般的に使われる。
- Precision(適合率): TP/(TP+FP), 単純なaccでは計測できない「偽陽性(FP)をどれだけ生んでしまったか」を参照し、スコアから割り引く。これにより、適当に全部陽性にするようなモデルを判別できる。
- Recall(再現率): TP/(TP+FN), 単純なaccでは計測できない「偽陰性(FN)をどれだけ産んでしまったか」を参照し、スコアから割り引く。これにより、検出できなかった陽性が少ないモデルの評価を高められる。感度(sensitivity)、TPR(True Positive Rate)ともいう。
- F1: precisionとrecallの調和平均。
複数クラスを持つデータセットでは、それぞれの指標の計算方法に派生がある。
- Macro Average Precision: 全クラスのPrecisionを個別に計算して、平均する。(おすすめ)
- Weighted Precision: Macro Average Precisionの加重平均版、一般化。
- Micro Average Precision: クラス毎にTPとFPを算出し、その値で全体のPrecisionを計算する。(不均衡データだとあんまりうまく評価できない)
PrecisionだけでなくRecallやF1も同じ方法で計算できる。Micro F1スコアはAccと等価になる。
筆者は非均衡データをよく使うので、Macro F1スコアをAccの代わりに見ることが多い。
TPRの反対として、TNR(True Negative Rate)があり、FP/(TN+FP)として計算される。特異度ともいう。
FPRに対するTPRをプロットした曲線をROC曲線(Receiver Operating Characteristic Curve)と言い、面積をAUC(Area Under the ROC Curve)として評価する。AUCが1に近いほど完璧に分類できているモデルとなる。
AUCの解釈としては「正例と負例をランダムに選んだ時、正例の予測値が負例の予測値より大きい確率」とも言える。この解釈を式にすることで、どの程度予測を改善すればどの程度AUCが上がるかについて直感的に考えることができる。(次の式、
AUCは各行の予測値の大小関係のみに依存するため、各モデルの予測値をアンサンブルする場合でも「予測確率を順位に変換した平均が使われることもある」(←?)。また、不均衡データを扱う際、正例の予測値をどれだけ高確率側に寄せられるかがAUCに大きく影響する(つまり負例の予測値の誤差の影響は小さい)。
以下ではsklearnのAcc, Precision, Recall, F1モジュールを使う例と、confusion matrix(混同行列)を見る例を示す。
target = [1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4]
y_pred = [1, 1, 2, 3, 2, 2, 2, 4, 3, 1, 3, 3, 4, 2, 4, 4, 1]
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score
# average = macro/micro/weighted
# zero_division = 1 or np.nan
score = precision_score(target, y_pred, average="weighted", zero_division=1)
print(score) # 0.7382352941176471
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
fpr, tpr, thresholds = roc_curve(target, y_pred, pos_label=1)
score = auc(fpr, tpr)
print(score) # 0.06666666666666665
from sklearn.metrics import confusion_matrix
cmx = confusion_matrix(target, y_pred)
sns.heatmap(cmx, annot=True)
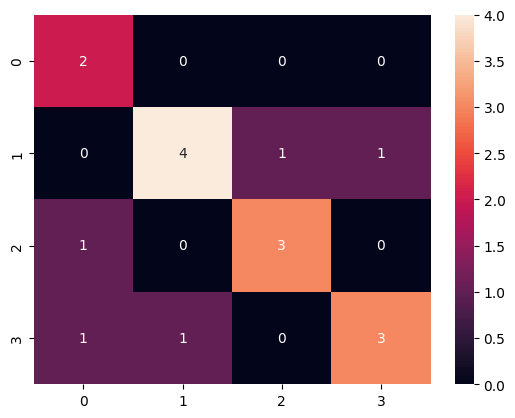
metricsのAPI集
複数ラベル分類
ラベルが1つだけでない、つまりターゲットが複数の値を取ることがある。例えば以下のDTDデータセットなどではテクスチャクラスが複数重複しているデータが存在する。
この時、通常のAcc, Precision, Recall, F1ではなく、Multi-Label Classificationタスク用の指標を用いる。
- Precision@k(P@K): 予測のconfidence上位k個のうち、正解と合致した割合。
- Average Precision@k(AP@K): AP@3 = (P@1 + P@2 + P@3)/3
- Mean Average Precision@k(mAP@k): 全てのサンプルについてAP@kを計算し、その平均を評価指標とする。
レコメンデーションタスクなどでも使用される。
回帰
RMSE(root mean sqrt error)は非常にポピュラー。統計的には誤差が正規分布に従う(=ガウスノイズ)時、最小値が最尤推定量になる。理論面についてはPRMLなどを読むといい。
この
パーセンテージ誤差として、0~1に正規化したものも解釈しやすさから使われている。
決定係数
AAMLPでは他にも重み付きκ係数(Quadratic Weighted Kappa; QWK, Cohen's kappa)や、マシューズ相関係数(Matthews Crrelation Coefficient; MCC)なども紹介されている。KDTの方に説明が書いてあったが、AAMLPの方は触れられただけで、どちらも詳しい理論や数値間などはあまり載ってなかった。
QWKの式を見てみる。QWKは完全な予測で1.0、完全なランダムで0.0の値を取る。
-
O_{i,j} i j i,j -
E_{i,j} i,j i j -
w_{i,j}
簡単に言い表すと次のようになる。
- 重み付きκ係数は同じ対象に対して2つの評価間の一致度を表す場合に用いられる統計量で、評価者間の一致度や繰り返し測定の一致度を見るときに評価方法の信頼性や妥当性を調べられる。クラス間に順序関係がある場合
- マシューズ相関係数は正負が不均衡なデータでの2値分類モデルの精度の評価にはマシューズ相関係数を使用するケースが多い。
以下では紹介されている指標をsklearnから使う例を示す。
from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error, r2_score
target = [1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 4]
y_pred = [1, 1, 2, 3, 2, 2, 2, 4, 3, 1, 3, 3, 4, 2, 4, 4, 1]
metrics = mean_squared_error(target, y_pred)
print(metrics) # 1.294
metrics = mean_absolute_percentage_error(target, y_pred)
print(metrics) # 0.200
metrics = r2_score(target, y_pred)
print(metrics) # -0.2550
変数選択
特徴量が多いと次元の呪いを受けることになるので、いらない特徴量は捨てたい。
- 分散が0に近いデータは一定であり、殆どモデルに影響を及ぼさない。
- 相関係数を使い、相関が高いデータの一方を削除する。
単変量特徴量選択
単変量特徴量選択(univariate feature selection)では、与えられた目的変数、つまり回帰対象の情報から各特徴量を評価する。
- 相互情報量(Mutual information): 変数間の相互情報量がどの程度あるか測る。
- 分散分析(ANOVA F-test): 各特徴量と目的変数間との差があるかどうかを、検定で測る。
- χ^2検定: 非負の各特徴量と目的変数の独立性があるかどうかを、検定で測る。
統計的検定(?)を変数選択に使うのは悪手だと風の噂で聞いた気がするのだが、どの場合に良くてどの場合にわるいのかについて詳しく書いてある資料を探している。AAMLPの書き方では、全てをまとめたutilityになっていてどの手法がどれになっているかコードを読むしかなかったのが惜しい。
dataset = pl.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/datasets/iris.csv")
x = dataset.select(["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"])
y = dataset.select("Species")
from sklearn.feature_selection import SelectKBest # 上位k個の特徴量を保持
from sklearn.feature_selection import SelectPercentile # 上位k%の特徴量を保持
# 分散が小さいものを消す
from sklearn.feature_selection import VarianceThreshold
ver_thresh = VarianceThreshold(threshold=0.1)
x_transformed = ver_thresh.fit_transform(x)
print(x_transformed)
# χ2乗検定で独立性の高い特徴量を消す
from sklearn.feature_selection import chi2
x_selected = SelectKBest(chi2, k=3).fit_transform(x, y)
print(x_selected.shape)
# F検定で分散が等しいものを消す
# Univariate linear regression/classification tests returning F-statistic and p-values.
from sklearn.feature_selection import f_classif, f_regression
f_statistic, p_values = f_classif(x, y)
print(f_statistic.shape, p_values.shape)
x_selected = SelectKBest(f_classif, k=3).fit_transform(x, y)
print(x_selected.shape)
# 相互情報量で、相互に情報の無いものを消す
# Estimate mutual information for a continuous target variable.
from sklearn.feature_selection import mutual_info_classif, mutual_info_regression
mi = mutual_info_classif(x, y)
print(mi.shape)
x_selected = SelectKBest(mutual_info_classif, k=3).fit_transform(x, y)
print(x_selected.shape)
私が行うことがあるのは、説明性が不必要なタスクにおいて、特徴量の次元が大きすぎる時、PCA(主成分分析)やCCA(正準相関分析)などを使うことがある。が、個人的には計算量が問題にならない限り、変数選択は行う必要もない気がしている。KDT 6.2にも、GBDT系ではあまり変数選択は重要ではないと書いてあるので、流し読みした。
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/10, shuffle=True, stratify=y)
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cross_decomposition import CCA
# PCAのために標準化して座標を0に合わせる
scaler = StandardScaler()
x_train_normal = scaler.fit_transform(x_train)
x_test_normal = scaler.transform(x_train)
# PCAで分散最大の軸にargsortする
pca = PCA()
x_train_pca = pca.fit_transform(x_train_normal)
x_test_pca = pca.transform(x_test_normal)
print(pca.explained_variance_) # [2.915 0.939 0.154 0.021]
print(pca.explained_variance_ratio_) # [0.723 0.233 0.038 0.005]
つまり、irisのデータは3つの特徴量で99.5%説明性が保たれることがわかる。
モデル側の変数選択
縮小推定などの文脈でLassoなどは馴染み深いが、より原始的な方法もある。
- 貪欲的変数選択(greedy feature selection): モデルへの各入力特徴量のfit具合(AUC)から、有用な特徴量を判定する。しかし、特徴量の列数に比例してモデル学習回数が増えるので、時間を食う。また、適切に使用しないと過学習を起こす。
- 再帰的特徴量削減(recursive feature elimination): 最初に全部の特徴量を学習させることから始めて、モデルの持つ係数など「特徴量の重要度」を表現する値を使い、各反復で重要度が低いものを捨てていく。
sklearn.feature_selection.RFEで簡単に利用可能。
GBDT
木ベースの手法によるモデルを見ていく。GBDTは欠損値をそのまま使えて、簡単に精度がでるのでよく使われる。特徴量の標準化なども必要なく、カテゴリ変数のone-hot化する必要もない。疎行列(scipy.sparse.csr_matrixやscipy.sparse.csc_matrixなど)への対応もなされているライブラリも多い。
コンペでも、初手GBDT、次にNNやGLM、多様性のためにランダムフォレストやRGF/FFMなどを使う。
GBDTはそれ自体が木手法のアンサンブルモデル。いくつかの定番ライブラリがある。
- xgboost: デフォルトのgbtreeから始めて、線形モデルのgblinear、正則化(DARTアルゴリズム)を使ったdartなど使える。
- lightgbm: xgboostに影響を受けた、高速GBDT。
- catboost: カテゴリ変数にいい感じな扱いを加えたもの。
以下ではxgboostを使った例。
dataset = pl.read_csv("https://vincentarelbundock.github.io/Rdatasets/csv/datasets/iris.csv")
x = dataset.select(["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width"])
y = dataset.select("Species").to_numpy()
y = np.where(y == "setosa", 0, y) # 分類ターゲットはint型にする
y = np.where(y == "versicolor", 1, y)
y = np.where(y == "virginica", 2, y)
y = np.squeeze(y)
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=1/4, shuffle=True, stratify=y)
# GBDTで分類
from xgboost import XGBClassifier
bst = XGBClassifier(n_estimators=2, max_depth=4, learning_rate=1, objective="binary:logistic")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
y_test = np.array(y_test, dtype=np.int64) # dtypeをintで統一しないとエラーになる
y_pred = np.array(y_pred, dtype=np.int64)
from sklearn.metrics import confusion_matrix
cmx = confusion_matrix(y_test, y_pred)
sns.heatmap(cmx, annot=True)
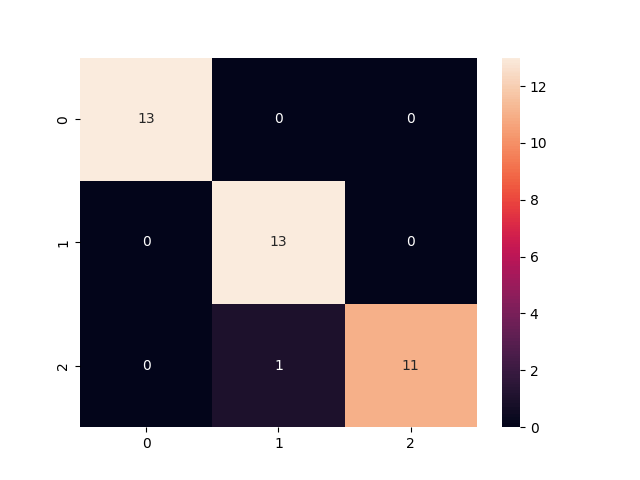
適当に良い精度がでた。
チュートリアルはこれ
モデル作成後の最適化
Hyparameter Tunining
AAMLPには古典的な手法がいくつか載っているが、実用上は以下2点が多い気がする。
- 事前知識から範囲設定してその領域でグリッドサーチする。
- optunaなどにより事前知識を事前分布として与えてベイズ最適化する。
モデルに入っているハイパラは、例えば正則化項のλなどモデルの複雑さを司るパラメータや、ライブラリ上の標準化するかどうかなどの論理値がある。これらをoptunaなどで探索し、良いスコアを出したハイパラを採用する。
このとき全てのパラメータを弄っていると時間がなくなるので、重要なものから変更していくことも検討する。また、検証データを変更することでハイパラによる評価の上下なのかデータの持つ分布への過学習なのか見分けられる。
特にGBDTについてはmax_depthが最も効くハイパラメータで、subsample、colsample_bytree、min_child_weightも重要度が高いと言われているらしい。
ベイズ的な単純な手法についての縮小やモデル比較(理論重視)については以下。
以下はoptunaを使ったモデルの最適化の例。
import optuna
# 目的関数(損失)を最小化する
def objective(trial):
# 事前分布からドロー
n_estimators = trial.suggest_int("n_estimators", 1, 8)
max_depth = trial.suggest_int("max_depth", 1, 8)
lr = trial.suggest_float("learning_rate", 0.01, 3.0)
bst = XGBClassifier(n_estimators=n_estimators, max_depth=max_depth, learning_rate=lr, objective="binary:logistic")
bst.fit(x_train, y_train)
y_pred = bst.predict(x_test)
y_pred = np.array(y_pred, dtype=np.int64)
return 1 - f1_score(y_test, y_pred, average="macro")
study = optuna.create_study()
study.optimize(objective, n_trials=56)
print(study.best_params)
[I 2024-02-06 16:50:44,602] A new study created in memory with name: no-name-3f3a1b2a-1810-4f0c-8429-5490a8b36541
[I 2024-02-06 16:50:44,607] Trial 0 finished with value: 0.053333333333333344 and parameters: {'n_estimators': 5, 'max_depth': 1, 'learning_rate': 0.5902985774721373}. Best is trial 0 with value: 0.053333333333333344.
[I 2024-02-06 16:50:44,614] Trial 1 finished with value: 0.026709401709401615 and parameters: {'n_estimators': 8, 'max_depth': 2, 'learning_rate': 0.7916653380267379}. Best is trial 1 with value: 0.026709401709401615.
...
[I 2024-02-06 16:50:45,150] Trial 55 finished with value: 0.04001600640256109 and parameters: {'n_estimators': 8, 'max_depth': 3, 'learning_rate': 0.8668805677210295}. Best is trial 1 with value: 0.026709401709401615.
{'n_estimators': 8, 'max_depth': 2, 'learning_rate': 0.7916653380267379}
ハイパラーメータが最適化された。
チュートリアルはこれ
評価指標の最適化
与えられた評価指標に対して良い性能を出すモデルを作るため、評価指標に対して最適化された予測値を出力するようにする。
- 閾値の最適化: Nelder-Mead、COBYLA、SLSQPなどの目標関数最適化を使い、正例と負例を識別する閾値を作る。例えばAccであれば0.5を閾値として分類結果を仕分けできるが、F1スコアなどを使う時はこの値の閾値を求めなければならない。
- F1スコアの最適化にはあまり関係ないが、学習データ全体のターゲットと予測値を使って閾値選択を行うと、テストデータに対して最適かどうかわからない。このような場合out-of-foldな方法を取るべき。out-of-fold方法は、例えばk-foldのクロスバリデーションにおいて、ある分割の新たな特徴量を予測変数から作るときに、自身のfoldは使わずに学習したモデルの予測値を加えることで、自身に対する情報が入っていないモデルによる予測値が得られる、よいうようなこと。
このような評価指標最適化を行うことで行うことで、Balanced Acc, mean-F1, QWKなどを使ったモデルの評価を、より高い価値を出すようにできる。
以下はKDT 2.5.3のプログラムの改造版。
from scipy.optimize import minimize
from sklearn.model_selection import KFold
from sklearn.metrics import f1_score
rand = np.random.RandomState(seed=71)
target_prob = np.linspace(0.0, 1.0, 10000)
target = np.array(rand.uniform(0.0, 1.0, target_prob.size) < target_prob)
y_pred = np.clip(target_prob * np.exp(rand.standard_normal(target_prob.shape)* 0.3), 0.0, 1.0)
target # [False False False ... True True True]
y_pred # [0.00e+00 1.10e-04 2.29e-04 ... 9.054e-01 5.25e-01 8.81e-01]
# 最適化の目標関数(カリー化版)
def f1_opt(tr_target, tr_pred):
def f1_opt(x):
return -f1_score(tr_target, tr_pred >= x)
return f1_opt
# クロスバリデーションで閾値を決める
thresholds, tr_score_list, va_score_list = [], [], []
kf = KFold(n_splits=4, random_state=71, shuffle=True)
for i, (tr_idx, va_idx) in enumerate(kf.split(target)):
tr_pred, va_pred = y_pred[tr_idx], y_pred[va_idx]
tr_target, va_target = target[tr_idx], target[va_idx]
# 学習データで閾値を最適化し、検証データで評価する
objf = f1_opt(tr_target, tr_pred)
result = minimize(objf, x0=np.array([0.5]), method="Nelder-Mead")
threshold = result["x"].item()
tr_score = f1_score(tr_target, tr_pred >= threshold)
va_score = f1_score(va_target, va_pred >= threshold)
print(threshold, tr_score, va_score)
thresholds.append(threshold)
tr_score_list.append(tr_score)
va_score_list.append(va_score)
print("test threshold = ", np.mean(thresholds))
threshold tr_score va_score
0.34257812499999984 0.7559183673469387 0.7570422535211268
0.34277343749999983 0.7598457403295548 0.7450980392156863
0.31787109374999983 0.7548253676470589 0.7584803256445047
0.3234374999999998 0.7545569184913448 0.7588603196664351
test threshold = 0.33166503906249983
モデル合成
- Ansembling(アンサンブル): 異なるモデルを組み合わせて性能を上げる。
- モデル平均: モデルの精度を見ながら適当に決めたり、スコアを目標関数にして最適化するなどして加重平均を取る。
- スタッキング: モデル合成を効率的に組み合わせる方法。テストデータの分布がかなり厳密に学習データと同じ場合、スタッキングにより学習データを使い尽くすことで精度が高まる。しかし時系列のようなiidが仮定できないデータの場合はあまり良くならない。
スタッキングは簡単に表せば「あるモデルに対して、foldごとに予測値を新たな特徴量としてデータに加えることで、複数モデルを使った予測値を新たな学習データに加えるアンサンブル方法」だと思った(もしかしたら間違ってるかも)。SklearnStackingなどに詳しく書いてあった。
モデル合成の理論に関してはPRML 14章が詳しく書いてある。
感想
機械学習について「講義で触ったことがある」という人にとっては非常に良い本だと思う。一般的、常識的な手法や機械学習プロジェクトの推進方法などについて網羅的に載っているので、全体の雰囲気を掴みながら写経で挙動を確認できるため、変に止まらず学習を進めることができると感じた。
一方、ある程度研究などで論文や実装や触ったことがある人にとっては、ページ数に対して得るものは少ない可能性もある。特にAAMLPは昔の深層学習を扱った章が多くを占めており、現在の手法を触る上ではあまり参考にしないほうがいい部分もあった。また、網羅的である良さの裏として(対象読者を考えれば当然だが)各々の手法に対する理論的な裏付けなどは全く書かれていないので、理論屋や原理がわからないと腑に落ちないという人からすると不十分な内容になっている。NN系の手法については、モデルの構成などではなく「インターネットでの最新手法の探し方」について言及してくれればよかったかもしれない。
個別の感想として、KDTは題名通りKaggleのための本という内容で、データ分析汎用な話題というよりKaggleにおいての考え方がフィーチャーされていたと感じた。章立ては自然で、データ分析関連を始めたい人はKDT 1.5.1から読み始めればスムーズに読めると思う。数値データとGBDT重点で書かれていることもあり、AAMLPより理論面や実際のシチュエーションが深堀りされており、得られるものが多かったと感じた。AAMLPは、全体の構成として技術的なセクションの分け方で、最初の章からスムーズに読めて良かった。惜しい点としては、本の構成として1/4ほどがNN系の話題になっている点と、各章で示されるキーワードごとのプログラム例ではなく、全体をまとめたutilityが載っている点が挙げられる。画像分類はNN系の話題のみだったため(個人的には)あまり得られる知識がなかったが、自然言語処理に関しては古典的手法についてかなり言及があり、網羅性の観点では良いと感じた。プログラム例もできれば小分けにして最小構成で記載したほうが対象読者層も読みやすいのではないかと感じた。
総合的に、学校の講義でデータ分析について触ったことはあるという人に勧めるならば、まずKDTの方を読むことをおすすめする。その後各手法の理論面が知りたくなったらPRML2巻を読むのが良いと思う。画像や自然言語処理に関しては、古典的な方法を定番書でさらってから、NN系手法についてarxivに上がっているサーベイを読む方が良い。
前処理と特徴量エンジニアリングについては、近い内に復習してまとめたい。
Discussion