【Juliaで因果推論】回帰分析 - OLS推定量の不偏性・効率性・一致性

• 3つの"良い"推定方法の基準: 不偏性・効率性・一致性 (一致性が一番大事)
• 仮定 $E[U|X]=0$ が満たされていれば，OLS推定は不偏性をもつ (平均的に真の値と等しい: $E[\hat{\beta}] = \beta$)
• 真の値$\beta$に対して2つの不偏推定量$\hat{\beta}, \tilde{\beta}$があるとすると，$Var[\hat{\beta}] < Var[\tilde{\beta}]$のとき，推定量$\hat{\beta}$は$\tilde{\beta}$よりも効率的である．
• 仮定 $Cov[X, U]=0$ が満たされていれば，OLS推定は一致性をもつ (サンプルサイズを無限大に増やせば真の値と等しい: $\hat{\beta} \xrightarrow{p} \beta$)

---

前回はOLS推定の結果が因果効果として信用に値するようなものとなるために必要な仮定 $E[U|X]=0$ (zero conditional mean assumption)を紹介しました．ザックリ言えば「$X$と$U$に相関はない」となります^[1]．この仮定が満たされないとOLS推定は適切な結果を与えません．そもそも，"適切な"推定の基準とは何でしょうか？推定量(estimator)$\hat{\beta}$は，母集団における関係性の係数パラメータ・真の値(estimand)$\beta$を推定するものです．よって$\hat{\beta}$と$\beta$がどれくらい違うかが"推定量の良さ"の基準となります^[2]．ここでは計量経済学の3つ"推定量の良さ"の基準を考えます．推定量の不偏性(unbiasedness) ，効率性(efficiency) ，一致性(consistency) です.

不偏性 (unbiasedness)

私たちが知りたいのは母集団で成り立つ関係式(population model)$Y = \beta_0 + \beta_1 X + U$のパラメータ$\beta_1$です．そこで真の値$\beta_1$を推定をするために，母集団から$\{(X_i, Y_i): i=1, 2, \dots, N\}$をランダムサンプリングします．推定量は確率変数である$X, Y$の関数なので，推定量自体も確率変数であり，分布が考えられます．"良い"推定量の分布とはどんな分布でしょうか？まず思いつくのは「推定量の分布の期待値が真の値と等しい」ことです．実際は1度しかサンプルできなくても，その1回きりの推定が平均的には真の値と等しいのであれば，推定結果は信用できそうってことです．

不偏推定量の定義

母集団のパラメータ $\theta$ の推定量 $W$について，

$$E[W] = \theta$$

であれば，$W$は$\theta$の不偏推定量(unbiased estimator)である^[3]．

不偏性は推定量の期待値に関する特性です．つまり，「もし複数回サンプリングできたとして，それぞれ推定した場合，推定量は平均的に真の値を当てる」ということです．実際の分析ではサンプリングは1回の場合がほとんどなので推定は1回きりです．推定量に不偏性があれば，1回きりの分析も"平均的には"真の値を当てていることになります^[4]．

推定量が不偏性を持たないとき，推定量の期待値と真の値は異なります．その違いをバイアス(bias)といいます．

推定量のバイアスの定義

$$\text{Bias}(W) = E[W] - \theta$$

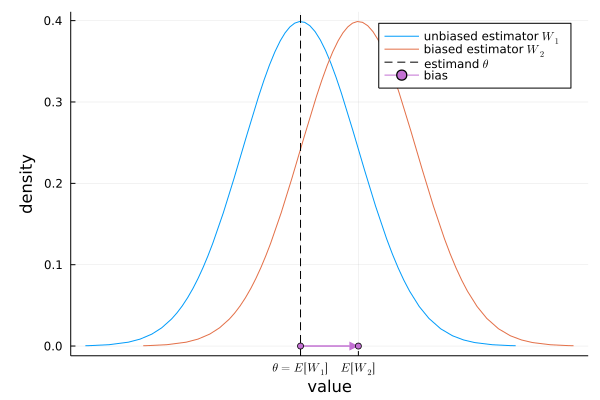
Figure.1 推定量の分布(不偏性，バイアス)のイメージ

Figure.1は真の値$\theta$を推定する2つの仮想的な推定量$W_1, W_2$の分布を表しています．$W_1$の分布の期待値$E[W_1]$は$\theta$と一致するので不偏推定量です．一方$W_2$の分布の期待値$E[W_2]$は$\theta$と異なり，バイアスしています．

ところで，真の値を推定するものであればどんなものでも推定量です．極論，でたらめな乱数randn()を推定量とすることもできますが，乱数は不偏性を持ちません．一方，OLS推定は「仮定$E[U|X]=0$さえ満たせば」不偏性を持ちます．まずは式で確認しましょう.

OLS推定の不偏性

---

仮定$E[U|X]=0$が成り立てば，OLS推定量$\hat{\beta}_1$は不偏推定量である．

Proof:

母集団における$Y, X, U$の関係が$Y = \beta_0 + \beta_1 X + U$であり，母集団から$\{(X_i, Y_i): i=1, 2, \dots, N\}$をランダムサンプリングしたとします^[5]．

母集団の関係式とランダムサンプリングより，

$$Y_i = \beta_0 + \beta_1 X_i + U_i, \quad i=1, 2, \dots, N$$

真の値$\beta_1$との違いを示したいので，まずはOLS推定量 $\hat{\beta}_1$を$\beta_1$を含んだ式に変形していきます．

$$\begin{align*} \hat{\beta}_1 & = \frac{\sum_{i=1}^N (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^N (X_i - \bar{X})^2} \\ & = \frac{\sum_{i=1}^N (X_i - \bar{X})Y_i}{\sum_{i=1}^N (X_i - \bar{X})^2} \\ & = \frac{\sum_{i=1}^N (X_i - \bar{X})(\beta_0 + \beta_1 X_i + U_i)}{\sum_{i=1}^N (X_i - \bar{X})^2} \end{align*}$$

2行目は和のオペレーターの特性，3行目はpopulation modelを使って変形しています．分子に注目すると，

$$\begin{align*} \sum_{i=1}^N (X_i - \bar{X})(\beta_0 + \beta_1 X_i + U_i) &= \beta_0 \sum_{i=1}^N (X_i - \bar{X}) + \beta_1 \sum_{i=1}^N (X_i - \bar{X}) X_i + \sum_{i=1}^N (X_i - \bar{X})U_i \\ & = 0 + \beta_1 \sum_{i=1}^N (X_i - \bar{X})^2 + \sum_{i=1}^N (X_i - \bar{X})U_i \\ \end{align*}$$

従って，OLS推定量$\hat{\beta}_1$は，

$$\begin{align*} \hat{\beta}_1 & = \frac{\beta_1 \sum_{i=1}^N (X_i - \bar{X})^2 + \sum_{i=1}^N (X_i - \bar{X})U_i}{\sum_{i=1}^N (X_i - \bar{X})^2} \\ & = \beta_1 + \frac{\sum_{i=1}^N (X_i - \bar{X})U_i}{\sum_{i=1}^N (X_i - \bar{X})^2} \end{align*}$$

と表せます．これは$\hat{\beta}_1$と$\beta_1$の関係を表しています^[6]．

$\hat{\beta}_1$が不偏性を持つかどうかは($\{X_1, \dots, X_N\}$^[7]に関する条件付)期待値を確認します．

$$\begin{align*} E[\hat{\beta}_1|X_1, \dots, X_N] & = \beta_1 + E \left[ \frac{\sum_{i=1}^N (X_i - \bar{X})U_i}{\sum_{i=1}^N (X_i - \bar{X})^2} \mid X_1, \dots, X_N \right] \\ & = \beta_1 + \frac{\sum_{i=1}^N (X_i - \bar{X}) E \left[ U_i \mid X_1, \dots, X_N \right] }{\sum_{i=1}^N (X_i - \bar{X})^2} \end{align*}$$

ここで，zero conditional mean assumption $E[U|X]=0$ が成り立つとすると，それぞれの$Ui$に対して，

$$E[U_i | X_i] = 0, \quad i = 1, \dots, N$$

さらに，zero conditional mean assumption $E[U|X]=0$は母集団における確率変数$X$と$U$の関係についての仮定なので，ユニット同士に関係がないランダムサンプリングであれば，ユニット内だけでなくユニット間でも成り立ちます.

$$E[U_i | X_1, \dots, X_i , \dots, X_N] = 0, \quad i = 1, \dots, N$$

従って$\hat{\beta}_1$の条件付期待値は以下のようになります．

$$\begin{align*} E[\hat{\beta}_1|X_1, \dots, X_N] & = \beta_1 + \frac{\sum_{i=1}^N (X_i - \bar{X}) 0 }{\sum_{i=1}^N (X_i - \bar{X})^2} \\ & = \beta_1 \end{align*}$$

最後に繰り返し期待値の法則より，見た目を不偏性の定義に寄せると，

$$\begin{align*} E[\hat{\beta}_1] & = E[E[\hat{\beta}_1|X_1, \dots, X_N]] \\ & = \beta_1 \end{align*}$$

となり，仮定$E[U|X]=0$が成り立ていれば^[8]OLS推定量$\hat{\beta}_1$は不偏性を持つことが分かります^[9]．

---

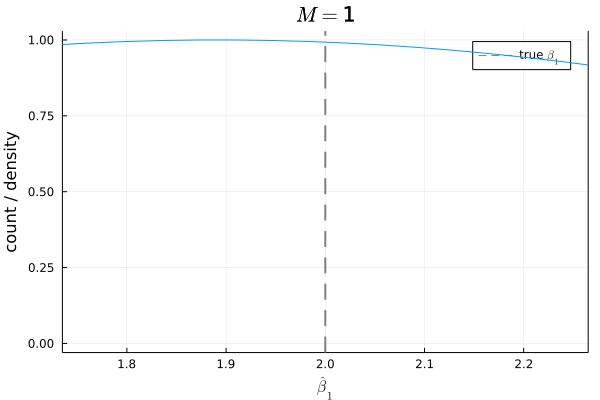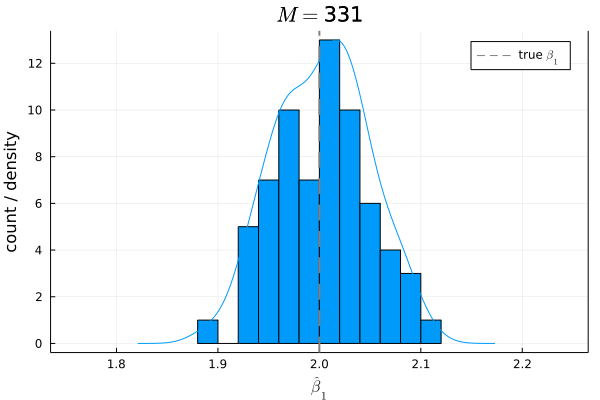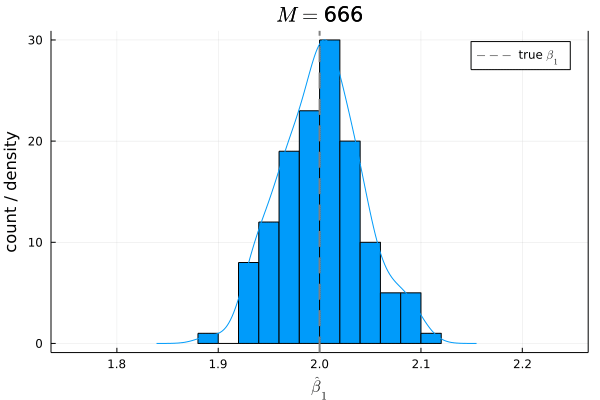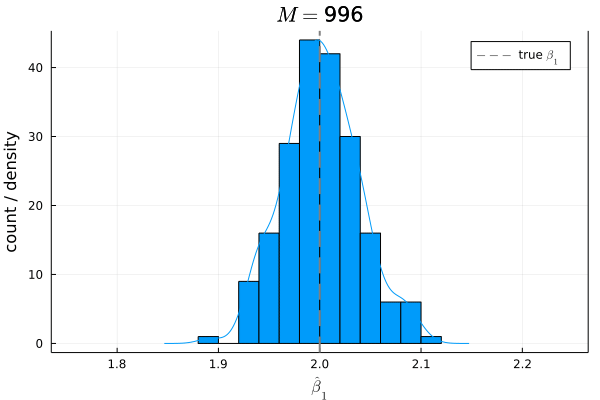
目で見るとわかりやすいので，シミュレーションしてみましょう^[10]．母集団から複数回，$M$回サンプリングできたとして，それぞれサンプルごとに推定した結果$\hat{\beta}_1^{(1)}, \dots, \hat{\beta}_1^{(M)}$の平均(推定量の分布の期待値)が真の値($\beta_1$)と等しいかどうか確認します．

シミュレーションでは$X$と$Y$の母集団における真の関係を以下のようなpopulation modelとします．

$$Y = 1 + 2 X + U$$

$X$の$Y$への因果効果の真の値は$\beta_1 = 2$です．

さて，まずは仮定$E[U|X]=0$を満たしている場合を見てみましょう．ここで注意すべきこととして，仮定$E[U|X]=0$は$E[U]=0$を仮定していますが，誤差項$U$がどんな分布に従うかについては何も仮定してません．つまり，$U$の平均が$0$であればどんな分布でも大丈夫です^[11]．仮定$E[U|X]=0$を満たすように，$X$と$U$は独立に生成します．具体的には以下のような例を考えましょう．

仮定$E[U|X]=0$を満たしたOLS推定の不偏性のシミュレーション:

• サンプルサイズ: $N = 200$
• 母集団モデル: $Y = 1 + 2 X + U$
• $X$の生成プロセス: $X \sim \mathcal{N}(3, 1)$ (どんな分布でもOK)
• $U$の生成プロセス: $U \sim \mathcal{U}[-1, 1]$ ($E[U]=0$であればどんな分布でもOK)
• $X$と$U$の生成は独立 ($E[U|X]=0$)
• サンプル数: $M = 1000$

using Random, Plots, StatsPlots, Distributions, DataFrames, GLM, LaTeXStrings, Printf

# Generate simulated data (zero conditional mean)

β1 = 2 # true params
β0 = 1
N = 200 # sample size

function gen_data_zcm()
    
    X = rand(Normal(3, 1), N) # X (no distribution ristrictions)
    # X = rand(Uniform(1, 3), N) # you can change to any distribution
    U = rand(Uniform(-1, 1), N) # U (the only ristriction is E[U]=0)
    # U = rand(Chi(1)-1, N) # you can change to any distribution
    # scatter(X, U) # E[U|X]=0, X and U are independent (no correlation)
    Y = β0 .+ β1 * X + U # linear population model
    df = DataFrame(Y = Y, X = X)
    return df
end


# Estimate with different sample multiple times
Random.seed!(1234)
M = 1_000 # number of sample
β1_hats = []

# plot with cool GIF animation
anim = @animate for m in 1:5:M
    df = gen_data_zcm()
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])

    histogram(β1_hats, bins=10, xlims=[1.75, 2.25], title=L"M="*@sprintf("%d", m), xlabel=L"\hat{\beta}_1", ylabel="count", label=false)
    density!(twinx(), β1_hats, xlims=[1.75, 2.25], xticks=false, yticks=false, label=false)
    vline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta_1")
    title!(L"M = " * @sprintf("%d", m))
end
gif(anim, "sim_unbiasedness.gif", fps=60)

# Bias
mean(β1_hats) - β1
# 0.0072132362380079584

$M=1000$回サンプリングしてそれぞれ推定すると，推定値$\hat{\beta}_1$の平均は真の因果効果$\beta_1$とほぼ等しくなります．つまり，仮定$E[U|X]=0$を満たせばOLS推定量は不偏性をもつことが分かります．

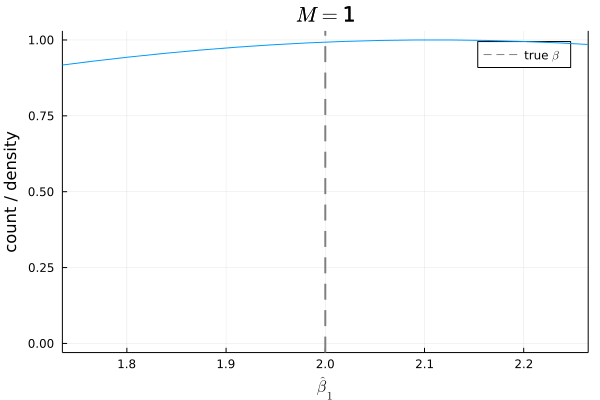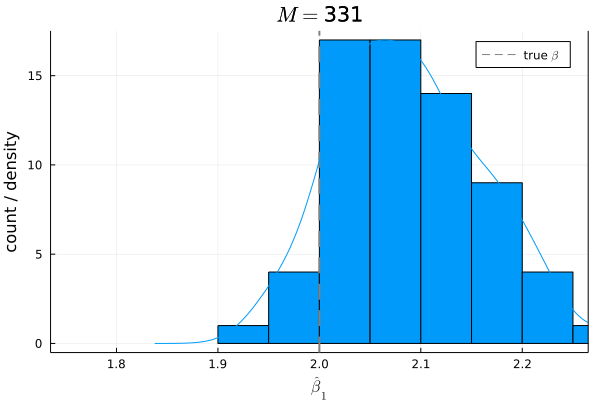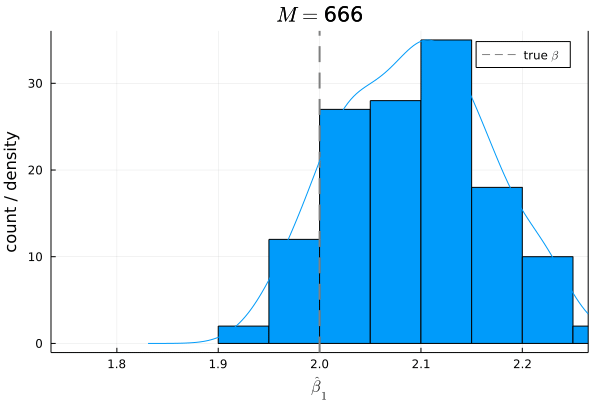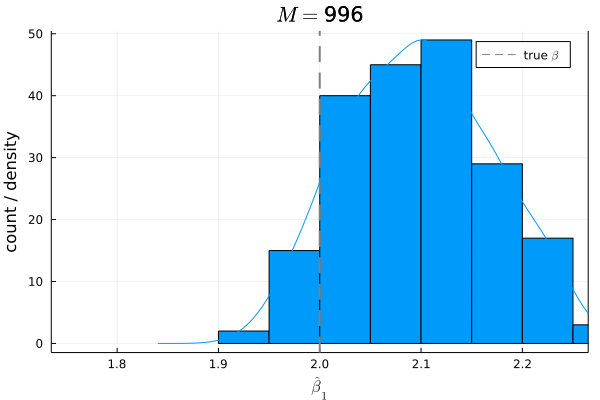
今度は，仮定$E[U|X]=0$を満たさない場合にOLS推定量は不偏性を持たないことをシミュレーションで確かめましょう^[12]．

仮定$E[U|X]=0$を満たさないOLS推定のバイアスのシミュレーション:

• サンプルサイズ: $N = 200$
• 母集団モデル: $Y = 1 + 2 X + U$
• $X$の生成プロセス: $X \sim \mathcal{N}(3, 1)$ (どんな分布でもOK)
• $U$の生成プロセス: $U \sim \mathcal{N}(0, 1)$ ($E[U]=0$であればどんな分布でもOK)
• $X$と$U$の相関あり ($Cov[X, U]\neq0, E[U|X]\neq0$)
• サンプル数: $M = 1000$

using Random, Plots, StatsPlots, Distributions, DataFrames, GLM, LaTeXStrings, Printf

# Generate simulated data (not zero conditional mean)

β1 = 2 # true params
β0 = 1
N = 200 # sample size

function gen_data_notzcm()
    XU = rand(MvNormal([3, 0], [1 0.1; 0.1 1]), N) # Correlated Multivariate Normal Corr[X, U] = 0.1
    X = XU[1, :]
    U = XU[2, :]
    # scatter(X, U) # E[U|X]!=0, X and U are orrelated
    Y = β0 .+ β1 * X + U # linear population model
    df = DataFrame(Y = Y, X = X)
    return df
end


# Estimate with different sample multiple times
Random.seed!(1234)
M = 1_000 # number of sample
β1_hats = []

# plot with cool GIF animation
anim = @animate for m in 1:5:M
    df = gen_data_notzcm()
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])

    histogram(β1_hats, bins=10, xlims=[1.75, 2.25], title=L"M="*@sprintf("%d", m), xlabel=L"\hat{\beta}_1", ylabel="count", label=false)
    density!(twinx(), β1_hats, xlims=[1.75, 2.25], xticks=false, yticks=false, label=false)
    vline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta")
    title!(L"M = " * @sprintf("%d", m))
end
gif(anim, "sim_biased.gif", fps=60)

# Bias
mean(β1_hats) - β1
# 0.09866853535852238

バイアスは，$X$と$U$の相関が大きいほど大きくなります^[13]．また，$X$と$U$が正に相関していればOLS推定量は真の因果効果よりも過大に評価(上にバイアス)し，負に相関していれば真の因果効果よりも過小に評価(下にバイアス)します．

シミュレーションの結果からもわかる通り，もし仮定 $E[U|X]=0$ が成り立たなければ，OLS推定量は不偏性を持ちません．$X$と$U$に相関があるとOLS推定量はバイアスします．この場合，「分析結果は平均的に外している」ことになります．たまたま分析に使ったサンプルが奇跡的にバイアスのない結果を与える可能性もありますが，確認しようがないので普通は信用できないものとなります．

効率性 (efficiency)

推定量が不偏性をもっていても，サンプルによって得られる推定値にばらつきが生じてしまいます．このばらつき具合は推定量の分布の分散(sampling variance)として考えられます．ばらつきが小さい推定量ほど良い推定量であり，効率的であるといいます．

相対的効率性の定義

母集団のパラメータ$\theta$の不偏推定量$W_1, W_2$について，

$$Var[W_1] \leq Var[W_2]$$

のとき，$W_1$は$W_2$よりも相対的に効率的である．

効率性は推定量の分散に関する特性です．また，効率性はあくまでも複数の不偏推定量の相対的な分散の大きさの違いによって議論されます．

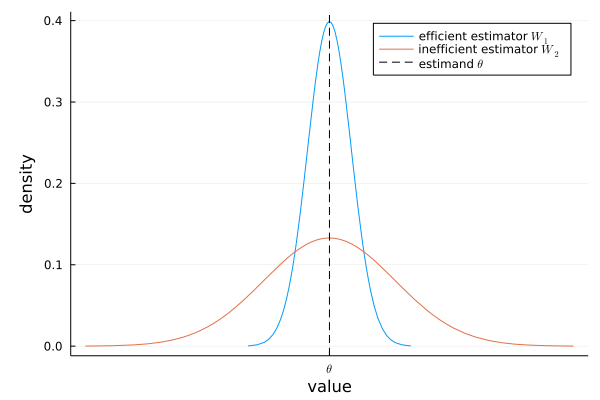
Figure.2 推定量の分散・効率性のイメージ

Figure.2より，推定量の分散が大きいと，推定によって結果のばらつきが大きくなります．すると同じ分析をしても大きく結果が異なる傾向が強くなってしまいます．よって当たり前ですが推定量の($X$についての条件付)分散は小さいほうが良いです．

不偏性や後で紹介する一致性は推定の結果が真の値とどれだけ異なるのかについてですが，効率性は真の値とどれだけ離れるかではなくどれだけ推定にばらつきがあるかについてです．なので不偏性や一致性と比べると効率性はあまり重要視されないことが多いです．しかし，もし不偏性と一致性の両方を持つような推定方法が複数ある場合は，より(推定のばらつきが少ない)効率的な推定方法が良いでしょう．ちなみに，推定量の分散$Var[\beta | X_1, \dots X_N]$自体は仮説検定で必要不可欠です．推定量の分散の計算は仮説検定で紹介します^[14]．

一致性 (consistency)

推定量が不偏性を持っていたとしても推定量の分散によって，推定にばらつきが生じてしまいます．中にはそもそも不偏性を持たないような推定量もあります^[15]．これでは多くの推定が信用できないものとなってしまいます．そこで，新たに漸近的な(asymptotic, large sample properties)議論を導入します．ザックリ言うと「サンプルサイズが無限大であれば推定量は真の値と一致するかどうか」です．サンプルサイズが無限大のとき真の値と一致すれば，推定量は一致性を持つといいます．通常，計量経済学では一致性を推定量の最低条件としています．それくらい重要な特性です．

一致推定量の定義

母集団のパラメータ $\theta$ のサイズ$N$のサンプルに基づく推定量を$W_N$とし，推定量の数列$\{W_1, \dots W_N\}$^[16]を考える．任意の$\epsilon > 0$に対して$N \rightarrow \infty$のとき，

$$P(|W_N - \theta| > \epsilon) \rightarrow 0$$

と確率収束すれば，$W_N$は$\theta$の一致推定量(consistent estimator)である．また，このとき$W_N$の確率極限(probability limit)は真の値$\theta$はと一致する．

$$\text{plim}(W_N) = \theta$$

一致性は推定量の確率極限に関する特性です．定義を直訳すれば，「サンプルサイズを無限大にすれば，推定量$W_N$が$\theta$と異なる確率はゼロ」となります．つまり，「もしサンプルサイズを無限大だったら，推定量は真の値をドンピシャ(確率1)で当てる」ということです．逆にデータを無限大に使っても真の値を当てないような推定量は，不偏性があっても効率的であってもポンコツだということです^[17]．

推定量の漸近バイアスの定義

漸近バイアス(asymptotic bias)^[18]とは，推定量が一致性を持たない(inconsistent)ときの，推定量の確率極限$\text{plim}(W_N)$と真の値$\theta$の差のことです．

$$\text{Asymptotic bias}(W_N) = \text{plim}(W_N) - \theta$$

推定量$W_N$が一致性を持たないとき，推定量の確率極限は真の値と一致しない($\text{plim}(W_N) \neq \theta$)ので，推定量は漸近バイアスします．つまり，サンプルサイズが無限大のときに必ず真の値と異なる推定結果が出てきます^[19]．従って，一致性を持たない推定方法は計量経済学では適切でないと判断します．

OLS推定の一致性

OLS推定は，$X$と$U$に相関がない^[20]なら一致性を持ちます．

---

$Cov[X,U]=0$が成り立てば，OLS推定量$\hat{\beta}_1$は一致推定量である．

Proof:

母集団における$Y, X, U$の関係が$Y = \beta_0 + \beta_1 X + U$であり，母集団から$\{(X_i, Y_i): i=1, 2, \dots, N\}$をランダムサンプリングしたとします．

OLS推定量の不偏性の証明で導出した，OLS推定量$\hat{\beta}_1$を真の値$\beta_1$で表したところから始めます．

$$\begin{align*} \hat{\beta}_1 & = \beta_1 + \frac{\sum_{i=1}^N (X_i - \bar{X})U_i}{\sum_{i=1}^N (X_i - \bar{X})^2} \\ & = \beta_1 + \frac{\sum_{i=1}^N (X_i - \bar{X})(U_i - \hat{U})}{\sum_{i=1}^N (X_i - \bar{X})^2} \quad \text{和のオペレーターと平均} \\ & = \beta_1 + \frac{\frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})(U_i - \hat{U})}{\frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2} \quad \text{分子分母}N\text{で割る} \end{align*}$$

両辺に$\text{plim}$をとって，確率極限に飛ばします．

$$\begin{align*} \text{plim} \hat{\beta}_1 & = \text{plim} \left( \beta_1 + \frac{\frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})(U_i - \hat{U})}{\frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2} \right) \\ & = \beta_1 + \frac{\text{plim}\left( \frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})(U_i - \hat{U}) \right)}{\text{plim}\left( \frac{1}{N}\sum_{i=1}^N (X_i - \bar{X})^2 \right)} \\ \end{align*}$$

ここで大数の法則を使うと，

$$\begin{align*} \text{plim} \hat{\beta}_1 & = \beta_1 + \frac{Cov[X_i, U]}{Var[X_i]} \\ \end{align*}$$

更に仮定より$Cov[X,U]=0$なので，

$$\begin{align*} \text{plim} \hat{\beta}_1 & = \beta_1 \end{align*}$$

---

よって，$Cov[X,U]=0$が成り立てば，OLS推定量$\hat{\beta}_1$は一致推定量となります^[21]．
もし，$Cov[X, U] = 0$ ($X$と$U$に相関がない) が成り立たなければ，OLS推定量は一致性も持ちません．$X$と$U$に相関がある($Cov[X, U] \neq 0$)とOLS推定量は漸近バイアスします．

$$\begin{align*} \text{plim} \hat{\beta}_1 & = \beta_1 + \frac{Cov[X_i, U]}{Var[X_i]} \\ \text{plim} \hat{\beta}_1 - \beta_1 & = \frac{Cov[X_i, U]}{Var[X_i]} \end{align*}$$

• $Cov[X_i, U] > 0$なら，$\text{plim} \hat{\beta}_1 > \beta_1$となり，OLS推定量は正の方向に漸近バイアス(過大評価)します．
• $Cov[X_i, U] < 0$なら，$\text{plim} \hat{\beta}_1 < \beta_1$となり，OLS推定量は負の方向に漸近バイアス(過小評価)します．

この漸近バイアスの式は，めちゃくちゃ重要です^[22]．$X$と$U$の相関の符号だけでバイアスの方向が分かるようになります．

さて，一致性についてもシミュレーションで理解を深めましょう．サンプルサイズ$N$を少しずつ増やしていき，推定値が真の値と一致するかどうかを見ていきます．

仮定$Cov[X, U] = 0$を満たしたOLS推定の一致性のシミュレーション:

• サンプルサイズ: $N = 1:10000$
• 母集団モデル: $Y = 1 + 2 X + U$
• $X$の生成プロセス: $X \sim \mathcal{N}(5, 2)$ (どんな分布でもOK)
• $U$の生成プロセス: $U \sim \mathcal{U}[-1, 1]$ (どんな分布でもOK)
• $X$と$U$の生成は独立 ($Cov[X, U] = 0$)

using Random, Plots, StatsPlots, Distributions, DataFrames, GLM, LaTeXStrings, Printf

# Generate simulated data (not correlated X and U)

β1 = 2 # true params
β0 = 1

function gen_data_notcorr(N)
    X = rand(Normal(5, 2), N)
    U = rand(Uniform(-1, 1), N)
    Y = β0 .+ β1 * X + U # linear population model
    df = DataFrame(Y = Y, X = X)
    return df
end

# Estimate with increasing sample size
Random.seed!(1234)
N_inf = 300 # infinity sample size
β1_hats = []

# plot with cool GIF animation
anim = @animate for N in 1:N_inf
    df = gen_data_notcorr(N)
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])
    plot(β1_hats, marker=:circle, xlabel=L"N", ylabel=L"\hat{\beta}_1", label="OLS estimator "*L"\hat{\beta}_1"*"with sample size "*L"N")
    hline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta_1=2")
end
gif(anim, "sim_consistency.gif", fps=60)

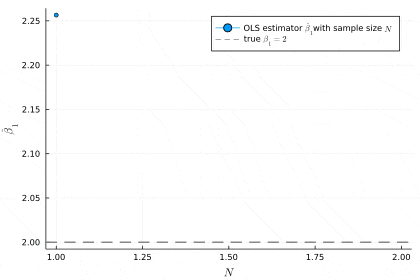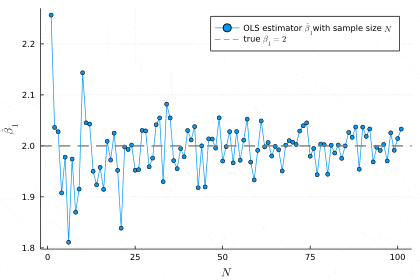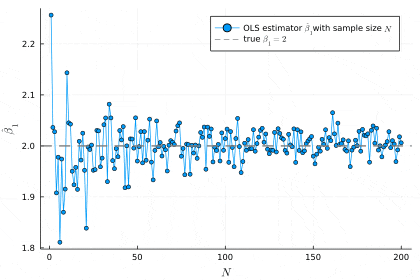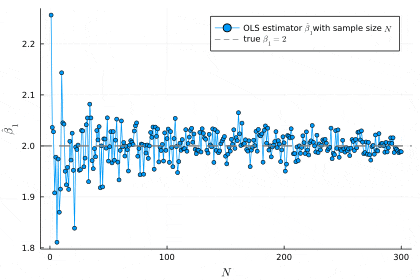
サンプルサイズが増えるにつれ，推定値が真の値の値に近づいていることが分かります．サンプルサイズ$N=300$を無限大とするのはちょっと少ないので，$N=10000$^[23]のときを見てみましょう.

Random.seed!(1234)
N_inf = 10_000 # infinity sample size
β1_hats = []

for N in 1:N_inf
    df = gen_data_notcorr(N)
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])
end

scatter(β1_hats, markersize=2, alpha=0.1, xlabel=L"N", ylabel=L"\hat{\beta}_1", label="OLS estimator "*L"\hat{\beta}_1"*"with sample size "*L"N")
hline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta_1=2")

# the value of OLS estimator at N = 10000
print(β1_hats[N_inf])
# 2.003832883131732

$N=10000$のとき，OLS推定量の推定値はほぼ真の値と等しいことが分かります．重要なのは「サンプルサイズが増えれば増えるほど推定の精度が上がっている」ことです．グラフを見ると，右に行くほど($N$が大きいほど)OLS推定量が真の値に近づいています．このように，いつまでもサンプルサイズを増やしてもずっと推定の精度が上がる余地があるような推定方法が一致推定量です．このシミュレーションでは$Cov[X,U]=0$としているので，$X$と$U$に相関が無ければOLS推定量は一致性を持つことが分かります．

今度は$X$と$U$をわざと相関させて，OLS推定量が漸近バイアスする様子をシミュレーションしましょう．

仮定$Cov[X, U] = 0$を満たさないOLS推定の漸近バイアスのシミュレーション:

• サンプルサイズ: $N = 1:10000$
• 母集団モデル: $Y = 1 + 2 X + U$
• $X$の生成プロセス: $X \sim \mathcal{N}(5, 2)$ (どんな分布でもOK)
• $U$の生成プロセス: $U \sim \mathcal{N}(0, 1)$ (どんな分布でもOK)
• $X$と$U$の相関あり ($Cov[X, U] \neq 0$)

using Random, Plots, StatsPlots, LinearAlgebra, Statistics, DataFrames, GLM, LaTeXStrings, Printf

# Generate simulated data (not correlated X and U)

β1 = 2 # true params
β0 = 1

function gen_data_corr(N)
    Σ = [2 0.9; 0.9 1]
    L = cholesky(Σ).L
    b = [5 0]
    XU = randn(N, 2) * L .+ b # correlated X and U
    X = XU[:, 1]
    U = XU[:, 2]
    Y = β0 .+ β1 * X + U # linear population model
    df = DataFrame(Y = Y, X = X)
    return df
end

# Estimate with increasing sample size
Random.seed!(1234)
N_inf = 300 # infinity sample size
β1_hats = []

# plot with cool GIF animation
anim = @animate for N in 1:N_inf
    df = gen_data_corr(N)
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])
    plot(β1_hats, marker=:circle, xlabel=L"N", ylabel=L"\hat{\beta}_1", label="OLS estimator "*L"\hat{\beta}_1"*"with sample size "*L"N")
    hline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta_1=2")
end
gif(anim, "sim_inconsistency.gif", fps=60)

$X$と$U$が相関していると，OLS推定量は真の値とは異なる値に確率収束していくことが分かります．$N=10000$も見てみましょう．

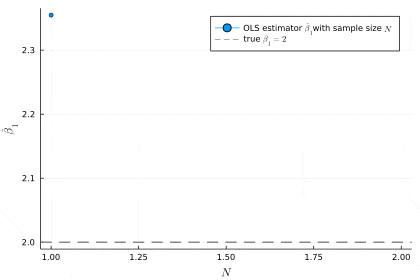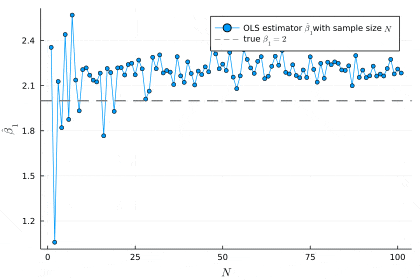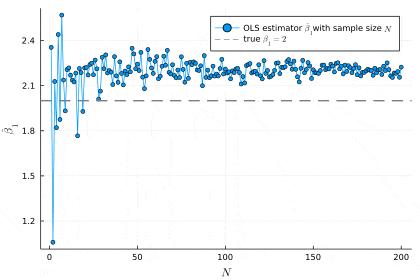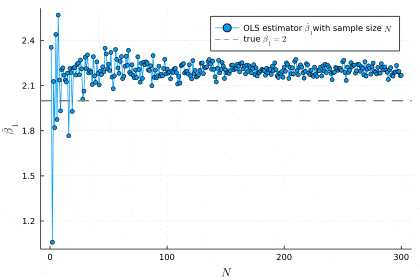
Random.seed!(1234)
N_inf = 10_000 # infinity sample size
β1_hats = []

for N in 1:N_inf
    df = gen_data_corr(N)
    ols = lm(@formula(Y ~ X), df)
    push!(β1_hats, coef(ols)[2])
end

scatter(β1_hats, markersize=2, alpha=0.1, xlabel=L"N", ylabel=L"\hat{\beta}_1", label="OLS estimator "*L"\hat{\beta}_1"*"with sample size "*L"N")
hline!([β1], linestyle=:dash, color=:gray, linewidth=2, label="true "*L"\beta_1=2")

# the value of OLS estimator at N = 10000
print(β1_hats[N_inf])
# 2.1985094056667593

$Cov[X, U]\neq 0$の場合，サンプルサイズが無限大でもOLS推定量はドンピシャで外し，漸近バイアスします．漸近バイアスの仕組みとしては，$X$と$U$の相関の符号によって漸近バイアスの方向が決まり，$X$と$U$の相関の強さによって漸近バイアスの大きさが決まります^[24]．今回の場合は$X$と$U$を正に相関させているのでOLS推定量は真の値よりも過大評価しています．

不偏性がなくても一致性があれば，サンプルサイズが十分大きいとき推定は外れません．一方一致性がないと，どんなにサンプルサイズを大きくしてもOLS推定量は外れます．よって，「一致性を持たないことによる漸近バイアス」は「不偏性を持たないことによるバイアス」よりも深刻な問題として捉えられることが多いです^[25]．

仮定$E[U|X]=0$が成り立たないとOLS推定は不偏性と一致性を持たないので，OLS推定は信用できないものになります．実際に被説明変数$Y$と説明変数$X$だけで回帰分析しようとしても，普通$X$と$U$は相関するので仮定$E[U|X]=0$が満たされることはほとんどありません．このような場合はどうしたらよいか，次回紹介します．

Refference

Cunningham, S., 2021. Causal inference: the mixtape. Yale University Press.
Wooldridge. 2019. Introductory Econometrics: A Modern Approach
Stock, J.H. and Watson, M.W., 2018. Introduction to econometrics 4th Edition. Boston: Addison Wesley.

脚注

1. 必要条件という意味でザックリ表現してます．自分の分析を守るときに「$X$と$U$に相関はない」だけだと自分のOLS推定の結果が適切である理由として不足です($E[U|X]=0$が必要十分)．一方，他者の分析を批判するときに「$X$と$U$に相関がある」は相手のOLS推定の結果が適切でない理由としては十分です．

2. 推定量$\hat{\beta}$は確率変数の式であり，データがあれば数値として推定値が得られます．一方，真の値$\beta$は知らないものです．知ってる$\hat{\beta}$と知らない$\beta$がどれだけ異なるかを考えるのはかなりtoughな推測統計の議論です．

3. 一般的なパラメータと推定量の表記をしていますが，OLSであれば$E[\beta] = \hat{\beta}$です．

4. 逆に言えば，不偏性があっても"平均的には当てる"だけなので，外すときは外します．

5. 特に議論してきませんでしたが，線形回帰の大前提の仮定として，線形のpopulation modelを想定することと母集団からランダムサンプリングすることがあります．詳しくは代表的な計量の教科書を参照してください(Wooldridge, 2019, p.40-41)．

6. この表現は推定量の特性を考えるうえでめちゃくちゃ使います．後ほどOLS推定量の一致性でも出てきます．

7. 推定量はサンプリングしたデータ$i = 1, \dots, N$が手元にあるので，そのデータの情報を既知としたうえでの条件付期待値$E[\hat{\beta}_1|X_1, \dots, X_N]$を吟味します．

8. 誤差項$U$が特定の分布に従う仮定は一切していません．$E[U|X]=0$だけです．「誤差項が正規分布に従う」なんて仮定はしてません．

9. 切片の不偏性$E[\hat{\beta}_0] = \beta_0$についてもOLS推定量の式$\hat{\beta}_0 = \bar{Y} - \hat{\beta}_1 \bar{X}$から簡単に証明できます．

10. 式でごちゃごちゃやっても実感がわきにくい時に，シミュレーションをすると，ビジュアルで理解できて効果的です．

11. 当たり前すぎますが，説明変数$X$に関しては何の仮定も必要ありません．

12. 少し仮定をviolateさせてみるのもシミュレーションの醍醐味です．

13. データ生成プロセスのMvNormal()の分散共分散行列をいじってみてください．

14. そこそこ大変です．

15. 例えば，最尤推定は一致性を持ちますが，不偏性は必ずしも持ちません．

16. 推定量$W$がサンプルサイズ$N$に依存し，サンプルサイズが1増えるごとに新しい推定量をリストに追加していくイメージです．

17. サンプルサイズ無限大というのはあくまでも仮想的な話ですが，その仮想的な話ですら外すような推定量はポンコツです．

18. 実際は漸近バイアスでも単に"バイアス"と呼ぶことが多いです．何なら実証研究における"バイアス"のほとんどは漸近バイアスのことです．

19. 一致性を持たないポンコツ推定量は仮にサンプルサイズが無限大でもドンピシャ(確率1)で外します．

20. 「$X$と$U$に相関がない」は$E[U|X]=0$の必要条件なので，$E[U|X]=0$よりも弱い仮定です．

21. ここでも，誤差項$U$が特定の分布に従う仮定は一切していません．$Cov[X,U]=0$だけです．

22. 欠落変数バイアスそのものです

23. 無限大としてはまだまだ不十分ですが，プロットもあるので勘弁してください．

24. コードをいじってやってみてください

25. サンプルサイズが小さければ，一致性が成り立っていると主張しにくいので，不偏性がないとダメです．一方, サンプルサイズが十分に大きいときは一致性さえあれば不偏性がなくてもエコノミスト的には大丈夫らしいです(Wooldridge, 2019, p.164)．