Juliaで見る漸近理論 (確率変数の数列の収束)
確率収束
確率変数でない数列の収束に引き続き,確率変数の数列の収束について見ていきます.
確率収束の定義
-
任意の
\epsilon > 0 N \rightarrow \infty P(|x_{N} - a | > \epsilon) \rightarrow 0 \{x_N: N=1, 2, \ldots \} a
x_N \xrightarrow{p} a \quad \text{as} \quad N \rightarrow \infty
と書く.このときa
\text{plim } x_N = a
書く. -
特に
a=0 \{ x_N \} \mathcal{o}_p(1)
x_N = \mathcal{o}_p(1)
または
x_N \xrightarrow{p} 0
と書く. -
任意の
\epsilon > 0 N > N_{\epsilon} P(|x_N | \geq b_\epsilon) \leq \epsilon b_\epsilon \leq \infty N_{\epsilon} \{ x_N \}
x_N = \mathcal{O}_p(1)
と書く.
確率収束の漸近記号の定義
-
確率変数でない正の数列を
\{ a_N \} \frac{x_N}{a_N} = \mathcal{o}_p(1) \{ x_N: N=1, 2, \ldots \}
\mathcal{o}_p(a_N)
であるという. -
確率変数でない正の数列を
\{ a_N \} \frac{x_N}{a_N} = \mathcal{O}_p(1) \{ x_N: N=1, 2, \ldots \}
\mathcal{O}_p(a_N)
であるという.
確率変数でない数列
Juliaでプロットして確率収束の感覚をつかめるようにします.
確率収束の例
例:
using Plots, LaTeXStrings, Random
N_inf = 1_000
x(N) = sqrt(N) * rand() # z ~ Univariate(0, 1)
anim = @animate for N in 1:10:N_inf
Random.seed!(1234)
x_N = x.(Vector(1:N))
# check convergence in probability
# scatter x_N.
p1 = scatter(x_N, xlabel=L"N", ylabel=L"x_N \equiv \sqrt{N}z", legend=false, title=L"z \sim Uniform(0, 1)")
# scatter x_N / N^δ
p2 = scatter(x_N ./ Vector(1:N).^(2), xlabel=L"N", ylabel=L"N^{-\delta}x_N", label=L"x_N=\mathcal{o}(N^{2})", legend=:topleft)
scatter!(x_N ./ Vector(1:N).^(1/2), label=L"x_N=\mathcal{O}(N^{1/2})")
scatter!(x_N ./ Vector(1:N).^(1/3), label=latexstring(L"N^{-(1/3)}x_N ", "is unbounded"))
plot(p1, p2, layout=(2, 1))
end
gif(anim, "6_plim_uni.gif", fps=60)
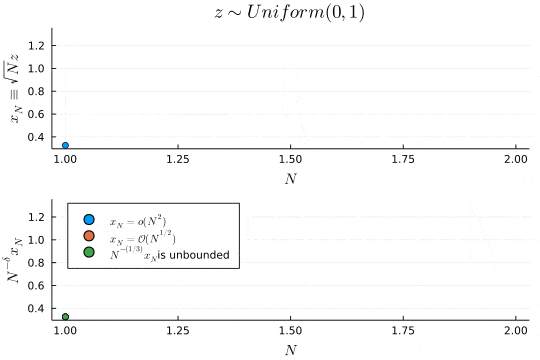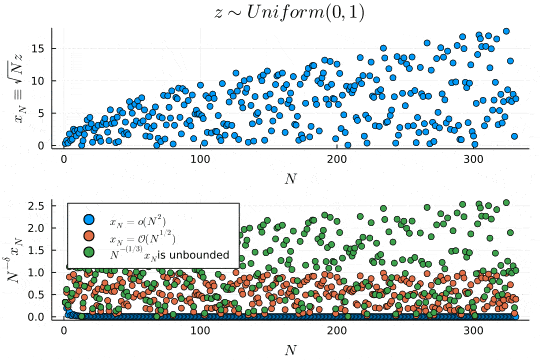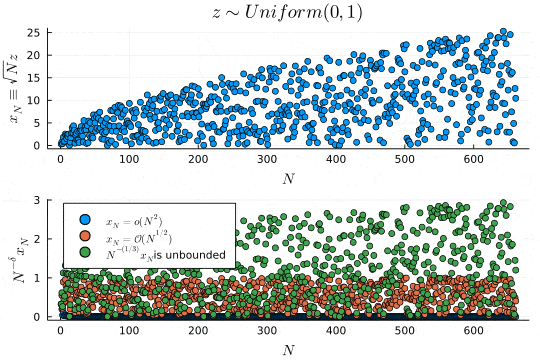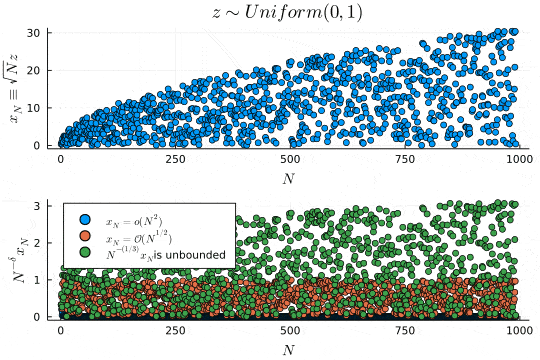
上のプロットは確率変数
なので,
と表すことができます.
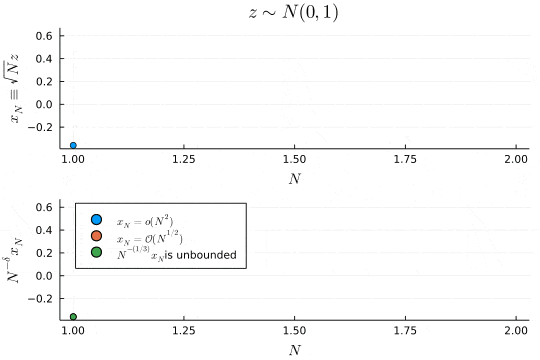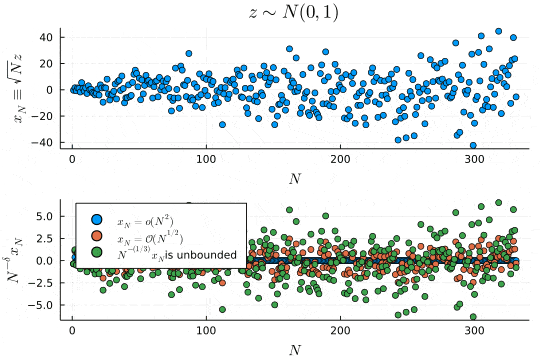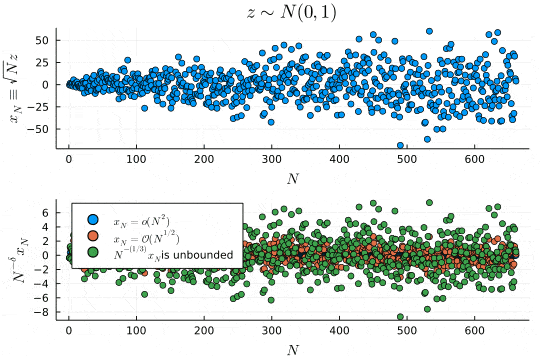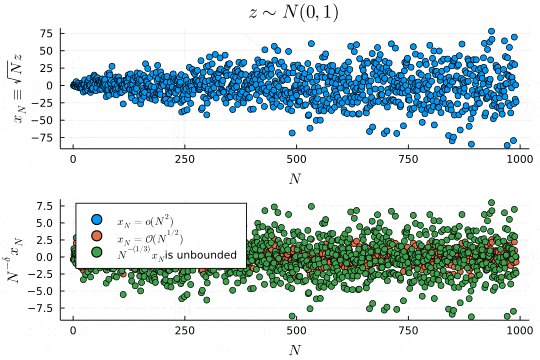
一方
N_inf = 1_000
Random.seed!(1234)
xnorm(N) = sqrt(N) * randn() # z ~ Normal(0, 1)
anim = @animate for N in 1:10:N_inf
# check convergence in probability
Random.seed!(1234)
x_N = xnorm.(Vector(1:N))
# scatter x_N
p1 = scatter(x_N, xlabel=L"N", ylabel=L"x_N \equiv \sqrt{N}z", legend=false, title=L"z \sim N(0, 1)")
# scatter x_N / N^δ
p2 = scatter(x_N ./ Vector(1:N).^(2), xlabel=L"N", ylabel=L"N^{-\delta}x_N", label=L"x_N=\mathcal{o}(N^{2})", legend=:topleft)
scatter!(x_N ./ Vector(1:N).^(1/2), label=L"x_N=\mathcal{O}(N^{1/2})")
scatter!(x_N ./ Vector(1:N).^(1/3), label=latexstring(L"N^{-(1/3)}x_N ", "is unbounded"))
plot(p1, p2, layout=(2, 1))
end
gif(anim, "7_plim_norm.gif", fps=60)
Reference
Wooldridge, J. M. (2010). Econometric analysis of cross section and panel data second edition. MIT press.
Discussion