Juliaで見る漸近理論 (確率変数でない数列の収束)

回帰分析の漸近バイアスについて議論するために必要な漸近理論について確認しておきます．

数列の収束

まずは確率変数ではなく，普通の数列の値の収束を見てみます．

(確率変数でない)数列の収束の定義

• 任意の $\epsilon > 0$ に対して，$N>N_{\epsilon}$ ならば $| a_{N} - a |<\epsilon$ となるような正の整数 $N_{\epsilon}$ が存在するとき，数列$\{ a_N: N=1, 2, \ldots \}$ は実数$a$に 収束する(converge) といい，
  

  $$a_N \rightarrow a \quad \text{as} \quad N \rightarrow \infty$$
  
  と書く．このとき$a$は 極限(limit) という．

• 任意の $\epsilon > 0$ に対して，すべての正の整数 $N=1, 2, \ldots$について$|a_N| \leq b$ となる実数$b < \infty$が存在するとき，数列$\{ a_N: N=1, 2, \ldots \}$ は有界である(bounded) といい，そうでなければ有界でない(unbounded) という．

上記は$\epsilon$-$N$論法による定義です．回帰分析は$N$をサンプルサイズとし，$a_N$は(確率変数ではありませんが)$N$の関数である何らかの推定量として考えるといいでしょう．数列$\{ a_N: N=1, 2, \ldots \}$についてはちょっと謎ですが，サンプルサイズが$\{N=1, N=2, \ldots\}$と増えていったときの，それに対応する推定量の数列 $\{a_1, a_2, \ldots\}$ とイメージすればいいと思います.

収束の定義ではサンプルサイズ$N$が$N_{\epsilon}$よりも大きければ$\{ a_N \}$の収束の誤差を$\epsilon$よりも小さく抑えられるようになっています．つまり，サンプルサイズ$N$が無限大に近づけば，誤差は限りなく$0$に近づき，$a_N$は$a$とほぼ等しくなるということです．

これだけだとなかなか実感が湧きにくいので，いくつか$N$の関数$a_N$を例として用意し，Juliaでプロットして視覚的に表現してみます．

数列の収束:例

例1. $a_N = 2 + \frac{1}{N}$ のとき，$a_N$は2に収束する．$(a_N \rightarrow 2$ as $N \rightarrow \infty)$

using Plots, LaTeXStrings

N_inf = 100 # large sample size

# converged sequence
a1(N) = 2 + 1/N

# plot "a_N = 2 + 1/N"
anim = @animate for N in 1:N_inf
    plot(
	    a1, Vector(1:N), markershape=:circle, label=L"a_N = 2 + \frac{1}{N}",
	    title="Converged Sequence", xlabel=L"N", ylabel=L"a_N",
	    xlim=(0, Inf), ylims=(1.9, 3.1)
    )
end
gif(anim, "1_converged_sequence.gif", fps=60)

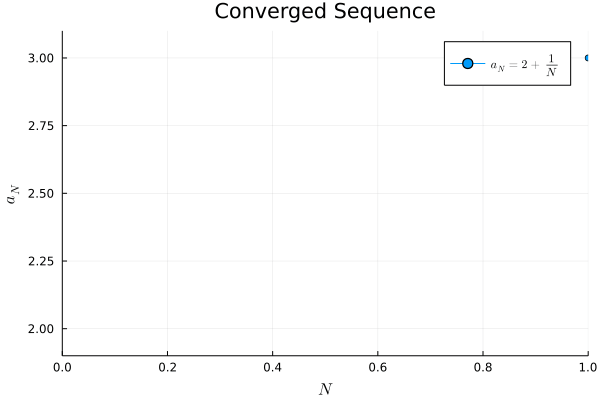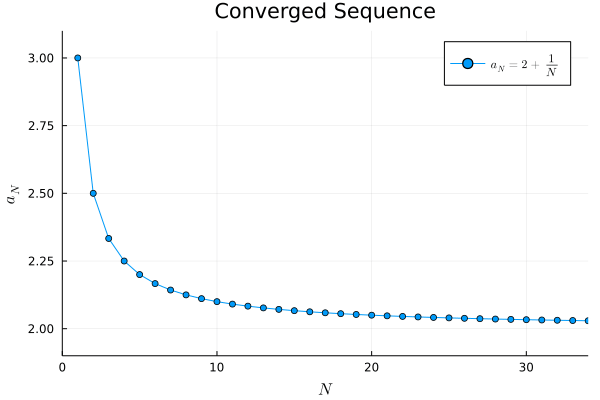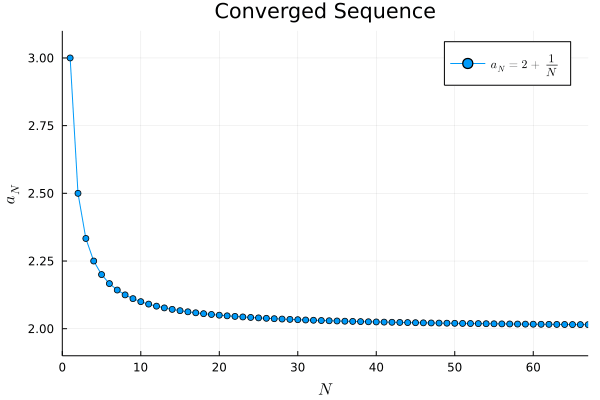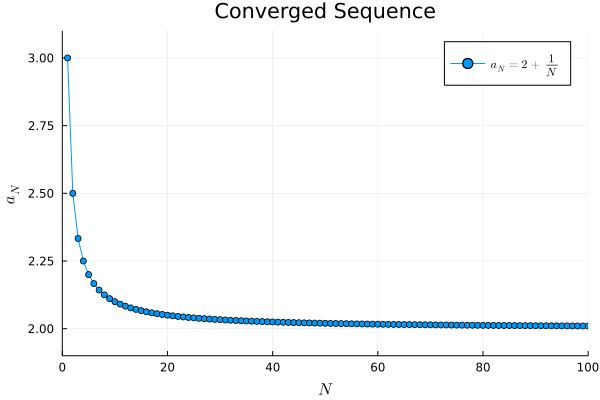
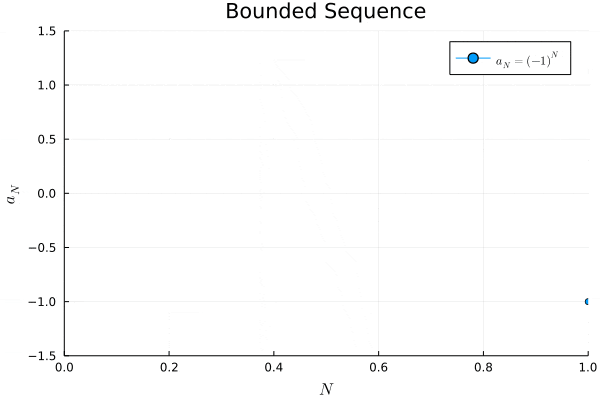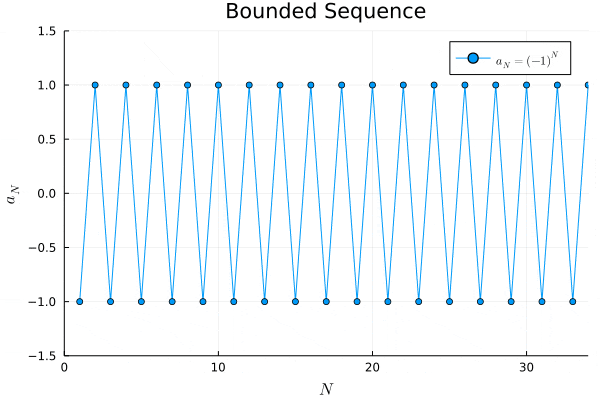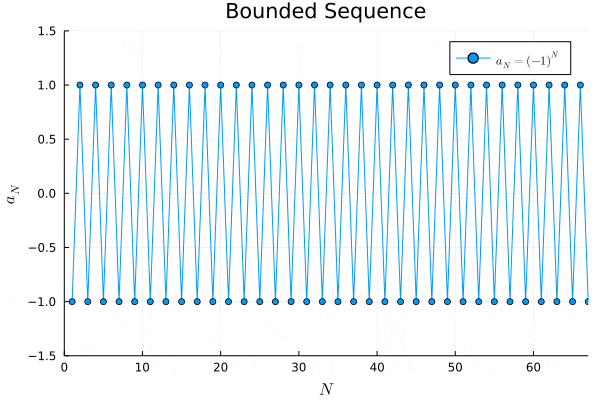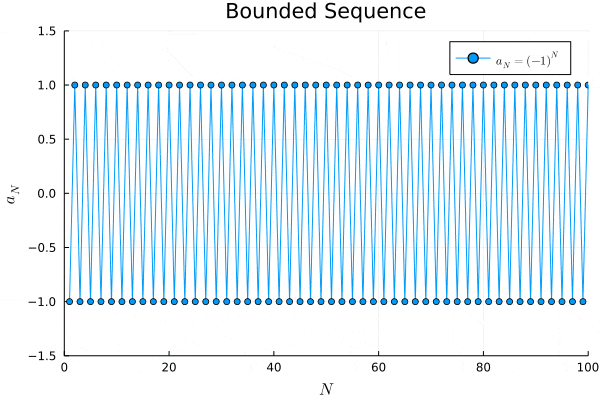
例2. $a_N = (-1)^{N}$ のとき，$a_N$は極限を持たないが有界である．

# bounded sequence
a2(N) = (-1) ^ N

# plot "a_N = (-1) ^ N"
anim = @animate for N in 1:N_inf
    plot(
        a2, Vector(1:N), markershape=:circle, label=L"a_N = (-1)^{N}",
        title="Bounded Sequence", xlabel=L"N", ylabel=L"a_N",
        xlim=(0, Inf), ylims=(-1.5, 1.5)
        )
end
gif(anim, "2_bounded_sequence.gif", fps=60)

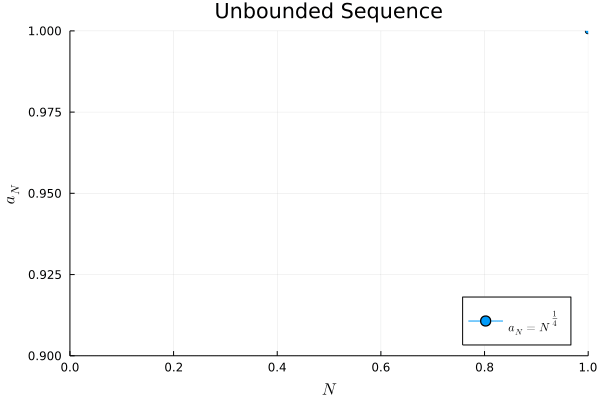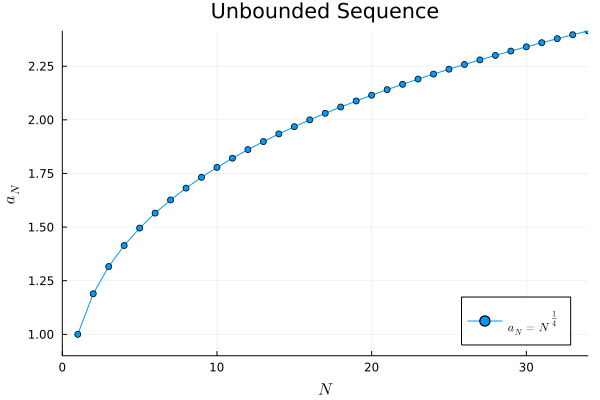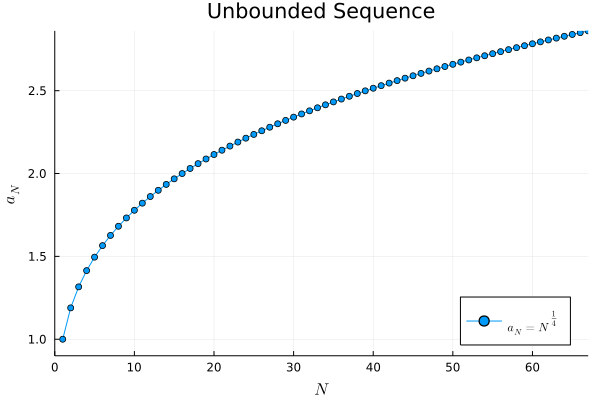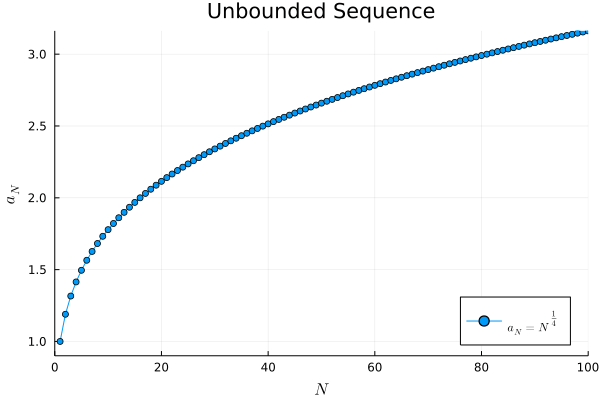
例3. $a_N = N^{\frac{1}{4}}$ のとき，$a_N$は有界ではなく，無限大に発散する．$(a_N \rightarrow \infty$ as $N \rightarrow \infty)$

# unbounded sequence
a3(N) = N ^ (1/4)

# plot "a_N = N ^ (1/4)"
anim = @animate for N in 1:N_inf
    plot(
        a3, Vector(1:N), markershape=:circle, label=L"a_N = N^{\frac{1}{4}}", 
        title="Unbounded Sequence", xlabel=L"N", ylabel=L"a_N",
        xlim=(0, Inf), ylim=ylim=(0.9, Inf), legend=:bottomright
        )
end
gif(anim, "3_unbounded_sequence.gif", fps=60)

漸近記号の定義

ここでは収束・発散の概念を導入します．

• $\frac{a_N}{N^{\lambda}}$が有界であるとき，数列$\{ a_N \}$は$\mathcal{O}(N^{\lambda})$であるといい，
  

  $$a_N = \mathcal{O}(N^{\lambda})$$
  
  と書く．特に$\lambda = 0$のとき，$\{ a_N \}$そのものが有界であり，
  
  $$a_N = \mathcal{O}(1) \quad (N \rightarrow \infty)$$
  
  と書く．

• $\frac{a_N}{N^{\lambda}} \rightarrow 0$であるとき，$\{ a_N \}$は$\mathcal{o}(N^{\lambda})$であるといい，
  

  $$a_N = \mathcal{o}(N^{\lambda})$$
  
  と書く．特に$\lambda = 0$のとき，$\{ a_N \}$そのものが$0$に収束し，
  
  $$a_N = \mathcal{o}(1) \quad (N \rightarrow \infty)$$
  
  と書く．

ランダウ記号(Landau Symbol)$\mathcal{O}(\cdot), \mathcal{o}(\cdot)$は，感覚的には収束・発散の速さを表しています．$a_N = \mathcal{o}(N^{\lambda})$は，$N^{\lambda}$の発散のスピードが$a_N$よりも早く，$N$が無限大に近づくほど$\frac{a_N}{N^{\lambda}}$は$0$に収束することを表します．一方$a_N = \mathcal{O}(N^{\lambda})$は，$N^{\lambda}$と$a_N$の発散のスピードが等しく，$a_N$の発散が$N^{\lambda}$の発散によって押さえられて，$\frac{a_N}{N^{\lambda}}$は有界となることを表します．

ここでも，例としていくつかの$a_N$をプロットしてみます．

漸近記号:例

例4: $a_N = \log(N)$ のとき，任意の$\lambda >0$において，$a_N = \mathcal{o}(N^{\lambda})$

# log(N) / N^λ → 0 (converged) (for any λ>0) as N → ∞ 
# (log(N) は N^λ と比べて高次元の無限小で、早く0に収束する)
# we write log(N) = o(N^λ)

a4(N) = log(N)
Ninvλa4(N, λ) = a4(N) / N^λ
Nλ(N, λ) = N^λ

anim = @animate for N in 1:N_inf
    p1 = plot(Nλ.(Vector(1:N), 3/4), markershape=:circle, label=L"N^{3/4}",title=L"N^\lambda, a_N", xlabel=L"N", ylabel=L"N^\lambda, a_N", ylims=(0, 50))
    plot!(Nλ.(Vector(1:N), 2), markershape=:circle, label=L"N^{2}")
    plot!(Nλ.(Vector(1:N), 5), markershape=:circle, label=L"N^{5}")
    plot!(a4, Vector(1:N), markershape=:circle, label=L"a_N = \log(N)")
    p2 = plot(Ninvλa4.(Vector(1:N), 3/4), markershape=:circle, label=L"a_N /N^{3/4}", title=L"a_N = \mathcal{o}(N^{\lambda})", xlabel=L"N", ylabel=L"N^{-\lambda}a_N")
    plot!(Ninvλa4.(Vector(1:N), 2), markershape=:circle, label=L"a_N / N^2")
    plot!(Ninvλa4.(Vector(1:N), 5), markershape=:circle, label=L"a_N / N^5")    
    plot(p1, p2, layout=(2, 1))
end
gif(anim, "4_landau_log.gif", fps=60)

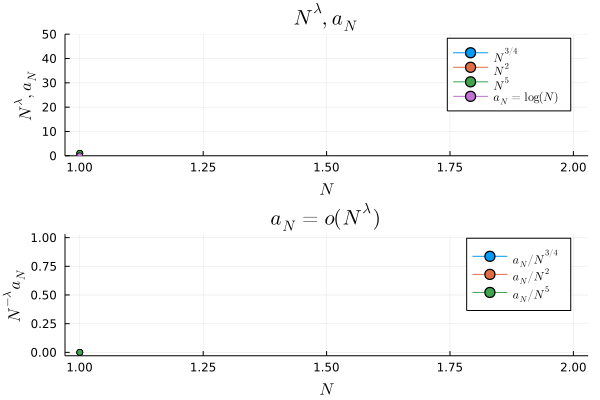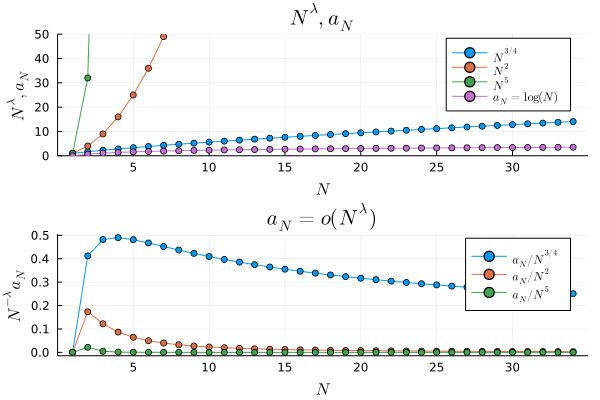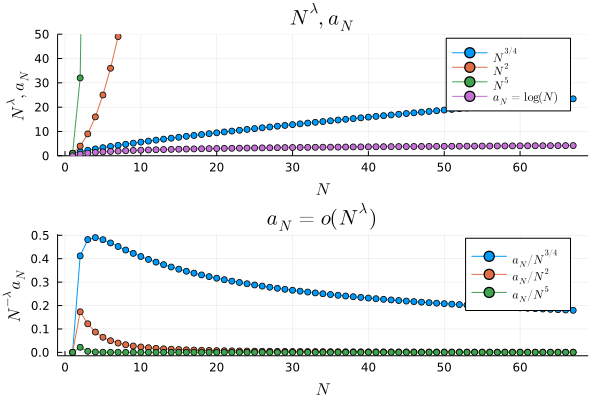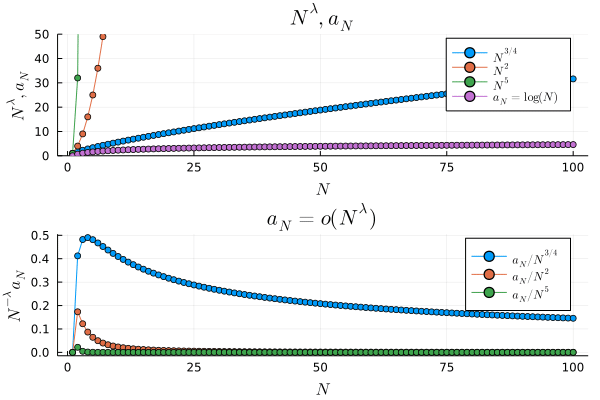
上のプロットを見てみると，$a_N$と$N^\lambda$どちらも$N$が大きくなるにつれ発散していますが，発散のスピードは$a_N$よりも$N^\lambda$の方が速いことが確認できます．この発散のスピードの違いにより$\frac{a_N}{N^\lambda}$が$0$に収束し，その様子が下のプロットで確認できます．「$a_N$よりも$N^\lambda$の方が速く発散し，$\frac{a_N}{N^\lambda}$が$0$収束する」ということをランダウ記号$\mathcal{o}(\cdot)$を用いて表現すれば，

$$a_N = \log(N) = \mathcal{o}(N^{\lambda}), \quad \forall \lambda > 0$$

となります．ちなみに，$\lambda$が大きくなるほど，$N^\lambda$の発散のスピードがさらに速くなるため，$\frac{a_N}{N^\lambda}$の$0$への収束も早くなります．

例5: $a_N = 10 + \sqrt{N}$ のとき，$a_N = \mathcal{O}(N^{\frac{1}{2}})$．また，任意の$\gamma > 0$において，$a_N = \mathcal{o}(N^{\frac{1}{2} + \gamma})$

# (10 + √N) / N^(1/2) is bounded as N → ∞ 
# (10 + √N は N^(1/2) によって押さえられる)
# we write 10 + √N = O(N^(1/2))

# (10 + √N) / N^(1/2 + γ) → 0 (converged) (for any γ>0) as N → ∞ 
# (10 + √N は N^(1/2 + γ) と比べて高次元の無限小で、早く0に収束する)
# we write 10 + √N = o(N^(1/2 + γ))

a5(N) = 10 + sqrt(N)
Ninvλa5(N, λ) = a5(N) / N^(λ)
Nλ(N, λ) = N^λ

anim = @animate for N in 1:N_inf
    p1 = plot(Nλ.(Vector(1:N), 2), markershape=:circle, label=L"N^{2}", xlabel=L"N", ylabel=L"N^\lambda, a_N" , ylims=(0, 50))
    plot!(Nλ.(Vector(1:N), 1/2), markershape=:circle, label=L"N^{1/2}")
    plot!(Nλ.(Vector(1:N), 0.1), markershape=:circle, label=L"N^{0.1}")
    plot!(a5, Vector(1:N), markershape=:circle, xlabel=L"N", label=L"a_N = 10 + \sqrt{N}")    
    p2 = plot(Ninvλa5.(Vector(1:N), 2), markershape=:circle, label=latexstring(L"a_N / N^{2}", "is bounded"), xlabel=L"N", ylabel=L"N^{-\lambda}a_N")
    plot!(Ninvλa5.(Vector(1:N), 1/2), markershape=:circle, label=latexstring(L"a_N / N^{1/2}", "is converged"))
    plot!(Ninvλa5.(Vector(1:N), 0.1), markershape=:circle, label=latexstring(L"a_N / N^{0.1}", "is unbounded"))
    plot(p1, p2, layout=(2, 1))
end
gif(anim, "5_landau_sqrt.gif", fps=60)

$a_N = 10 + \sqrt{N}$と$N^\lambda$との発散スピードを比較すると，$\lambda=2$のとき，上のプロットから$N^{2}$は$a_N$よりも発散スピードが速いので，$\frac{a_N}{N^2}$は$0$に収束してます(下のプロット)．

$$a_N = 10 + \sqrt{N} = \mathcal{o}(N^{\frac{1}{2} + \frac{1}{2}})$$

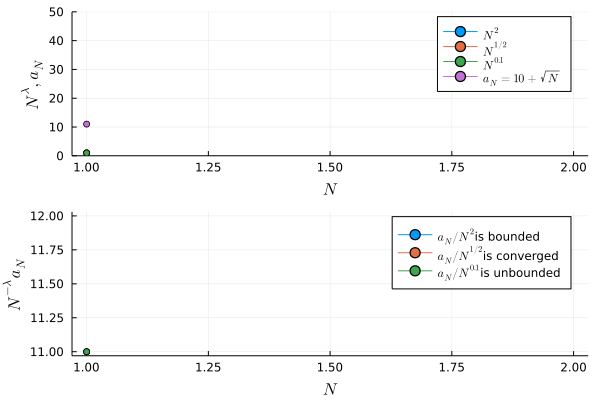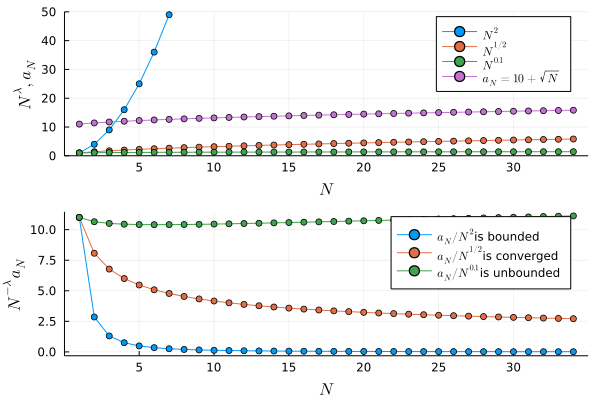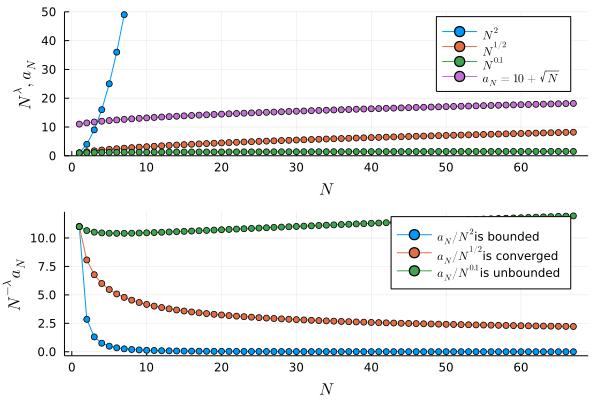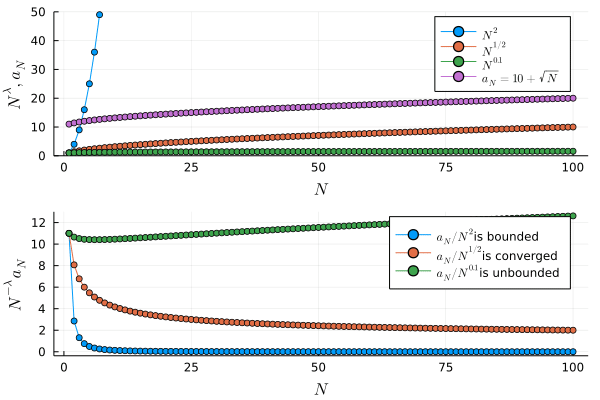
一方，$\lambda=\frac{1}{2}$のとき，$N^{\frac{1}{2}}$は$a_N$と同じ発散スピードなので，$a_N$は$N^{\frac{1}{2}}$に抑えられるような形で$\frac{a_N}{N^{\frac{1}{2}}}$は極限$1$に収束します．

$$a_N = 10 + \sqrt{N} = \mathcal{O}(N^{\frac{1}{2}})$$

ちなみに，$\lambda = 0.1 < \frac{1}{2}$の場合は，$N^{0.1}$は$a_N$よりも発散スピードが遅いので，$\frac{a_N}{N^2}$収束せず発散します．

次回は確率変数の数列の収束について見ていきます．

Reference
Wooldridge, J. M. (2010). Econometric analysis of cross section and panel data second edition. MIT press.