📈

【Juliaで因果推論】回帰分析 - OLS推定とその仮定

2022/05/27に公開

Julia

2つの仮定 $E[U]=0, E[U|X]=E[U]$ が成り立てば，線形回帰モデル $Y=\beta_0 + \beta_1 X + U$ の係数 $β_1$ のOLS推定値はXがYに与える(平均的な)因果効果を意味する．
2つの仮定から，Zero conditional mean $E[U|X]=0$ が成り立つので， CEF: $E[Y|X] = \beta_0 + \beta_1 X$ が母集団で成り立つ．
仮定に基づき線形回帰モデルをモーメント法による推定をすると，結果として最小二乗誤差を最小化するような(OLS)係数パラメータの推定値が得られる．

回帰分析は，他の変数を一定に(コントロール)して推定し，2つの変数間の因果関係を見出す最も代表的な方法の1つです．しかし，推定した結果が因果効果であると信用に値するものとなるためには，ある条件(仮定)が満たされていることが必要となります．仮に仮定が満たされていなければ，いくら"回帰分析"をしたとしてもその結果は因果効果として解釈できません．よって因果推論を目的とする回帰分析では，この仮定を理解することが重要となります．

母集団(population)と標本(sample)

私たちが分析で知りたいことは，興味の対象となる集合全体の中で， $X$ と $Y$ にどんな因果関係があるかです．この集合全体が 母集団(population) です．もちろん母集団は分析によって異なります(e.g. 日本全国の成人，全世界の店舗)．一方，実際にデータとして得られるのは，母集団のうちの一部であり，これが 標本(sample) です．私たちが興味をもっているのは，標本だけにみられる $X$ と $Y$ の関係性ではなく，あくまでも母集団における $X$ と $Y$ の関係性です^[1]．よってこれからやることは，手元のデータである標本から母集団の関係を推測することです．分析する際は，どんな母集団における因果関係が知りたいのかを意識しておくと良いでしょう．

Population model

2つの変数, $X$ （e.g. 教育）と $Y$ （e.g. 賃金）があり，母集団において $X$ (の変化)が $Y$ (の変化)にどのような影響を与えるかを知りたいとしましょう^[2]．このとき3つの問題が出てきます．

$X$ 以外に $Y$ を説明する要因が存在するとき，どう対処すればいいか？
$X$ と $Y$ はどのように関係しているか(どんな関数形か)？
どのように相関関係と因果関係を区別し，他の条件を一定にしたときの $X$ が $Y$ に与える因果効果を抽出できるか？

回帰分析をする際はまず頭の中で，以下のモデルが母集団で成り立っている，またはデータ生成プロセスである(と少なくとも近似できる)と考えます(population model)．

Y = \beta_0 + \beta_1 X + U

このモデルを線形回帰モデルといいます．因果関係を想定するとモデルに意味が見出されます．因果が目的であれば(モデルが正しいかどうかはさておき)このモデルの見方は，右辺が原因で左辺が結果を表わします．

$Y$ は被説明変数(従属変数，Outcome)といい，観測される確率変数です．
$X$ は説明変数(独立変数)といい，観測される確率変数です．
$U$ は誤差項といい，観測されない確率変数です．
$\beta_0$ (定数項), $\beta_1$ (係数)はパラメータです．観測されない(知りたい)値です^[3]．

\underbrace{Y}_{被説明変数} = \overbrace{\beta_0}^{定数項} + \overbrace{\beta_1}^{係数}\underbrace{X}_{説明変数} + \underbrace{U}_{誤差項}

このモデルが3つの問題にどう対応しているか見てみましょう．まず問題1「 $X$ 以外に $Y$ を説明する要因が存在するとき，どう対処すればいいか」について，XとYの関係が，以下のようになっているとします．

Y = \beta_0 + \beta_1 X

しかし現実の世界は複雑であるため $Y$ は $X$ だけでは決まりません．なので回帰分析では観測されないその他全部の要因を $U$ としてモデルに含めてます．線形回帰モデルに $U$ を入れることで， $X$ 以外の， $Y$ に影響は与えるけど観測されない(手元にデータとしてない)さまざまな要因が"考慮"されます．

問題2「 $X$ と $Y$ はどのように関係しているか(どんな関数形か)？」について，線形回帰モデルでは， $X$ と $Y$ の間に線形の関係があると想定します．線形な関係であると，他の条件を一定にしたときの $X$ の変化と $Y$ の変化の関係がシンプルに出てきます．"線形"な感じを見てみましょう．他の条件を一定をするということは，今のモデルで言うとその他の要因を表す誤差項 $U$ を固定する，つまり $U$ の変化がない( $\Delta U=0$ )ということになります． $\Delta U=0$ ときの $Y$ の変化( $\Delta Y$ )と $X$ ( $\Delta X$ )の変化の関係は，線形回帰モデルより，

\Delta Y = \beta_1 \Delta X \quad \text{if} \quad \Delta U = 0

となり，「 $U$ を一定にしたとき， $Y$ の変化は $X$ の変化に $\beta_1$ (傾き)をかけたもの」であるとモデルが想定していることになります．かなり因果効果に近づいてきましたが，この時点ではまだ $X$ が $Y$ に与える因果効果は $\beta_1$ であるとは言い切れません． $U$ を固定できるかどうかまだわからないからです．最後の問題3がカギとなりますが，問題3は最も難しい問題です．

ちなみに，なぜ線形な関係を仮定するのでしょうか？1つの理由として，計算が楽だからです．しかし現実の世界は複雑で，単純な線形関係では $X$ と $Y$ の関係を表現できないと考えるのが普通です．これについてですが，現実の $X$ と $Y$ の関係が非線形でも，回帰分析は複雑な関係に対してベストな線形に近似された関係を与えます(Angrist and Pischke, 2008, p.29)．因果推論の分析はあくまでも人間が理解するためのものなので，正確に現実の個々のデータを予測できるような複雑なモデルは最優先事項ではありません．たとえ線形回帰モデルが現実のデータ生成プロセスと厳密に等しくなくても，近似できていれば^[4]因果関係の解釈は可能です．とはいってもモデルとデータのフィットが良いに越したことはありません．そこでデータを変換(e.g. 対数変換, $n$ 乗項)することで，線形回帰モデルのフレームワークのままデータとのフィットが良くなるケースもあります．線形回帰モデルはかなり柔軟なモデルであり，線形の仮定は思ってるよりも強くはないです．

一番難しい問題3「どのように相関関係と因果関係を区別し，他の条件を一定にしたときの $X$ が $Y$ に与える因果効果を抽出できるか？」について，問題の言葉が少しふんわりしてるので議論しやすいように具体的に言い換えます．

データを使って線形回帰モデルを推定したときに、因果効果として信用に値するような $\beta_1$ の推定値を得ることができるか？

$\beta_1$ は直接観測されないパラメータです．データではありません．母集団における $X$ と $Y$ の関係性を表すパラメータの真の値 $\beta_1$ は永遠に分かりません．分からないのでデータを使って「推定」して $\beta_1$ の推定値を求めます．さて，問題3の言い換えはできましたが，結局モデルの $\beta_i$ は $X$ が $Y$ に与える因果効果として信用できるのでしょうか？答えはモデルをどう推定するか(そのモデルの推定に必要な仮定が満たされているかどうか)に依存します．

ここでは，線形回帰モデルを推定する最も基本的で代表的な方法，最小二乗法(Ordinary Least Squares: OLS)^[5]について考えます．すると問題3はさらに具体的になります．

線形回帰モデルをOLS推定したとき，信用に値するような $\beta_1$ の推定値を得ることができるか？

だいぶ具体的になりました．この問題に対してならはっきり答えられます．答えは2つの仮定，

$E[U]=0$ (誤差項 $U$ の期待値はゼロ)
$E[U|X]=E[U]$ (誤差項 $U$ の期待値は説明変数 $X$ の値に依存しない)

が成り立っていればOLS推定で得られる $\beta_1$ の推定値は因果効果として信用できます．OLS推定の実際の推定方法に入る前に大事な大事なこの2つの仮定について見ていきましょう．

仮定1: $E[U]=0$

1つ目の仮定は，誤差項 $U$ の期待値がゼロ であることです．母集団を意識した言葉を使えば，「母集団の観測されない要素 $U$ の分布の期待値はゼロ」です．実はこの仮定は大したことなく，容易に成り立たせることができます．

定数項のある線形回帰モデルを見てみましょう．ただし誤差項の期待値はゼロではない何らかの値( $E[U]=\alpha_0 \neq 0$ )である状況だとします．

Y = \beta_0 + \beta_1 X + U, \quad E[U] = \alpha_0 (\neq 0)

このままだと一見，仮定 $E[U]=0$ が満たされていないように見えますが，モデルの定数項だけ変えることで仮定1を満たすことができます．

\begin{align*} Y & = \beta_0 + \beta_1 X + U, \quad E[U] = \alpha_0 (\neq 0) \\ & = \underbrace{(\beta_0 + \alpha_0)}_{\delta_0} + \beta_1 X +\underbrace{(U - \alpha_0)}_{V} \\ & = \delta_0 + \beta_1 X + U \end{align*}

新しいモデルは定数項が $\delta_0 = \beta_0 + \alpha_0$ に変わっただけで，興味の対象である係数パラメータ $\beta_1$ は変わっていません．確率変数である誤差項 $U$ から $\alpha_0$ を引いているので新しい誤差項 $V=U-\alpha_0$ の期待値はゼロとなります( $E[V]=0$ )．従って定数項をモデルに入れている限り，定数項が変わるので必然的に誤差項の期待値はゼロとなります．

ちなみに定数項は $X$ に依存しない( $X=0$ の時の) $Y$ のベースラインと解釈されます．あまり分析の興味の対象にはなりませんが，線形回帰モデルをOLS推定するときは仮定1を成り立たせるという目的で，必ずモデルに入れましょう．

仮定2: $E[U|X]=E[U]$ (Mean Independence)

2つ目の仮定はとても重要です．仮定1と違い，仮定2は $U$ と $X$ の関係性について議論しています．

そもそも，条件付期待値 $E[U|X]$ は，" $X$ が与えられた時の $U$ の期待値"という意味であり，確率変数 $X$ の関数です．条件付期待値 $E[U|X]$ を視覚的にイメージすると，2つの確率変数 $U, X$ の母集団における(同時)分布に対して，片方の $X$ のある値で条件付け（i.e. 固定, コントロール，"スライス")したときの $U$ だけの分布の期待値となります．

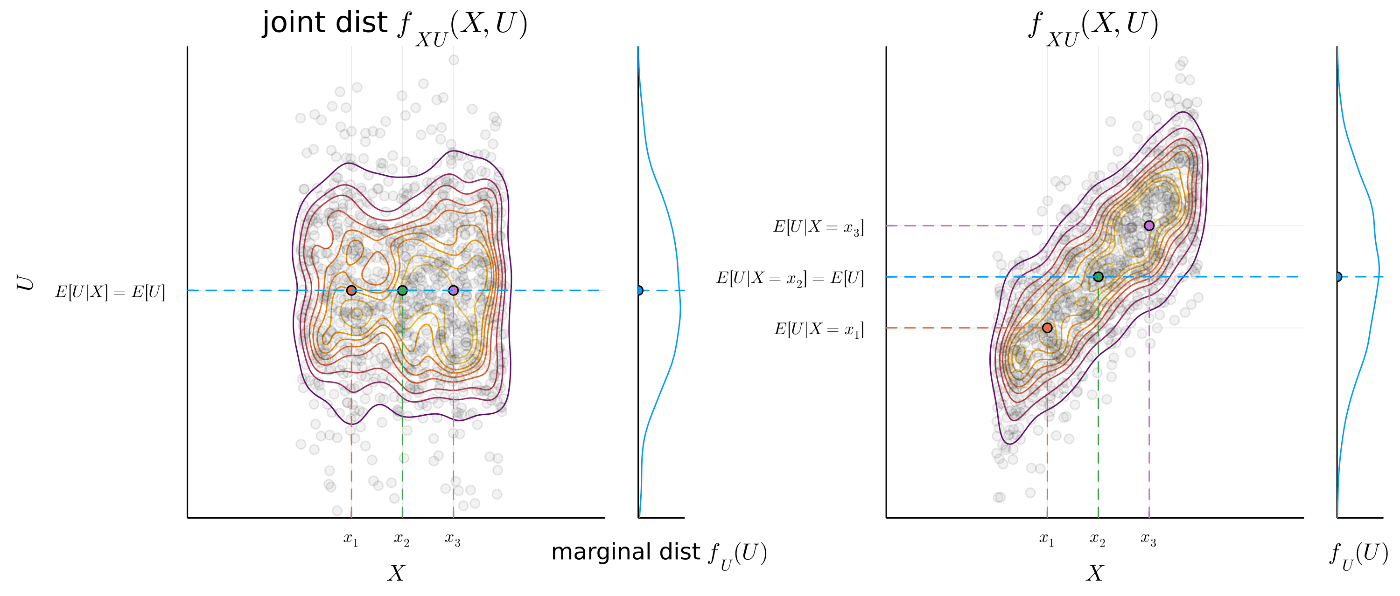
mean_independence
Figure.1 Mean independence のイメージ．
左: $E[U|X]=E[U]$ ，右: $E[U|X] \neq E[U]$

よって仮定2 $E[U|X]=E[U]$ は， $X$ で条件付けした $U$ の期待値 $E[U|X]$ が $X$ とは関係ないただの $U$ の期待値 $E[U]$ と等しいという意味です．ざっくり言い換えれば 誤差項 $U$ の期待値は説明変数 $X$ の値に依存しない ということになります．

$E[U|X]=0$ (zero conditional mean assumption)

2つの仮定が成り立っていると

E[U|X]=E[U]=0

となり， $E[U|X]=0$ (zero conditional mean assumption)というオーバーオールな仮定が成り立つことになります．この仮定は，観測されない要因 $U$ と説明変数 $X$ に関する非常に重要な仮定です．また， $E[U|X]=0$ が成り立っていれば， $X$ と $U$ の間に相関がない ( $Cov(U, X)=0$ )ことが成り立つことが必要です．

Proof: $E[U|X]=0 \rightarrow Cov(U, X)=0$

$E[U|X]=0$ と繰り返し期待値の法則より，

\begin{align*} E[UX] & = E[E[UX|X]] = E[XE[U|X]] = 0 \\ \\ Cov[U, X] & = E[UX] + E[U]E[X] \\ & = 0 + 0 E[X] \\ & = 0 \end{align*}

モデルを議論する際，条件付期待値は直接イメージしにくいため^[6]，代わりに必要条件である

Cov(U, X)=0, \quad (XとUの間に相関がない)

が成り立っているかどうか考えるとスムーズです^[7]．

実際に $X$ と $U$ の間に相関がないという仮定が成り立つかどうかは，モデルを見ながら考えます．今回は身長( $Height$ )と賃金( $Earnings$ )の例(Stock and Watson, 2018)^[8]で見てみましょう．

using CSV, DataFrames, Plots, StatsPlots, Statistics
df = CSV.read("Earnings_and_Height.csv", DataFrame)

scatter(df.height, df.earnings, alpha=0.05, legend=false, xlabel="height (inches)", ylabel="annual labor earnings (dollars)")

earning_height

次のような線形回帰モデルを考えます．

Earnings = \beta_0 + \beta_1 Height + U \\

このモデルによる $\beta_1$ のOLS推定値は，身長が賃金に与える因果効果として適切でしょうか？つまり， $Height$ と $U$ の間に相関はあるでしょうか？説明変数と誤差項間に相関が生じるメカニズムは様々ですが，一番わかりやすいものは 欠落変数(omitted variable) によるものです．

欠落変数の見つけ方は2ステップです．

説明変数 $X$ 以外で従属変数 $Y$ に影響を与える要因 $Z$ を考える．
- その要因 $Z$ は今，モデルに含まれてないので，誤差項 $U$ の中に入っていることになります．
モデルに入っていない要因 $Z$ と説明変数 $X$ に相関があるか考える．
- もし相関があれば， $Z$ は $U$ の一部なので， $X$ と $U$ も相関することになり， $E[U|X]=0$ の仮定が満たされなくなります．

例えばモデルに含まれていない要因 $U$ のうち，男性か女性かという変数 $Sex$ (男性ならば1，女性ならば0)は $Earnings$ に影響を与えると考えられます．男性と女性では身長の傾向は異なるので， $Sex$ と $Height$ は(正に)相関するはずです．そうなると $Sex$ はモデルの $U$ の一部なので， $Height$ と $U$ が相関することになり， $E[U|Height]=0$ の仮定が満たされず，このモデルによる $\beta_1$ のOLS推定値は因果効果として信用できないことになります．

Earnings = \beta_0 + \beta_1 Height + \underbrace{U}_{Sex \text{が含まれる}}

$Sex \rightarrow Earnings$ : $Sex$ は $Earings$ に影響を与えそう
$Cov[Height, Sex] \neq 0$ : $Height$ と $Sex$ は相関がありそう^[9]

本当に相関があるかないか分からなくても，モデルの議論においては相関がありそうという時点で， $\beta_1$ のOLS推定値は因果効果として適切でない可能性が生まれて信用できなくなります．よって，相関がありそうかなさそうかの判断は，ガチガチの理論でなくても，常識や経験，妄想の範囲で相関の可能性を考えるだけでも十分に機能します．

ちなみにデータを見ると，女性か男性か( $Sex$ )と身長( $Height$ )はかなり正に相関しています( $Cor[Sex, Height]\simeq0.7$ )．よって，このモデルの $\beta_1$ の推定値は因果効果として信用できない可能性があります．

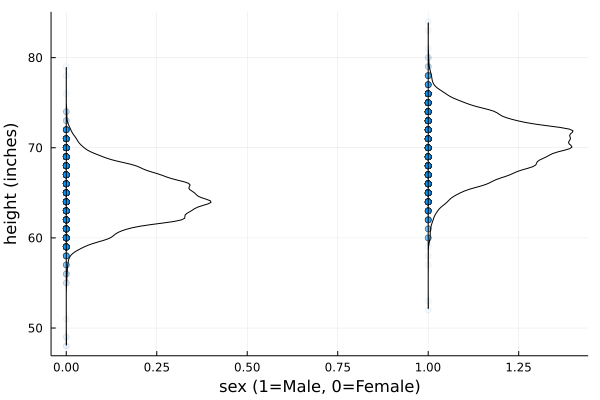
gdf = groupby(df, :sex)
scatter(gdf[2].height, gdf[2].earnings, alpha=0.05, label="male", xlabel="height (inches)", ylabel="annual labor earnings (dollars)")
scatter!(gdf[1].height, gdf[1].earnings, alpha=0.05, label="female")

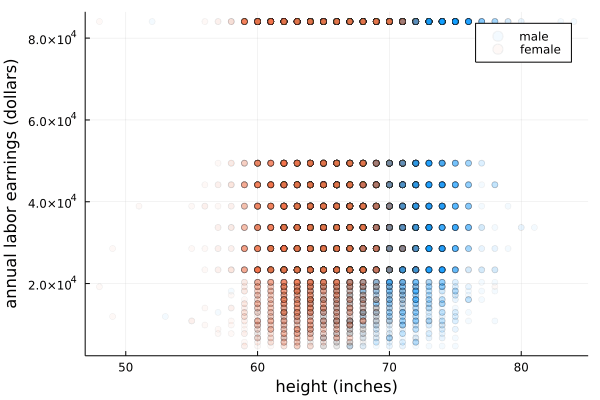
earning_height_by_sex

scatter(df.sex, df.height, alpha=0.05, legend=false, xlabel="sex (1=Male, 0=Female)", ylabel="height (inches)")
violin!(df.sex, df.height, side=:right, fillalpha=0, linewidth=1, label=false)

height_sex

cor(df.height, df.sex)
# 0.6998784100114194

Conditional Expectation Function: CEF

もし $E[U|X]=0$ が成り立っているとすると，線形回帰モデル( $Y = \beta_0 + \beta_1 X + U$ )の両辺に $X$ に関する条件付期待値^[10]をとると，

\begin{align*} E[Y|X] & = E[\beta_0 + \beta_1 X + U | X] \\ & = \beta_0 + \beta_1 X + E[U | X] \\ \\ E[Y|X] & = \beta_0 + \beta_1 X \end{align*}

となります． $E[Y|X]$ を母集団の回帰線(population regression function: PRF)またはconditional expectation function: CEF (Angrist and Pischke, 2008)といいます． $E[Y|X]$ は $X$ の関数であるので， $X$ の値がわかれば(e.g., $X=x$ )，代入して $Y$ の平均的な値を特定できます(e.g. $E[Y|X=x]=\beta_0 + \beta_1 x$ )．つまり，CEFである $E[Y|X]$ は $X$ のそれぞれのレベルと，それに対応する $Y$ の平均的な値の関係性を表しています．

私たちが知りたいのは，標本の $Y$ の個々の値ではなく，母集団における $Y$ の(分布の)平均です．よってCEFはまさに私たちが知りたいものとなります．当たり前ですがCEFは $Y$ の(条件付)期待値なので，あくまでも平均的な傾向としての関係をとらえています．決して「全てのサンプルが個々に必ず満たす関係性」ではないことです．例えば，高校のTOEICの点数 $hsTOEIC$ と大学のTOEICの点数 $colTOEIC$ に次のようなCEFが成り立つとします．

E[colTOEIC|hsTOEIC] = 500 + 0.5 hsTOEIC

このCEFは，高校のTOEICの点数 $hsTOEIC$ が与えられた時の，平均的な大学のTOEICの点数 $colTOEIC$ を示しています． $hsTOEIC=400$ の人は，平均的には大学のTOEICの点数が $E[colTOEIC|hsTOEIC=400] = 500 + 0.5 \times 400 = 700$ ， $hsTOEIC=600$ の人は，平均的には大学のTOEICの点数が $E[colTOEIC|hsTOEIC=600] = 500 + 0.5 \times 600 = 800$ ，といった具合です．
もちろん中には $hsTOEIC=600$ でも，モデルに含まれていない要因 $U$ によって $colTOEIC$ が $800$ より低い人や高い人もいますが，CEFはあくまでも高校のTOEICの点数が高い人ほど 平均的には 大学のTOEICの点数は高くなるという関係性を示しています．

Figure.2 母集団の回帰直線(CEF) $E[Y|X] = \beta_0 + \beta_1 X$

現実の世界で起きている事象の多くはランダムですが，ランダムの中でも手元のデータから解釈できるメカニズムの部分と，データではわからない部分が存在します． $E[U|X]=0$ が成り立てば，現実のデータ $Y$ は $X$ で説明できる部分 $E[Y|X]$ (systematic part)と $X$ では説明できない部分 $U$ (unsystematic part)に分けることができます．

Y = \underbrace{E[Y|X]}_{\text{systematic part}} + \underbrace{U}_{\text{unsystematic part}}

もし $E[U|X]=0$ が成り立っているのであれば， $U$ と $X$ は関係ないことが保証されます．すると， $X$ と $Y$ の因果関係ついてはCEFの $E[Y|X] = \beta_0 + \beta_1 X$ で完結され，パラメータ $\beta_1$ を $X$ が $Y$ に与える因果効果として解釈できるようになります^[11]．

仮定に基づくモデルの推定

線形回帰モデルを推定するときに必要な2つの仮定を確認したうえで，いよいよモデルの推定方法(係数パラメータの求め方)に移ります．実際の推定も仮定ベースで進むので，繰り返しますが2つの仮定は重要です．

まず，推定するためには標本が必要です．母集団から $N$ 個^[12]の $X$ と $Y$ の組を(ランダムに)抽出し，サンプルとします．

\left\{(X_i, Y_i): i = 1, \ldots, N \right\}

$i$ は(e.g. 個人 $i$ , 企業 $i$ )は分析単位(unit)を識別するノーテーションです^[13]．

母集団で平均的に成り立つ(と思う)回帰モデルは

Y = \beta_0 + \beta_1 X + U

でした．母集団で平均的に成り立つモデル(関係性)はサンプルでも平均的に成り立つ という自然なアイディアから，サンプルの回帰モデル

Y_i = \beta_0 + \beta_1 X_i + U_i

を用意しておきます．このモデルは後で使います．

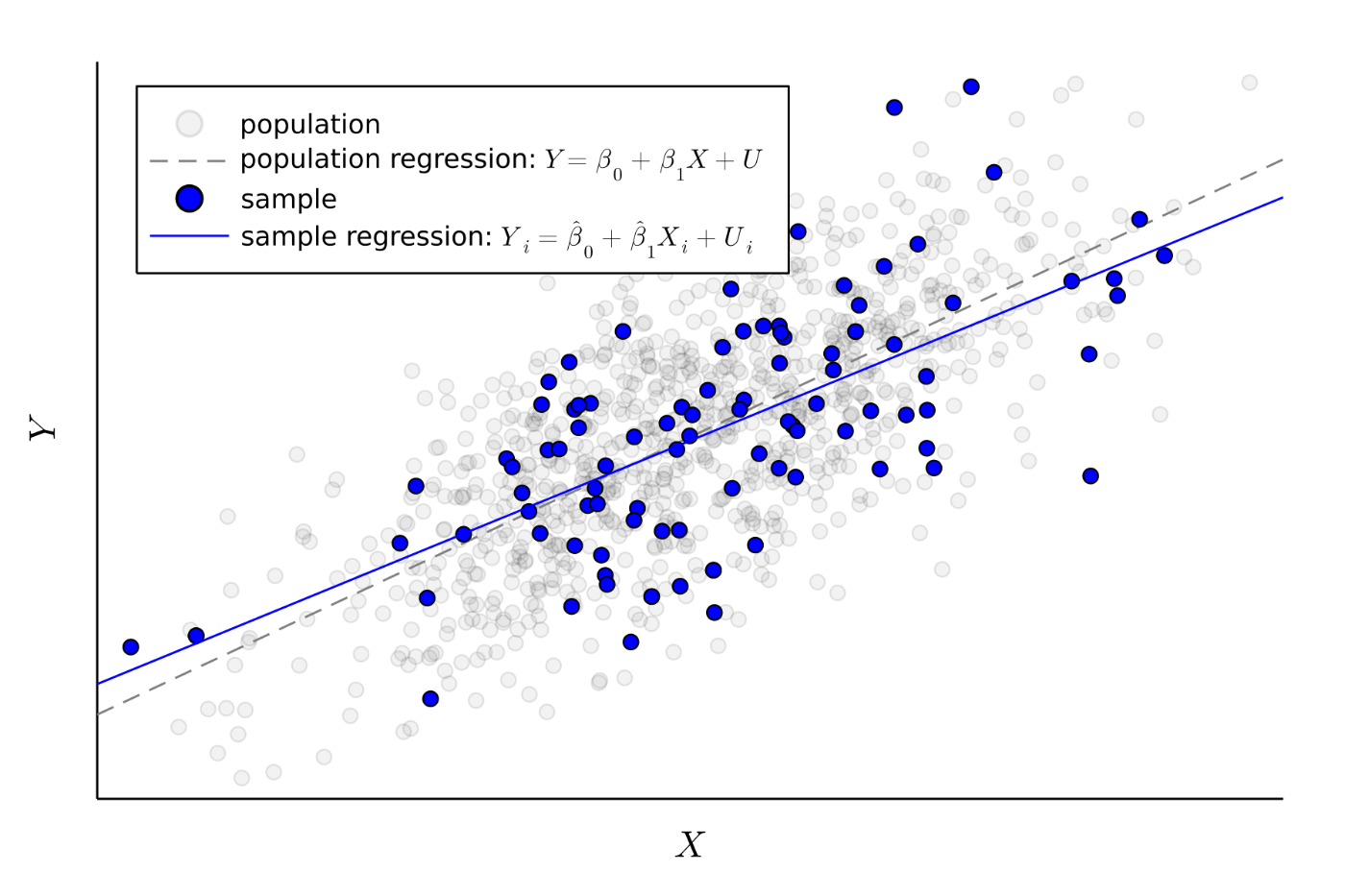
ppl_spl_reg
Figure.3 母集団回帰と標本回帰のイメージ

まずは母集団で2つの仮定から示される $X$ と $Y$ の条件式を見てみます．2つの仮定より，

\begin{align*} E[U] & = 0 \quad & (仮定1) \\ Cov[U, X] = E[XU] & = 0 \quad & (仮定1 \& 仮定2) \end{align*}

が成り立ちます．ここで，母集団の回帰モデルより， $U = Y - \beta_0 - \beta_1 X$ を代入すると^[14]，

\begin{align*} E[Y - \beta_0 - \beta_1 X] & = 0 \quad & 母集団のY - \beta_0 - \beta_1 Xの期待値はゼロ \\ E[X(Y - \beta_0 - \beta_1 X)] & = 0 \quad & 母集団のX(Y - \beta_0 - \beta_1 X)の期待値はゼロ \end{align*}

が得られます．これは，母集団で回帰モデルと仮定1と仮定2が成り立つために必要な，母集団における $X$ と $Y$ (の同時分布)に対する条件(制約)式です^[15]．よって，この母集団の条件を満たすようなパラメータ $\beta_0, \beta_1$ さえ見つけることができれば，仮定1と仮定2は成立し，CEFをもとに $\beta_1$ は「 $X$ が1単位増えたときの $Y$ に与える因果効果」として解釈できるようになります．

しかし私たちは母集団を扱うことはできないため，母集団から直接パラメータ見つけることはできません．そこで母集団で成り立つ仮定はサンプルでも成り立つという自然なアイディアから，母集団における条件式をサンプルに置き換えて，私たちがデータを用いて対処できるようにします．2つの仮定がサンプルでも成り立つのであれば，母集団の時と同様に今度はサンプルの回帰から， $U_i = Y_i - \beta_0 - \beta_1 X_i$ を代入すると以下のようなサンプルにおける条件式^[16]が得られます．

\begin{align*} \frac{1}{N}\sum_{i=1}^N[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] & = 0 \quad & サンプルのY - \hat{\beta_0} - \hat{\beta_1} Xの標本平均はゼロ \\ \frac{1}{N}\sum_{i=1}^N X_i[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] & = 0 \quad & サンプルのX(Y - \hat{\beta_0} - \hat{\beta_1} X)の標本平均はゼロ \end{align*}

母集団の条件式と見比べると，期待値のオペレーター $E[\cdot]$ が標本平均のオペレーター $\frac{1}{N}\sum_{i=1}^N[\cdot]$ に変わっただけです．パラメータにハット $\hat{\cdot}$ がついているのは，母集団のパラメータを推定したものだからです^[17]． $(X_i, Y_i)$ はサンプルなので，この条件を満たすようなパラメータ $\hat{\beta_0}, \hat{\beta_1}$ はデータを用いて見つけることができます．未知数2つ，条件2つなので， $\hat{\beta_0}, \hat{\beta_1}$ は一意に決まります．解いてみましょう．

Solve $\hat{\beta_0}, \hat{\beta_1}$ :

まず，1つ目の条件 $\frac{1}{N}\sum_{i=1}^N[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] = 0$ について，

\begin{align*} \frac{1}{N}\sum_{i=1}^N[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] & = 0 \\ \frac{1}{N}\sum_{i=1}^N Y_i - \hat{\beta_0} \frac{1}{N}\sum_{i=1}^N 1 - \hat{\beta_1} \frac{1}{N}\sum_{i=1}^N X_i & = 0 \\ \bar{Y} - \hat{\beta_0} - \hat{\beta_1} \bar{X} & = 0 \\ \hat{\beta_0} & = \bar{Y} - \hat{\beta_1} \bar{X} \end{align*}

$\bar{Y}=\frac{1}{N}\sum_{i=1}^N Y_i, \bar{X}=\frac{1}{N}\sum_{i=1}^N X_i$ は標本平均なので，データから計算できる数値(定数)です． $\hat{\beta_0}$ を $\hat{\beta_1}$ で表すことができたので， $\hat{\beta_0} = \bar{Y} - \hat{\beta_1} \bar{X}$ を2つ目の条件 $\frac{1}{N}\sum_{i=1}^N X_i[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] = 0$ に代入します．

\begin{align*} \frac{1}{N}\sum_{i=1}^N X_i[Y_i - \hat{\beta_0} - \hat{\beta_1} X_i] & = 0 \\ \frac{1}{N}\sum_{i=1}^N X_i[Y_i - (\bar{Y} - \hat{\beta_1} \bar{X}) - \hat{\beta_1} X_i] & = 0 \\ \frac{1}{N}\sum_{i=1}^N X_i[Y_i - \bar{Y}] - \hat{\beta_1} \frac{1}{N}\sum_{i=1}^N X_i [X_i - \bar{X}] & = 0 \\ \frac{1}{N}\sum_{i=1}^N X_i[Y_i - \bar{Y}] & = \hat{\beta_1} \frac{1}{N}\sum_{i=1}^N X_i [X_i - \bar{X}] \end{align*}

ここで，和のオペレーターの特性より，

\sum_{i=1}^N X_i [X_i - \bar{X}] = \sum_{i=1}^N [X_i - \bar{X}]^2, \quad \sum_{i=1}^N X_i[Y_i - \bar{Y}] = \sum_{i=1}^N [X_i - \bar{X}][Y_i - \bar{Y}]

を用いると，

\begin{align*} \frac{1}{N} \sum_{i=1}^N [X_i - \bar{X}][Y_i - \bar{Y}] & = \hat{\beta_1} \\ \hat{\beta_1} & = \frac{\frac{1}{N} \sum_{i=1}^N [X_i - \bar{X}][Y_i - \bar{Y}]}{\frac{1}{N} \sum_{i=1}^N [X_i - \bar{X}]^2} \\ \hat{\beta_1} & = \frac{\sum_{i=1}^N [X_i - \bar{X}][Y_i - \bar{Y}]}{\sum_{i=1}^N [X_i - \bar{X}]^2} \end{align*}

$\hat{\beta_1}$ が求まったので，最後にこれを $\hat{\beta_0} = \bar{Y} - \hat{\beta_1} \bar{X}$ に代入して $\hat{\beta_0}$ を求めます．

\begin{align*} \hat{\beta_0} & = \bar{Y} - \frac{\sum_{i=1}^N [X_i - \bar{X}][Y_i - \bar{Y}]}{\sum_{i=1}^N [X_i - \bar{X}]^2} \bar{X} \end{align*}

よって，仮定に基づく条件式を満たすようなパラメータ $\hat{\beta_0}, \hat{\beta_1}$ は

\begin{align*} \hat{\beta}_0^{MM} & = \bar{Y} - \hat{\beta_1} \bar{X} \\ \hat{\beta}_1^{MM} & = \frac{\sum_{i=1}^N (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^N (X_i - \bar{X})^2} \end{align*}

と推定されます．このような母集団のパラメータ(e.g. $\beta_0, \beta_1$ )をサンプルから推定するもの(システム，確率変数の関数=確率変数)を母集団のパラメータの推定量(estimator)(e.g. $\hat{\beta}_0, \hat{\beta}_1$ )といいます^[18]．この推定量の形， $\frac{\sum_{i=1}^N (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^N (X_i - \bar{X})^2} = \frac{XとYの共分散っぽいもの}{Xの分散っぽいもの}$ はちょくちょく出てきます．この形に慣れておきましょう．分子分母に $\frac{1}{N}$ をかければ， $\frac{\frac{1}{N} \sum_{i=1}^N (X_i - \bar{X})(Y_i - \bar{Y})}{\frac{1}{N} \sum_{i=1}^N (X_i - \bar{X})^2} = \frac{XとYの標本共分散}{Xの標本分散}$ となります^[19]．

ちなみにこの，「母集団で成り立つ関係はサンプルでも成り立つはず」というアイディアから，母集団のモーメント条件(population moment condition)をもとにサンプルのモーメント条件(sample moment condition)を立ててパラメータを推定する方法をモーメント法(Method of Moments: MM)といい，得られるパラメータの推定量 $\hat{\beta}_0^{MM}, \hat{\beta}_1^{MM}$ をモーメント法推定量といいます．

ところで，MM推定量に基づきデータから計算された推定値(推定量の実現値)によって，あらゆる $X_i$ に対応する $Y_i$ の値がモデルによって推計(予測, fit)できます．

\hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_i

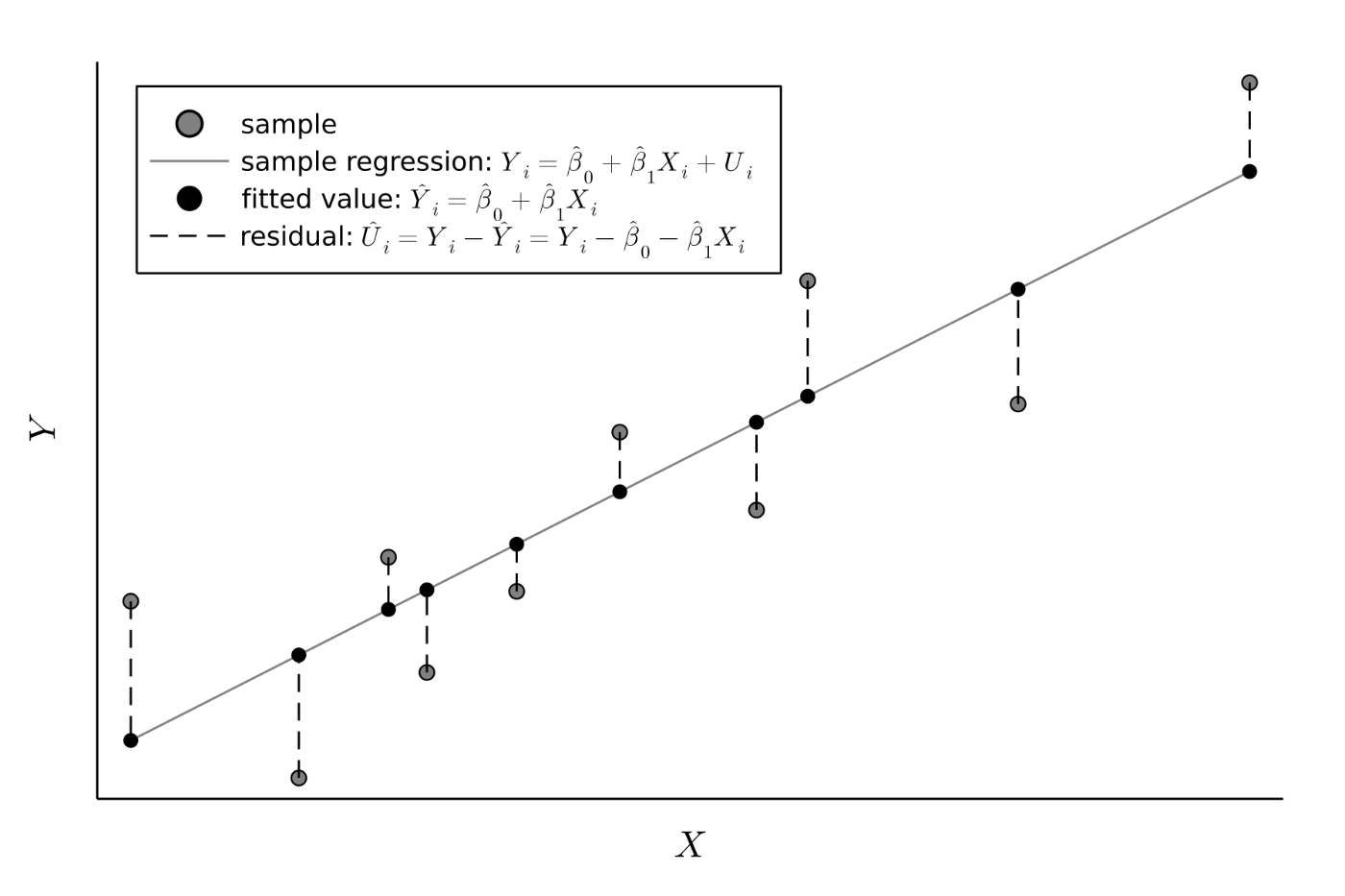
$\hat{Y}_i$ はモデルが予測する値，推計値(predicted value, fitted value)です．モデルがどれだけ"うまく"予測できているかは，残差(residual) $\hat{U}_i$ を見ます^[20]．

\begin{align*} \hat{U}_i & = Y_i - \hat{Y}_i \\ & = Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i \end{align*}

residual
Figure.4 推計値と残差のイメージ

全てのサンプルに対して平均的にどれだけうまく予測できたかは，残差の二乗和(sum of squared residuals)^[21]を指標として見ます．

\begin{align*} \sum_{i=1}^N \hat{U}_i^2 & = \sum_{i=1}^N (Y_i - \hat{Y}_i)^2 \\ & = \sum_{i=1}^N (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2 \end{align*}

"良い"モデルとして，残差の二乗和を最小にするような(予測精度が最も高い)モデルが考えられます．つまり，残差の二乗和を最小にするようなパラメータ $\hat{\beta}_0, \hat{\beta}_1$ は

\begin{align*} \{\hat{\beta}_0^{OLS}, \hat{\beta}_1^{OLS} \} & = \text{argmin}_{\hat{\beta}_0, \hat{\beta}_1} \left( \sum_{i=1}^N \hat{U}_i^2 \right) \\ & = \text{argmin}_{\hat{\beta}_0, \hat{\beta}_1} \left( \sum_{i=1}^N (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2 \right) \end{align*}

ですが，実はこの"良い"モデルのパラメータはMM推定で得られるパラメータ $\hat{\beta}_0^{MM}, \hat{\beta}_1^{MM}$ と一致します．

Solve $\{\hat{\beta}_0^{OLS}, \hat{\beta}_1^{OLS} \} = \text{argmin}_{\hat{\beta}_0, \hat{\beta}_1} \left( \sum_{i=1}^N (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2 \right)$ :

$\hat{\beta}_0$ の一階の条件^[22]より，

\begin{align*} -2 \sum_{i=1}^N (Y_i - \hat{\beta_0} - \hat{\beta_1} X_i) &= 0 \\ \sum_{i=1}^N (Y_i - \hat{\beta_0} - \hat{\beta_1} X_i) &= 0 \end{align*}

$\hat{\beta}_1$ の一階の条件より，

\begin{align*} -2 \sum_{i=1}^N X_i (Y_i - \hat{\beta_0} - \hat{\beta_1} X_i) &= 0 \\ \sum_{i=1}^N X_i (Y_i - \hat{\beta_0} - \hat{\beta_1} X_i) &= 0 \end{align*}

これはサンプルのモーメント条件と一致します．

よって結果的に「残差の二乗和を最小にするような $\hat{\beta}$ を選ぶ」推定(最小二乗法, Ordinary Least Square: OLS)と「母集団の仮定に対応するサンプルの仮定を満たすような $\hat{\beta}$ を選ぶ」MM推定は同じ推定量・推定値が得られます．ですがMM推定は高度な回帰分析手法を理解するうえでも非常に有用なものとなるので，MM推定に着目します^[23]．

データを使ったOLS推定のシミュレーション

式で線形回帰モデルの推定の仕方がわかったので，データを使ってプログラムで推定してみましょう．まずは，自分で真の値を設定して仮想データを自作し，シミュレーションでモデルのOLS(MM)推定値と真の値を比べてみましょう．

シミュレーションでは私たちが神様なので母集団のパラメータを好きな値に設定できます．ここでは定数項の真の値を $\beta_0=3.0$ ，係数パラメータの真の値を $\beta_1=5.5$ とします．母集団でのデータ生成プロセスは以下の通りとします^[24]．

Y = 3.0 + 5.5 X + U, \quad U \sim \mathcal{N}(0, 1)

仮想的な母集団の $X$ と $Y$ の関係は「 $X$ が1単位増えたら $Y$ が $\beta_1=5.5$ 増加する」であり，これが因果効果です．しかし現実では $\beta_1$ 真の値は観測されないため，サンプルから推定するしかありません．そこで真の値を知らない体で，線形回帰モデルを想定し^[25]，線形回帰モデルのパラメータを推定してみましょう．

Y_i = \hat{\beta}_0 + \hat{\beta}_1 X_i + U_i

using Random, Statistics, Plots, LaTeXStrings, Printf

# 真の値を設定: Y = β0 + β1 X + U
β0, β1 = 3.0, 5.5

# 仮想データの生成．
Random.seed!(1)

N = 200
X = rand(Uniform(0, 1), N) # Xは一様分布 U ~ Uniform[0, 1] (どんな分布でもいい)
σ_U = 1
U = rand(Normal(0, σ_U), N) # Uは正規分布 U ~ Normal(0, 1) (どんな分布でもいい)
Y = β0 .+ β1 * X + U

# 線形回帰モデルを想定

# モデルのパラメータの推定, 
β1_hat = cov(X, Y) / var(X)
β0_hat = mean(Y) - β1_hat * mean(X)

print("true params: ", (β0, β1), "\n")
print("estimated params: ", (β0_hat, β1_hat), "\n")

# true params: (3.0, 5.5)
# estimated params: (3.1341948310553907, 5.255470309812545)

# プロット
scatter(X, Y, color=:blue, xlabel=L"X", ylabel=L"Y", label="mock data", legend=:topleft, dpi=300)
Plots.abline!(β1_hat, β0_hat, color=:blue, label=latexstring("OLS: ", L"\hat{Y}_i = ", @sprintf("%.1f", β0_hat), L" + ", @sprintf("%.1f", β1_hat), L"X_i"))
Plots.abline!(β1, β0, color=:black, linestyle=:dash, label=latexstring("True Model: ", L"E[Y|X] = ", @sprintf("%.1f", β0), L" + ", @sprintf("%.1f", β1), L"X"))

sim_ols

真の値とOLS推定値を比べると，真の値 $\{\beta_0, \beta_1\} = \{3.0, 5.5\}$ に対し，推定値は $\{\hat{\beta}_0, \hat{\beta}_1\} \simeq \{3.13, 5.26\}$ とかなり近い値となっています．真の値は本来知らない値なので，データ分析の結果から「平均的には $X$ が1単位増加すると， $Y$ は5.26増加する傾向がある」と報告できそうです^[26]．

次に，実際のデータを使って教育 $Educ$ と賃金 $Earnings$ の関係を推定してみましょう．前のEarnings_HeightのデータセットにEducもあるのでこれを使います．まずはプロットしてデータを見ます．どんな関係がありそうでしょうか？

using CSV, DataFrames, Plots, Statistics
df = CSV.read("Earnings_and_Height.csv", DataFrame)

scatter(df.educ, df.earnings, alpha=0.05, legend=false, xlabel="years of education", ylabel="annual labor earnings (dollars)")

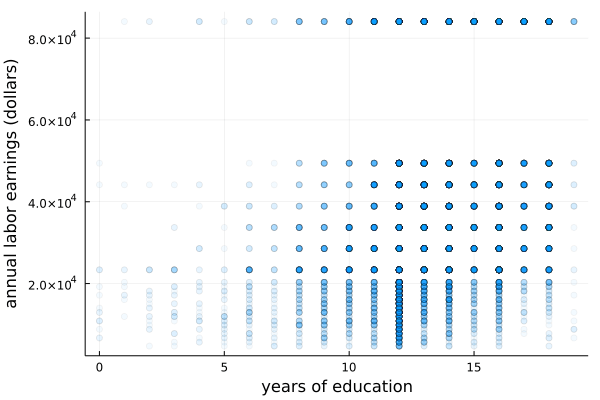
earning_educ

毎回OLS推定値をフルスクラッチ(共分散/分散)で求めるのは面倒です．大体のプログラミング言語や数理統計ソフトには回帰分析のパッケージが備わっているので，使ってみましょう．JuliaであればGLM.jlがいいと思います．

using GLM

linearRegressor = lm(@formula(earnings ~ educ), df)

# earnings ~ 1 + educ

# Coefficients:
# ────────────────────────────────────────────────────────────────────────
#                 Coef.  Std. Error      t  Pr(>|t|)  Lower 95%  Upper 95%
# ────────────────────────────────────────────────────────────────────────
# (Intercept)  -6648.03    969.179   -6.86    <1e-11   -8547.72   -4748.35
# educ          3953.76     70.2676  56.27    <1e-99    3816.03    4091.49
# ────────────────────────────────────────────────────────────────────────

出力される表の1列目Coef.にパラメータの推定値が表示されています．定数項((Intercept))は $\hat{\beta}_0 = -6648.03$ ，傾き(educ)は $\hat{\beta}_1 = 3953.76$ となっています．Coef.以外の数字が意味していることは次回以降説明します．ちなみに，推定量の式を律儀に実装した結果も同じ推定値を与えます^[27]．

# estimate from scratch
β1_hat = cov(df.educ, df.earnings) / var(df.educ)
β0_hat = mean(df.earnings) - β1_hat * mean(df.educ)

print("estimated params: ", (β0_hat, β1_hat), "\n")
# estimated params: (-6648.030688955005, 3953.7613449465175)

結果の解釈ですが，もし $Educ$ と $U$ に相関が無ければ推定値は因果効果として信用でき，「教育年数が1年増えると，平均的に3953.76$増加する傾向がある」と解釈できます．しかし，真の値は観測できないのでこの分析結果が本当に因果効果かどうかは，データだけでは断定できません．また仮定 $E[U|Educ]=0$ が満たされているかどうかも $U$ が観測されない限りデータでは確認できません．重要なのは分析者の考察であり，理論や経験，直感からもし相関がありそう^[28]と判断されると，その時点で推定値は因果効果として信用できないものとなります．

そもそもなぜ「 $X$ と $U$ が相関しない」仮定が満たされないと，OLS推定(MM推定)が与える $\beta_1$ の推定値は信頼できないものになるのでしょうか?，どのようにしたら仮定を満たすことができ，信用に値する分析結果が得られるのでしょうか？次回紹介します．

Refference

Cunningham, S., 2021. Causal inference: the mixtape. Yale University Press.
Huntington-Klein, N., 2021. The effect: An introduction to research design and causality. Chapman and Hall/CRC.
Wooldridge 2012 Introductory Econometrics: A Modern Approach
Stock, J.H. and Watson, M.W., 2018. Introduction to econometrics 4th Edition. Boston: Addison Wesley.
Angrist, J.D. and Pischke, J.S., 2008. Mostly harmless econometrics. In Mostly Harmless Econometrics. Princeton university press.

脚注

標本のみの関係性に基づいた意思決定をして母集団に処置を行っても，思った通りの変化は得られない可能性があるからです． ↩︎
この時点ではまだ因果関係までは想定していません．ただザックリとXの変化によってYがどう変化するかというメカニズムについてを考えます． ↩︎
原則，確率変数は大文字で表します．値や確率変数の実現値は小文字で表します(文献によってまちまちです)．ちなみに，データや変数はアルファベットで表し，統計的に推測される母集団のパラメータ(e.g. $\beta_1$ )はギリシャ文字で表すのが慣習です． ↩︎
モデルがどれだけ現実を近似できているかはまた別の話です．モデルが妥当かどうかを吟味する必要があります． ↩︎
結果的にはOLSと一致しますが導出はMM法でやります．MM法だと高度な回帰分析へと繋げやすいからです． ↩︎
直接zero conditional mean assumptionをイメージしたいときは，Figure.1のように $E[U|X=x_1]=E[U|X=x_1]= \dots$ =0が成り立つかどうかを考えるといいでしょう． ↩︎
必要条件なので， $Cov[U, X]=0$ が成り立っていても $E[U|X]=0$ は成り立たないときもありますが， $Cov[U, X]=0$ が成り立たなければ $E[U|X]=0$ は絶対に成り立ちません．ちなみに $Cov[U, X]=0$ が成り立たない場合，推定に漸近バイアスが生じるので一発アウトです． ↩︎
データはhttps://media.pearsoncmg.com/intl/ge/2019/cws/ge_stock_econometrics_4/content/datapages/stock04_data04.htmlからダウンロードできます． ↩︎
厳密には，「身長の値によっては男女の(分布の)平均は異なりそう」 $E[Sex|Height=h_1] \neq E[Sex|Height=h_2] \neq E[Sex]$ ↩︎
なぜ期待値なのかについてですが，1つの理由として，期待値は確率変数の分布を理解するうえで有用な代表値だからです．もう1つの理由としては，期待値は予測誤差(MSE)を最小化できるからです(Angrist and Pischke, 2008, p.25)．通常，期待値が興味の対象ですが，中央値やパーセンタイルが興味の対象となる回帰分析もあります(quantile regression)． ↩︎
当たり前ですが， $E[U|X]=0$ が成り立たなければ，CEFは $E[Y|X] = \beta_0 + \beta_1 X + E[U | X]$ となり，誤差項の部分が残ったままになります．Zero conditional meanが満たされていないとき，誤差項は $X$ に依存するため， $X$ が1単位変化すると， $Y$ は $\frac{dY}{dX}=\beta_1 + \frac{dE[U|X]}{dX}$ 変化します．そうなると，単純なCEFのシステム $E[Y|X]=\beta_0 + \beta_1 X$ だけでは $X$ と $Y$ の因果関係はとらえきれず，係数 $\beta_1$ は因果効果として解釈できなくなります． ↩︎
サンプルの大きさは「サンプルサイズ」です．「サンプル数」という言葉はデータセットの数を意味し，複数回分析するとき以外は基本的に使いません． ↩︎
注意するべきこととして，モデルの推定方法を考える段階ではサンプルの分析単位は仮想的にに $i$ と置かれている状態で，まだ選ばれていません．よってここでの $(X_i, Y_i)$ はまだ実現値ではなく確率変数です．サンプルが実際のデータとして存在していれば，分析単位はすでに選ばれている状態なので(e.g. 個人 $i=1$ はAさん, 企業 $i=2$ はB社)，確率変数の実現値が観測されます(e.g. $x_{\text{Aさん}}=3個$ , $y_{\text{B社}}=1,000,000円$ )． ↩︎
誤差項 $U$ は観測されず推定で使えないので，さっさと代入で消去します． ↩︎
population moment conditions ↩︎
sample moment conditions ↩︎
母集団の真のパラメータ $\beta_0, \beta_1$ は誰も知りません．神のみぞ知る値です ↩︎
$\hat{\beta_1}$ は推定量(確率変数)を表すときもあれば，推定値(数値)を表すときもあります．推定方法を議論する段階でサンプルがまだ実際に選ばれていない状態 $(\hat{\beta_1}=確率変数の式)$ であれば推定量，観測されたデータを用いてパラメータの推定結果をもうすでに得ている状態 $(\hat{\beta_1}=数字)$ であれば推定値を意味します．この辺りはあまり違いを意識せずに表記している文献が多い印象です． ↩︎
分母が $X$ の分散なので，説明変数のデータの散らばりをもとにパラメータが推定されます．もし説明変数の散らばりがない( $X$ の値がみんな同じである)と，分母が $0$ となるので推定できなくなります． ↩︎
残差の表記は $U_i$ に $\hat{}$ を付けていますが，誤差項 $U_i$ とは異なるものです．誤差項は観測できませんが，残差はモデルの予測が現実のデータからどれだけ外れているかだけを意味しており，計算できます(予測が外れている原因はモデルに含まれていない誤差項 $U_i$ かもしれませんが)． ↩︎
全サンプルに対するモデルの予測パフォーマンスは，「二乗」の和でなくても測れます．例えば残差の「絶対値」の和でも予測精度は測れます．しかし，一般的には絶対値よりも二乗の方が後の計算が楽なので残差の二乗和が人気です．二乗和は予測が大きく外れたサンプルに対して大きいペナルティを課すことに留意しましょう． ↩︎
最小化問題なので $\sum_{i=1}^N (Y_i - \hat{\beta}_0 - \hat{\beta}_1 X_i)^2$ を $\hat{\beta}_0$ で(偏)微分するとゼロ ↩︎
OLSは仮定 $E[U|X]=0$ が満たされなければ，推定値は因果効果として信用できずにそこで終わります．一方MMのアイディアがあれば， $E[U|X]=0$ が満たされない場合でも新しいモーメント条件を加えることで $E[U|X]=0$ を満たすような新しい推定(e.g. IV)をデザインできます．OLS推定はMM推定の特殊ケースとして認識するといいでしょう． ↩︎
誤差項 $U$ はとりあえず標準正規分布に従うようにしましたが，正規分布である必要はありません．必要なのは $E[U|X]=0$ だけです． ↩︎
ここでは，奇跡的に母集団での $X$ と $Y$ の関係性(CEF, データ生成プロセス)を完璧にモデリングできたとします． ↩︎
サンプルサイズNを小さくしたらどうなるでしょうか？誤差項の分散σ_Uを大きくしたらどうなるでしょうか？シミュレーションではいろいろいじりながら勉強できるので楽しいですね． ↩︎
パッケージは通常行列でプログラムされているはずです． ↩︎
目に見えない能力は賃金に(正の)影響を与えそう，そして能力は教育とも(正に)相関しそう．妄想だけでも仮定が満たされない可能性があるので，今の分析の結果は信用できませんね． ↩︎