格子暗号を実装して格子基底簡約でさまざまな問題を解いてみる
この記事は暗号を理解して解読できるようになろうというシリーズの一部です。シリーズの一覧は次のようになっています。
格子とは
格子というのは基底を足し引きすることで現れる空間上に等間隔で並ぶ点の集合です。
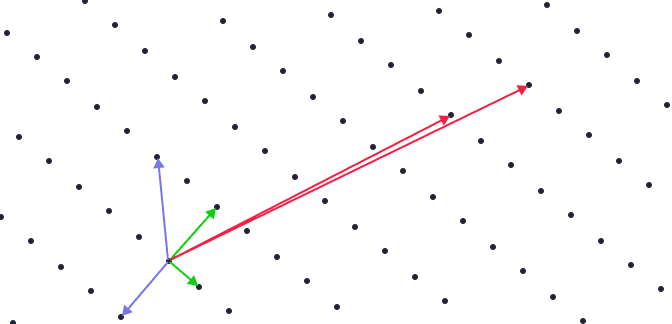
図では点をすべて集めたものを格子、同じ色の矢印が基底です。
例えば緑色の基底に注目してみましょう。これを 2 倍, 3 倍 ... とした基底を足し上げると全ての点を表現できます。こうしてみると格子っぽく見えますね。

同じように赤い基底でも同じ格子が作られますが、青い基底を張ってみると 1 つ飛ばしの格子が作られます。
なぜでしょうか?
これは基底を変換することでわかります。基底を変換するルールは毎回片方だけしか変更しないことです。
それでは青色の基底を変換してみましょう。
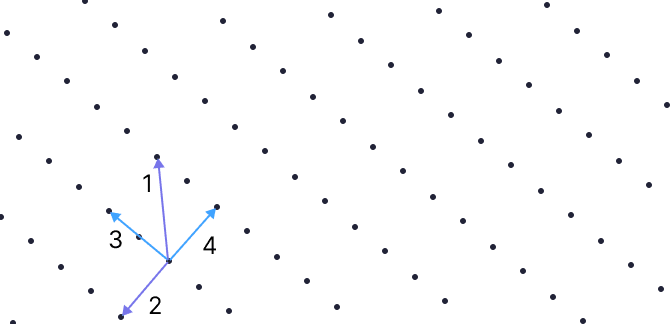
まず基底 1 に基底 2 を足すと矢印 3 になります。次に基底 2 を -1 倍すると矢印 4 になります。矢印 3, 4 を新しい基底とするとさっきの緑色の基底とを比べて一方の基底が 2 倍の長さになっています。だから 1 つ飛ばしの格子になるのです。
赤い基底の方も変換してみましょう。
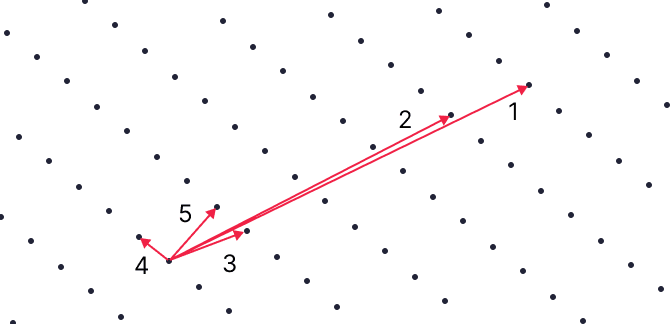
1 から 2 を引いて 3 になります。
2 から 3 の 4 倍を引いて 4 になります。
3 に 4 を足して 5 になります。
すると基底 4, 5 は緑色の基底と同じ格子を貼ることがわかります。
このように分かりにくかった基底を分かりやすい基底に変換する操作のことを基底簡約と言います。基底簡約することである点から最も近い距離の点を見つけ出すことが出来そうです。
とここまで矢印遊びをしてきましたが本質はもう語り尽くしました。これが格子の全てです。
格子の問題
これを数学的に表現すると次のように書けます。
Def. 格子
個の線形独立なベクトル n について整数係数の線形結合によって生成されるベクトルの集合を格子 \bm{b}_1,\ldots,\bm{b}_n\in\mathbb{R}^m と定義します。 \mathcal{L} \mathcal{L}(\bm{b}_1,\ldots, \bm{b}_n) := \left\lbrace\sum_{i=1}^{n} a_i\bm{b}_i\in\mathbb{R}^m\ \middle|\ a_i \in \mathbb{Z} \right\rbrace
先程の格子の基底の変換を基本変形と言います。
Prop.
格子基底の基本変形に対し、格子は不変である。
ここで原点から最短のベクトルを見つける問題を考えます。
SVP; Shortest Vector Problem
格子上の非零なベクトルの中で最もノルムが小さなベクトルを見つけ出す問題を SVP という。\bm{v} = v_1\bm{b}_1 + \cdots + v_n\bm{b}_n \qquad (v_1, \ldots , v_n \in \mathbb{Z}) \\
素朴に考えると最短ベクトルを見つける為には色んな係数を試して探索すれば良さそうですが、この方法だとベクトルの数に対して指数的に探索空間が広がるので計算時間も指数時間掛かります。この問題は NP 困難と知られていて、これをオーダーレベルで改善する方法は今のところ見つかっていません。また量子コンピュータでも効率的なアルゴリズムは見つかっていません。これが暗号で使われる全ての格子問題の基礎となります。ただ基底簡約によって最短ではないが最短に近いベクトルを見つける問題 (μSVP) を解くことはできます。次の章ではこの基底簡約アルゴリズムを紹介します。
基底簡約アルゴリズム
先程のように基底簡約するアルゴリズムはどのように組めば良いのでしょうか。
まず基底簡約で目指す基底を次のように定義します。
- それぞれの基底ベクトルが直交に近い状態
- 基底ベクトルの長さが短い
これを実現するアルゴリズムとして以下のようなものがあります。
今回は LLL 基底簡約アルゴリズムまでを扱います。それ以降のアルゴリズムは紹介しませんが、SageMath で使いはするので理解したければ参考文献を参考にしてください。
1 次元の格子 (ユークリッドの互除法)
2 つの整数を足し引きして最小となる値を求める。これは最大公約数を計算するのと同じで中学校でやったようにユークリッドの互除法を使うことで求められます。
例えば 390 と 273 についてユークリッドの互除法を考えると
ということから並べると 39 ずつ飛んだ点列となります。
2 次元の格子 (Lagrange 基底簡約)
ユークリッドの互除法を 2 次元格子に対して行ってみましょう。
Lagrange 基底簡約 (Gaussian Reduction)
となるように交換して \|\bm{v}_1\| < \|\bm{v}_2\| \bm{v}_2 \to \bm{v}_2 - \left\lfloor\frac{\bm{v}_1\cdot \bm{v}_2}{\|\bm{v}_1\|^2}\right\rceil\bm{v}_1 を繰り返し
となるとき m = 0 , \bm{v}_1 は最も簡約された基底となる。 \bm{v}_2
Theorem
Lagrange 簡約された基底は最も短い基底である。
Proof.
任意の非零ベクトル
これより 2 次元の格子も基底簡約が完了します。しかし 3 次元以上の格子では同様の方法で簡約しても最も短い基底とはならずに NP 困難な問題となります。この問題に立ち向かう為にはまず基底の直交性を高めることが必要です。
def gaussian_reduction(v1, v2):
while True:
if v2.norm() < v1.norm():
v1, v2 = v2, v1
m = floor(v1.dot_product(v2) / v1.dot_product(v1))
if m == 0:
break
v2 = v2 - m*v1
return v1, v2
v1 = vector([846835985, 9834798552])
v2 = vector([87502093, 123094980])
グラム・シュミット直交化
グラム・シュミット直交化 (GSO; Gram-Schmidt Orthonormalization) とはユークリッド空間で基底を直交基底に変換する方法です。図形的には
Def. GSO ベクトル
次元格子 n の順序付き基底 L\subseteq \mathbb{R}^m に対する GSO ベクトル \{\bm{b}_{1},\ldots, \bm{b}_{n}\} を GSO 係数 \bm{b}_{1}^* ,\ldots, \bm{b}_{n}^ *\in\mathbb{R}^m を用いて次のように定義する。 \mu_{i,j} \begin{aligned} &\begin{dcases} \bm{b}_1^* := \bm{b}_1 \\ \bm{b}_i^* := \bm{b}_i - \sum_{j=1}^{i-1} \mu_{ij} \bm{b}_j^* & (2\leq i\leq n) \\ \end{dcases} \\ &\quad \mu_{ij} := \frac{\langle \bm{b}_i, \bm{b}_j^* \rangle}{\| \bm{b}_j^*\|^2} \qquad (1\leq j<i\leq n) \end{aligned}
行列で書くと次のようになる。
これを
Thm. GSO ベクトルの基本性質
- 任意の
に対して 1\leq i<j\leq n が成り立つ。 \langle\bm{b}_i^*, \bm{b}_j^*\rangle = 0 - 任意の
に対して 1\leq i\leq n が成り立つ。 \|\bm{b}_i^*\|\leq\|\bm{b}_i\| - 任意の
に対して 1\leq i\leq n が成り立つ。 \langle\bm{b}_1^* ,\ldots,\bm{b}_i^*\rangle_{\mathbb{R}} = \langle\bm{b}_1,\ldots,\bm{b}_i\rangle_{\mathbb{R}} が成り立つ。 \mathrm{vol}(L) = \prod_{i=1}^n\|\bm{b}_i^*\|
Proof.
まず 1 について
が成り立つ。よって数学的帰納法より成り立つ。
2 に関しては定義式にノルムを取ることで分かる。
3 についてはまず
同様に
よって
4 については
より示される。
サイズ基底簡約
とりあえず GSO を用いて愚直にユークリッドの互除法を一般の格子に適用します。これをサイズ基底簡約と言います。
サイズ基底簡約
次元格子 n の基底 L を GSO 係数 \\{\bm{b_1},\ldots,\bm{b_n}\\} が \mu_{i,j} |\mu_{i,j}| \leq \frac{1}{2} \quad (1 \leq \forall j < \forall i \leq n) を満たすとき、基底
はサイズ簡約されているという。アルゴリズムとしては次のように行う。 \\{\bm{b_1},\ldots,\bm{b_n}\\}
として q = \lfloor\mu_{ij}\rceil と更新する。 \bm{b}_i\leftarrow\bm{b}_i - q\bm{b}_j - GSO 係数について
と更新する。 \mu_{il}\leftarrow \mu_{il} - q\mu_{jl}
def size_reduction(B):
n = B.nrows()
_, mu = B.gram_schmidt()
for i in range(n):
for j in range(i - 1, -1, -1):
if mu[i][j].abs() > 1 / 2:
q = mu[i][j].round()
B[i] -= q * B[j]
mu[i] -= q * mu[j]
return B
B = matrix([[5, -3, -7], [2, -7, -7], [3, -10, 0]])
print(B)
print(size_reduction(B))
LLL 基底簡約
LLL 基底簡約とは Lenstra 兄弟と Lovasz によって考案した効率の良い基底簡約のアルゴリズムです。これにはまず射影格子という概念を理解する必要があります。
Def. 射影格子
次元格子 n の基底 L\subseteq\mathbb{R}^m に対し, 各 \lbrace\bm{b}_1,\ldots, \bm{b}_n\rbrace に対して 1\leq l\leq n の直交補空間への直交射影を \langle\bm{b}_1,\ldots, \bm{b}_{l-1}\rangle_\mathbb{R} とする。GSO で示した定理から \pi_l:\mathbb{R}^m\to\langle\bm{b}_1,\ldots, \bm{b}_{l-1}\rangle_\mathbb{R}^\bot \begin{aligned} \langle\bm{b}_1, \ldots, \bm{b}_{l-1}\rangle_\mathbb{R}^\bot &= \langle\bm{b}_1^*, \ldots, \bm{b}_{l-1}^* \rangle_\mathbb{R}^\bot = \langle\bm{b}_l^*, \ldots, \bm{b}_n^* \rangle_\mathbb{R} \\ \pi_l(\bm{b}_i) &= \sum_{j=l}^i \mu_{i,j}\bm{b}_j^* \\ \end{aligned} となる。 すると集合
は \pi_l(L) を基底に持つ \lbrace\pi_l(\bm{b}_l), \ldots, \pi_l(\bm{b}_n)\rbrace 次元の格子であり, n-l+1 を射影格子 (projected lattice) と呼ぶ。 \pi_l(L)
言葉通り格子を射影してできる格子です。これを用いた Lovasz 条件を元に基底簡約するのが LLL 基底簡約です。
LLL (Lenstra-Lenstra-Lovasz) 基底簡約
Lovasz 条件をとしたときに任意の 1/4 < \delta < 1 に対して次を満たすこととする。 2\leq k\leq n \delta \|\bm{b}_{k-1}^*\|^2 \leq \|\pi_{k-1}(\bm{b}_k)\|^2 このとき次の 2 ステップを行えるまで繰り返す。
- サイズ基底簡約
- Lovasz 条件に合うように基底ベクトルの交換
Nguyen, Stehle らの研究などにより簡約された最小の基底の長さの上限は次の式程度に見積もられるらしいです。
def LLL(B, delta=0.99):
assert 1 / 4 < delta < 1
n = B.nrows()
b = [0 for _ in range(n)]
BB, mu = B.gram_schmidt()
i = 1
while i < n:
# size reduction
for j in range(i - 1, -1, -1):
if mu[i][j].abs() > 1 / 2:
q = mu[i][j].round()
B[i] -= q * B[j]
mu[i] -= q * mu[j]
b[i - 1] = BB[i - 1].dot_product(BB[i - 1])
b[i] = BB[i].dot_product(BB[i])
# Lovasz condition
if b[i] >= (delta - mu[i][i - 1] * mu[i][i - 1]) * b[i - 1]:
i += 1
else:
B.swap_rows(i - 1, i)
BB, mu = B.gram_schmidt()
i = max(i - 1, 1)
return B
B = [vector([5, -3, -7]), vector([2, -7, -7]), vector([3, -10, 0])]
print(LLL(B, 0.8))
より強い基底簡約アルゴリズム
CTF では LLL で十分簡約化できますが CVP を解く際に強いと取れるときがあるので知識として BKZ を知っておきましょう。
HKZ (Hermite-Korkine-Zolotareff) 基底簡約
- サイズ基底簡約
- すべての
に対して 1\leq i\leq n を満たすように基底ベクトルの交換 \|\bm{b}_i^*\| = \lambda_1(\pi_i(L))
BKZ (Block Korkine-Zolotareff) 基底簡約
- サイズ基底簡約
- すべての
に対して 1\leq k\leq n-\beta+1 次元の格子 \beta の基底を HKZ 基底簡約 L_{[k,k+\beta-1]} = \lbrace\pi_k(\bm{b}_k), \pi_k(\bm{b}_{k+1}), \ldots, \pi_k(\bm{b}_{k+\beta-1})\rbrace
基底簡約アルゴリズムの応用
多変数不定一次方程式の解
多変数不定一次方程式と言われてもパッと分からないと思いますが、こんな感じの方程式のことです。
例えば 2 変数のとき方程式は
しかし 3 変数以上だとユークリッドの互除法を応用するのが難しく代表解は求まりません。さてここで基底簡約の出番です。基底簡約アルゴリズムとはベクトルの足し引きをすることで小さなベクトルを見つけるアルゴリズムでした。これを方程式の足し引きに応用して格子問題に帰着させて解きます。
方程式
最後の行が
マジックみたいですがこれで本当に解けてしまいます。
M = matrix([
[1, 0, 0, 0, 0, 613],
[0, 1, 0, 0, 0, 1034],
[0, 0, 1, 0, 0, 1106],
[0, 0, 0, 1, 0, 857],
[0, 0, 0, 0, 1, 1302],
])
A = M.LLL()
print(A)
'''
[-3 1 -2 2 1 -1]
[ 0 -3 2 -2 2 0]
[-3 -1 3 1 -1 0]
[ 2 -1 1 0 -1 -4]
[ 2 -3 -1 5 -1 1]
'''
更に定数項を加えた方程式
を基底簡約して最後がゼロとなる行が見つかれば代表解が分かります!
ただし
また剰余の方程式
を基底簡約して最後がゼロとなる行を見つければいいです。
コストなしで何度でも
このように基底簡約アルゴリズムで多変数不定一次方程式を解くことができます。これらは CTF で頻出な技術です。次の良記事で練習するといいでしょう。
ナップサック暗号 (Markle-Hellman Knapsack encryption)
一般の数列
Def. 超増加列
次の性質を満たす数列を超増加列と呼ぶ。 \lbrace w_i\rbrace \sum_{i=1}^n w_i < w_{n+1}
ナップサック暗号 (Markle-Hellman Knapsack encryption)
鍵生成
- 超増加列
を生成する。 \lbrace w_i\rbrace - 整数
について q, r , q > \sum_i w_i なるように生成する。 \gcd(r, q) = 1 を計算し、 b_i = rw_i \pmod q を公開鍵、 \lbrace b_i\rbrace, q を秘密鍵とする。 \lbrace w_i\rbrace, r 暗号化
平文を用いて次のように暗号文 m_i\in\lbrace 0, 1\rbrace を得る。 c c = \sum_i m_ib_i \pmod q 復号
- 暗号文
に対して秘密鍵 c を用いて r を計算する。 c' = cr^{-1} \bmod q = \sum_i m_iw_i を降順に次のアルゴリズムを実行する。 i \begin{aligned} m_i & \leftarrow \begin{cases} 0 & (c' \leq w_i) \\ 1 & (c' > w_i) \end{cases} \\ c' & \leftarrow c' - w_i \end{aligned}
これが低密度のとき LLL を用いて攻撃する方法があります。LO 法 (Lagarias-Odlyzko Algorithm) と CLOS 法 (Coster LaMacchia Odlyzko Schnorr) と呼ばれています。
LO 法は次の行列を LLL 簡約して左端が
CLOS 法は基底行列をちょっと変更して精度を向上させた方法です。まず
Approximate Common Divisor Problem
数列に対して誤差を含む大枠の公約数を求めることも出来ます。
数列
この
Algorithms for the Approximate Common Divisor Problem
Coppersmith's Method
先ほど多変数不定一次方程式を考えましたが次に剰余上の
まず考えるのはそれぞれの次数について
これを改良する方法を考えます。まず剰余の方程式は係数がある程度小さければそのまま整数係数方程式となるよという主張をする Howgrave-Graham の補題を示します。
Lemma. Howgrave-Graham の補題
整数係数多項式について g(x) = g_0 + g_1x + g_2x^2 + \cdots + g_{d-1} x^{d-1} を法としたとき N を満たす解 |x_0| \leq X が整数係数多項式の解 g(x_0) = 0 \pmod{N} となる十分条件は次のようになる。 g(x_0) = 0 \|g(xX)\| = \sqrt{g_0^2 + (g_1X)^2 + (g_2X^2)^2 + \cdots + (g_{d-1}X^{d-1})^2} < \frac{N}{\sqrt{d}}
Proof.
剰余の方程式を基底簡約して係数を小さくすれば整数方程式に変換できて解けるのでは...!?と気付くでしょう。ただ基底簡約する為には同じ解を持つ複数の方程式が必要ですが今は 1 つしかありません。これに対しては剰余を
Lemma. Hensel の持ち上げ
多項式の解 f(x) に対して多項式 f(x_0) = 0 \pmod N が g_{i,j}(x) を満たすには次のようにおけばよい。 g_{i,j}(x_0) = 0 \pmod{N^m} g_{i,j}(x) := N^{m−i}x^j f^i(x) \qquad (0 \leq i \leq m, 0 \leq j\leq l) ただし
は整数とする。 m, l
Proof.
より
小さくしたい方程式は
ただし
これを基底簡約して出てきた方程式が Howgrave-Graham の補題の条件を満たしていれば整数係数方程式となって Berlekamp-Zassenhause 法などを用いて解けます。これらをまとめて Coppersmith Method と呼びます。
Thm. Coppersmith's Theorem
を f(x) を法とするモニックな N 次多項式について次の条件を満たすとき解 d ( x_0 ) を効率よく求めることができる。 |x_0| < X \|f(xX)\| < \frac{N}{\sqrt{d}}
条件式が覚えにくいので大体
さらに Coppersmith Method には拡張できることが 2 つあります。
- 未知の法について解ける
- 既知の法の約数を法とする式の解を求められます。約数の法が小さいほど方程式に対する制約がゆるくなります。
- 多変数の方程式も解ける
- 変数の数が多いほど方程式に対する制約がキツくなります。
これらは Howgrave-Graham の補題 などを見直すことで簡単に拡張できます。詳細は参考文献とかにあると思います。
理論としてはざっとこんな感じですが SageMath を使えば何も分からなくとも雰囲気で使えます。
Gröbner 基底
基底簡約の応用ではないですが似たようなものなのでここで紹介しておきます。
Gröbner 基底
多項式環におけるイデアル k[x_1,\ldots,x_n] の生成元 I において G の最高次の項がある f\in I の元の最高次の項の変数によって割り切れるような G を Gröbner 基底という。 G
このような Gröbner 基底は必ず存在します。少なくとも上の多項式環は Noether 環なので有限生成イデアルであることは分かります。最高次という言葉が出てきましたがこれは適切な順序付けによって必ず最大元が存在する、つまり全順序となっている必要があります。そのような順序付けは次のようなものがあります。
- 辞書式順序
- 次数辞書式順序
- 次数逆辞書式順序
そして簡約化によって Gröbner 基底を求められます。これもユークリッドの互除法を用います。
簡約化
イデアルの生成元に対して最高次の項の変数によって割り切れるような組 F が存在するならば割った余り f, g\in F に入れ替えるという操作をできるだけ繰り返す。 f \leftarrow f \bmod g
格子暗号
耐量子暗号の中では格子暗号が最も有力です。ただ耐量子性を示すのは難しいらしく、それを示せるような暗号が選考で通りがちらしいです。また格子の計算困難な問題にはさまざまな種類があり、それに応じてさまざまな格子暗号がありますが、今回は耐量子暗号や完全準同型暗号でよく使われる LWE 問題を紹介します。
最近ベクトル問題 (CVP)
LWE 問題を解く為にはまず CVP が解ける必要があります。SVP は原点に最も近い格子点を求める問題でしたが CVP はある点に最も近い格子点を求める問題です。
CVP; Closest Vector Problem
CVP とは目標ベクトル(格子点である必要はない) に対して格子上の最近ベクトル \bm{w} を求める問題である。 \bm{v}
厳密解を求めるのは難しいので近似解を求めます。この近似解を解く代表的な方法に Babai’s nearest plane algorithm と Kannan's embedding method があります。
Babai’s nearest plane algorithm
次元の格子について目標ベクトルに対して最も近い n 次元超平面を n-1 つ選ぶことを帰納的に繰り返すことで CVP を解く。 1
def babai_cvp(B, w):
n = B.nrows()
BB, _ = B.gram_schmidt()
e = w
for i in range(n)[::-1]:
c = (e.dot_product(BB[i]) / BB[i].dot_product(BB[i])).round()
e -= c * B[i]
return w - e
B = matrix([[1, 2, 3], [3, 0, -3], [3, -7, 3]])
w = vector([10, 6, 5])
v = babai_cvp(B, w)
print(v)
Kannan’s embedding method
CVP の目標ベクトルと解ベクトル w の差 v のノルムについて e = w - v が成り立つとき SVP を解くことで求まる。 \|e\| < \lambda_1/2
これは格子
を基底簡約して最も短いベクトルの行が解となります。
これは SVP より半分以上短い CVP の解があるから求まります。
def kannan_cvp(B, w):
n = B.nrows()
M = 1
BB = block_matrix([[B, matrix(ZZ, n, 1)], [w, M]])
BB = BB.LLL()
e = matrix(BB[0][0:n])
return w - e
B = matrix([[1, 2, 3], [3, 0, -3], [3, -7, 3]])
w = matrix([10, 6, 5])
v = kannan_cvp(B, w)
print(v)
Learning With Error
LWE 問題は機械学習理論から派生した求解困難な問題らしいです。LWE (Learning With Error) 問題を用いた暗号を LWE 格子暗号といいます。
LWE 問題
を体とする。 K を掛けて誤差ベクトル \bm{A}\in K^{m\times n}, \bm{s}\in K^m を与えた \bm{e}\in K^n に対し \bm{b}\in K^n が与えられたときに (\bm{A}, \bm{b}) を求める問題を一般に LWE (Learning With Error) 問題と呼ぶ。 \bm{s} \bm{A}\bm{s} + \bm{e} = \bm{b} 特に
を素数として q のとき LWE 問題、 K = \mathbb{F}_q かつ K = \mathbb{F}_q[x]/(x^n + 1) のとき Ring-LWE 問題、 m = 1 のとき Module-LWE 問題といいます。 K = \mathbb{F}_q[x]/(x^n + 1)
この誤差がなければ逆行列を掛ければすぐに求まるのですが、誤差があることで途端に問題が難しくなります。また
近似解は基底簡約して CVP として解く感じです。
def solve_LWE(A, b):
m = A.nrows()
n = A.ncols()
q = A.base_ring().order()
BB = block_matrix([[A.change_ring(ZZ).transpose()], [q * matrix.identity(m)]])
BB = BB.LLL()[n:]
v = babai_cvp(BB, b.change_ring(ZZ))
s = v[:n] * A[:n].transpose() ^ -1
return s
q = 29
A = matrix(
GF(q),
[
[1, 5, 21, 3, 14],
[17, 0, 12, 12, 13],
[12, 21, 15, 6, 6],
[4, 13, 24, 7, 16],
[20, 9, 22, 27, 8],
[19, 8, 19, 3, 1],
[18, 22, 4, 8, 18],
[6, 28, 9, 5, 18],
[10, 11, 19, 18, 21],
[28, 18, 24, 27, 20],
],
)
b = vector(GF(q), [28, 2, 24, 16, 11, 14, 7, 28, 27, 13])
s = solve_LWE(A, b)
print(s)
CRYSTALS-KYBER
CRYSTALS-KYBER とは NIST が選考している耐量子暗号の一種で Module-LWE を用いた暗号です。
簡単の為、
Def. 多項式の圧縮
またであれば各要素に対して圧縮を行う。 R_q
シード値から多項式を生成する関数 \rho を用いる。 Sam(\rho) \begin{aligned} \mathrm{Compress}_q(x, d) & = \lceil(2^d/q)x\rfloor \bmod q \\ \mathrm{Decompress}_q(x, d) & = \lceil(q/2^d)x\rfloor \end{aligned}
Prop. 圧縮解凍をしても誤差が小さい
として d < \lceil\log_2(q)\rceil と圧縮し、次のような性質を満たす。 \mathbb{F}_q\to\lbrace 0,\ldots,2^d-1\rbrace \begin{aligned} & x' = \mathrm{Decompress}_q(\mathrm{Compress}_q(x, d), d) \\ & |x' - x\bmod q|\leq\lceil q/2^{d+1}\rfloor \end{aligned}
これより圧縮解凍の誤差を LWE の誤差に乗せることができます。
CRYSTALS-KYBER
- 鍵生成
- 一様分布で
と二項分布で \bm{A}\in R_q^{k\times k} を生成し、 \bm{s}, \bm{e}\in R^{k} を計算する。 \bm{b} = \bm{A}\bm{s} + \bm{e} を圧縮したものを公開鍵、 (\bm{b}, \bm{A}) を秘密鍵とする。 \bm{s} - 暗号化
- 二項分布で
を生成する。 \bm{r}, \bm{e}_1\in R^k, e_2\in R を解凍して平文 \bm{b} を用いて m を圧縮したものを暗号文として返す。 (\bm{u}, v) = (\bm{A}^T\bm{r} + \bm{e}_1, \bm{b}^T\bm{r} + e_2 + \lceil\frac{q}{2}\rfloor \cdot m) - 復号
暗号文を解凍して (\bm{u}, v) 、つまり \mathrm{Compress}_q(v - \bm{s}^T\bm{u}, 1) に近い値は q / 2 、 1 に近い値は 0 として返す。 0
from Crypto.Util.number import bytes_to_long
from Crypto.Random.random import randint, getrandbits
def num2bins(x):
y = []
while x != 0:
y.append(x & 1)
x >>= 1
return y
def bins2num(x):
y = 0
for i in range(len(x)):
y += x[i] * (1 << i)
return y
class CrystalsKyber:
def binomial_poly(self):
res = []
for i in range(self.N):
tmp = 0
for i in range(self.eta):
a = getrandbits(1)
b = getrandbits(1)
tmp += a - b
res.append(tmp)
return self.Rq(res)
def random_poly(self):
return self.Rq([randint(int(0), int(self.q)) for _ in range(self.N)])
def __init__(self, q, k, eta, N):
K = GF(q)
PR.<X> = GF(q)[]
Rq.<x> = PR.quotient(X^N + 1)
self.Rq = Rq
self.q = q
self.k = k
self.eta = eta
self.N = N
A = matrix([[self.random_poly() for _ in range(k)] for _ in range(k)])
s = vector([self.binomial_poly() for _ in range(k)])
e = vector([self.binomial_poly() for _ in range(k)])
b = A * s + e
self.pub = (b, A)
self.priv = s
def encrypt(self, m):
Rq.<x> = self.Rq
(b, A) = self.pub
m = Rq(num2bins(m))
r = vector([self.binomial_poly() for _ in range(self.k)])
e1 = vector([self.binomial_poly() for _ in range(self.k)])
e2 = self.binomial_poly()
u = A.transpose() * r + e1
v = b * r + e2 + (q / 2).round() * m
return (u, v)
def decrypt(self, c):
s = self.priv
u, v = c
m = v - s * u
ms = []
# 1 if the coeff is close to q / 2
for coeff in m.lift().coefficients(sparse=False):
coeff = QQ(coeff) * 2 / q
coeff = coeff.round() % 2
ms.append(coeff)
return bins2num(ms)
q, k, eta, N = 7681, 3, 4, 256
enc = CrystalsKyber(q, k, eta, N)
m = 11
assert m < 2^N
c = enc.encrypt(m)
_m = enc.decrypt(c)
assert m == _m
どのくらいの情報があれば LWE の暗号を破れるのかは Too Many Hints – When LLL Breaks LWE を読むといいでしょう。
まとめ
格子の基底簡約アルゴリズムは格子暗号だけではなく様々な暗号の攻撃に応用でき、CTF では非常に重要なツールとなります。これが出来るようになれば Crypto 上級者の仲間入りなんじゃないでしょうか。
Discussion