楕円曲線暗号を実装して有名な攻撃を試してみる
この記事は暗号を理解して解読できるようになろうというシリーズの一部です。シリーズの一覧は次のようになっています。
今回紹介するのは楕円曲線暗号です。
楕円曲線の理論は本来、群環体、ガロア理論、可換環論、ホモロジー代数、代数幾何学と理解した先で学習しますが、記事で書くには重すぎるので、高校数学だけで出来る限り紹介します。ただどうしようもないときにはちゃんと定義せずに代数幾何の言葉を使うと思うのでそこはすみません。
楕円曲線
高校のときに習ったと思いますが、グラフで半径 1 の円といえば次のような式で表されました。
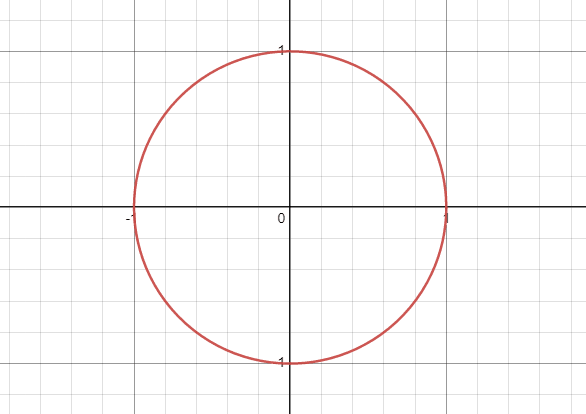
楕円曲線は言うなればこの 3 次方程式バージョンです。
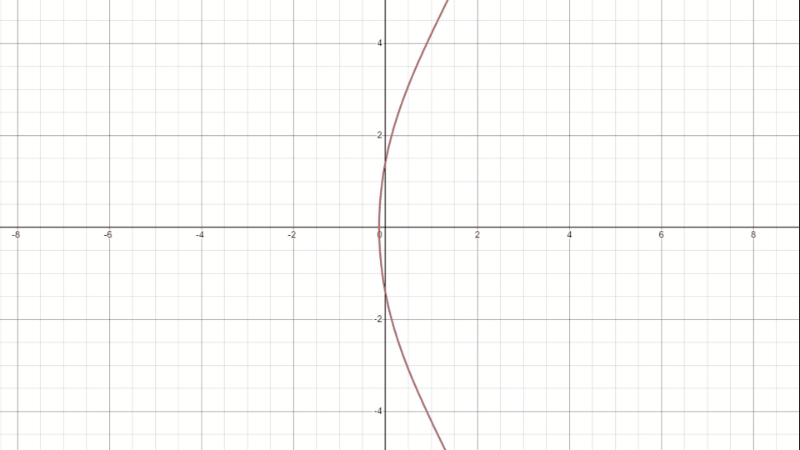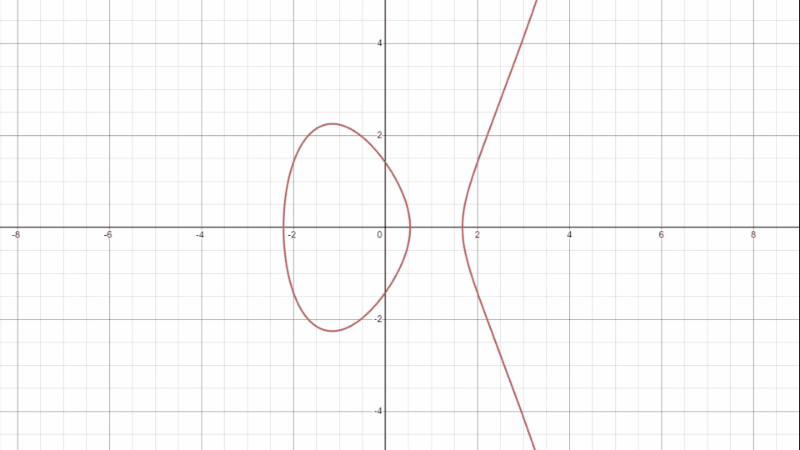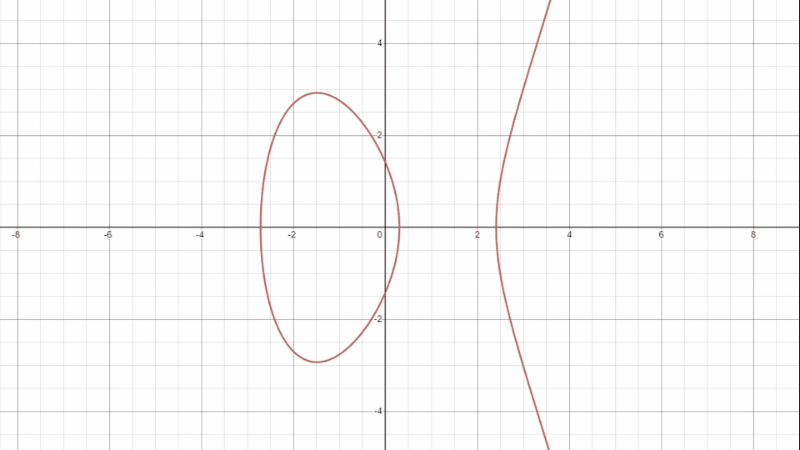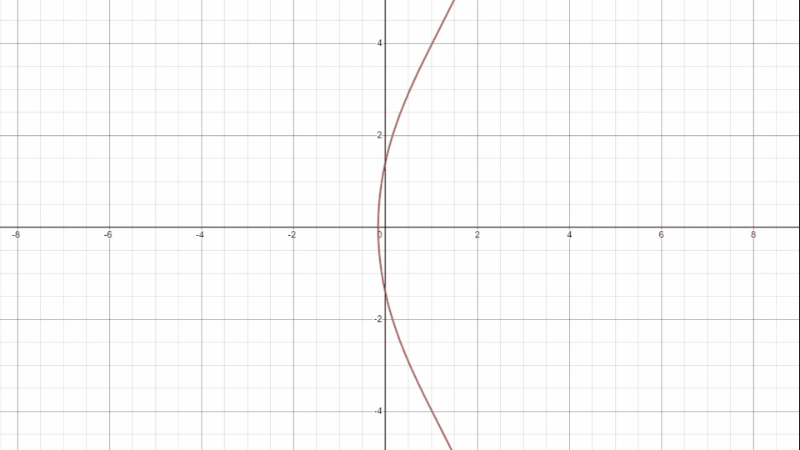
グラフがどうしてこんな形になるかというと、まず楕円曲線を
この章では楕円曲線の点同士で行われる摩訶不思議な"足し算"を紹介します。
一般の楕円曲線の定義
まずは楕円曲線の定義をちゃんと行います。読み飛ばしても構いません。
Def.
体に対して次の方程式 (Weierstrass 方程式) の解の集合を楕円曲線といい、記号としては K や E/K や E(K) を略して K とも書く. E y^2 + a_1xy + a_3y = x^3 + a_2x^2 + a_4x + a_6
体とは四則演算ができる代数構造です。実数
Prop.
体の標数が K でないとき 2, 3 の線形変換によって 2 次項を消すことができ、 x, y を用いて次のように書ける。 a, b\in K y^2 = x^3 + ax + b
体の標数
Proof.
さらに
こうして Weierstrass 方程式は標数が 2, 3 ではないとき
以下では特に断りがない限り標数が 2, 3 ではない有限体上の楕円曲線を扱います。
楕円曲線の和
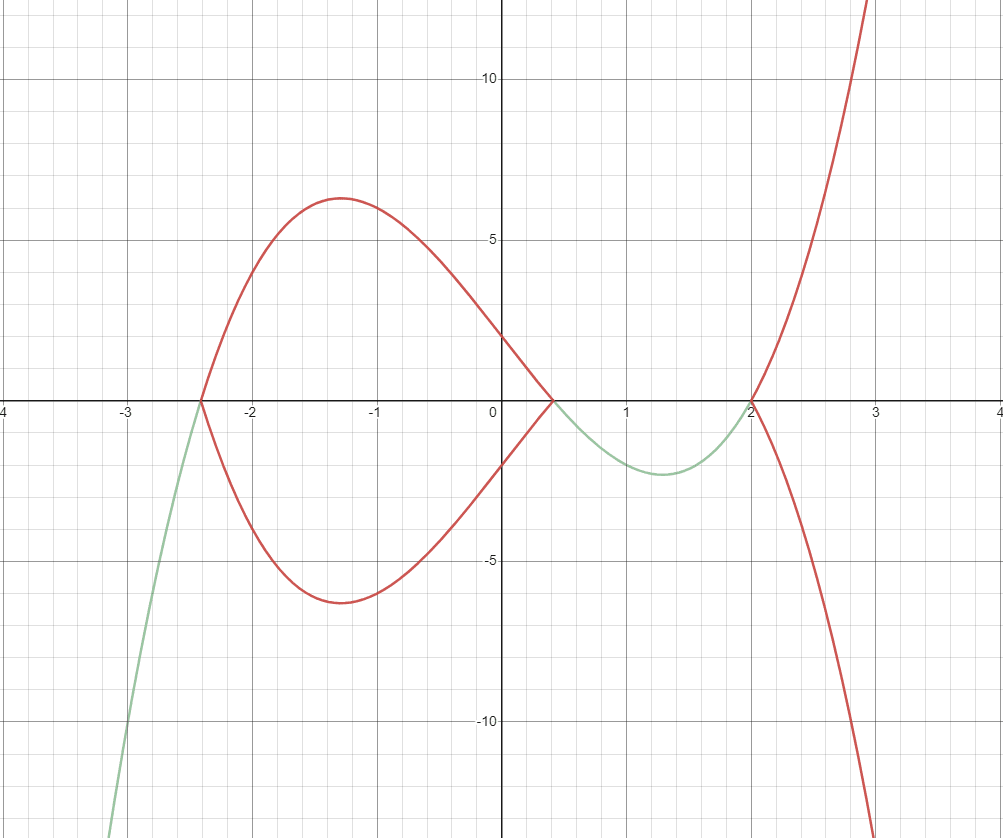
そしてここから本題に入るのですが、この楕円曲線上にある点同士で足し算ができます。
Def. 楕円曲線上の和
楕円曲線上の点同士の和の群 E を次のように定義する。 (E, +)
- 単位元を無限遠点
とする。 \mathcal{O} - 点
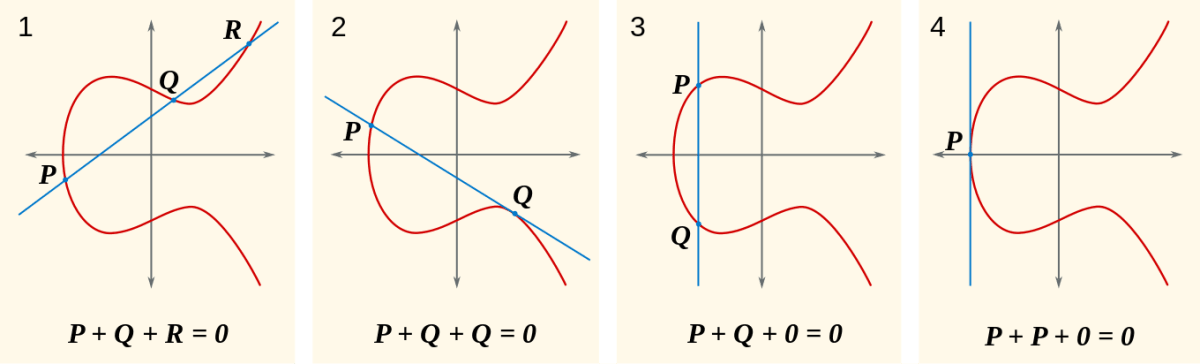
の逆元を P = (x, y) とする。 -P = (x, -y) に対して P(x_1, y_1), Q(x_2, y_2) を次のように定義する。 R(x_3, y_3) = P + Q \begin{aligned} x_3 &= \lambda^2 - x_1 - x_2 \\ y_3 &= \lambda(x_1 - x_3) - y_1 \\ \lambda &= \begin{dcases} \frac{y_2 - y_1}{x_2 - x_1} \quad (P \neq Q) \\ \frac{3x_1^2 + a}{2y_1} \quad (P = Q) \end{dcases} \end{aligned}
定義の式自体はぱっと見不自然と感じる人が多いと思うのですが幾何的に見ると自然となっていて、楕円曲線上の点
例えば次の楕円曲線
よって
このような具体例は次のサイトが分かりやすいと思います。
楕円曲線の位数
位数は楕円曲線の性質を解き明かす上で とてもとても重要 です。
Def. 楕円曲線の位数と楕円曲線上の点の位数
楕円曲線の位数とは楕円曲線上の点の個数、楕円曲線上の点の位数とは P となる最小の自然数 nP = \mathcal{O} です。 n
Def. ねじれ群
楕円曲線の点 E について P 倍したら単位元 n となるとき \mathcal{O} を P -等分点といい、 n -等分点の集合を n -ねじれ群 n という。 E[n] E[n] = \lbrace P\in E(\mathbb{F}_q) \mid nP = \mathcal{O}\rbrace
その楕円曲線の位数に関して最も重要な定理があります。
Thm. Hasse の定理
楕円曲線の位数 E/\mathbb{F}_q について次の条件で押さえられる。 \#E(\mathbb{F}_q) |\#E(\mathbb{F}_q) - (q+1)|\leq 2\sqrt{q}
Sketch.
ここでは標数が 2, 3 ではないときの証明の筋書きだけ記します。詳しくは Hasse's Theorem on Elliptic Curves をご覧ください。
まずベースとなる楕円曲線
次に
これらは同型写像
これらを用いて点
例えば
この
よって
実際に楕円曲線の位数をプロットしてみると
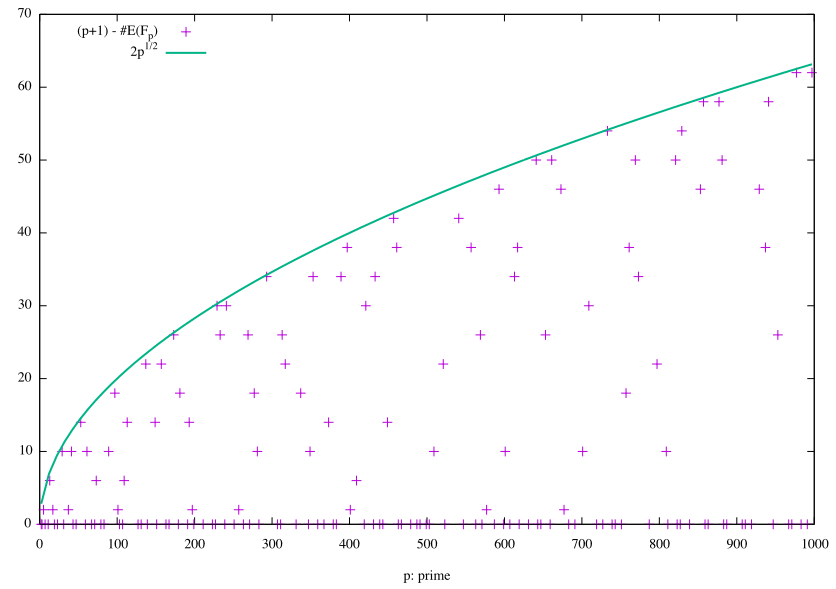
tsujimotterのノートブック - 楕円曲線のハッセの定理 より
次は実際に位数を計算する方法を考えます。
ただし楕円曲線のパラメータを用いた一般的な位数の表式については 未解決問題 となっています。ここではアルゴリズムで実験的に求めるという方法で求めます。
ところで有限体の重要な性質の 1 つにフロベニウス写像という重要な準同型写像の存在があります。これは楕円曲線にもあって、その性質の一つであるフロベニウス写像の特性多項式は位数を求めるときに重宝します。
Def. 楕円曲線におけるフロベニウス写像
楕円曲線におけるフロベニウス写像 E/\mathbb{F}_q を次のように定義する。 \phi \phi: (x, y)\mapsto (x^q, y^q) 楕円曲線
のフロベニウス写像を E/\mathbb{F}_q として \phi とおくと次の式が成り立つ。これをフロベニウス写像の特性多項式という。 t = \#E(\mathbb{F}_q) - (q+1) \phi^2 - t\phi + q = 0
この
実際に特性多項式に楕円曲線の点
Hasse の定理より
Schoof のアルゴリズム
楕円曲線の位数 E/\mathbb{F}_q を \#E(\mathbb{F}_q) で求められる。 O(\log^8q)
Proof.
これに小さな素数
右辺を計算し、左辺について
今回はフロベニウス写像の特性多項式を使いましたが、モジュラー多項式を使うことで
これで位数を求めることができるようになりました!それでは楕円曲線暗号の説明について早速入っていきましょう。
class ElipticCurveOverFp:
"""
y^2 = x^3 + ax + b (mod p)
"""
def __init__(self, a, b, p):
self.Fp = GF(p)
self.a = self.Fp(a)
self.b = self.Fp(b)
self.p = p
class Point:
def __init__(self, curve: ElipticCurveOverFp, x, y, infty=False):
self.x = curve.Fp(x)
self.y = curve.Fp(y)
self.curve = curve
self.infty = infty
if self.y**2 != self.x**3 + self.curve.a * self.x + self.curve.b and not self.infty:
raise ValueError(f"Invalid point, x:{x}, y:{y} is not on the curve")
@staticmethod
def infinity(curve: ElipticCurveOverFp) -> "Point":
return Point(curve, 0, 0, True)
def is_infinity(self) -> bool:
return self.infty
def __add__(self, other) -> "Point":
if self.is_infinity():
return other
if other.is_infinity():
return self
if self.x == other.x and self.y == -other.y:
return Point.infinity(self.curve)
if self.x == other.x and self.y == other.y:
lambda = (3 * (self.x**2) + self.curve.a) / (2 * self.y)
else:
lambda = (other.y - self.y) / (other.x - self.x)
x = lambda**2 - self.x - other.x
y = lambda * (self.x - x) - self.y
return Point(self.curve, x, y)
def __rmul__(self, n: int) -> "Point":
temp = self
res = Point.infinity(self.curve)
while n > 0:
if n & 1 == 1:
res += temp
temp += temp
n >>= 1
return res
楕円曲線暗号
楕円曲線暗号 (ECC) は RSA 暗号と同時期に開発された暗号で 1985 年頃に Victor S. Miller と Neal Koblitz が同時期かつ独立に発明しました(ちなみに Miller-Rabin 素数判定法の Miller は Gary L. Miller で別人です)。特徴としては RSA 暗号よりも純粋に強い暗号であることや鍵長が短いことなどが挙げられます。
さて、ここでこの楕円曲線上の加法を用いた次のような問題を作れます。
楕円曲線上の離散対数問題 (ECDLP : Elliptic Curve Discrete Logarithm Problem)
楕円曲線上の点に P, Q という関係があるとき Q = dP を求めよ。 d
つまり楕円曲線の世界で「割り算」をしなさいという問題です。
実はこの問題はとても難しく、これを解く効率的なアルゴリズムは現在見つかっていません。この ECDLP を利用して暗号の形にしたものが楕円曲線暗号です。楕円曲線暗号の例としては ECDH があります。
楕円曲線暗号による鍵共有
公開鍵暗号を用いて鍵を直接共有することなく共有鍵を構築する方法の一つにディフィーヘルマン鍵共有があります。その中で ECDLP (正確には ECDHH) を安全性根拠とするものを楕円曲線ディフィーヘルマン鍵共有 (ECDH; Elliptic Curve Diffie–Hellman key exchange) と呼びます。
楕円曲線ディフィーヘルマン鍵共有 (ECDH)
- セットアップ
楕円曲線とベースポイント E/\mathbb{F}_p を共有する P\in E/\mathbb{F}_p - 鍵生成
Alice と Bob はそれぞれ疑似乱数を生成し、 d_A, d_B を秘密鍵、 d_A, d_B を公開鍵として公開する Q_A = d_AP, Q_B = d_BP - 鍵交換
Alice と Bob は自分の秘密鍵と相手の公開鍵を掛けるととなり、 S = d_Ad_BP = d_AQ_B = d_BQ_A の S 座標をハッシュ化したものが Alice と Bob のみが知る共通鍵となる x
このように攻撃者は
楕円曲線暗号による電子署名
ECDLP を安全性根拠とする電子署名もあります。
ECDSA
- セットアップ
楕円曲線とベースポイント E/\mathbb{F}_p を共有する P\in E/\mathbb{F}_p - 署名
秘密鍵と公開鍵 d を生成し、平文のハッシュ値 Q = dP, k に対して m と計算し r = (kP)_x, s = (m + rd)k^{-1} を署名とする (r, s) - 検証
について (x, y) = ms^{-1}G + rs^{-1}Q となることを検査する x = r
楕円曲線暗号のパラメータ
暗号標準を定める国際機関によって楕円曲線のパラメータが決まっています。規格化された楕円曲線のパラメータの情報がすべてまとまっている資料があります。これは適当にパラパラめくるだけで面白いです。
また、より高速化させる為に様々な楕円曲線が考案されています。ただ 1 回の和に必要な演算が数回変わるだけでオーダーレベルでは変わらないので詳細は省きます。
| モデル | 式 | 座標 |
|---|---|---|
| ワイエルシュトラス | ||
| モンゴメリー | ||
| エドワード | ||
| ねじれエドワード | ||
| ハフ | ||
| ヤコビ交差 |
ECDLP を解く
計算機代数の章で紹介する DLP を解く方法を楕円曲線に適用すればよいだけです。ここでは Baby-step Giant-step と
Baby-step Giant-step
楕円曲線
これより計算量は
Pollard's rho 法
各点の係数を
これは誕生日のパラドックスによって
Pohlig-Hellman
中国剰余定理を用いて大きな群を複数の小さな群の直積に分けます。楕円曲線暗号の楕円曲線の位数は細かく素因数分解できることが多いので RSA とかと違って実用的な手法になります。
Pohlig-Hellman
楕円曲線の位数がと素因数分解できるとき \#E = p_1^{e_1}p_2^{e_2}\ldots p_k^{e_k} で ECDLP が解ける。 \mathcal{O}\left(e_i\sqrt{p_i}\right)
これより次の関係式が成り立つ。
この
これより ECDLP を解くことで
def pohlig_hellman(G):
fact = factor(G.order())
order = int(G.order())
dlogs = []
primes = []
for p, e in fact:
t = order // p ^ e
dlog = discrete_log(t * Q, t * G, operation="+")
dlogs.append(dlog)
primes.append(p ^ e)
return crt(dlogs, primes)
Index Calculus Algorithm
楕円曲線上の DLP を Index Calculus Algorithm で解く試みは歴史が長く、以下のようなことがありました。
| 手法 | 著者 | 説明 |
|---|---|---|
| Index Calculus | 1991: Adleman-DeMarrais-Huang 1997: Gaudry |
種数の大きい超楕円曲線上の DLP を Index Calculus Algorithm で解く |
| Weil descent | 1998: Frey |
|
| Generalized Weil descent | 2004: Gaudry-Hess-Smart 2007: Nagao |
|
ここでは Generalized Weil descent を紹介しようと思います。
Index Calculus Algorithm
- 因子基底
を作る。 B = \lbrace P\in E(\mathbb{F}_{p^k})\mid P_x\in\mathbb{F}_p\rbrace = \lbrace B_1,\ldots,B_n\rbrace - 次の関係式を与える。
r_iP = \sum_{j=1}^n e_{ij}B_j
- 行列で書くと次のようになるので
を求める。 \log_P B_j \begin{pmatrix} r_1 \\ \vdots \\ r_n \end{pmatrix} = \begin{pmatrix} e_{11} & \cdots & e_{1n} \\ \vdots & \ddots & \vdots \\ e_{n1} & \cdots & e_{nn} \end{pmatrix} \begin{pmatrix} \log_P B_1 \\ \vdots \\ \log_P B_n \end{pmatrix}
- 再び次の関係式を与えることで DLP が解ける。
\begin{aligned} Q + rP &= \sum_{j=1}^n e_jB_j \\ Q &= \sum_{j=1}^n (e_j\log_P B_j)P - rP \\ \end{aligned}
ここで関係式を見つける方法が最も重要です。Gaudry は Semaev の Summation polynomials を用いて関係式を見つけています。
Thm. Semaev の Summation polynomials
楕円曲線において E/k 変数多項式 n が存在し、次の S_n(x_1,\ldots,x_n)\in k[x_1,\ldots,x_n] に対して次の式が成り立つ。 P_i = (X_i, Y_i)\in E/k \exists s_i = \pm 1\quad s_1P_1 + \cdots + s_nP_n = 0 \iff S_n(X_1,\ldots,X_n) = 0
のとき E:y^2 = 4x^3 + ax + b は次の漸化式が成り立つ。 S_n(x_1,\ldots,x_n) \begin{aligned} S_2(x_1, x_2) & = x_1 - x_2 \\ S_3(x_1,x_2,x_3) & = (x_1 - x_2)^2x_3^2 - 2\left((x_1 + x_2)\left(\frac{a}{4} + x_1x_2\right) + \frac{b}{2}\right)x_3 \\ & + \left(x_1x_2 - \frac{a}{4}\right) - b(x_1 + x_2) \\ S_n(x_1,\ldots,x_n) & = \mathrm{Res}_x(S_j(x_1,\ldots,x_{j-1}, x), S_{n-j+2}(x_j,\ldots,x_n,x)) \end{aligned}
Gaudry のアルゴリズム
の E/\mathbb{F}_{p^3} y^2 = x^3 + ax + b を解くことを考える。 (a\in\mathbb{F}_p, b\in\mathbb{F}_{p^3}) の因子を Q として B_i = (X_i, Y_i) とおくと \mathbb{F}_{p^3} = \mathbb{F}_p[t]/(f(t)) \begin{aligned} & Q + B_1 + B_2 + B_3 = 0 \\ \iff & S_4(X_1, X_2, X_3, x) = \phi_0(X_1, X_2, X_3) + \phi_1(X_1, X_2, X_3)t + \phi_2(X_1, X_2, X_3)t^2 = 0 \\ \iff & \phi_0(X_1, X_2, X_3) = 0, \phi_1(X_1, X_2, X_3) = 0, \phi_2(X_1, X_2, X_3) = 0 \end{aligned} より 3 つの代数方程式が得られるので Gröbner 基底を計算することで
が求まる。 X_1, X_2, X_3
この計算量は
攻撃手法
この ECDLP を解くことができれば ECDH を含め、様々な楕円曲線暗号を解くことができます。さて主に攻撃対象となる楕円曲線暗号は以下のようなものがあります。
| アンチケース | 攻撃名 | 方法 |
|---|---|---|
| なし | ECDLP | 単純に ECDLP を解く |
| 位数が Smooth number |
Pohlig Hellman Attack | 位数 |
| Anomalous な曲線 |
SSSA Attack |
|
| Supersingular な曲線 |
MOV / FR Reduction | 埋め込み次数 |
| Singular な曲線 |
Singular Curve Point Decompression Attack |
|
| 楕円曲線上に存在しない点や位数の少ない点を指定できる | Invalid Curve Attack / Small-Subgroup Attack | さまざまな少ない位数の点を収集して中国剰余定理 |
楕円曲線上に存在しない点や位数の少ない点を指定できてはいけない (Invalid Curve Attack / Small-Subgroup Attack)
楕円曲線に乗らない点を乗っているように演算すると位数の小さい点となります。これを理解する為にもう一度楕円曲線上の和について復習しましょう。
Def. 楕円曲線上の和
楕円曲線上の点同士の和の群 E を次のように定義する。 (E, +)
- 単位元を無限遠点
とする。 \mathcal{O} - 点
の逆元を P = (x, y) とする。 -P = (x, -y) に対して P(x_1, y_1), Q(x_2, y_2) を次のように定義する。 R(x_3, y_3) = P + Q \begin{aligned} x_3 &= \lambda^2 - x_1 - x_2 \\ y_3 &= \lambda(x_1 - x_3) - y_1 \\ \lambda &= \begin{dcases} \frac{y_2 - y_1}{x_2 - x_1} \quad (P \neq Q) \\ \frac{3x_1^2 + a}{2y_1} \quad (P = Q) \end{dcases} \end{aligned}
この定義をよく見てみると
Singular な曲線を用いてはいけない (Singular Curve Point Decompression Attack)
特異点を持つ楕円曲線は写像を通して FFDLP に落ちます。
Def. 特異点
ある関数の特異点とは次を満たす点 f(x, y) = 0 である。 (X, Y) \left.\frac{\partial f}{\partial x}\right|_{(X, Y)} = \left.\frac{\partial f}{\partial y}\right|_{(X, Y)} = 0
このように微分値が不定となる点、グラフ上では関数の曲線が交差している点を特異点と言います。楕円曲線では次のように計算できます。
これより楕円曲線の特異点が存在すれば
楕円曲線の曲線は高々 1 回交わることになるので 2 つのタイプに分けられます。1 つは十字に交わるノード、もう 1 つは接しながら交わるカスプです。
カスプの場合
どんな尖っている楕円曲線も平行移動や線形変換により
ノードの場合
より特異点が原点しかないことがわかります。このとき
def SingularCusp(a, b, p):
PR.<x> = GF(p)[]
E = x^3 + a*x + b
roots = E.roots()
dx = next(filter(lambda x: x[1] == 3, roots))[0]
dy = 0
def f(P):
if P == 0:
return 0
x, y = P[0], P[1]
return x / y
g = f((gx - dx, gy - dy))
p = f((px - dx, py - dy))
return p / g
def SingularNode(a, b, p):
PR.<x> = GF(p)[]
E = x^3 + a*x + b
roots = E.roots()
dx = next(filter(lambda x: x[1] == 2, roots))[0]
dy = 0
E_ = E.subs(x = x + dx)
roots = E_.roots()
k = next(filter(lambda x: x[1] == 1, roots))[0]
k = (-k).square_root()
def f(P):
if P == 0:
return 1
x, y = P[0], P[1]
return (y + k * x) / (y - k * x)
g = f((gx - dx, gy - dy))
p = f((px - dx, py - dy))
return p.log(g)
Anomalous な曲線を用いてはいけない (SSSA Attack)
位数が
このとき次の関数
ただし還元写像
このとき次の定理が成り立ちます。
Thm.
が零写像ではないとき点 \lambda_E に対して次のようになる。 P\neq \mathcal{O} \lambda_E(P) = -\frac{x_{p-1} - x_1}{p(y_{p-1} - y_1)}\in\mathbb{Z}_p^\times ただし
とする。 u(nP) = (x_n, y_n)\in E(\mathbb{Q}_p)
Proof.
まず
と矛盾するので
これより
ここで
ここで
この手法をまとめると次のように計算することで DLP は
-
A = \pi(P) \bmod p^2 = (x_1, y_1)\in E(\mathbb{Z}/p^2\mathbb{Z}) -
(p-1)A = (x_{p-1}, y_{p-1})\in E(\mathbb{Z}/p^2\mathbb{Z}) -
x_{p-1} \neq x_1 \lambda_E(P) = 0 \lambda_E(P) = \dfrac{x_{p-1} - x_1}{p(y_{p-1} - y_1)} - そして
d = \dfrac{\lambda_E(Q)}{\lambda_E(P)}
def hensel_lift(E, P):
p = E.base_ring().order()
a, b = map(ZZ, [E.a4(), E.a6()])
x, y = map(ZZ, P.xy())
s = (x^3 + a*x + b - y^2) // p
s = lift(GF(p)(s) / (2*y))
return (x, y + p * s)
def lambda_E(E, P):
p = E.base_ring().order()
x1, y1 = P.xy()
xp_1, yp_1 = ((p - 1) * P).xy()
res = Zmod(p^2)(ZZ(xp_1 - x1) / p) / (yp_1 - y1)
assert res != 0
return res
def SSSA_attack(E, P, Q):
p = E.base_ring().order()
a, b = E.a4(), E.a6()
assert E.cardinality() == p
assert E.trace_of_frobenius() == 1
Px, Py = P = hensel_lift(E, P)
Qx, Qy = Q = hensel_lift(E, Q)
A = ((Qy^2 - Py^2) - (Qx^3 - Px^3)) / (Qx - Px)
B = Py^2 - Px^3 - int(a)*Px
R = Zmod(p^2)
lE = EllipticCurve(R, [A, B])
P, Q = lE(P), lE(Q)
return lambda_E(E, P) / lambda_E(E, Q)
Supersingular な曲線を用いてはならない (MOV / FR Reduction)
位数が
Def. 双線形写像 (Bilinear map)
群について写像 G_1, G_2 が次を満たすとき、 f: G_1\times G_1\to G_2 を双線形写像あるいはペアリングという。 f \begin{aligned} f(x_1x_2, y) = f(x_1, y)f(x_2, y) \\ f(x, y_1y_2) = f(x, y_1)f(x, y_2) \end{aligned}
楕円曲線暗号では Weil pairing や Tate pairing などのペアリングを使いますが、これらのペアリングは因子 (divisor) と呼ばれる概念を通じて理解します。この因子を求めるアルゴリズムを Miller's algorithm といいます。
Miller's algorithm
h_{P, Q}(x, y) = \begin{dcases} \frac{y - y_P - \lambda(x - x_P)}{x + x_P + x_Q - \lambda^2 - a_1\lambda + a_2} & (\lambda\neq\infty) \\ x - x_P & (\lambda = \infty) \end{dcases}
def h(P, Q, R):
if (P == Q and P.y == 0) or (P != Q and P.x == Q.x):
return R.x - P.x
L = P.line_coeff(Q)
p = R.y - P.y - L * (R.x - P.x)
q = R.x + P.x + Q.x - L * L
return p / q
def miller(P, Q, m):
if P == Q:
return 1
f = 1
T = P
for i in reversed(m.bits()):
f = f * f * h(T, T, Q)
T = T + T
if i == 1:
f = f * h(T, P, Q)
T = T + P
return f
Weil pairing
Miller's algorithm で得た因子から得られる f_P, f_Q を Weil pairing という。 e_m: E[m]\times E[m] \to \mu_m\subseteq\mathbb{F}_{p^k}^\times e_m(P, Q) = \frac{f_P(Q + S)}{f_P(S)}\bigg/\frac{f_Q(P - S)}{f_Q(-S)} Weil pairing は次の条件を満たす。
- 双線形 (bilinear)
双線形写像である。- 同一性 (idenntity)
e_n(P, P) = 1 - 非退化 (non-degenerate)
任意のに対して Q\in E[n] ならば e_n(P, Q) = 1 である。 P = \mathcal{O}
def weil_pairing(E, P, Q, m, S=None):
if S is None:
S = E.random_point()
fpqs = miller(P, Q + S, m)
fps = miller(P, S, m)
fqps = miller(Q, P - S, m)
fqs = miller(Q, -S, m)
return (fpqs / fps) / (fqps / fqs)
def tate_pairing(E, P, Q, m, k=2):
f = miller(P, Q, m)
return f ^ ((p ^ k - 1) // m)
埋め込み次数
必要となる最小の拡大次数を埋め込み次数という。 d
特に超特異楕円曲線において埋め込み次数は小さくなります。
Prop.
Supersingular な楕円曲線の埋め込み次数は以下である。 6
Proof.
これより Supersingular な楕円曲線上の ECDLP でペアリングを通すことで FFDLP に変換できる。
MOV / FR Reduction
ペアリングとおいて次のように計算する。 e_n
となる最小の E[n]\subseteq E(\mathbb{F}_{p^k}) を得る k - 位数
の n となるような \alpha = e_n(P, S), \beta = e_n(Q, S) を取る S\in E[n] に対して \alpha, \beta の FFDLP を解く \mathbb{F}_{p^k}^\times これに関してペアリングの種類によって名前が異なる。
- Weil pairing を用いるものを MOV (Menezes-Okamoto-Vanstone) Reduction という。
- Tate pairing を用いるものを FR (Frey-Rück) Reduction という。
まとめ
楕円曲線暗号の雰囲気を味わうことができたと思います。
ここでは天下り的な感じでしたが、代数幾何が分かると楕円曲線と同型な幾何的な構造や特異点の分解などなど色々理解できて楽しいので是非勉強してみてください!
Discussion
大抵の場合かなり少ない数になるとは言えないです (b をどのように選んでもハッセの定理から群の位数はおよそ p 程度になるため)
言えるのは「小さい位数の点を含むようになる」などであり、攻撃者は点を自由に選べるので小さい位数の点を選びたい放題になります