数学オリンピック2018 1次予選解説 その3

はじめに

※本記事は、2018/2/8にHatenaBlogに投稿した記事を移行したものです
前回に引き続き、数学オリンピック国内1次予選 ( JMO ) の解説です。オリジナルの問題、解答 ( 答えの数値だけ ) は、こちらに公開されています。

• 問1～問6 … その1
• 問7～問9 … その2
• 問10,11 … 今回
• 問12 … その4

問題と解説

問題文の詳細については、冒頭のリンクよりご参照ください。以下では要約した問題文で説明していきます。

問10

問題・答え

8人の選手で総当たり戦を行った際の勝敗の状況として、次の条件を満たすのは何通りか。ただし引き分けはないものとする。

• その8人でトーナメントを行った場合、トーナメントの組み方により優勝者となる可能性のある人は2人である。ただし前提として、トーナメントの各試合の勝敗が総当たり戦の時と同じだとする。

※トーナメントの試合の進め方の詳細がオリジナルの問題に記されていますが、世間一般的なトーナメント方式 ( 誰でも3連勝で優勝 ) と考えて問題ないと思いますので、ここでは割愛します。

答え: 344064通り

解説

まあなんというか、丁寧に条件を解きほぐしていくよりなさそうです。

まずは「優勝者となる可能性のある人は2人」ということなので、その2人をA,Bと名付け、AがBに勝つものとします。
ここで明確にしておきたいのはこの「可能性」の意味です。これはつまり、次の2つのことを指しています。

• 総当たり戦の勝敗状況のままA,Bを優勝させるトーナメントの組み方がある。
• 総当たり戦の勝敗状況のままでは、A,B以外が優勝となるトーナメントの組み方はない。( 必ずA,Bどちらかが優勝する )

後者の方が意識から抜けがちなので注意したいところです。

では、Aの勝敗状況から行きます。もしAが全勝するとどうなるでしょうか? …それはもちろん、誰もAを負かせないので、常にAが優勝です。これはBの優勝の可能性が消えてしまいますからN.G.ということになります。つまりAに勝つ人が存在する ことを意味します。AはBに勝つという前提ですから、それはB以外の人になるはずです。
続いて、ではそのAに勝つ人は複数でしょうか? しかしもし複数いて、そのうち2人をC1,C2 ( C1はC2に勝つ ) とすると、次のトーナメントを組んだ時、A,Bとも優勝できません。

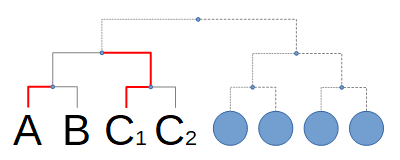
つまり、Aに勝つ人は1人だけです。それをCと名付けておきます。またこれで、Aの勝敗はC以外に全勝と確定しました。

次に、新しく出てきたCの勝敗状況を考えてみます。CはAに勝ちますが、それ以外の人に対してはどうでしょうか。
さきほどと似たトーナメントを組んでみると分かります。もしCがA,B以外の誰か ( Dとします ) に勝つようだと、A,Bとも優勝できずN.G.です。

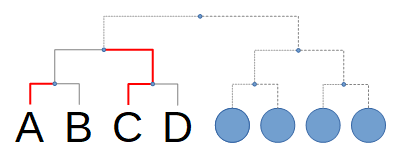
じゃあ、CがBに勝つのはどうかというと、今度は別のトーナメントでA,Bとも優勝できないパターンができます。

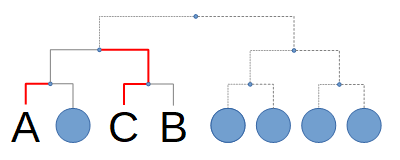
結局、CがA以外の誰かに勝つのはマズいということです。これで、Cの勝敗はA以外に全敗と確定しました。

残るは ( 多分 ) Bだけです。BはAに負けてCに勝ちます。ではそれ以外の人に対してはどうでしょうか。
ところが、もしBがA,C以外の誰か ( Dとします ) に負けるようだと、次のトーナメントでA,B仲良く1回戦敗退でN.G.です。

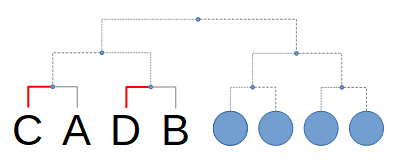
ということで、Bは他の人に負けるわけには行きません。これで、Bの勝敗はA以外に全勝と確定しました。

ここまで整理してみます。

• AはC以外に全勝
• BはA以外に全勝
• CはA以外に全敗

では、他の人の条件はどうでしょうか。他の人は、A,Bには負け、Cには勝つところまで確定しています。
しかし、実は他の人の勝敗がどうであれA,B,Cの条件だけで、AまたはBの優勝が確定しているのです。次のように場合分けして考えてみます。

• A,C が1回戦で当たるトーナメント
  • Aは1回戦敗退
  • Bは1回戦も含め、全試合Aと当たらないため全勝
  • つまりBが優勝
• A,C が1回戦で当たらないトーナメント
  • Cは1回戦敗退
  • Aは1回戦も含め、全試合Cと当たらないため全勝
  • つまりAが優勝

この通り、A,B,C以外の勝敗は優勝者に全く影響を与えません。ということで、これで十分、条件は全て出揃いました。

後は組み合わせの計算です。

• 8人中、A,B,Cの役回りが誰になるか ${}_8 P_{3}=336$通り
• 残り5人の勝敗、計${}_5 C_{2}=10$試合で、それぞれ勝ち負けどちらでも良いので、$2^{10}=1024$通り
• トータルで、$336\times 1024=344064$通り

ということで、344064通りが答えとなります。

問11

問題・答え

以下の条件を満たす正の整数$n$は幾つ存在するか。

• $n$を7進法表記した ( ただし最上位の桁は0ではない ) 場合の桁数$k$が2以上であり、
• 7進法表記した$n$から、それぞれ1桁目～$k -1$桁目を取り除いてできる$k -1$個の$k -1$桁7進法表記の数の総和が$n$に等しい。

答え: 42

解説

ちょっと問題が掴み辛いので、例を挙げてみます。

例えば、十進法での4649は、7進法では5桁の 16361 です。実際、 $4649=1\times 7^4+6\times 7^3+3\times 7^2+6\times 7^1+1\times 7^0$ が成立していますから。
ここから、1～4桁目を取り除いてできる数、1636, 1631, 1661, 1361 これを7進法表記として足し算すると、7進法10252、あるいは十進法で2536です。

ただ、この合計は元の数とは異なりますから、問題の条件は満たさないということになります。

…直感的には、桁を1つ抜いてできる数は、( 7進法での1桁の増減は7倍分に相当するので ) ほぼ元の 1/7 の大きさと見ると、7個分合計してやっと元の数と同等、つまり元の$n$の桁数$k$は8 ( $k -1=7$ ) なんじゃないかと思えます。とは言っても、その前後の桁数 ( 6桁や9桁 ) でも条件を満たす数がある可能性もありますし、まずは大きさを大まかに見積もって桁数を確定させることを考えます。

では見積もりですが、$n$の上位2桁だけだと流石に粗そうな気がするので、上位3桁を使ってやってみます。…というと$k =2$のケースが置き去りになってしまいますが、2桁の数では明らかに条件を満たせないので ( 桁を抜いた数1個だけでは元の数より明らかに小さい )、特に問題はありません。

では、$n$の7進法での上位3桁を$abc~(1\le a\le 6,~0\le b,c\le 6)$とします。そうすると、$n$自体の大きさは次のように見積もれます。

• $0\le \frac{n}{7^{k-3}}-(49a+7b+c)\lt 1$

次に、桁を抜いた数$k -1$個分の総和についてです。上から2番目の桁を抜いてできる数は7進法で$ac\cdots$ですが、それ以外の桁を抜いてできる$k -2$個は全て$ab\cdots$となります。そのため、この総和を$S$とすると、

• $0\le \frac{S}{7^{k-3}}-\{7(k-1)a+(k-2)b+c\}\lt k-1$

では、$n=S$の仮定のもと、両不等式を合成します。

$$0\le \frac{n}{7^{k-3}}-(49a+7b+c)\lt 1 \Leftrightarrow -1\lt(49a+7b+c)-\frac{n}{7^{k-3}}\le 0 \\ 0\le \frac{S}{7^{k-3}}-\{7(k-1)a+(k-2)b+c\}\lt k-1 と辺々足し合わせて \\ -1\lt (49a+7b+c)-\frac{n}{7^{k-3}}+\frac{S}{7^{k-3}}-\{7(k-1)a+(k-2)b+c\} \lt k-1 \\ \Rightarrow -1\lt (49a+7b+c)-\{7(k-1)a+(k-2)b+c\} \lt k-1~\because n=S \\ \Leftrightarrow -1\lt 7(8-k)a+(9-k)b \lt k-1 \\ \Leftrightarrow 0\lt (8-k)(7a+b)+b+1 \lt k \\$$

こうしてみると、$7a+b$の部分は7以上ですから、

• $k$が小さい場合: $k\le 7$であれば、不等式の中央部分が8以上なのに対し、右辺$k$が7以下で不適
• $k$が大きい場合: $k\ge 9$であれば、不等式の中央部分が0以下 ( $b$は6以下であることに注意 ) なので、左側の不等号が成立せず不適

これで、桁数$k=8$が必要であると分かりました。なので、実際に桁の数字の条件を調べてみます。

実際に桁を抜いた数を並べて、7進法のまま総和$S$を表現してみます。$n$を7進法で表記した場合の下位の桁から $d_1,d_2,\cdots d_8~( 0\le d_1,\cdots,d_7\le 6, 1\le d_8\le 6 )$ としています。そうすると、次の図のように$n$の桁と共通部分があることが分かります。

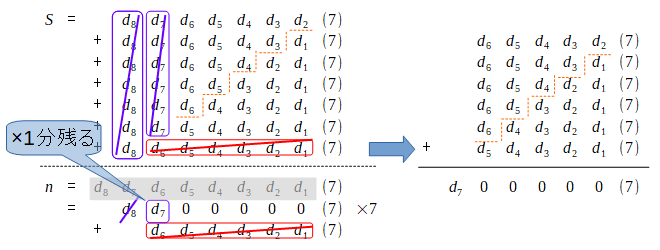
この時、ちょっと工夫として$n$の上位2桁を１つずらして ( 代わりに7倍するので大きさは同じ )、同じ桁同士で見比べられるようにしています。そうすると、共通部分を相殺することで、1種の7進法覆面算ができあがります。これを解いてあげれば良いということです。

そうして覆面算を解いていくわけですが…。この時、各桁で繰り上がりが発生し得ますから、それを次の図のように $c_2,c_3,\cdots,c_6$ とします。

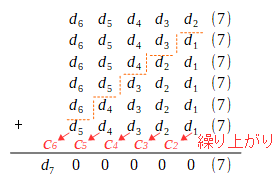
そうすると次の条件が分かります。

• $d_2+5d_1\equiv 0~mod~7,~c_2=(d_2+5d_1)/7~( 0\le c_2\le 5 )$
• $2d_3+4d_2+c_2\equiv 0~mod~7,~c_3=(2d_3+4d_2+c_2)/7~( 0\le c_3\le 5 )$
• $3d_4+3d_3+c_3\equiv 0~mod~7,~c_4=(3d_4+3d_3+c_3)/7~( 0\le c_4\le 5 )$
• $4d_5+2d_4+c_4\equiv 0~mod~7,~c_5=(4d_5+2d_4+c_4)/7~( 0\le c_5\le 5 )$
• $5d_6+d_5+c_5\equiv 0~mod~7,~c_6=(5d_6+d_5+c_5)/7~( 0\le c_6\le 5 )$
• $d_7=c_6$

mod 7 なのは7進法の筆算だから、なのと、繰り上がりが0～5の範囲に収まるのは6個の数の加算だからですね。…しかし、良く見ると結構規則正しい形をしています。そこで、次のようにまとめられそうです。

• $(i-1)d_i+(7-i)d_{i-1}+c_{i-1}\equiv 0~mod~7,~c_i=\{ (i-1)d_i+(7-i)d_{i-1}+c_{i-1} \}/7~( 2\le i\le 6 )$
• $d_7=c_6$

なお、便宜上繰り上がりの来ない1桁目用に$c_1=0$として文字を合わせています。

さてそうすると、7というのは素数ですから、一般に剰余方程式$ax\equiv 1~mod~7$というのは$a\not\equiv 0$の場合、必ず解が1つに決まります ( なおこの解のことを$a^{-1}$と書いたりします。例えば$2\times 4\equiv 1\Leftrightarrow 2^{-1}\equiv 4$ )。ということは、この条件、$d_1$を決めればそのまま将棋倒し的に$d_7$まで一意に決まる ( かつ必ず解がある ) と言えます。具体的には次の通りです。なお、計算上の便宜として$e_i=d_i-c_i~( e_1=d_1 )$を導入しています。

$$\begin{aligned} &~(i-1)d_i+(7-i)d_{i-1}+c_{i-1}\equiv 0~mod~7 \\ \Leftrightarrow&~(i-1)d_i\equiv(i-7)d_{i-1}+e_{i-1}-d_{i-1}~mod~7 \\ \Leftrightarrow&~(i-1)d_i\equiv(i-1)d_{i-1}+e_{i-1}~mod~7 \\ \Leftrightarrow&~d_i\equiv d_{i-1}+(i-1)^{-1}\cdot e_{i-1}~mod~7 \\ \\ &~c_i=\{ (i-1)d_i+(7-i)d_{i-1}+c_{i-1} \}/7 \\ \Leftrightarrow&~d_i-e_i=\{ (i-1)d_i+(7-i)d_{i-1}+d_{i-1}-e_{i-1} \}/7 \\ \Leftrightarrow&~e_i=\{ (8-i)(d_i-d_{i-1})+e_{i-1} \}/7 \\ \\ &~d_7=d_6-e_6 \end{aligned}$$

ということで、$d_1=0,1,\cdots,6$の7通りそれぞれに対して$d_2,d_3,\cdots,d_7$が1通りずつ決まると分かりました。問題としては個数を求めれば良いので、各$d_i$の値を求める必要はないのですが、実際に計算してみると次のようになります。

• $d_1=0 ( e_1=0 )$の場合
  trivialに $d_2=d_3=d_4=d_5=d_6=d_7=0$
• $d_1=1 ( e_1=1 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=2, e_2=\{6\times(d_2-d_1)+e_1\}/7=1$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=6, e_3=\{5\times(d_3-d_2)+e_2\}/7=3$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=0, e_4=\{4\times(d_4-d_3)+e_3\}/7=-3$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=1, e_5=\{3\times(d_5-d_4)+e_4\}/7=0$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=1, e_6=\{2\times(d_6-d_5)+e_5\}/7=0$
  • $d_7=d_6-e_6=1$
• $d_1=2 ( e_1=2 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=4, e_2=\{6\times(d_2-d_1)+e_1\}/7=2$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=5, e_3=\{5\times(d_3-d_2)+e_2\}/7=1$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=3, e_4=\{4\times(d_4-d_3)+e_3\}/7=-1$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=1, e_5=\{3\times(d_5-d_4)+e_4\}/7=-1$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=5, e_6=\{2\times(d_6-d_5)+e_5\}/7=1$
  • $d_7=d_6-e_6=4$
• $d_1=3 ( e_1=3 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=6, e_2=\{6\times(d_2-d_1)+e_1\}/7=3$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=4, e_3=\{5\times(d_3-d_2)+e_2\}/7=-1$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=6, e_4=\{4\times(d_4-d_3)+e_3\}/7=1$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=1, e_5=\{3\times(d_5-d_4)+e_4\}/7=-2$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=2, e_6=\{2\times(d_6-d_5)+e_5\}/7=0$
  • $d_7=d_6-e_6=2$
• $d_1=4 ( e_1=4 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=1, e_2=\{6\times(d_2-d_1)+e_1\}/7=-2$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=0, e_3=\{5\times(d_3-d_2)+e_2\}/7=-1$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=2, e_4=\{4\times(d_4-d_3)+e_3\}/7=1$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=4, e_5=\{3\times(d_5-d_4)+e_4\}/7=1$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=0, e_6=\{2\times(d_6-d_5)+e_5\}/7=-1$
  • $d_7=d_6-e_6=1$
• $d_1=5 ( e_1=5 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=3, e_2=\{6\times(d_2-d_1)+e_1\}/7=-1$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=6, e_3=\{5\times(d_3-d_2)+e_2\}/7=2$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=2, e_4=\{4\times(d_4-d_3)+e_3\}/7=-2$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=5, e_5=\{3\times(d_5-d_4)+e_4\}/7=1$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=1, e_6=\{2\times(d_6-d_5)+e_5\}/7=-1$
  • $d_7=d_6-e_6=2$
• $d_1=6 ( e_1=6 )$の場合
  • $d_2\equiv d_1+1^{-1}\cdot e_1\Rightarrow d_2=5, e_2=\{6\times(d_2-d_1)+e_1\}/7=0$
  • $d_3\equiv d_2+2^{-1}\cdot e_2\Rightarrow d_3=5, e_3=\{5\times(d_3-d_2)+e_2\}/7=0$
  • $d_4\equiv d_3+3^{-1}\cdot e_3\Rightarrow d_4=5, e_4=\{4\times(d_4-d_3)+e_3\}/7=0$
  • $d_5\equiv d_4+4^{-1}\cdot e_4\Rightarrow d_5=5, e_5=\{3\times(d_5-d_4)+e_4\}/7=0$
  • $d_6\equiv d_5+5^{-1}\cdot e_5\Rightarrow d_6=5, e_6=\{2\times(d_6-d_5)+e_5\}/7=0$
  • $d_7=d_6-e_6=5$

ということで、全部で7通り…あれ? 何か忘れてるような。そうです、条件を整理している中で消えてしまった$d_8$がありました。これは消えてしまったということはどんな値を設定しても良いということを意味しますので、1～6の6通りがそれぞれの組に対して設定できるわけです。

ということで、これが本当に最後です。$7\times 6=42$で42個が答えとなります。

終わりに

いよいよ次で最後です。やはり最後までまとめて書くのはきつかった。