数学オリンピック2018 1次予選解説 その2

はじめに

※本記事は、2018/2/7にHatenaBlogに投稿した記事を移行したものです
前回に引き続き、数学オリンピック国内1次予選 ( JMO ) の解説です。オリジナルの問題、解答 ( 答えの数値だけ ) は、こちらに公開されています。

• 問1～問6 … その1
• 問7～問9 … 今回
• 問10,11 … その3
• 問12 … その4

問題と解説

問題文の詳細については、冒頭のリンクよりご参照ください。以下では要約した問題文で説明していきます。

問7

問題・答え

1～12の12個の数を2個ずつ6組のペアに分ける方法の中で、次の条件を満たすのは何通りか。

• 条件: 各ペア$(i,j)$における$|i-j|$ ( 2数の差の絶対値 ) の合計が30に等しい

答え: 1104通り

解説

ペアに分けて差の絶対値を合計…? と悩んでも前に進まないので、合計が30かどうかはともかくペアを作って試してみます。

例えば、(1,2),(3,4),(5,6),(7,8),(9,10),(11,12) と分けたとしましょう。その時の差の絶対値の合計は次のようになります。

$$\begin{aligned} &~(2-1)+(4-3)+(6-5)+(8-7)+(10-9)+(12-11) \\ &=(2+4+6+8+10+12)-(1+3+5+7+9+11) \\ &=6 \end{aligned}$$

結果の6というのはこの際重要ではなく、プラスに働く6数とマイナスに働く6数を分離しているということが重要です。更にもう一歩進めると、

$$\begin{aligned} &~(2-1)+(4-3)+(6-5)+(8-7)+(10-9)+(12-11) \\ &=(2+4+6+8+10+12)-(1+3+5+7+9+11) \\ &=(1+2+3+4+5+6+7+8+9+10+11+12)-2\times(1+3+5+7+9+11) \\ &=78-2\times(1+3+5+7+9+11) \\ &=6 \end{aligned}$$

つまりどういうことかと言うと、マイナスに働く数のみで結果が分かってしまうので、マイナス側のみ意識すれば良いということです。
今回、式の値が30ですから、$78-2\times 24=30$ ということで、マイナス側の6数の合計が24であることが分かります。

では、実際にそのような6数の組み合わせを調べてみましょう。…実は意識しなくても結果に影響はないのですが、「2数のペア」とした時に 1 は必ずマイナス側に来ること、12は必ずプラス側に来ることから、もう少し正確には、2～11の中で合計が23となる5数と1がマイナス側の数ということになります。

で、列挙してみると、(1,2,3,4,5,9), (1,2,3,4,6,8), (1,2,3,5,6,7) の3通りの組み合わせです。そうするとプラス側は逆の6数、順に(6,7,8,10,11,12), (5,7,9,10,11,12), (4,8,9,10,11,12) なのですが、そこからペアの組み方を考える必要があります。この時に、マイナス側の数よりプラス側の数の方が大きくなるように注意が必要です。

では、それぞれの組み合わせで数え上げてみます。

• マイナス側(1,2,3,4,5,9)、プラス側(6,7,8,10,11,12)
  • 9とペアにできるのは10,11,12の3通り。
  • それ以外は任意に組んでも大小関係は問題にならない。
  • ということで、このケースは $3\times 5!=360$通り
• マイナス側(1,2,3,4,6,8)、プラス側(5,7,9,10,11,12)
  • 8とペアにできるのは9,10,11,12の4通り。
  • 5とペアにできるのは1,2,3,4の4通り。
  • それ以外は任意に組んでも大小関係は問題にならない。
  • ということで、このケースは $4\times 4\times 4!=384$通り
• マイナス側(1,2,3,5,6,7)、プラス側(4,8,9,10,11,12)
  • 4とペアにできるのは1,2,3の3通り。
  • それ以外は任意に組んでも大小関係は問題にならない。
  • ということで、このケースは $3\times 5!=360$通り

出てきた場合の数を合計して 1104通り、これが答えになります。

問8

問題・答え

$a_1,a_2,\cdots,a_6$および$b_1,b_2,\cdots,b_6$、$c_1,c_2,\cdots,c_6$の3組は、それぞれ1～6の並び替えである。この時、次の計算式の取り得る最小値を求めよ。

• $a_1 b_1+a_2 b_2+\cdots a_6 b_6+b_1 c_1+b_2 c_2+\cdots b_6 c_6+c_1 a_1+c_2 a_2+\cdots c_6 a_6$

答え: 195

解説

対称性のある綺麗な形ではあるのですが、積の形のまま値の大小を見積もるのは苦しいところがあります。せめて和の形であれば…。

とすると、次のような対称式の変形が使えないでしょうか?

$$(a+b)^2=(a^2+b^2)+2ab \\ \therefore ab=\frac{1}{2}\{ (a+b)^2-(a^2+b^2) \}$$

もう一声。この問題では$a,b$の他に$c$も現れますので、$s=a+b+c$ とおいてみましょう。そうすると、

$$ab=\frac{1}{2}\{ (a+b)^2-(a^2+b^2) \}=\frac{1}{2}\{ (s-c)^2-(a^2+b^2) \} \\ bc=\frac{1}{2}\{ (s-a)^2-(b^2+c^2) \} \\ ca=\frac{1}{2}\{ (s-b)^2-(c^2+a^2) \}$$

$$\begin{aligned} \therefore ab+bc+ca&=\frac{1}{2}\{ (s-a)^2+(s-b)^2+(s-c)^2-(a^2+b^2)-(b^2+c^2)-(c^2+a^2) \} \\ &=\frac{1}{2}\{ 3s^2-2(a+b+c)s-(a^2+b^2+c^2) \} \\ &=\frac{1}{2}( s^2-a^2-b^2-c^2 ) \end{aligned}$$

と平方の和・差だけという綺麗な形になりました。

トリッキーな変形だと思われるでしょうか? しかし、統計での分散/標準偏差の計算をやったことがあれば、似たような変形があるのでは…? ともあれ、本命の式に移りましょう。これを$S$としておきます。

$$\begin{aligned} S&=a_1 b_1+a_2 b_2+\cdots a_6 b_6+b_1 c_1+b_2 c_2+\cdots b_6 c_6+c_1 a_1+c_2 a_2+\cdots c_6 a_6 \\ &=\sum_{i=1}^{6} (a_i b_i+b_i c_i+c_i a_i) \\ &=\sum_{i=1}^{6} \frac{1}{2}( s_i^2-a_i^2-b_i^2-c_i^2) \\ &=\frac{1}{2}( \sum_{i=1}^{6} s_i^2-\sum_{i=1}^{6} a_i^2-\sum_{i=1}^{6} b_i^2-\sum_{i=1}^{6} c_i^2 ) \end{aligned}$$

なお、途中から出てくる$s_i$は$s_i=a_i+b_i+c_i$ だと考えて下さい。

さて、$a_1,\cdots,a_6$等はそれぞれ1～6の並べ替えですから、最後の形に出てくる$\sum_{i=1}^{6} a_i^2,~ ~\sum_{i=1}^{6} b_i^2,~ ~\sum_{i=1}^{6} c_i^2$、これらは全て$1^2+2^2+\cdots+6^2=91$と不変になります。ということは、考えるべきは$\sum_{i=1}^{6} s_i^2$のみで済むということです。

$s_i$については、$a_i, b_i, c_i$の値がどう組み合わせられるかで変わります。しかしながら、次の計算から分かるようにその合計は不変です。

$$\begin{aligned} \sum_{i=1}^6 s_i&=\sum_{i=1}^6 (a_i+b_i+c_i) \\ &=\sum_{i=1}^6 a_i+\sum_{i=1}^6 b_i+\sum_{i=1}^6 c_i \\ &=(1+2+\cdots+6)+(1+2+\cdots+6)+(1+2+\cdots+6) \\ &=63 \end{aligned}$$

つまり、この問題は最終的に「和が一定(63)の$s_i$の平方和の最小値を求めよ」というところに帰着されそうです。

こういう場合、各$s_i$をなるべく同じ値に揃えてあげることで平方和を小さくすることができます。
※詳細は省きますが、統計の話で、平均(合計)一定の状況で分散と2乗平均(平方和÷要素数)の大小が連動することを考えると良いのではないでしょうか。

とは言え63は6で割り切れませんから、なるべく同じ値だと、10,10,10,11,11,11 です。この時$\sum_{i=1}^{6} s_i^2=663$、最終的な答えは、次のようになります。

$$S_{min}=\frac{1}{2}( \sum_{i=1}^{6} s_i^2-\sum_{i=1}^{6} a_i^2-\sum_{i=1}^{6} b_i^2-\sum_{i=1}^{6} c_i^2 )=\frac{1}{2}(663-91\times 3)=195$$

めでたしめでたし。と言いたい所ですが、ウラは取らねばなりません。本当に$s_i$が10,10,10,11,11,11の組み合わせになるような$a_i, b_i, c_i$が構成できるのか? というところ。

ただこれは、例えば $10=1+3+6,~11=2+4+5$あたりからサイクリックに値を割り振ることで容易にできます。この例で言うと次とか。

$$\begin{aligned} a_1&=1, a_2&=3, a_3&=6,~ ~a_4&=2, a_5&=4, a_6&=5 \\ b_1&=3, b_2&=6, b_3&=1,~ ~b_4&=4, b_5&=5, b_6&=2 \\ c_1&=6, c_2&=1, c_3&=3,~ ~c_4&=5, c_5&=2, c_6&=4 \\ \end{aligned}$$

ということでウラも取れたのでこれで本当に決着です。

問9

問題・答え

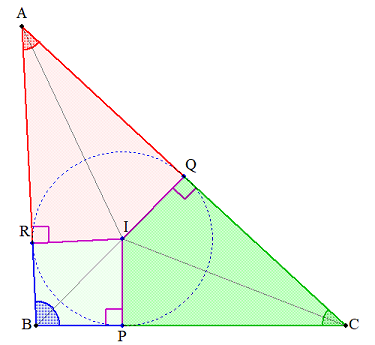
次の図の中で、DEの長さを求めよ。

なお、点Iは△ABCの内接円の中心、点Jは傍接円の中心、点P,Q,Rは内接円と各辺の、点S,T,Uは傍接円と各辺の接点です。
※点Jは問題文に現れていませんが、不便なので名前を付けました。
※図中、鋭角に見えるから鋭角、鈍角に見えるから鈍角だとは限りません。なお、P,Sの位置関係は左右逆の可能性もありますが…。逆になっても状況は同じなので、この図では決め打って描いています。

答え: $\frac{4\sqrt{2}}{3}$

解説

図がごちゃごちゃしていて訳が分かりません。なので、取り敢えず内接円/内心・傍接円/傍心に関わる性質を整理していきましょう。

内接円/内心と傍接円/傍心の性質

まずは内接円とその中心、内心。三角形の内角の二等分線の交点なのですが、その理解ではややぬるい。
次の図のように、内心を中心にして三角形が3組の合同な直角三角形に分割される、まで踏み込みたいところです。つまり、同じ長さの線分や同じ大きさの角のペア、直角が色々できるわけです。

続いて傍接円とその中心、傍心。三角形のある内角と他の2つの外角の二等分線の交点です。今回の問題では内角としてAを選択。これも内心同様、3組の合同な直角三角形が現れます。

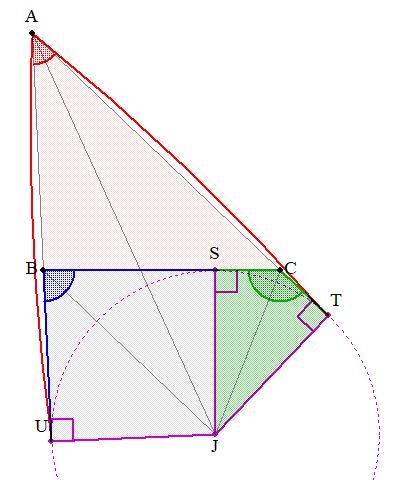
…と。ここまでなら、それほどインパクトもありません。しかしこの2つを組み合わせると凄いことになります。

お判りでしょうか? 内心の時に出てきた線分の長さ・角の大きさが、傍心側の話にも侵食し、至る所で同じ長さ・角度、垂直の関係が発生するのです。実にこれだけあります。

• 同じ長さ
  • 内接円の半径 IP=IQ=IR (紫)
  • 傍接円の半径 JS=JT=JU (薄紫)
  • AQ=AR (赤)
  • BP=BR=CS=CT (青)
  • CP=CQ=BS=BU (緑)
  • BC=QT=RU (青+緑)
• 同じ角度
  • ∠IAQ=∠IAR (赤)
  • ∠IBP=∠IBR=∠BJS=∠BJU=∠IJC (青)
  • ∠ICP=∠ICQ=∠CJS=∠CJT=∠IJB (緑)
• 垂直
  • IP⊥BC, IQ⊥CA, IR⊥AB (内接円の半径と接線)
  • JS⊥BC, JT⊥CA, JU⊥AB (傍接円の半径と接線)
  • IB⊥JB, IC⊥JC

なお、A,I,Jは同一直線上です。

本題

というところで、再度問題を見直します。そのままだと情報過多なので、ちょっと ( 大分 ) 間引きました。
※なお、D,Eは実は線分IJ上に来るのですが、そのことは考えなくても解くのに支障はありません。

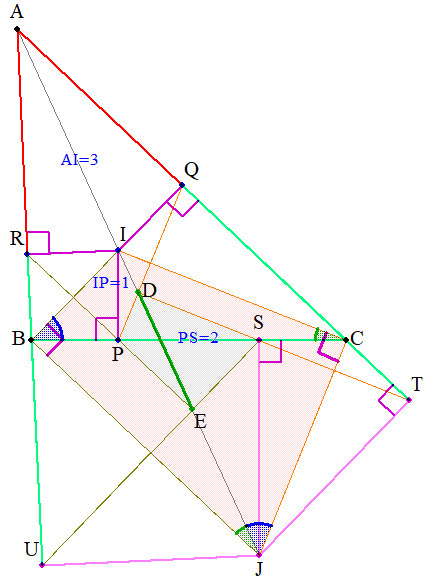
…すると、実は□PDSEと□IBJCは相似です。そのため、$PS:DE=IJ:BC$

一方で、△AJTに着目すると、IQ,JTは平行 ( なぜならば共にATに垂直 ) ですから、$IJ:QT=AI:AQ$

で、上で整理したことから $BC=QT$

まとめると、

$$\begin{aligned} PS:DE&=IJ:BC \\ &=IJ:QT \\ &=AI:AQ \\ \therefore DE&=\frac{AQ\times PS}{AI} \end{aligned}$$

分かってないのは、そうするとAQのみですが、これは$AQ=\sqrt{AI^2-IQ^2}=\sqrt{AI^2-IP^2}=2\sqrt{2}$と計算できます。
よって、$DE=\frac{4\sqrt{2}}{3}$ と言うことです。

いや、なぜ2つの四角形の相似なんて分かるのよ? というところですが、これは次の図のように整理することで導くことができます。

内心・傍心が絡むことで、合同な直角三角形を2つ合わせたパーツが至る所にありますから、そこから、色々垂直な関係が分かります。そこから、更に平行や垂直の関係も分かるのです。

• IC⊥PQ, JC⊥DT … もともと IC⊥JC なので、IC,DTは平行、PD⊥SD
  ⇒ 更に ∠DSPは同位角の関係にある∠ICPに等しい ( 緑 )
• IB⊥PR, JB⊥SU … もともと IB⊥JB なので、IB,SUは平行、PE⊥SE
  ⇒ 更に ∠ESPは錯角の関係にある∠IBPに等しい ( 青 )

ということで、2組の直角三角形の相似 △PDS∽△IBJ, △PES∽△ICJ が分かり、合わせて □PDSE∽□IBJC まで分かる、ということです。

終わりに

流石に後半に入ると難易度が上がってきます。図形の問題である問9、情報を整理するのは大変ですが ( 解説の図を描くのも大変でした )、相似の関係が綺麗に分かり、簡単な計算で解けるという面白い問題でした。

この後は一気に書き上げられると良いのですが…、まあ、ゆるゆる書き進めていきたいと思います。