ベイズ信頼区間からP値の類似物を作る（2項分布の例）

前置き

数理統計学の教科書にはよく「信頼区間は検定方式の反転によって得られる」ということが書かれている．少なくとも下記にリストした文献には記載がある．

• 『現代数理統計学の基礎』（久保川達也，共立出版；8章2節）
• 『新装改訂版　現代数理統計学』（竹村彰通，学術図書出版社；9章2節）
• 『数理統計学　データ解析の方法』（竹内啓，東洋経済新報社；7章Ⅲ）

すなわち仮説検定を棄却しない帰無仮説の範囲と信頼区間は同じである．

これの証明はほぼ「定義からただちに従う」みたいな感じだが，その意味は具体例を複数やらないとわかりにくいのではないか．そう思ってこれまでにいくつか記事を書いた（先に読んでおく必要はない）．

• 尤度比検定, ワルド検定, スコア検定から定まる信頼区間：二項分布の例
• ウィルコクソン検定から得られる信頼区間

今回はこれらと逆に，ベイズ信頼区間（Bayesian confidence interval; おなじものを信用区間 credible interval と呼ぶことも多い）から検定，P値を作る．すなわち，ベイズ信頼区間に含まれないパラメータの範囲を「棄却」する．

2項分布の例

取りうる値の上限 $n$ が決まっているカウントデータ（0以上の整数のデータ） $x$ に対して，モデルを2項分布，事前分布をベータ分布とする．すなわち，次のような生成モデルを考える．

$$\begin{aligned} x \mid p & \sim \mathrm{Binomial}(n,p)\\ p & \sim \mathrm{Beta}(a,b) \end{aligned}$$

このとき，2項分布のパラメータ $p$ の事後分布 $\pi(p|x)$ は次のベータ分布である．

$$\pi(p|x) = \mathrm{Beta}(x+a,\ n-x+b)$$

このことの説明は省略する．（ググれば解説が見つかると思うが私の好みに基づき）例えば ベイズ推論による機械学習入門（須山敦志，講談社） を参照してほしい．

R 言語で事後分布の95％区間を取るには次のようにする．

cibeta <- function(p, x, n, a=0.5, b=0.5, level=0.95){
  alpha = 0.5*(1-level)
  ahat <- x + a
  bhat <- n - x + b
  ql = qbeta(alpha, ahat, bhat, lower.tail=TRUE)
  qu = qbeta(alpha, ahat, bhat, lower.tail=FALSE)
  c(ql, qu)
}

これがベイズ信頼区間である．$a=0.5$, $b=0.5$ はよく使われる事前分布の一つであるジェフリーズ事前分布（Jeffreys prior）に相当する．

逆に，与えられたパラメータ $p$ を $(1-\alpha) 100$ ％信頼区間に含まない最小の $\alpha$ を取るには，次のようにする．

probbeta <- function(p, x, n, a=0.5, b=0.5){
  ahat <- x + a
  bhat <- n - x + b
  pl <- pbeta(p, ahat, bhat, lower.tail=TRUE)
  pu <- pbeta(p, ahat, bhat, lower.tail=FALSE)
  2*pmin(pl,pu)
}

これが欲しかったP値の類似物である．次のように信頼区間とともにプロットすると両者が整合することがわかる．

library(ggplot2)
z = seq(0.001, 0.999, length.out=301)

pv_beta <- probbeta(z,6,10)
CI <- cibeta(z,6,10)
df_beta <- data.frame(p=z, pv=pv_beta)

p1 = ggplot(data = df_beta, 
       aes(x=p, y=pv))+
  geom_line()+
  geom_errorbarh(data = NULL, aes(xmin = CI[1], xmax = CI[2], y=0.05), height=0.03, colour="cornflowerblue")+
  labs(y = "p-value")+
  theme_bw(16)

print(p1)

ここでは $x=6$, $n=10$ とした．

ジェフリーズ事前分布のほかに平坦事前分布（flat prior） $a=1$, $b=1$ もよく使われる．これらと，

• 尤度比検定, ワルド検定, スコア検定から定まる信頼区間：二項分布の例
• R の exact test についてのノート

に示した尤度比検定（LR）, ワルド検定（Wald）, スコア検定（score）と2項検定（exact）も合わせていくつかプロットしてみよう．$x$ を 1 から $n-1$ まで動かしている．

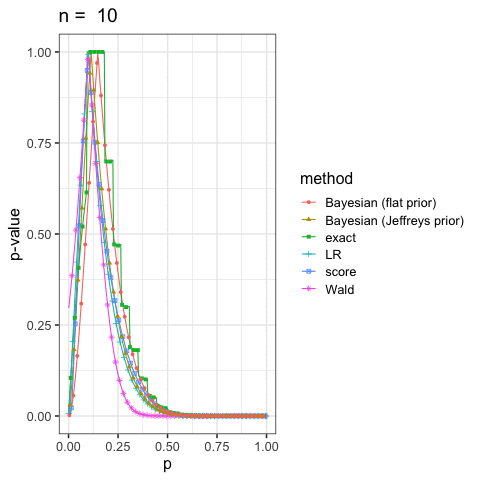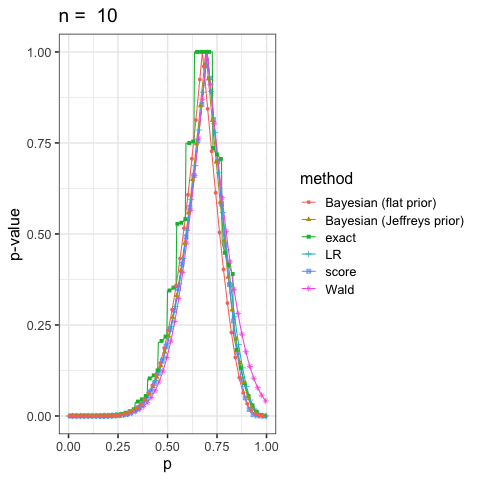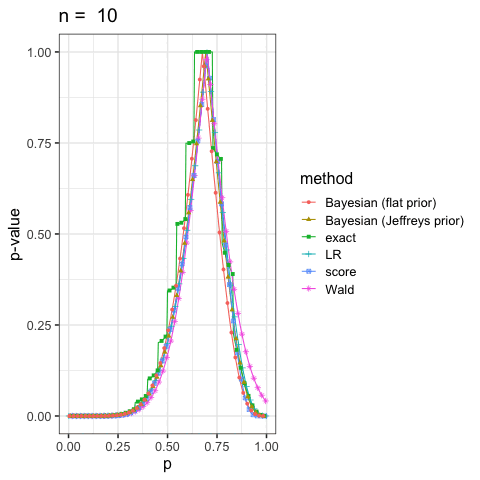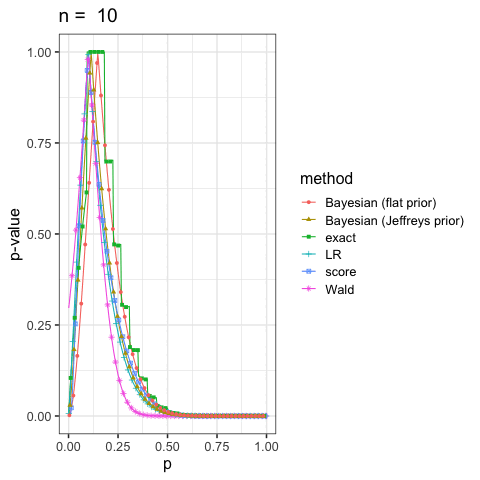
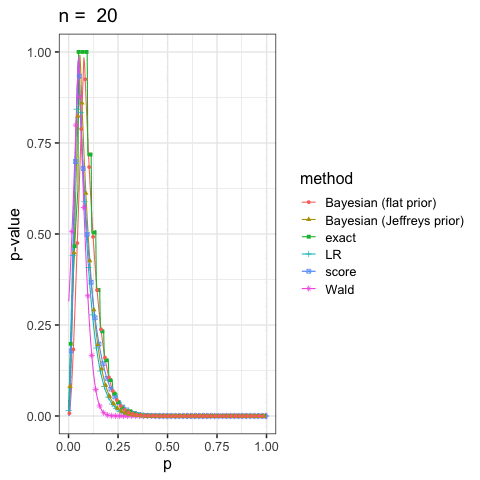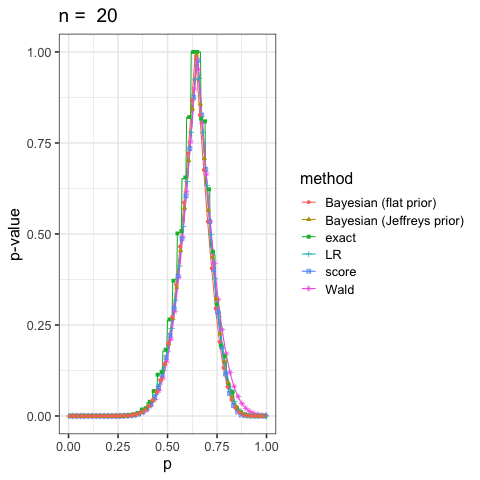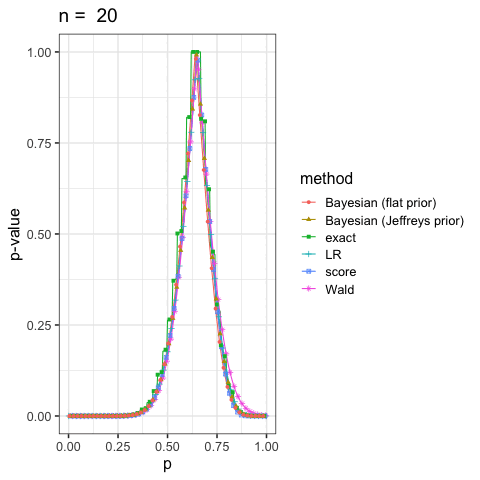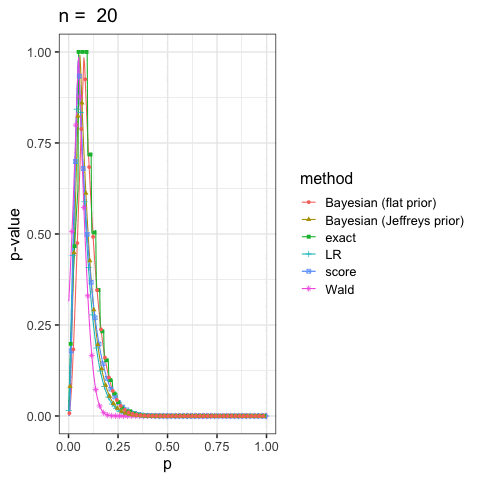
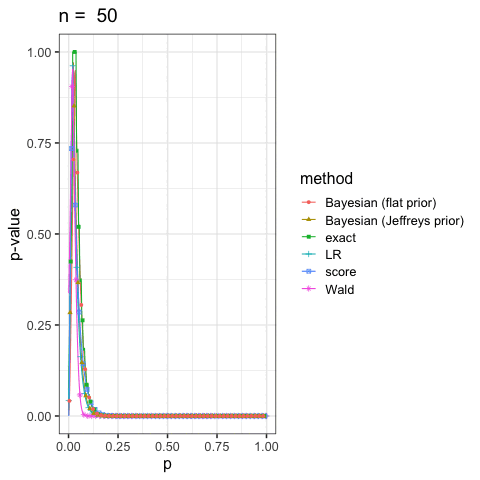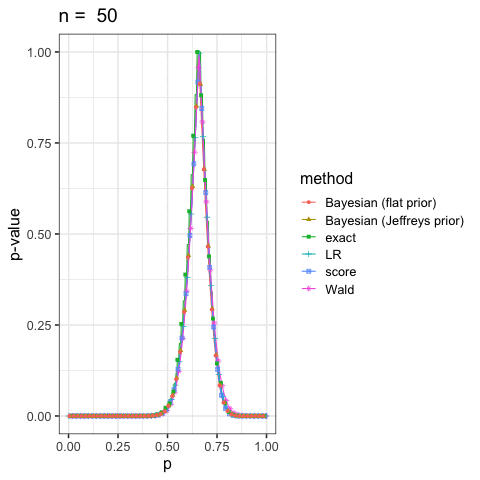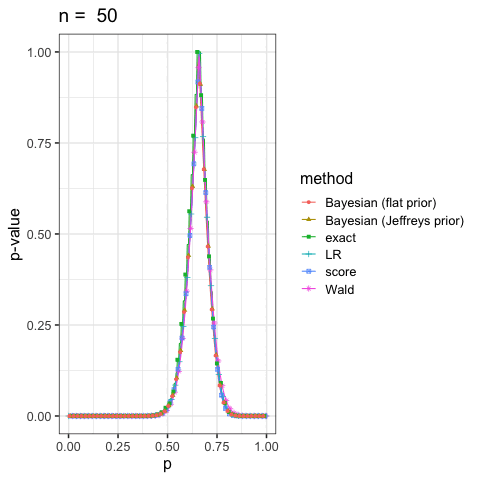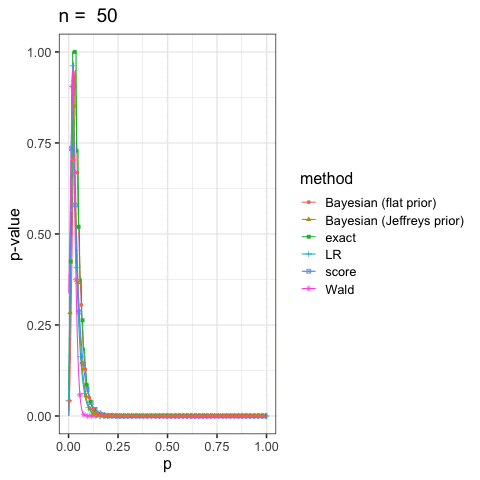
このように出発点の考え方が違っても $n$ が大きいときは似た結果が得られるというのは数理的なことを学ぶ上でおもしろい点の一つだと思う．

コードの全体はこちら：

https://github.com/abikoushi/Zenn_content/blob/main/R/bayesianpv_binom.R

やり残したこと・今後やりたいこと

• 最高事後密度区間（highest posterior densisty interval）版の信頼区間
• ベイズファクターと仮説検定の関係
• 統計的決定理論と仮説検定の関係