😊
R の exact test についてのノート

2024/08/26に公開
信頼区間
仮説検定
tech
 要約100(1-\alpha)% 信頼区間が \theta_0 を含まないことと有意水準 \alpha の仮説検定で帰無仮説 \theta_0 が棄却されることは同じのはずだが, R にデフォルトで入っている stats パッケージの exact test を行う関数（binom.test, poisson.test, fisher.test）を使うとこれが一致しないことがある.
これらの関数の p.value は定義通りに計算した p 値を返すが, conf.int は片側検定から定まる p 値の小さい方の2倍で計算した p 値と整合するように書かれているためと思われる.

 長い前置き: p 値について（再）入門するための手短な例統計的有意性と P 値に関する ASA 声明　(PDF 直リンク) には,「おおざっぱにいうと、P 値とは特定の統計モデルのもとで、データの統計的要約（たとえば、2 グループ比較での標本平均の差）が観察された値と等しいか、それよりも極端な値をとる確率である。」と記されている.
数式を使ってこの文を書き下してみよう.
統計モデルのパラメータ を\theta_0 とし, データの統計的要約, すなわちデータ X の関数である 検定統計量 を T(X) とする. 検定統計量 T(X) が観測された値 t の出る確率かそれより小さい確率になる確率の総和

p\text{-value} = \sum_t P_{\theta_0}(T(X) \le t) \tag{1}
が p 値である.
パラメータ\theta_0 を（例えば中央値=0のような形で）1つ決めたとしてもどんな確率分布で確率を測るかは決まらないので「特定の統計モデルのもとで」という断り書きが必要になる(パラメータ付きの確率分布で考えておくと, 例えば分布の仮定から多少外れていたときにp値がどうなるかといったロバストネスの議論などがしやすくなる).
通例は,
連続型の確率分布も含めるために和ではなく積分を使い,
帰無仮説が複数の点からなる場合も含めるために上界を使って
定義するので(1)式は統一的な定義ではない.
しかし第一歩として, (1)式を理解するための例をやってみる.
いま, 0または1の2値で表される変数　X=(X_1, \ldots, X_n) に対して, n=10 の観測のうち8回が1だった

T(X) = \sum_{i=1}^{n} X_i = 8
としよう.
「2値で表される変数」については病気のあり・なしとか, 成果のあり・なしといったイメージしやすいものをイメージして補ってほしい.
公平なコイントスのモデル, 確率パラメータ0.5の二項分布を使って p 値を計算してみる.
R のコード：

pb <- dbinom(0:10, 10, 0.5)

t_p <- dbinom(8, 10, 0.5)

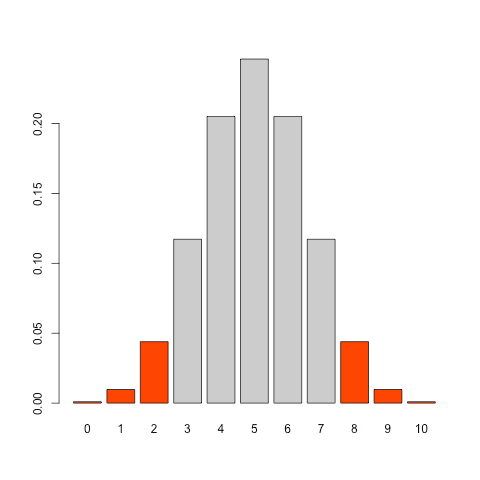
cols = ifelse(pb <= t_p, "orangered", "grey80")
png("binom_barplot.png")
barplot(pb, names.arg = 0:10, col=cols)
dev.off()


cat("p-value (by definition): ", sum(pb[pb <= t_p]), "\n")
実行結果:
> cat("p-value (by definition): ", sum(pb[pb <= t_p]), "\n")
p-value (by definition):  0.02148438 
棒グラフの赤いところをすべて足し合わせている（検定統計量 T(X) が観測された値 8 の出る確率かそれより小さい確率になる確率の総和）.
この計算は R では binom.test という関数で実装されている：
res0_b <- binom.test(x = 8, n = 10, p = 0.5)
cat("p-value (binom.test): ", res0_b$p.value, "\n")
print(res0_b$p.value)
実行してみると同じ結果が得られると思う.
ここで再度 統計的有意性と P 値に関する ASA 声明　(PDF 直リンク) にあたって,「P 値はデータと特定の統計モデル（訳注:仮説も統計モデルの要素のひとつ）が矛盾する程度をしめす指標のひとつである。」という一文に着目してみよう.
p値が小さいほど「矛盾の程度が大きい」のだから帰無仮説を動かしてp値を計算したら「矛盾の程度がそれなりに小さい仮説」や「矛盾の程度がそこそこの仮説」も知れるだろうというモチベーションが生まれる.
今回パラメータの取りうる値の範囲が0から1までなので総当たりでもさほど大変ではない.
library(ggplot2)
library(rootSolve)
library(MCMCpack)
z <- seq(0.1, 0.99, by=0.005)
pv_b <- sapply(z, function(p)binom.test(8, 10, p = p)$p.value)

ggplot(data = NULL)+
  geom_line(aes(x=z, y=pv_b))+
  geom_errorbarh(aes(y=0.05/2, xmin = res0_b$conf.int[1], xmax=res0_b$conf.int[2]),
                 height=0.03, colour="cornflowerblue")+
  theme_bw(16)+
  labs(x="param.", y="p-value", colour="method", linetype="method")
#ggsave("pvfun_b.png")
p 値が0.05になる高さでグラフを切ってやると95%信頼区間と一致……しない.
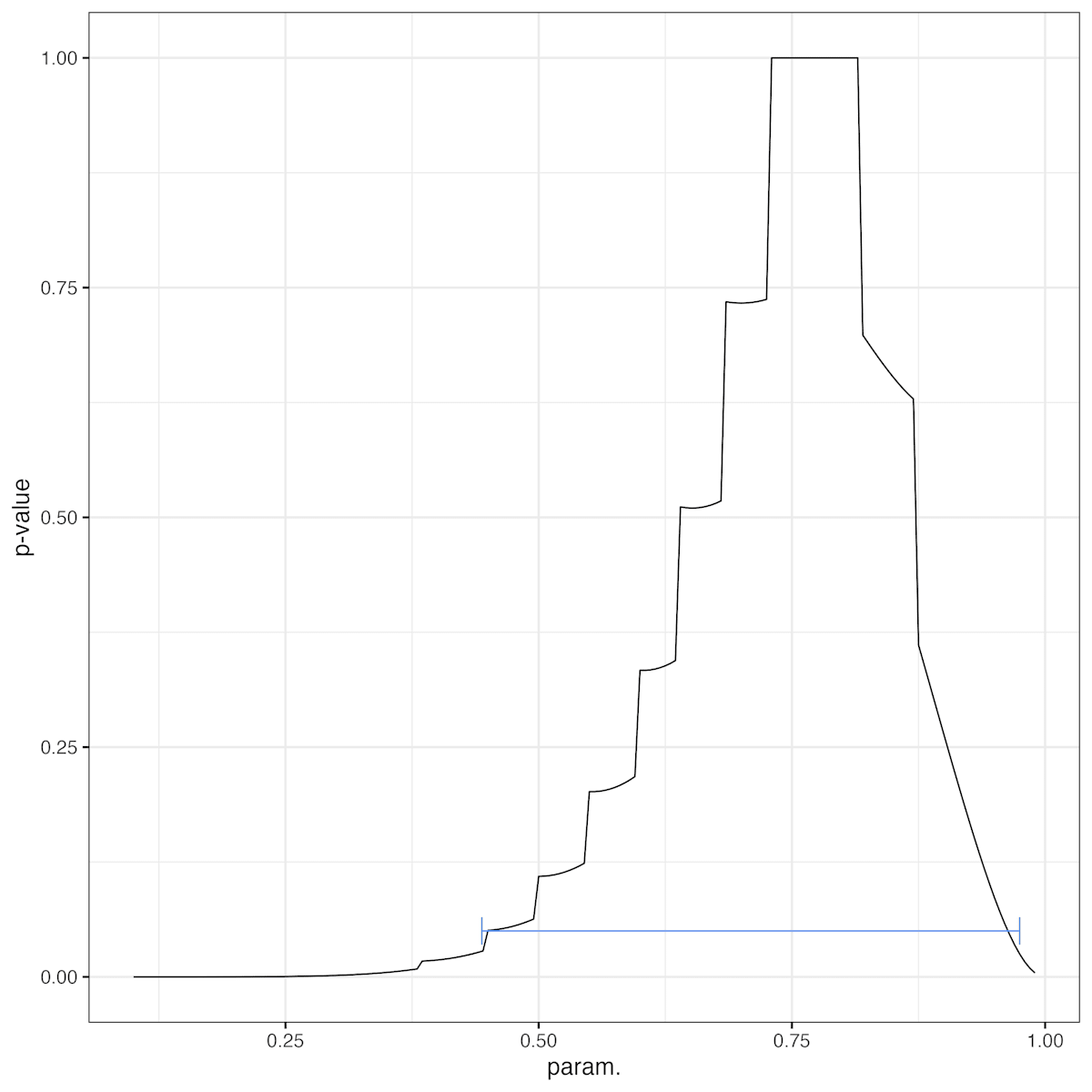
なぜか微妙に一致しない. 他の検定ではこれでうまくいっていたのに……. 参考：
尤度比検定, ワルド検定, スコア検定
ウィルコクソン検定
最初, この投稿は統計的有意性と P 値に関する ASA 声明　(PDF 直リンク) の補助テキストのような感じにできたらいいなと思って書き始めた.
しかしこのような不整合があるので路線を変更して先に "R の exact test についてのノート" を書くことにした（長い前置き終わり）.

 二項検定binom.test で信頼区間に p 値との不整合が生じた理由は, どうも異なる定義の方法を使っているかららしい.
つぎのように片側検定の p 値の2倍で両側検定の p 値を定義すると一致した.
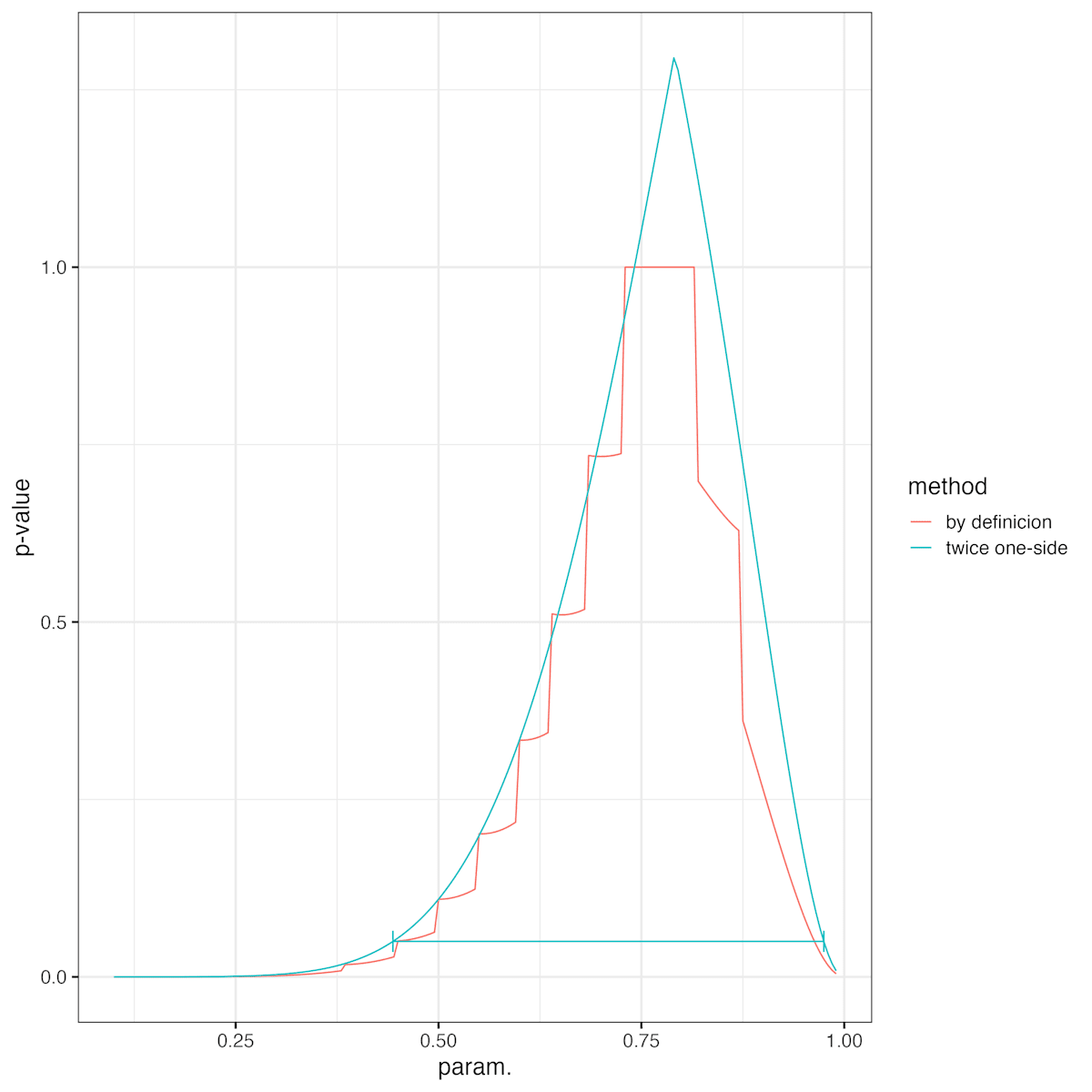
分布が左右対称のときは片側検定の p 値の2倍が両側検定の p 値と一致すると思うが, そうでないときは一致しない.
ところで binom.test の結果には Exact binomial test と書かれている.
> print(res0_b)

	Exact binomial test

data:  9 and 10
number of successes = 9, number of trials = 10, p-value =
0.02148
alternative hypothesis: true probability of success is not equal to 0.5
95 percent confidence interval:
 0.5549839 0.9974714
sample estimates:
probability of success 
                   0.9 
統計的仮説検定の場合の "Exact" は「サンプルサイズが大きいときにだけ成り立つような近似を使わない」程度の意味であることが多い.
（なのでもしかしたらこの記事の後の方に出てくるフィッシャーの正確確率検定もフィッシャーの直接確率検定くらいに訳すのがいいのかもしれないとも思ったが, 今回は見送り.）
このような exact test は確率分布の数だけ考えられるが, 二項検定以外に比較的よく使われるものが次のポアソン検定とフィッシャーの正確確率検定である.

 ポアソン検定ポアソン検定を行う poisson.test も同じ方針で実装されている.
pvfun0 <- function(r, x, tau){
  pu <- ppois(x-1, r*tau, lower.tail = FALSE)
  pl <- ppois(x, r*tau, lower.tail = TRUE)
  2*pmin(pl, pu)
}
rvec <- seq(0.01,3,by=0.01)
pv_p <- sapply(rvec, function(r)poisson.test(8, 10, r = r)$p.value)
pv_p0 <- pvfun0(rvec, 8, 10)
res0_p <- poisson.test(8, 10)

ggplot(data = NULL)+
  geom_line(aes(x=rvec, y=pv_p, colour="by definicion"))+
  geom_line(aes(x=rvec, y=pv_p0, colour="twice one-side"))+
  geom_errorbarh(aes(y=0.05, xmin = res0_p$conf.int[1], xmax=res0_p$conf.int[2], colour="twice one-side"),
                 height=0.03)+
  theme_bw(16)+
  labs(x="param.", y="p-value", colour="method", linetype="method")
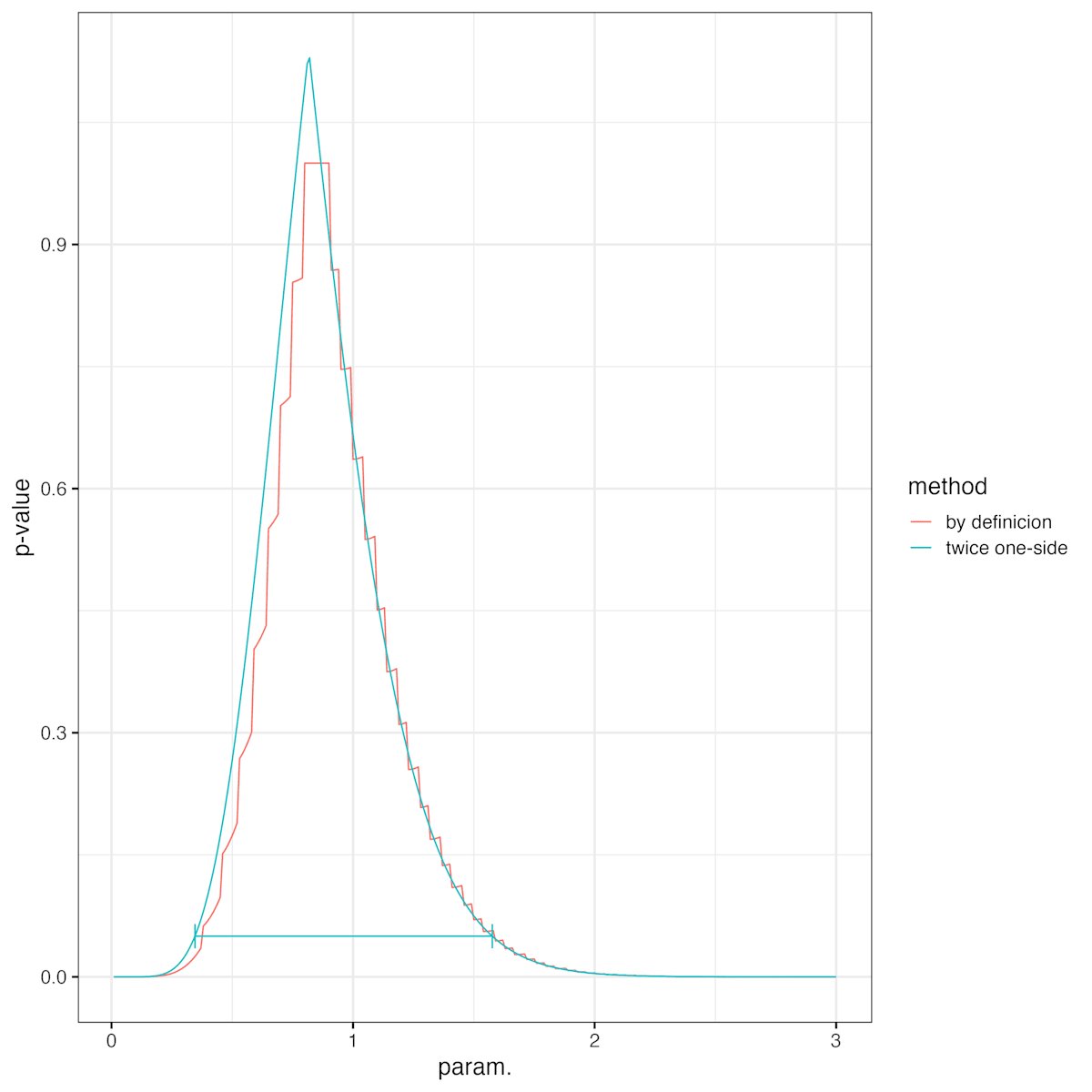
補足：
\mathrm{binom}(n, p) をサイズ n, 成功確率 p の2項分布, \mathrm{pois}(\lambda) を平均 \lambda のポアソン分布とすると, binom.test(x = 8, n = 10, p = 0.5) は

x \sim \mathrm{binom}(10, 0.5)
poisson.test(8, 10, r) は

x \sim \mathrm{pois}(10r)
として確率を計算している. 2項分布の方は上限が決まっているがポアソン分布の方は10が上限というわけではない.

 フィッシャーの正確確率検定フィッシャーの正確確率検定を行う fisher.test も同じ方針で実装されている（2×2の表，オッズ比，相対危険度）が, そもそも帰無仮説のオッズ比を直接指定できる形式になっていない…….
フィッシャーの非心超幾何分布（Fisher's noncentral hypergeometric distribution - Wikipedia）は MCMCpack というパッケージにあったのでこれを使う.
confint_fisher <- function(X, level=0.95){
  rs <- rowSums(X)
  cs <- colSums(X)
  alpha <- 1-level
  testfun_up <- function(phi){
    pall <- MCMCpack::dnoncenhypergeom(x = NA, cs[1],cs[2],rs[1], exp(phi))
    i <- match(X[1,1],pall[,1])
    pv <- sum(pall[i:nrow(pall),2])
    pv-alpha/2
  }
  testfun_low <- function(phi){
    pall <- MCMCpack::dnoncenhypergeom(x = NA,
                                       cs[1],cs[2],rs[1], exp(phi))
    i <- match(X[1,1],pall[,1])
    pv <- sum(pall[1:i,2])
    pv-alpha/2
  }
  res_u <- uniroot(testfun_up, lower = -10, upper = 10)
  res_l <- uniroot(testfun_low, lower = -10, upper = 10)
  list(oddsratio=c(exp(res_u$root),exp(res_l$root)))
}

X <-matrix(c(12,5,6,12), nrow=2)
resf <- fisher.test(X, conf.level = 0.95)
片側検定の p 値の2倍で両側検定の p 値を定義すると fisher.test の返す信頼区間と一致することがわかった.
> print(resf$conf.int)
[1]  0.9465292 25.7201471
attr(,"conf.level")
[1] 0.95
> print(confint_fisher(X))
$oddsratio
[1]  0.9465291 25.7205551
exact2x2 パッケージの exact2x2 関数は帰無仮説のオッズ比を指定できるし p 値と信頼区間が整合するよう書かれているので基本的にこちらを使うといいと思う.

 追記: フィッシャーの非心超幾何分布フィッシャーの正確確率検定の紹介はWeb上にもいろいろなページがある.
しかしこの記事のように
「帰無仮説のパラメータを引数にして p 値を返す関数が書かれていれば, こんなふうにして信頼区間も得ることができ, 2つが整合する」
という方針だと, 帰無仮説がフィッシャーの非心超幾何分布のパラメータになっていることを明示していない解説は「こっち見といて」としにくい.
そこでフィッシャーの非心超幾何分布自体の説明も書いておくことにした. 人によって強調するポイントが違ったりするのも悪くはないだろう.
なんかの要因への曝露（ばくろ; 悪いこととは限らない）によって, ある疾病を持つかどうか調べたところ, 次のようなデータが得られたとしよう.



曝露あり
曝露なし


病気あり
x
y

病気なし
m-x
n-y

この表が得られる確率を計算する一つの方法として,次のような2項分布のモデルが考えられる.

x \sim \mathrm{Binom}(m, q)

y \sim \mathrm{Binom}(n, r)
k=x+y と置くことにし, 表の周辺度数（タテ・ヨコ合計）を固定したとき,

\begin{aligned}
p(x|m,n,k,q,r) &\propto  p(k-x|n,r,x)p(x|m,q)\\
&\propto r^{k-x}(1-r)^{n-(k-x)} q^x(1-q)^{m-x}. \tag{1}
\end{aligned}
x, y それぞれのオッズを \omega _x = q/(1-q), \omega _y = r/(1-r), さらにオッズ比を \omega=\omega_x/\omega_y と書くことにすると,

\begin{aligned}
(1) &= \omega_y^{k-x}(1-r)^{n} \omega_x^x(1-q)^{m}\\
&=\omega^x \omega_y^{k}(1-r)^{n}(1-q)^{m}.
\end{aligned}
また k の分布は次のたたみ込みである.

p(k|m,n,q,r) = \sum_u p(y=k-u|n,r,x)p(x=u|m,q).
よって x に依存しない \omega_y^{k}(1-r)^{n}(1-q)^{m} の部分は分子・分母で消え,

\begin{aligned}
p(x|m,n,k,q,r) &= \frac{p(k-x|n,r,x)p(x|m,q)}{p(k|m,n,q,r)}\\
&= \frac{1}{\sum_u \binom {m}{u} \binom {n}{n-u}\omega ^{u}} {\binom {m}{x}}{\binom {n}{n-x}}\omega ^{x}
\end{aligned}
となる. これをフィッシャーの非心超幾何分布と呼ぶ（Fisher's noncentral hypergeometric distribution - Wikipedia）.
右辺を見ると q, r を指定しなくてもオッズ比 \omega を決めれば分布が一意に決まることがわかる.
上では \sum_u の u の範囲をあいまいに書いてしまったが, 注意が必要な場合もあるので注意してほしい.
また, 一般に確率の比が一致する確率分布は一致するの二項分布・二項分布でなく分割表のセルごとに独立なポアソン分布やカテゴリ数が 4=2\times2 の多項分布で考えても同じになる.
この説明はある程度この手の式変形に慣れてる人向けの説明になってしまっている自覚はあって, シミュレーションなどを通じて理解するようなこともできればいずれはやるたいと思っている.

 まとめ検定とか信頼区画というのはそんなもの, p 値と信頼区間のズレは誤差だと思って気にしないという方針もあり得ると思う.
しかし私の意見としては簡単に整合させられる部分は整合させておいた方がいいように思う.
帰無仮説のパラメータを引数にして p 値を返す関数が書かれていれば, こんなふうにして信頼区間も得ることができ, 2つが整合する:
pvfun <- Vectorize(FUN = function(mu0){
  binom.test(8, 10,  p=mu0)$p.value  
})
sol_ci <- rootSolve::uniroot.all(f = function(p){pvfun(p)-0.05}, interval = c(0.1,0.99))
print(sol_ci)
もちろん帰無仮説を動かしたときの p 値全体（p 値関数）をプロットしても良い.
curve(pvfun(x), 0.1, 0.99, n=1001)
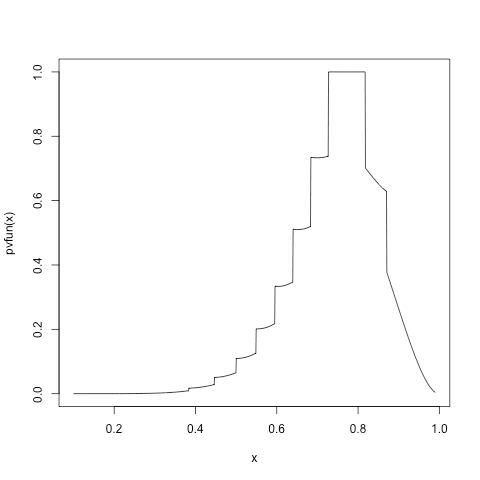
この記事で使用したRのコード全体はこちら：
https://github.com/abikoushi/Zenn_content/blob/main/R/exact_tests_r.R
おしまい.
	曝露あり	曝露なし
病気あり	$x$	$y$
病気なし	$m-x$	$n-y$
GitHubで編集を提案
要約

長い前置き: p 値について（再）入門するための手短な例

二項検定

ポアソン検定

フィッシャーの正確確率検定

追記: フィッシャーの非心超幾何分布

まとめ

Discussion
