尤度比検定, ワルド検定, スコア検定から定まる信頼区間：二項分布の例

導入

数理統計の本には良く「信頼区間は検定方式の反転によって得られる」というようなことが書かれている．

と，言うときにいま僕が手元で参照しているのは 『現代数理統計学の基礎』（久保川達也, 共立出版） だが, これ以外にも表紙のどこかに「数理統計学」と入っているような本には同様のことが書かれていることが多いと思う.

両側検定，

帰無仮説: $\theta = \theta_0$（1点）
対立仮説: $\theta \neq \theta_0$

の検定統計量 $T(X)$（標本$X$の関数）と棄却域$R(\theta_0)$（帰無仮説のパラメータに依存）から，

$$P_{\theta_0}(T(X) \in R(\theta_0)) = \alpha$$

とできるなら，

$$P_{\theta_0}(T(X) \in R^c(\theta_0)) = 1-\alpha$$

なので（$R^c(\theta_0)$ は受容域）これを $\theta_0$ について解くと，区間

$$C(X) = \{\theta_0|T(X) \in A(\theta_0)\}$$

が得られ，これは

$$P_{\theta_0}(\theta_0 \in C(X)) = 1-\alpha$$

となる．ちなみにこの $P_{\theta_0}(\theta_0 \in C(X))$ を 被覆確率 (covarage probability)という.

しかし, このあたりの話題は具体例を複数やらないとちょっとわかりにくいかもしれない.

関連：ウィルコクソン検定から得られる信頼区間

ここでは1標本の二項分布という（実用性を失わない範囲でたぶん一番簡単な）モデルを題材に信頼区間を求めてみる.

地道に手計算してみる

準備

尤度に基づく方法を考える.

モデルを

$$X \sim \mathrm{Binomial}(n, \theta)$$

とする.

推定したい未知パラメータは $\theta \in [0,1]$ である.

このときこのモデルの対数尤度関数は

$$\ell(\theta) = X \log(\theta) + (1-X) \log(1-\theta) + \mathrm{Const.}$$

と書ける．$\mathrm{Const.}$ は自由パラメータ $\theta$ に依存しない定数で微分すると消える．

対数尤度関数をパラメータで1階微分した導関数をスコア関数と呼ぶ．

スコア関数 $S(\theta)$ は

$$S(\theta) = \frac{d}{d\theta}\ell(\theta) = X/\theta - (1-X)/(1-\theta).$$

これを0とおいて $\theta$ について解くことにより, 最尤推定量は

$$\hat \theta = X/n$$

と求まる.

さらに,　フィッシャー情報量を最尤推定量のサンプルサイズ $n$ の大きいときの分布（漸近分布）のために考えておく.

フィッシャー情報量 $I(\theta)$ は対数尤度関数の2階微分の期待値の符号反転である.

$$\begin{align*} I(\theta) &= -E\left[\frac{d^2}{d\theta^2}\ell(\theta)\right] \\ &= -(E[-X /\theta^2 - (1-X)/(1-\theta)^2])\\ &= -n(-1/\theta - 1/(1-\theta))\\ &= \frac{n}{\theta(1-\theta)}. \end{align*}$$

尤度比検定

帰無仮説 $\theta=\theta_0$, 対立仮説 $\theta \neq \theta_0$ の尤度比検定では $\theta = \theta_0$ と固定した自由パラメータが0個のモデルと, 自由パラメータが1個のモデルで尤度の比の対数の2倍が自由度 $1-0 = 1$ のカイ二乗分布に従うことを利用する.

検定統計量は

$$T(X) = 2(\ell(\hat \theta) -\ell(\theta_0))$$

で, これが自由度1のカイ二乗分布の上側確率 $\alpha$ を与える点以下の範囲の $\theta_0$ が信頼区間である.

しかし閉じた形では求まらなかった.

Wald 検定

帰無仮説 $\theta=\theta_0$, 対立仮説 $\theta \neq \theta_0$ の Wald 検定は検定統計量

$$T(X) = |\hat \theta - \theta|\sqrt{I(\hat \theta)}$$

が帰無仮説の下で漸近的に標準正規分布にしたがうことを利用する．すなわち, 帰無仮説の下で

$$P_{\theta_0}(T(X) < z_{\alpha/2}) = 1-\alpha$$

ここで $z_{\alpha/2}$ は標準正規分布の上側確率 $\alpha/2$ を与える分位点である.

信頼区間はこれを $\theta_0$ について解くことで,

$$C(X) = [C_{-}, C_{+}]$$

と求まる.

ただし,

$$C_{-} = \hat \theta - z_{\alpha/2}\sqrt{\hat \theta(1 - \hat\theta)/n},$$

$$C_{+} = \hat \theta +z_{\alpha/2}\sqrt{\hat \theta(1- \hat\theta)/n}$$

とした.

スコア検定

帰無仮説 $\theta=\theta_0$, 対立仮説 $\theta \neq p_0$ のスコア検定は検定統計量

$$T(X) = |S(\theta_0)|/\sqrt{I(\theta_0)}$$

が帰無仮説の下で漸近的に標準正規分布にしたがうことを利用する.

この場合について書き下すと,

$$T(X) = \sqrt{n} \, \frac{|\hat \theta - \theta_0|}{\sqrt{\theta_0(1- \theta_0)}}.$$

$T(X) \le z_{\alpha/2}$ となる（受容域に入る）のは,

$$(\hat \theta - \theta_0)^2 < z_{\alpha/2}^2 \,\frac{\theta_0(1- \theta_0)}{n}$$

のときである.

この不等式は次のようにも書ける.

$$\left(1+\frac{z_{\alpha/2}^2}{n}\right)\theta_0^2 - 2\left(\hat\theta\theta_0 + \frac{z_{\alpha/2}}{n}\right)\theta_0 + (\hat \theta)^2 \le 0$$

なので $\theta_0$ について解くことは2次方程式の解を求めることであり, いくらかの計算の後,

$$C(X) = [C_{-} , C_{+}]$$

ただし,

$$C_{-} = (1+\frac{z_{\alpha/2}}{n})^{-1} \left( \hat \theta - \frac{z_{\alpha/2}^2}{2n} - z_{\alpha/2}\sqrt{\frac{z_{\alpha/2}}{4n^2} + \frac{\hat \theta (1-\hat \theta)}{n}} \right),$$

$$C_{+} = (1+\frac{z_{\alpha/2}}{n})^{-1} \left( \hat \theta + \frac{z_{\alpha/2}^2}{2n} + z_{\alpha/2}\sqrt{\frac{z_{\alpha/2}}{4n^2} + \frac{\hat \theta (1-\hat \theta)}{n}}\right)$$

とした.

Rによる実装例

尤度比検定

尤度比検定に基づく p 値を返す関数は例えば次のように書ける.

LRtest <- function(p,x,n){
  phat <- x/n
  lp <- 2*(dbinom(x, n, phat ,log = TRUE)-
             dbinom(x, n, p ,log = TRUE))
  pchisq(lp, 1, lower.tail = FALSE)
}

信頼区間は閉じた形では求まらなかったがせっかくコンピュータを使うので帰無仮説を動かして総当たり（0.005刻み）で p 値を計算してみよう.

set.seed(123)
n <- 20
x <- rbinom(1, n, 0.5)
print(x)
# [1] 9

z <- seq(0.01, 0.99, by=0.005)
pv_lr <- sapply(z, LRtest, x=x, n=n)
df_lr <- data.frame(p=z, pv=pv_lr, method="LR")

library(ggplot2)
ggplot(df_lr, aes(x=p, y=pv))+
  geom_line()+
  theme_bw(18)+labs(x="param.", y="p-value")

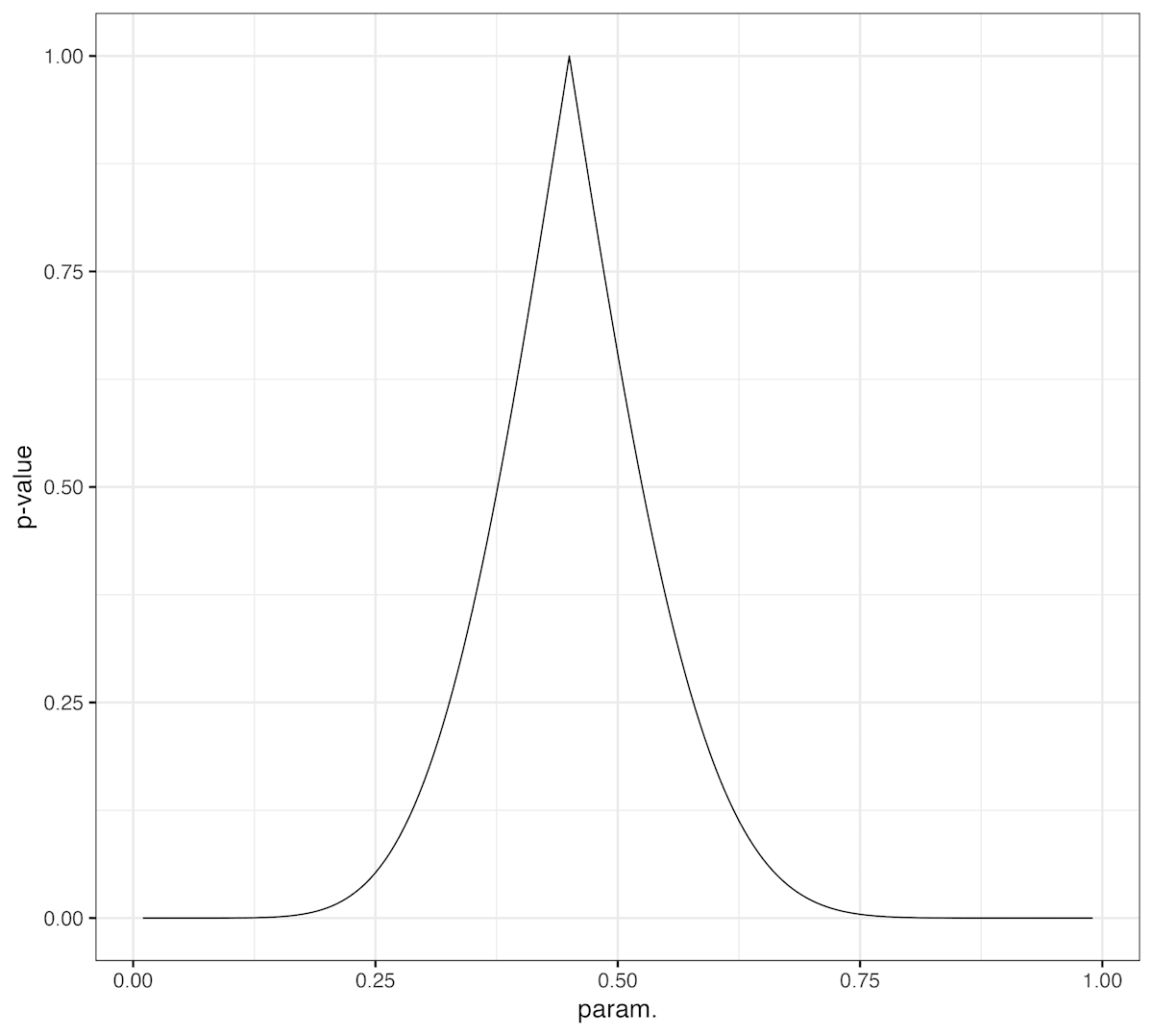
このグラフを例えば 0.05 の高さで切ってやれば95%信頼区間が求まる.

実は数値的に解くのはさほど大変ではない.

こんなふうだ:

library(rootSolve)
sol <- uniroot.all(function(p)LRtest(p,x,n)-0.05, c(0.1,0.8)) #0になる点を求める
print(sol)
#[1] 0.2479710 0.6641676
ggplot(df_lr, aes(x=p, y=pv))+
  geom_line()+
  geom_errorbarh(data = NULL, aes(xmin=sol[1], xmax=sol[2], y=0.05), height=0.03, colour="cornflowerblue")+
  theme_bw(18)+labs(x="param.", y="p-value")

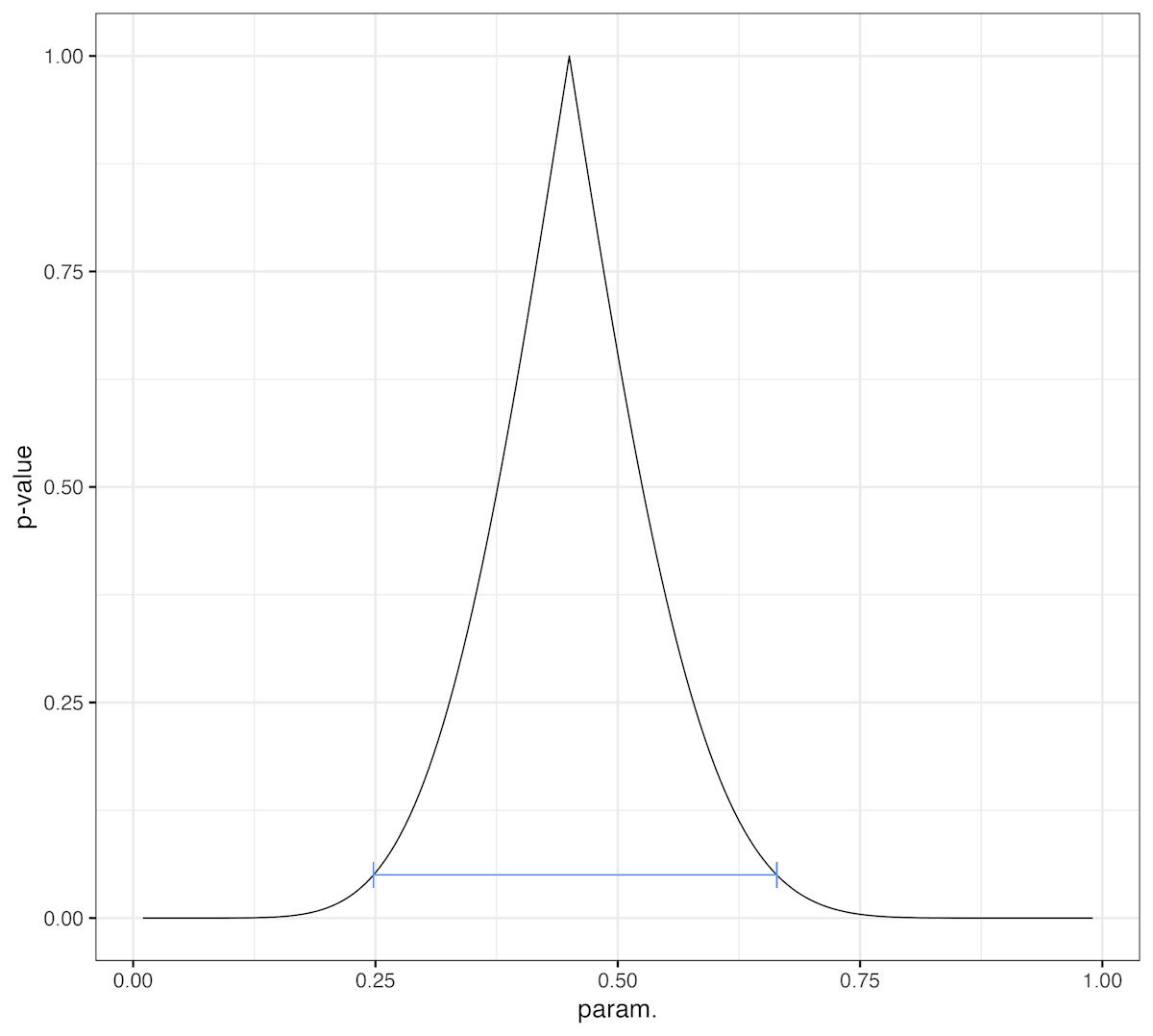
Wald 検定

Wald 検定に基づく p 値を返す関数は例えば次のように書ける.

waldtest <- function(p,x,n){
  phat <- x/n
  se <- sqrt(phat*(1-phat)/n)
  2*pnorm(abs(phat-p)/se, lower.tail = FALSE)
}

pv_w <- sapply(z, waldtest, x=x, n=n)
df_w <- data.frame(p=z, pv=pv_w, method="Wald")

abs で絶対値を取って片側だけ計算しているので2倍している.

スコア検定

R の prop.test はスコア検定に基づく．このことは次のように確かめられる.

set.seed(1234)
res_p <- prop.test(x, n, p = 0.5, correct = FALSE, conf.level = 0.95)

CI_score <- function(x, n, level){
  z <- qnorm(0.5*(1-level), lower.tail = FALSE)
  phat <- x/n
  t_1 <- phat+(z^2)/(2*n)
  t_2 <- z*sqrt(z^2/(4*n^2)+phat*(1-phat)/n)
  c((t_1 - t_2)/(1+(z^2)/n),
    (t_1 + t_2)/(1+(z^2)/n))  
}


print(CI_score(x,n,0.95))
print(res_p$conf.int)

> print(CI_score(x,n,0.95))
[1] 0.2581979 0.6579147
> print(res_p$conf.int)
[1] 0.2581979 0.6579147
attr(,"conf.level")
[1] 0.95

帰無仮説を動かしたときの p 値を 3 つの検定で比較してみよう.

pv_p <- sapply(z, function(p)prop.test(x, n, p = p, correct = FALSE)$p.value)
df_p <- data.frame(p=z, pv=pv_p, method="score")
df_pv <- rbind(df_lr,df_w,df_p)
ggplot(data = df_pv, aes(x=p, y=pv, colour=method, group = method, linetype=method))+
  geom_line()+
  scale_color_brewer(palette = "Set2")+
  theme_bw(16)+
  labs(x="param.", y="p-value", colour="method", linetype="method")
ggsave("proptest.png")

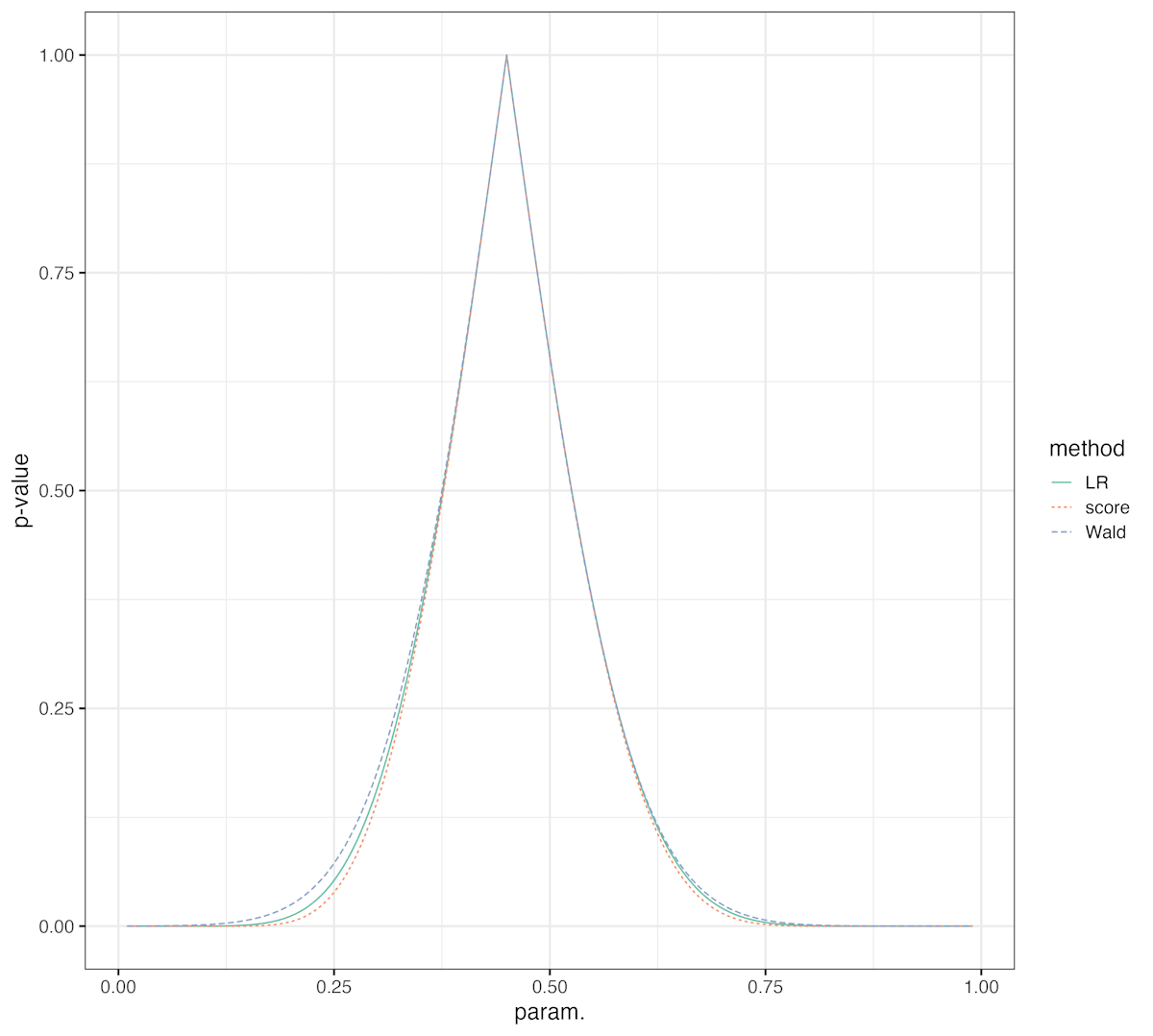
より大きい p 値が出やすい検定がより広い信頼区間を与える.

これだけではどの検定が良い検定かはまだわからない（次の記事に続く予定だったが記事をわけて書くのもそれはそれで面倒なのでこの記事に直接シミュレーションを追加した）.

しかし p 値が計算できれば検定も区間推定もできることがわかった.

ここまでのRのコードはこちら：

https://github.com/abikoushi/Zenn_content/blob/28b54a4fa9641c360d8df0fb285b29e8d5b9f78c/R/lr_wald_score.R

シミュレーション（追記 2025/08/08 ）

これからシミュレーションで信頼区間の被覆確率を調べる．

95％信頼区間を作ったら被覆確率も95％になってほしいが，上で求めた検定・信頼区間はサンプルサイズが大きいときに成り立つものである．有限個の標本での様子を調べるには乱数を使ってシミュレーションをするのが手っ取り早い．

導入のパートで述べた話に戻ると，有意水準 $\alpha$ で帰無仮説が棄却されない $\theta_0$ の範囲と　$100 \cdot (1-\alpha)$ ％信頼区間は同じであった．

つまり真のパラメータを帰無仮説にしておけば，信頼区間が真のパラメータを含むかどうかもわかる．

そこで次のように p 値を返す関数を書いた．

simfunc <- function(p_true, p_test, n, iter){
    x = rbinom(iter, n, p_true)
    pv_lr = LRtest(p_test, x, n)
    pv_wald = Waldtest(p_test, x, n)
    pv_score = sapply(x, function(x0){prop.test(x0, n, p = p_test, correct = FALSE)$p.value})
    pv_score_c = sapply(x, function(x0){prop.test(x0, n, p = p_test, correct = TRUE)$p.value})
    data.frame(lr=pv_lr, wald=pv_wald, score = pv_score,score_c = pv_score_c, p_true=p_true, p_test=p_test, n=n)
}

pv_score_c はイェイツの補正（説明は省略します．すみません）ありのスコア検定である．

早速10000回のシミュレーション（iter=10000）を行った結果を見ていく．横軸はシミュレーションで設定した真値である．

スコア検定（図の score, score_c）が一番名目上（nominal）の水準，95％に近い．

ところで，95％だけでなく色々な水準での信頼区間についても知りたいが，やはり導入のパートで述べた話に戻ると，これは p 値の分布を見れば十分である．

仮に横軸の有意水準で検定した場合，縦軸の確率で棄却されるということである．そして今回の場合，仮説検定で棄却されたことは信頼区間が真のパラメータを含まなかったことと同じである．

二項分布のパラメータの信頼区間については，尤度比検定やワルド検定よりはスコア検定から得られる信頼区間が良さそうなことがわかった．

シミュレーションについてのRのコードはこちら：

https://github.com/abikoushi/Zenn_content/blob/main/R/lr_wald_score_sim.R

ちなみに，ここで行ったシミュレーションに近い結果が，

Alan Agresti, Brent A. Coull. (1998). Approximate Is Better than "Exact" for Interval Estimation of Binomial Proportions. The American Statistician, 52(2) , pp. 119-126.

にも見られる．