ウィルコクソン検定から得られる信頼区間

導入

数理統計の本には良く「信頼区間は検定方式の反転によって得られる」というようなことが書かれている.

と, 言うときにいま僕が手元で参照しているのは『現代数理統計学の基礎』（久保川達也, 共立出版）だが, これ以外にも表紙のどこかに「数理統計学」と入っているような本には同様のことが書かれていることが多いと思う.

両側検定,

帰無仮説: $\theta = \theta_0$（1点）
対立仮説: $\theta \neq \theta_0$

の検定統計量 $T(X)$（標本$X$の関数）と受容域$A(\theta_0)$（帰無仮説のパラメータに依存）から,

$$P_{\theta_0}(T(X) \in A(\theta_0)) = 1-\alpha$$

とできるなら, これを $\theta_0$ について解くと, 信頼区間

$$C(X) = \{\theta_0|T(X) \in A(\theta_0)\}$$

が得られる.

しかし具体例を複数やらないとちょっとわかりにくいかもしれない.

そこでここでは2標本のウィルコクソン検定（ウィルコクソンの順位和検定）を使って信頼区間を求めてみる.

とりあえず計算してみる

Rでは関数 wilcox.test がウィルコクソン検定で, conf.int=TRUE とすると信頼区間を出力する.

この信頼区間が帰無仮説を棄却しない$\theta_0$の範囲と一致することを確かめよう.

library(ggplot2)
set.seed(123)
x <- rweibull(50,1.5) 
y <- rweibull(50,1.5)
U <- outer(x,y,"-") #全部の組み合わせで差を計算

sx <- sort(U[lower.tri(U, diag = TRUE)])
pv_w <- sapply(sx,function(m)wilcox.test(x, y, mu=m)$p.value)
df4p <- data.frame(sx=sx,pv=pv_w)

m <- median(U)
null_wilcox <- wilcox.test(x,y, conf.int = TRUE, conf.level = 0.95)

ggplot(df4p, aes(x=sx))+
  geom_step(aes(y=pv))+
  geom_rug(aes(x=sx), alpha=0.1)+
  annotate(geom="point", x=null_wilcox$estimate,y=1,
           colour="royalblue")+
  annotate(geom = "errorbarh",
           xmin=null_wilcox$conf.int[1],
           xmax=null_wilcox$conf.int[2],
           y=1-0.95,
           height=0.075,
           colour="royalblue")+
  theme_bw(18)+
  labs(y="p-value", x="U")

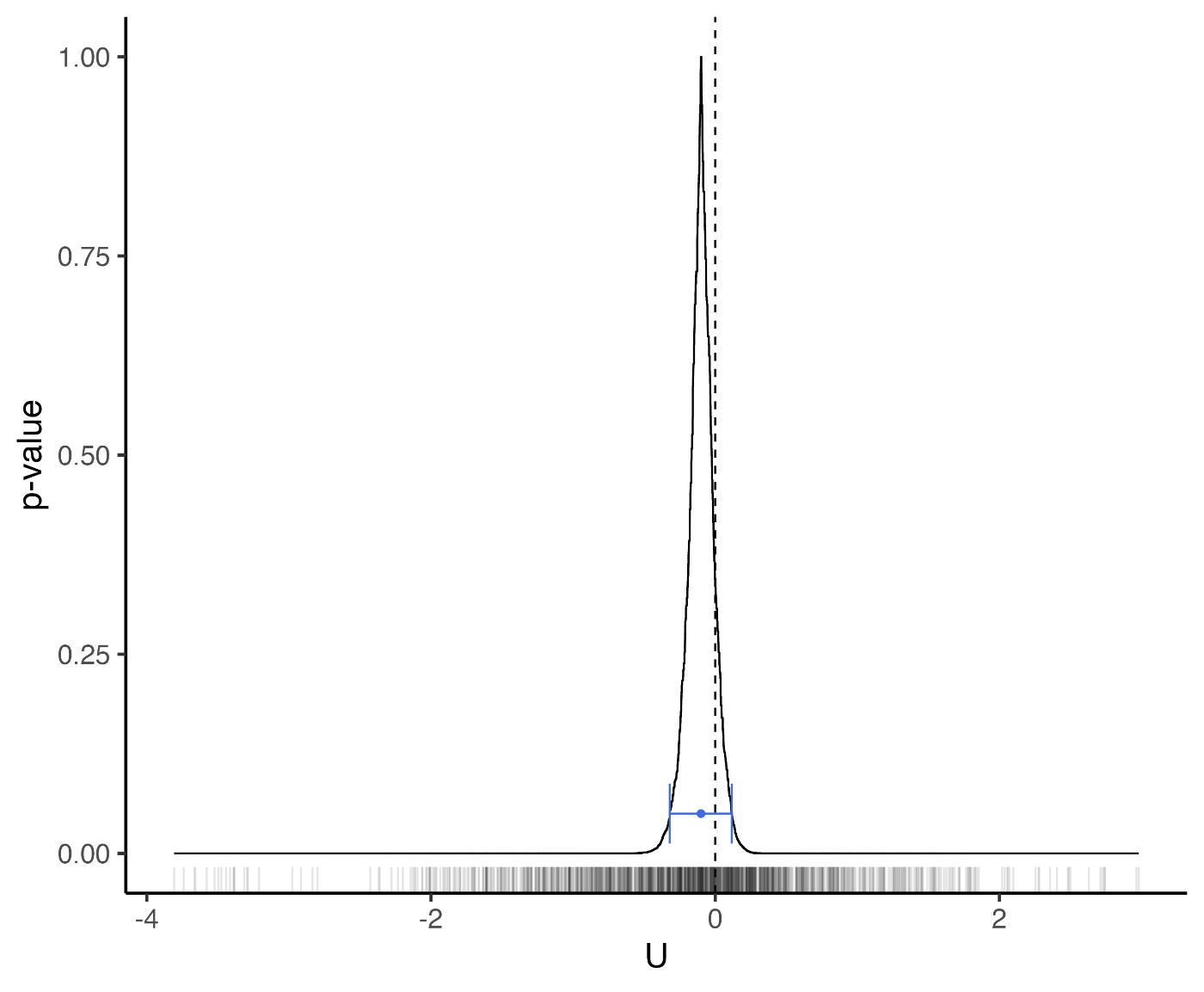
図の青いエラーバーが95％信頼区間, 曲線がp値.

ちなみに信頼区間の幅を0％まで縮めたもの（図中の丸いマーカー）はホッジス・レーマン（Hodges–Lehmann）推定量と呼ばれる.

結局, これが母集団のなにに対応する量を推定しようとしているのかを知るために, 改めてウィルコクソン検定を紹介する.

ウィルコクソン検定の紹介

2群, $X$ グループ: $X_i$ ($i=1,\ldots ,m$) と, $Y$ グループ: $Y_j$ ($j=1,\ldots ,n$)の比較を考える.

$X_i$ と $Y_j$ をまとめて小さい順に順位をつけると, もし $Y$ グループの方に大きい（小さい）値が多ければ $Y_j$ グループの順位も大きい（小さい）方に偏る.

どちらも同じ分布に従っているとすると $Y_j$ の順位は $\{1, 2, \ldots, n+m-1, n+m\}$ の範囲で一様分布（「同様に確からしい」）になる.

Rによる計算例:

#Rのコード
set.seed(123)
x <- rnorm(2)
y <- rnorm(2)
R <- rank(c(x,y)) #まとめて順位をつける

#最初の2列がyグループ
> round(rbind(c(x,y),R),2)
  [,1] [,2]  [,3]  [,4]
  1.56 0.07 -0.56 -0.23
R 4.00 3.00  1.00  2.00

Yグループの順位の取りうる値はすべて書き出せる.

(1,2), (1,3), (1,4)
(2,3), (2,4)
(3,4)

これより, Yグループの順位の合計もすべて書き出せる.

3, 4, 5
5, 6
7

この頻度を表にすると,

順位の合計	3	4	5	6	7
度数	1	1	2	1	1
確率	1/6	1/6	2/6	1/6	1/6

となる.

Rでシミュレーションしてみるとこの数え上げと同じ比の度数になることがわかる:

set.seed(1234)
W <- integer(10000)
for(i in 1:10000){
  x <- rnorm(2)
  y <- rnorm(2)
  R <- rank(c(y,x))
  W[i] <- sum(R[1:2]) #最初のn個がYの順位
}
barplot(table(W))

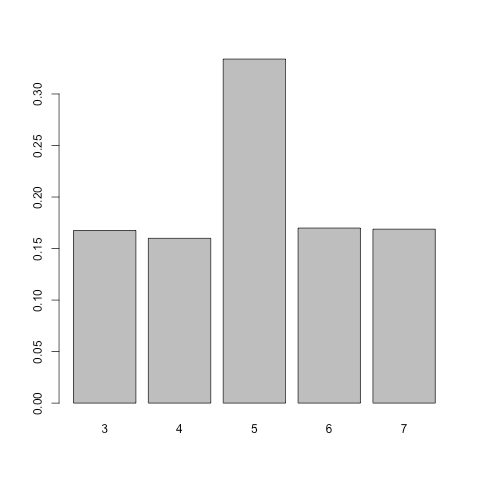
ちなみに, 次のように漸化式を作るともう少し現実的な時間で計算できる:

$$P(W=k)=p_{m,n}(k)=\frac{n}{m+n} p_{m,n-1}(k-m)+\frac{m}{m+n} p_{m-1,n}(k)$$

ここでは

$$W=Xグループの順位の合計 - \sum_{i=1}^m i$$

と変換して取りうる値の最小値が0になるようにしている.

R の wilcox.test が返す値もこの方式である.

この順位の合計を検定統計量にした検定を考えていく.

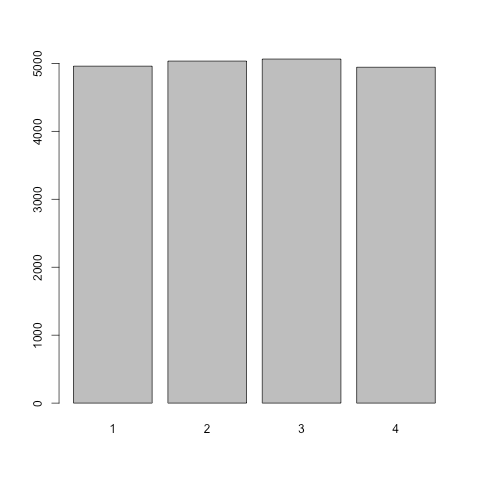
さて, Xグループの順位の分布は, 分布どうしで平均や中央値が同じとしても, 分布どうしの形状が違うときは一様にならない.

同じ分布でシミュレーション:

rlis1 <- vector("list", 10000)
for(i in 1:10000){
  x <- rnorm(2)
  y <- rnorm(2)
  R <- rank(c(y,x))
  rlis1[[i]] <- R[1:2] #最初のn個がYの順位
}

barplot(table(unlist(rlis1)))

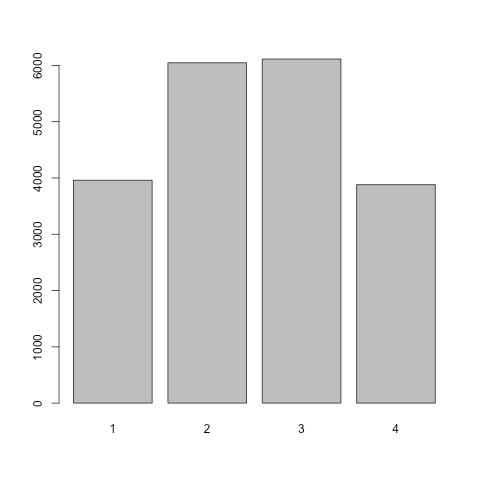
平均や中央値が同じで分散が違う分布でシミュレーション:

rlis2 <- vector("list", 10000)
for(i in 1:10000){
  x <- rnorm(2,0,1) #分散1
  y <- rnorm(2,0,2) #分散2^2
  R <- rank(c(y,x))
  rlis2[[i]] <- R[1:2] #最初のn個がYの順位
}

barplot(table(unlist(rlis2)))

ここで改めて標準的な両側検定の記法で書くと, $X_1, X_2, \ldots, X_m$, $Y_1, Y_2, \ldots, Y_n$ の2群の標本があり, $X_i$ の分布が $F(x-\mu)$（位置が $\mu$ だけずれている）, $Y_j$ の分布が $F(x)$ とするとき,

帰無仮説: $\mu = \mu_0$

対立仮説: $\mu \neq \mu_0$

を検定するのがウィルコクソン検定である.

ここまでの議論では暗に $\mu_0=0$ の場合を想定していたが, 一般の $\mu_0$ に対して検定するためには $X_i-\mu_0$ をXグループとすれば良い.

ところで, 検定統計量を

$$W = Xグループの順位の合計 - \sum_{i=1}^m i$$

としたが, この $W$ は

$$U_{ij} = (X_i - \mu_0) - Y_j$$

としたときの $U_{ij}>0$ となる $U_{ij}$ の個数と一致する.

（図は青線がマイナスでオレンジのチェックがプラス. $X$グループの順位が全部小さい方に偏っているときは $U_{ij}>0$ となる $U_{ij}$ の個数は0個,...,全部大きい方に偏っているときは $mn$個）

$U_{ij}$ の作り方から, ウィルコクソン検定による信頼区間は「2つの母集団から1つずつ標本を取り出して差を取ったときの中央値」を推定している.

これが知りたいことであった.

〇〇検定と名前のついているものはいっぱいありややこしいが, 個人的には「母集団のなにに対応する量を推定しているのか」という視点から理解しようとするといいと思う.

より強い言い方をすると, そこをスキップすると実質的に帰無仮説ロンダリングになってしまうのではないかと思う.

シミュレーション

差の中央値と中央値の差は一般には一致しないので「2群で中央値が異なる」ことの検定には使えない場合がある.

中央値が（ついでに分散も）同じ分布でシミュレーションしてみよう.

library(ggplot2)

#中央値
mu <- qexp(0.5)
print(qnorm(0.5,mu,1))

#差の中央値（数値積分による力技で確認）
conv <- function(x){
#たたみ込み
  integrate(function(y){dnorm(x+y,mu)*dexp(y)},-Inf,0)$value + 
  integrate(function(y){dnorm(x+y,mu)*dexp(y)},0,Inf)$value
}
conv <- Vectorize(conv)
m_root <- uniroot(function(x)integrate(conv,-Inf,x)$value-0.5, c(-1,0))

print(m_root$root)
#-0.1825963

#分散（数値積分による力技で確認）
v_e <- integrate(function(x)x^2*dexp(x), 0,Inf)$value - 
  integrate(function(x)x*dexp(x), 0,Inf)$value^2

v_n <- integrate(function(x)x^2*dnorm(x,mu,1), -Inf,Inf)$value -
  integrate(function(x)x*dnorm(x,mu,1), -Inf,Inf)$value^2

print(v_e)
#1
print(v_n)
#1

#繰り返し計算
n1 <-100
n2 <-100
pv_simfun <- function(n1,n2, mu, m){
  x1 <- rnorm(n1,mu,1)
  x2 <- rexp(n2)
  res_w <- wilcox.test(x1, x2, conf.int=TRUE)
  cp <- res_w$conf.int[1] < m & m < res_w$conf.int[2]
  data.frame(estimate=res_w$estimate,
             pv = res_w$p.value,
             cover = cp)
}

#手元のパソコンだと10秒くらいかかる
system.time({
  res <- lapply(1:10000, 
                function(i){set.seed(i);pv_simfun(25, 25, mu, m_root$root)})
  res <- do.call("rbind",res)
})
#  user  system elapsed 
#10.068   0.051  10.212 

#p値の経験分布
ggplot(res,aes(x=pv))+
  stat_ecdf()+
  geom_abline(slope = 1,intercept = 0, lty=2)+
  theme_bw()+labs(x="nominal", y="actual")
ggsave("wilcox_p.png")

print(round(mean(res$cover),2))
#0.95

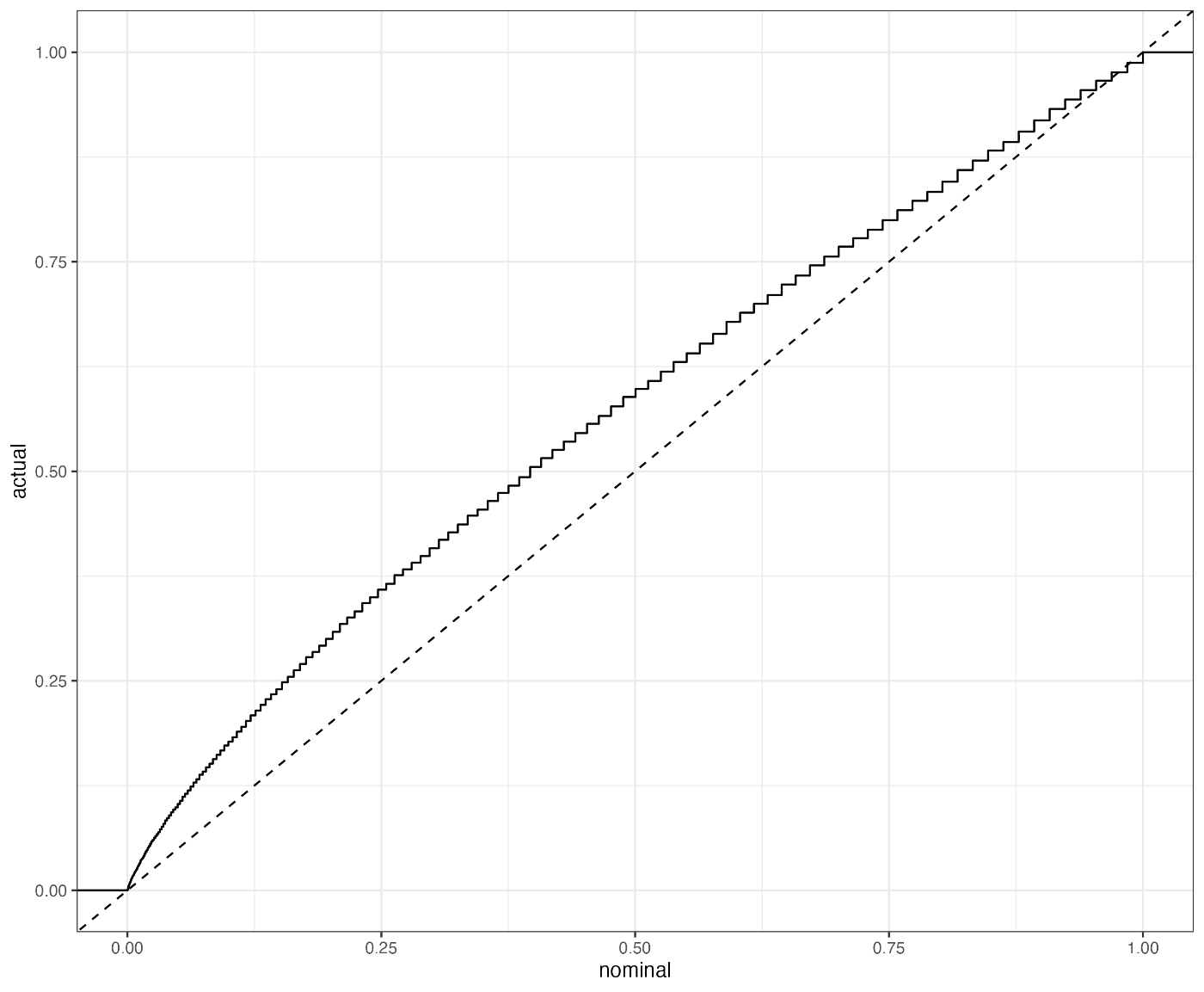
x軸の有意水準で棄却される確率がy軸なので, 中央値が同じ分布でも棄却されすぎていることがわかる.

一方で差の中央値の被覆確率については名目上の水準通りに保たれている.

> print(round(mean(res$cover),2))
[1] 0.95

このような場面でウィルコクソン検定を使って「中央値に差がある」という結論を出すのが, 上で「帰無仮説ロンダリング」と言ったものの例である.