これまでカーネルトリックについて思案してきた。それは絶妙な性質に基づいており、圏論的にほぐすことで興味深いつながりがいろいろ見えてくる。米田の補題もまたその一種であった。本記事ではフーリエ変換とのつながりを見、また圏論的フーリエ変換を見てみる。
ポントリャーギン双対
カーネルトリックの基本的な発想はデータ\Omegaを関数空間[\Omega, K]へ埋め込むことであった。もとより対象Aを調べるうえでその上の関数を考えること、すなわちHom函手\mathrm{Hom}(-,K)でHom送りにすることは数学の常套手段である。対象Aが何かよい数学的構造を持っており、その構造と整合する射(すなわち準同型)を考えると、射の集合\mathrm{Hom}(A,K)も制限を受けて何かしらのよい性質を獲得する。その例にポントリャーギン双対がある(記事が参考になる)。
Aがある代数構造(局所コンパクトハウスドルフ可換群)を持っている場合、円周(トーラス)\mathbb Tへの準同型射の集合\hat A \simeq \mathrm{Hom}(A,T)にもまたその代数構造が入り、指標群と呼ばれる。さらに\hat{\hat{G}}\simeq Gが成り立つ、というのがポントリャーギン双対のあらましである。
またG上のL^2関数全体L^2(G)に対し、指標群\hat G\simeq \mathrm{Hom}(G,T)の元がその基底を与える。たとえばG\simeq \mathbb Tのとき\hat G\simeq \mathbb Zとなり、指標は
\chi_n(\theta) = \mathrm{e}^{\mathrm i n \theta}
で与えられる。L^2(G)の元\phi, \psiに対しては
\phi(\theta) = \sum_{n} a_n\mathrm{e}^{\mathrm i n \theta},\quad
\psi(\theta) = \sum_{n} b_n\mathrm{e}^{\mathrm i n \theta}
のように分解でき、
\left<\phi,\psi\right> = \frac{1}{2\pi}\int \mathrm d\theta\, \bar \phi(\theta)\psi(\theta)
とすると
\sum_n \bar a_n b_n = \left<\phi,\psi\right>
が成り立つ。すなわちパーセヴァルの等式である。
G\simeq \mathbb Rのときは\hat Gも\mathbb Rであり、指標はおなじみの
\chi_k(x) = \mathrm e ^{\mathrm i kx}
である。これは\hat G\times G \simeq \mathbb R\times \mathbb R上の関数だがカーネル関数にはなっていない(再生性は成立しない)。その代わり積分変換
\mathcal F_\phi(k) = \int dx\,\mathrm e ^{\mathrm i kx}\phi(x)
を定義する。そしてやはりパーセヴァルの等式
\left<\phi,\psi\right> = \left<\mathcal F_\phi,\mathcal F_\psi\right>
が成り立つ。この内積がL^2(G)\times L^2(G)\rightarrow \mathbb Cなるカーネル関数を与えていると思えば、これもカーネルトリックと呼んで差し支えない。
圏論的フーリエ変換
profunctor や end については手前味噌だが他の記事を参照されたい。また本節の内容は書籍を参考にしている。
いま圏\mathcal C上の bi-profunctor P:\mathcal C\times \mathcal C\nrightarrow \mathcal Cに対し、次のように表記することにする。
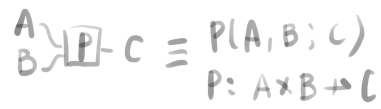
下のような函手J:1\rightarrow \mathcal C と合わせて次の性質を満たすとき、圏\mathcal C上のPromonoidal structure をこれらの組(\mathcal C,P,J)で定める。
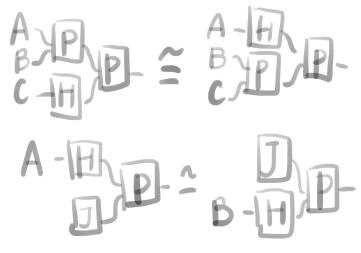
ここで Hはhomのことである。Pは結合律を満たす積に、Jは単位元に対応している。もちろんこれらの結合は end で定義されている。
いま以下の性質を満たすprofunctor K を乗法的カーネルと呼ぶ。
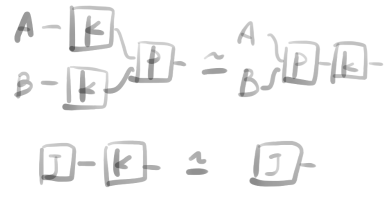
K-フーリエ変換
いま f: \mathcal C \rightarrow \mathcal{Sets}に対し乗法的カーネルKによる変換
\mathcal F_K[f] : X \mapsto \int^A K(A,X)\otimes fA
(すなわちKan拡張\mathrm{Kan}_よf)をK-フーリエ変換と呼ぶ。また双対K-フーリエ変換が
\mathcal F^\vee_K (g) : Y \mapsto \int_A [K(A,X),gA]
で定義される。*-autonomous 構造の下で
\mathcal F_K[f] \simeq \mathcal F^\vee_K[f^*]^*
が成り立つ。また*を持つ圏\mathcal Vでenrichされた圏\mathcal Cにおいて、函手f,g:\mathcal C\rightarrow \mathcal Vに対する内積を
\left< f,g\right> = \int^A fA^*\otimes gA
で定める。すると圏論的パーセヴァルの等式
\left< f,g\right> \simeq \left<\mathcal F_K[f],\mathcal F_K[g]\right>
が成立する。Dayは量子論への応用を期待しているようである。
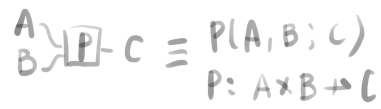
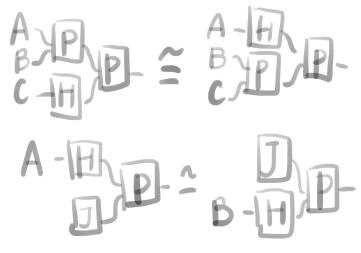
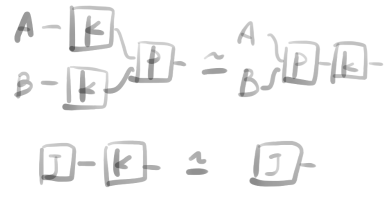
Discussion