この記事は圏論のprofunctorとendおよび文献を参考にHaskell で使われるOpticやLensを学んだ備忘録である。とくにLens のいくつかの定式化、すなわちexistential / profunctor / van Laarhoven encoding を見ていく。
profunctor とは
profunctor F:\mathcal C\nrightarrow \mathcal Dとは函手
\mathcal C^{op} \times \mathcal D \overset{F}\longrightarrow \mathcal{Sets}
のことである。それはHom函手の一般化になっている。集合論でいえばHomが写像を与えるのに対し、profunctorは関係を与える。関係は一対多の対応を許すのであった。Homは合成を持つが、profunctorにもその類似が定義できる。そのためにendが要る。
end とは
双自然変換とwedge
函手P,Q: \mathcal C^{op} \times \mathcal C \rightarrow \mathcal Dを考える。\mathcal Cの射 f:C\rightarrow C'は\mathcal Dで以下の図式を誘導する。
P(C,C) \xleftarrow{P(f,C)} P(C',C) \xrightarrow{P(C,f)} P(C',C')
Q(C,C) \xrightarrow{Q(C,f)} Q(C,C') \xleftarrow{Q(f,C)} Q(C',C')
これは、Data.Profunctorにおけるlmapとrmapに対応する。
class Profunctor p where
dimap :: (a -> b) -> (c -> d) -> p b c -> p a d
dimap f g = lmap f . rmap g
lmap :: (a -> b) -> p b c -> p a c
rmap :: (b -> c) -> p a b -> p a c
ここで双自然変換(dinatural transformation)\alpha: P\Rrightarrow Q を射\alpha_C:P(C,C)\rightarrow Q(C,C)であり、\mathcal Cの射 f:C\rightarrow C'に対して以下の図式を可換にするものとする。

定数函手 \Delta _D について \Delta_D \Rrightarrow P を wedge,P\Rrightarrow \Delta_D を cowedge と呼ぶ。
end と coend
end とは終wedge
\mathrm{end}(P) \Rrightarrow P
である。またcoend とは始cowedge
P\Rrightarrow \mathrm{coend}(P)
ある。すなわち普遍性で定義される(co)wedge のことである。end と coend はそれぞれ積分記法を用いても書かれる:
\mathrm{end}(P) = \int_C P(C,C),\quad
\mathrm{coend}(P) = \int^C P(C,C)
end は equalizer として定義すると簡潔だがここでは割愛する。
end と profunctor の合成
profunctor p: A\nrightarrow B, q: B\nrightarrow C に対し合成 q\circ p: A\nrightarrow C をcoendで定義する。
(q\circ p)(A,C) = \int^B p(A,B)\times q(B,C)
profunctor は関係に対応すると上で述べた。合成については以下の定義と対応する。
(x,z) \in S\circ R = \exist y \in Y \mathrm{~s.t.~} (x,y) \in S \wedge (y,z) \in R
物理学をやった方は伝搬関数を思い浮かべるだろう。記法のもともとのオリジンはそこにあると思われる。
(G\circ F)(x,z) = \int dy G(x,y) F (y,z)
代数幾何をやった方は代数対応が類似の概念として挙げられるかもれない。もう少し簡単な例を示しておこう。関数の合成
\left(\begin{split}
&y = f(x) = x^2 \\
&z = g(y) = y + a
\end{split}\right)
\rightarrow \left(z = (g\circ f)(x)= x^2 + a\right)
は入力と出力をつなげていくだけだが、関数と解釈すると多価になるような曲線についても、Groebner 基底などを用いた変数除去を行うことで同様の「合成」をすることができる。
\left(y^2 = x^3 -x , y^4 = z\right)\rightarrow \left(z= \left(x^3 - x\right)^2\right)
だから coend は2回現れる変数の除去、「インテグレート(トレース)・アウト」のイメージで理解することができる(論理式上は存在量化子もそのような機能を持つ)。なお有名な忍者米田の補題は
F\simeq \int ^C FC \times \mathcal{C}(-,C), \quad
G\simeq \int _C \mathcal{Sets}(\mathcal{C}(C,-),GC),
と書かれる。coend は積構造におけるインテグレート・アウトを、endは冪構造におけるインテグレート・アウトに対応している。忍者米田の補題から見ると米田埋め込みはいわば恒等演算子である。
Profunctor Optics
end を用いると次のような構造を現すことができる。
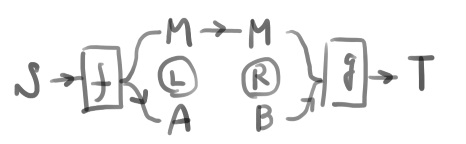
この考え方は先述の文献のほかサーベイ論文でも述べられている。
上の構図に基づき以下の式をOpticと定義する。
\mathbf{Optic}_{\text{\textcircled L},\text{\textcircled R}}((A,B),(S,T))
= \int^{M\in \mathcal M} \mathcal{C}(S,M\text{\textcircled L} A)\times \mathcal{D}(M\text{\textcircled R} B,T)
ここで圏 \mathcal C, \mathcal D にモノイド圏\mathcal Mが作用しており、\text{\textcircled L},\text{\textcircled R}はそれぞれ\mathcal C, \mathcal Dへの作用を表す。
文献には多くの具体例が表にまとめられている。
Opticの圏
\mathbf{Optic}_{\text{\textcircled L},\text{\textcircled R}}((A,B),(S,T)) をprofunctor (S,T)\nrightarrow (A,B) と見なすと、Optic の結合

が定まり、Opticの圏\mathrm{Optic}_{\mathcal{C},\mathcal D}が定義される。詳細は論文に記載されている。
Profunctor Encoding
Opticのこの定式化は profunctor representation ないしは existential encodingと呼ばれている。\mathcal C = \mathcal Dで\mathcal{Sets}圏を考えるとき、\mathcal C^{op}\times \mathcal Cと同じ対象を持ち、
\mathbf{D}_\mathcal C ((A,B),(S,T)) = \int^{M\in \mathcal M} \mathcal{C}(S,M\otimes A)\times \mathcal{C}(M\otimes B,T)
を射とする圏\mathbf{D}_{\mathcal C}において
\int_{P\in た(\mathcal C)} \mathcal{Sets}(P(A,B),P(S,T))
\simeq \mathbf{D}_\mathcal C ((A,B),(S,T))
が成り立つ(参考:n-Cat Caféの記事,論文)。これをprofunctor representation theorem と呼ぶ。この式がOpticのprofunctor encodingを与える。
ここで圏\mathcal{C}上の丹原圏た(\mathcal C)はprofunctor \mathcal C \nrightarrow \mathcal Cおよびある性質を持った持ち上げ(丹原構造)
\tau_A(X,Y) : P(X,Y) \rightarrow P(X\otimes A, Y\otimes A)
を対象とする圏である。射はそれらの間の自然変換を用いる。さらに丹原圏と\mathbf{D}_\mathcal Cに対して同型
た(\mathcal{C}) \simeq \mathcal{Sets}^{\mathbf{D}_{\mathcal C}}
が成り立つ(論文)。この辺りには普遍的な圏論的現象がありそうなのだがまだ感覚が掴めていない。
Lens
Lens は\mathcal W圏 \mathcal C, \mathcal Dに対し
\mathbf{Lens}((S,T),(A,B)) = \mathcal{C}(S,A)\times \mathcal D(S\bullet B,T)
で定義される。ここで\bulletは\mathcal Cの\mathcal Dへのモノイダルな作用 \bullet : \mathcal C \times \mathcal D \rightarrow Dである。(S,T)はデータ構造(オブジェクト)、(A,B)はそのプロパティに対応する。そして\mathcal{C}(S,A)はgetter、\mathcal D(S\bullet B,T)はsetterである。\bulletは異なる圏の対象の間に積を定義するために導入されたものであり、\mathcal C = \mathcal Dならば\bullet =\timesである。
ここで
\begin{split}
&\mathbf{Optic}_{\times,\bullet}((A,B),(S,T))
\\
& = \int^{C\in \mathcal C} \mathcal{C}(S,C\times A)\times \mathcal{D}(C\bullet B,T)
\\
& \simeq \int^{C\in \mathcal C} \mathcal{C}(S,C)\times \mathcal{C}(S,A)\times \mathcal{D}(C\bullet B,T)
\\
& \simeq \mathcal{C}(S,A)\times \mathcal D(S\bullet B,T)
\\
& = \mathbf{Lens}((S,T),(A,B))
\end{split}
が成り立つので、LensはOpticsの例になっている。ここで忍者米田の補題を用いている。
なお、LensといえばControl.Lensなどでは
type Lens s t a b = forall f. Functor f => (a -> f b) -> s -> f t
と定義されており、van Laarhoven encodingと呼ばれる。一方でOpticから導入される形式をexistential encoding と呼ぶ。
van Laarhoven encoding でのLensは
\mathbf{Lens}_{VL}(S,T,A,B) = \int_{F\in[\mathcal V, \mathcal V]} \mathcal V(A,FB)\otimes \mathcal V(S,FT)
を考えることになる。existential/van Laarhoven lensesの対応を見るにはより制限されたLinearLens
\mathbf{LinearLens}_{\otimes,\bullet}((A,B),(S,T))\simeq
\mathcal C(S,[B,T]\bullet A)
を考える必要がある。イメージとしては一般的なLensに圏論的な性質を添加して
\begin{split}
&\mathcal C(S,A)\times\mathcal D(S\bullet B,T)
\\
&\sim \mathcal C(S,A)\times \mathcal C(S,[B,T])
\\
&\sim\mathcal C(S,[B,T]\bullet A)
\end{split}
と束ねたものになっている。ここではモノイド積\otimesと内部hom[A,B]を持つ\mathcal Vモノイダル閉圏を考えている。
LinearLensももちろんOpticの例であり、van Laarhoven lens と LinearLens の等価性は忍者版の米田および余米田の補題から証明できる。
いま、existential encoding の Lensに対して\mathcal C=\mathcal Dでそれらが\mathcal{Sets}圏のとき、Opticの場合と同様に
\mathcal C(S,A)\times \mathcal C(S\times B, T)
\simeq \int_{P\in Cartesian} \mathcal{Sets}(P(A,B),P(S,T))
より、profunctor encoding の Lens が得られる。すなわち
type PLens a b s t = forall p. Cartesian p => p a b -> p s t
系の定義が得られる。ここでCartesian(ないしはstrong)profunctor とは A\nrightarrow BであってA\otimes C\nrightarrow B\otimes CやC\otimes A\nrightarrow C\otimes Bにリフト可能なものを言う。このあたりの話は論文で述べられている。

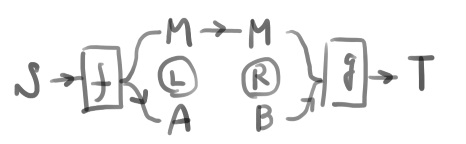

Discussion