カーネルトリックと米田の補題にて述べた内容は考え直してみれば普遍的に見られる現象であり、容易に一般化可能であった。本記事ではベクトル空間の例を見たのちにカーネルトリックが可能な条件を圏論的に特徴づけてみる。そして米田の補題を再考する。(続き)
ベクトル空間の例
前の記事で述べた対応が成立する最も身近と思われる例がベクトル空間である。
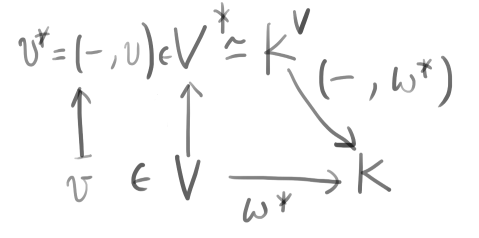
ここで(-,-)は内積(計量関数)、v^*=(-,v)はベクトルvの双対である。再生性は
w^*(v) = \left(v^*, w^*\right)
を、すなわち双対ベクトルの作用と内積の関係を意味する。そしてカーネルトリックは
\left(v, w\right) = \left(v^*, w^*\right)
すなわち内積をベクトル空間で計算しても双対ベクトル空間で計算してもよいということである。
圏論的な特徴づけ
再生性条件
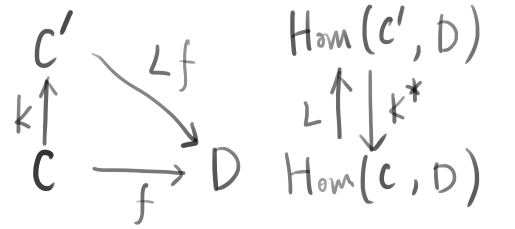
いまデータ対象Cと特徴量対象C'を考える。特徴量写像k: C\rightarrow C'およびリフトL:\mathrm{Hom}(C,D)\rightarrow \mathrm{Hom}(C',D)が存在して、射f \in \mathrm{Hom}(C,D)に対し
が成り立つとき、これを再生性と呼ぶことにする。ここでk^*: \mathrm{Hom}(C',D)\rightarrow \mathrm{Hom}(C,D)は\mathrm{Hom}函手によるkの持ち上げk^*=\mathrm{Hom}(k,D)である。
カーネルトリック
いまこの圏に内部homとモノイド積が入っているとして、C'=D^Cとする(これは一般にべき対象の記号だがここでは内部homを指すのに用いる)。すると随伴
\mathrm{Hom}\left(C,D^C\right)\simeq \mathrm{Hom}(C\otimes C,D),
および
\mathrm{Hom}\left(D^C,D^{\left(D^C\right)}\right)\simeq \mathrm{Hom}\left(D^C\otimes D^C,D\right),
が存在し、カーネル射 k\in \mathrm{Hom}(C\otimes C,D)および積\left<-,-\right>_L\in\mathrm{Hom}\left(D^C\otimes D^C,D\right)が定義できる。そして以下の図式
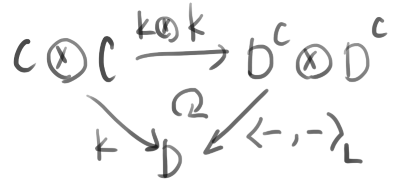
すなわちカーネルトリックが成立する。
まとめ
いまやカーネルトリックを圏論的に特徴づけることができたので、同様の図式が成立する場合にいつでもアナロジーを論じることができる。鍵となるのは再生性条件を与える
\mathrm{Hom}(C,D) ~\underset{L}{\overset{k^*}{\leftrightarrows}}~ \mathrm{Hom}(C',D)
の存在、そしてカーネルトリックを構成するための内部homおよび\otimesすなわちモノイド閉圏の構造である。
余談:Lawvereの不動点定理
このようにカーネルトリックを定式化すると、Lawvereの不動点定理という興味深いトピックに寄り道することができる。Cantorの定理やGödelの不完全性定理の骨格を一般化したものである。
いま対象CからC^Dへの射として全射であるような写像が存在するとする。すなわちC^Dの任意の元gについてあるt\in Cが存在する。ここでYanofskyによる次の図式を考えよう。
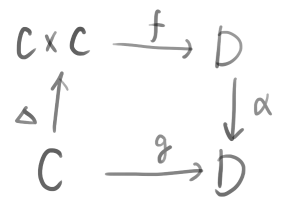
ここで\Deltaは対角射であり、fは
\mathrm{Hom}(C,C^D)\simeq \mathrm{Hom}(C\times C,D)
の元である。f(t,-)によってCの元tがC^Dに埋め込まれる。いま
なる写像を考える。ここで全射C\rightarrow C^Dが存在するので、このgにも対応するCの元t_0が存在する。すなわちf(t_0,t)=g(t)である。すると
g(t_0) = \alpha(f(t_0,t_0)) = \alpha(g(t_0))
となり、g(t_0)は\alphaの不動点となる。逆に不動点を持たない\alphaが存在するとき、全射C\rightarrow D^Cは存在しない。これがLawvereの不動点定理である。
Lawvereの不動点定理を使うと「すべてはCなのだ」とのたまう輩には反例を示すことができる。たとえばDとしてブール代数\mathbb{B}=\{\top,\bot\}を、\alphaとしてnotを与えてやればよい(Cとして「圏論」が入るとどうなるであろうか?)。
米田の補題再考
以上の話を踏まえて米田の補題を振り返ってみる。再生性のプロトタイプとなるのはKan拡張である。
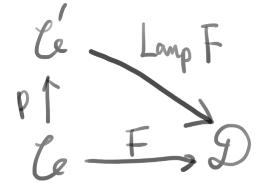
Kan 拡張において自然変換
F \Rightarrow p^* \mathrm{Lan}_p F
が存在する。ただし逆は一般に存在しないため、再生性も一般には成立しない。だがじつは\mathcal C'として\mathcal{Sets}^{\mathcal C^{op}}を、p として米田埋め込み函手よを考える、すなわち米田拡張を考えると再生性が成立する:
F \simeq よ^*\mathrm{Lan}_よ F
従って米田埋め込みはKan拡張において再生性が成立するための(おそらく十分)条件なのであった(追記:一般に充満埋め込み函手について成り立つ)。さらに\mathcal{D}=\mathcal{Sets} と取ることで、上の議論と同様にしてカーネルトリックが成立するのである。


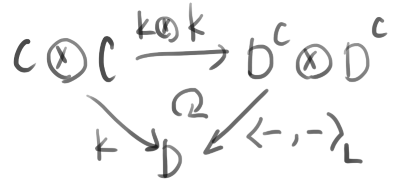
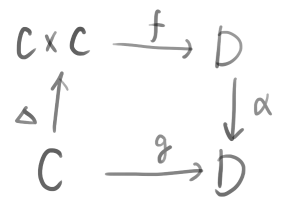

Discussion