データ分析や機械学習をやっているとカーネルトリックは避けて通れないと思われるが、その背景を確認しているとなんだか米田の補題に似ている気がしてくる。この記事はそのアナロジーの備忘録である。そして米田の補題はカーネルトリックである、と解釈してみる。何か手法を開発したり一般化する際に役立つかもしれない。(続き)
カーネルトリックの振り返り
あるデータ x,y,... を見通しよく分析するために、別の変数 f,g,...に置き換えて処理したい。そのような変数を一般に特徴量と呼ぶが、いまその特徴量として関数f(x),g(x),...を採用する。関数値ではなく関数そのものが特徴量である。この関数が再生核ヒルベルト空間\mathcal{H}の元であるとき、カーネル関数k(x,y)が存在して内積\langle -,-\rangle_{\mathcal H} について
f(x) = \langle k(-,x),f\rangle_{\mathcal H}
すなわち再生性が成り立つ。\phi_x(-) = k(-,x) にこれを適用すると
k(x,y) = \langle \phi_x,\phi_y\rangle_{\mathcal H}
すなわちカーネルトリックが成り立つ。つまり関数という無限次元の特徴量を用いつつ、計算の処理がそれらの間の内積\langle -,-\rangle_{\mathcal H}しか必要としないのならばカーネル関数k(x,y)をただ定義して用いればよい。
米田の補題の振り返り
米田の補題は次の図式で要約できる。

すなわち圏\mathcal{C}と集合の圏\mathcal{Sets}および函手F:C^{op}\rightarrow \mathcal{Sets}について
FA \simeq \mathrm{Hom}_{\mathcal{Sets}^{\mathcal C ^{op}}}(\mathrm{Hom}_{\mathcal{C}}(-, A), F)
が成り立つ。とくによ_A=\mathrm{Hom}_{\mathcal{C}}(-, A) とすると
\mathrm{Hom}_{\mathcal{C}}(A,B) \simeq \mathrm{Hom}_{\mathcal{Sets}^{\mathcal C ^{op}}}(よ_A, よ_B)
が成り立つ。
カーネルトリックを米田の補題流に
カーネルトリックのロジックを米田の補題流に描くと次のようになる。
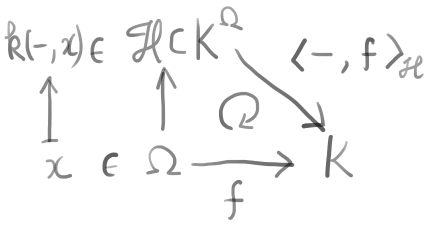
すなわちデータの対象\Omegaと特徴量f:\Omega\rightarrow K\in \mathcal Hに対し、つぎの対応がある。
| カーネルトリック |
米田の補題 |
| データ対象\Omega
|
圏\mathcal{C}
|
| 再生核ヒルベルト空間 \mathcal H
|
前層の圏\mathcal{Sets}^{\mathcal C^{op}}
|
| 特徴量f:\Omega \rightarrow K
|
函手F:\mathcal{C}^{op}\rightarrow \mathcal{Sets}
|
| カーネル関数k(-,-)
|
Hom函手 \mathrm{Hom}_{\mathcal{C}}(-,-)
|
| 内積\langle -,-\rangle_{\mathcal H}
|
Hom函手 \mathrm{Hom}_{\mathcal{Sets}^{\mathcal C^{op}}}(-,-)
|
米田の補題をカーネルトリック流に
再生核ヒルベルト空間はカーネルトリックを通じてデータ対象\Omegaを特徴量\mathcal H \subset K^\Omegaで理解することを可能にする。非自明な構造化データに対する例も知られているし、特徴量fがL^2(K)などより多くの性質を持った集合の元である場合には(圏論的にも)よい性質がいろいろ使える(Mercerの定理など)。
米田の補題もまた同様に、圏\mathcal{C}を前層の圏\mathcal{Sets}^{\mathcal C^{op}}に埋め込んで理解できることを保証している。実際、前層の圏は一般の圏にはない良い性質を持っている(nlabのRemarkを参照せよ)。圏\mathcal{C}がもっと構造を持っていれば(たとえばsiteであれば)より非自明な議論を展開することができる。

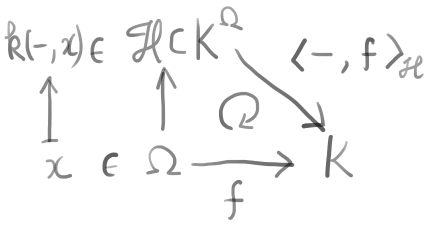
Discussion