TimesNet解説 Part2 アーキテクチャ

TimesNet解説のPart2です。Part1はこちら。

この記事は、TimesNet: The Latest Advance in Time Series Forecastingを参考に記述しています。英語が読める方はこちらを確認して下さい。

2. TimesNetのアーキテクチャ

2.1 アーキテクチャ

では、TimesNetのアーキテクチャを見てみましょう。

・TimesNetアーキテクチャ

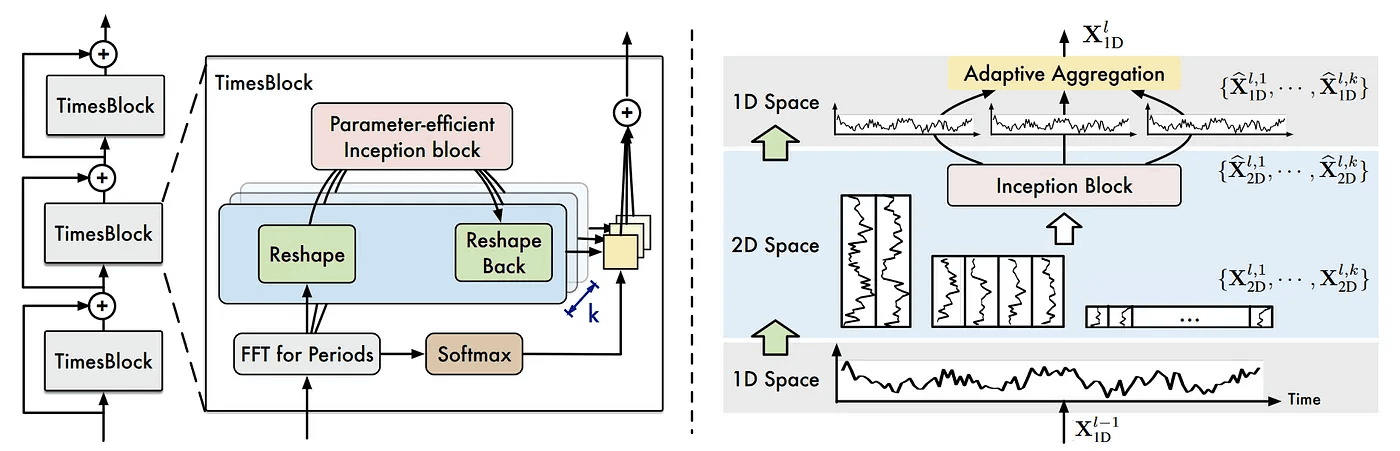
この図から、TimesNetは残差接続を持つTimesBlockが積み重ねられたものである事が分かります。

また各TimesBlockでは、時系列データの様々な周期性を見つけるために、最初にFFTを通している事が分かります。
次にFFTに通過後の一次元波形が二次元データとして再構成され、Inceptionブロックで学習および予測が行われます。最後にこの出力をAdaptive Aggregation(適応集約)を使用して一次元データに変更します。

ここからは、それぞれの処理について細かくみていきましょう。

2.2 期間内変動と期間間変動を捉える

著者らは、一次元のデータを二次元空間に変更して、期間内および期間間の変動を同時に捉えることを提案しています。

・期間内変動と期間間変動(intraperiod and interperiod variations)

この図は、様々な長さで分割された期間に対する期間内変動と期間間変動のイメージです。
赤い四角形は期間内のデータの変化、青い四角形は期間と期間の間のデータの変化を示しています。

この変動は二次元空間で表現され、期間間変動は垂直方向(青い矢印)、期間内変動は水平方向(赤い矢印)で表現されます。

2.3 期間の特定

上記では、時系列データを分割して二次元データを作成しました。では、このデータを分割する期間の長さ(period)はどのように決めれば良いでしょうか。

これは、フーリエ変換によって求める事ができます。

・二次元配列作成イメージ

図の左上に示すように、フーリエ変換は時系列データの各周波数成分の振幅の大きさを求める事ができます。(フーリエ変換についてはこちらでも解説しています)

FFTによって得られた振幅が最も大きい周波数が、最もデータの周期性と関係のあると考えられるため、この周期でデータの分割を行います。

2.4 TimesBolck

FFTによって得られた周波数で分割したデータを積み重ねて、2次元配列が作成されると、以下に示すようにデータがInceptionブロックに送られます。

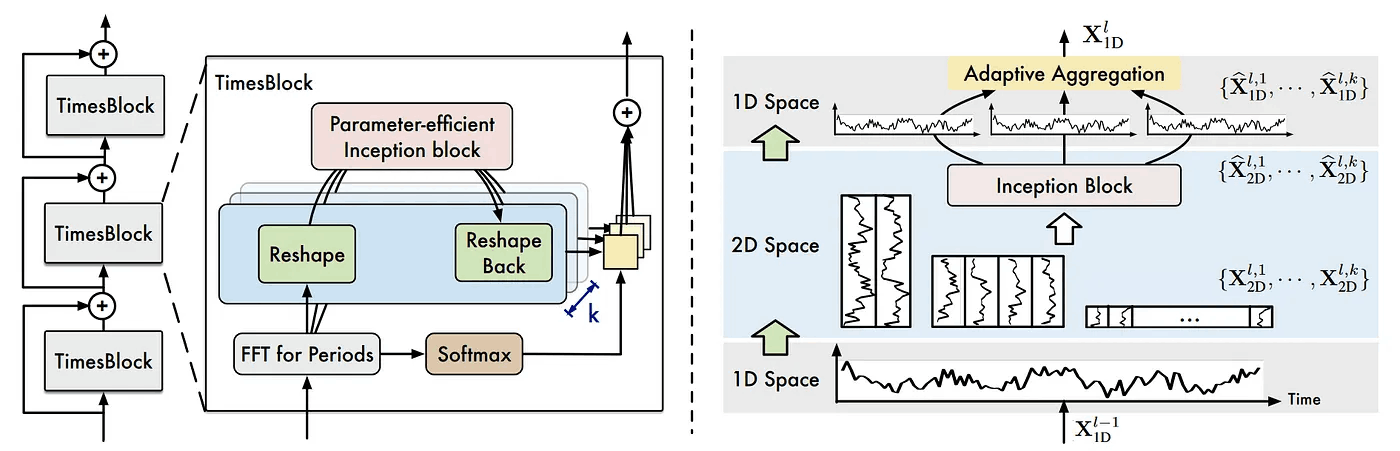
Inceptionモジュールの主なアイデアは、データを疎に保つことでデータを効率的に表現することです。これにより、計算効率を維持しながらNNのサイズを増やす事ができます。

これは、様々な畳み込みとプーリングを行った結果を結合することで実現されます。
TimesNetのアーキテクチャでは、Inceptionモジュールは以下のようになります。

・Inceptionモジュール

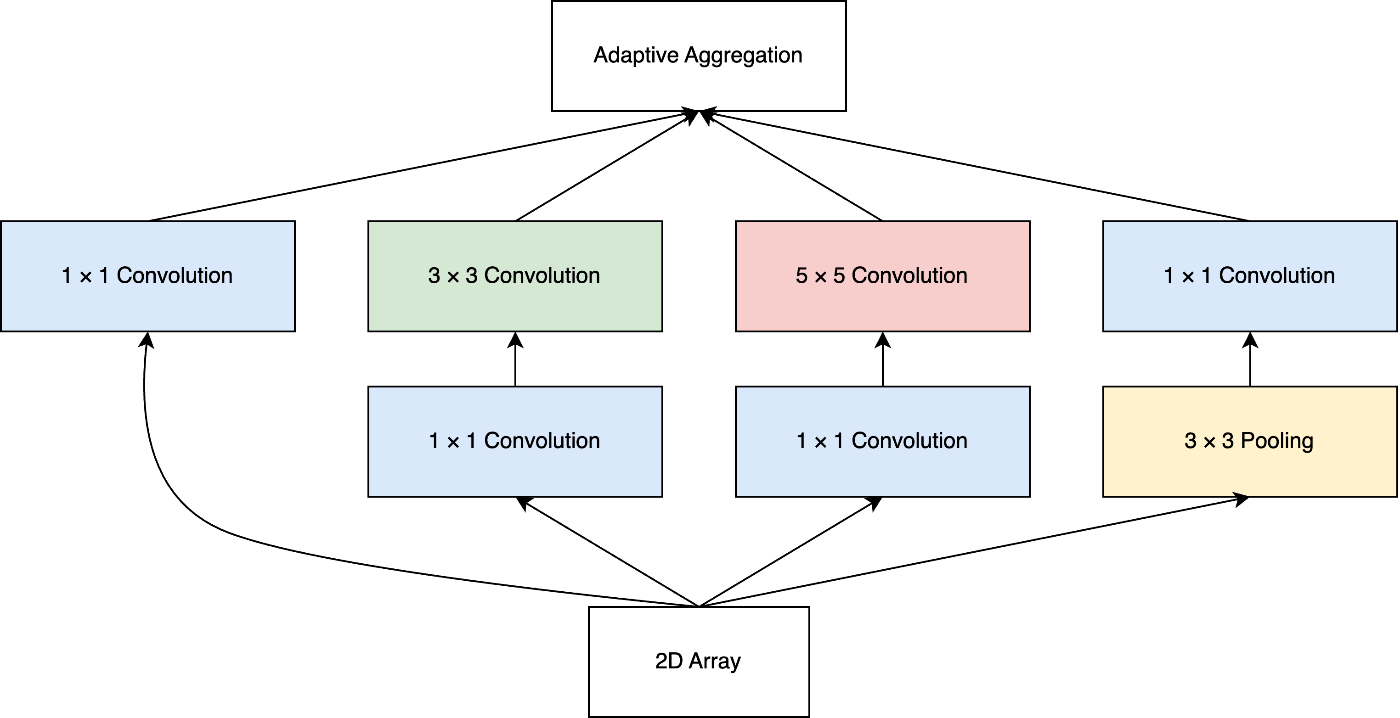
Inceptionモジュールでは畳み込みが行われるため、二次元配列が一次元配列に変換されます。

2.4.1 Adaptive Aggregation

TimesNetのInceptionモジュールの特徴として、Adaptive Aggregation(適応集約)があります。

TimesNetでは、周波数毎にFFTで得られる振幅の大きさが異なります。その違いによる各期間データの重要性を表現するために、Adaptive Aggregation(適応集約)が使用されます。
具体的には、Adaptive AggregationがInceptionモジュールからの特徴に加えて、「各期間の相対的な重要度」を利用できるように、FFTの出力もソフトマックス層に通された後、Adaptive Aggregationに渡されます。

このAdaptive Aggregationの出力が単一のTimesBlockの出力です。このTimesBlockが残差接続を伴って積み重ねられたものが、TimesNetモデルです。

2.5 結論

TimesNetはフーリエ変換を用いて分割すべき期間を見つけ出し、データを二次元配列にして、重み付けされた特徴を利用して学習を行うモデルでした。
また残差接続を利用することで、線型写像も学習する事ができるようになるため、より表現力が高くなっています。

まとめ

今回はTimesNetのアーキテクチャについて解説しました。
次回は実装を交えて解説を行う予定です。

参考

(1)TimesNet: The Latest Advance in Time Series Forecasting
(2)TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis
(3)Going Deeper with Convolutions(GoogLeNet)