フーリエ変換を理解する

フーリエ変換の備忘録。

1. フーリエ変換

フーリエ変換とは複雑な関数や現象を、三角関数に分解する手法である。

また非周期関数に対してフーリエ級数展開を行う際の主要な操作である。

1.1 フーリエ級数展開

"非周期関数へのフーリエ級数展開" をフーリエ変換と呼ぶ。(厳密には少し異なる。後述)
まずはフーリエ級数展開から説明するが、先に「1.9 フーリエ変換」から読み進めても良い。

・フーリエ級数展開
関数$f(x)$の特性が知りたいとき、より基本的な関数系$\{\varphi_0(x), \varphi_1(x), \varphi_2(x)...\}$で級数展開する。
式にすると以下

$f(x) = \sum\limits_{n=0}^{\infty} C_n \varphi_n$
※ $C_n$は調節用の係数

この$f(x)$が特定の条件を持つときの級数展開を、特別にマクローリン展開やフーリエ級数展開と呼ぶ。

条件

f(x)が次の条件を持つとき、それぞれ対応する関数系で級数展開を行うことができる。

1. $f(x)$が無限回微分可能な時
   $\{1, x, x^2, x^3,...\}$のようにxのべき乗で級数展開する(マクローリン展開)
   式にすると以下。
   $f(x) = \sum\limits_{n=0}^{\infty} \dfrac{f^{(n)}(0)}{n!} x^n$
   ※ $C_n = \dfrac{f^{(n)}(0)}{n!}$
   
   
   つまり、関数$f(x)$を「一つの関数のべき乗」の重ね合わせで表現できる
   
   
2. $f(x)$が周期関数の時
   $\{1, cosx, sinx, cos2x, sin2x,...\}$のように周波数の異なる三角関数で級数展開する(フーリエ級数展開)
   式にすると以下
   $f(x) = a + \sum\limits_{n=1}^{\infty} (a_n cosnx + b_n sinnx)$
   
   
   つまり、関数$f(x)$を「三角関数」の重ね合わせで表現できる
   ※$n=2\pi f$より周波数は$f=\dfrac{n}{2\pi}$

1をマクローリン展開、2をフーリエ級数展開と呼ぶ。

1.2 直交性

フーリエ級数展開は直交性の恩恵を受ける。
直交性: 自身以外との内積が0
内積：周期2πの関数$f(x)$,$g(x)$の内積は $\int^{\pi}_{-\pi} f(x)g(x) dx$で定義される

この時、異なる三角関数同士の内積、および1と三角関数の内積は常に0となる。この性質により、級数展開後の係数(フーリエ係数)の導出が簡単になる

1.3 フーリエ係数

・フーリエ級数展開
$f(x) = a + \sum\limits_{n=1}^{\infty} (a_n cosnx + b_n sinnx)$・・・(＊)
・フーリエ係数
上記の$a, a_n, b_n$

(＊)式の両辺に対して以下の操作を行うことで、フーリエ係数を導出できる。

1. $\int^{\pi}_{-\pi} f(x) dx$
2. $\int^{\pi}_{-\pi} f(x) cosmx dx (m=1,2,...)$
3. $\int^{\pi}_{-\pi} f(x) sinmx dx (m=1,2,...)$

1.2.3.の操作を(＊)の両辺に対して行なった結果
(左辺がフーリエ係数になるように式変形済)

1. $a = \dfrac{1}{2\pi} \int^{\pi}_{-\pi} f(x) dx$
2. $a_m = \dfrac{1}{\pi} \int^{\pi}_{-\pi} f(x) cosmx dx (n=mの場合以外はa_n=0)$
3. $b_m = \dfrac{1}{2\pi} \int^{\pi}_{-\pi} f(x) sinmx dx (n=mの場合以外はa_n=0)$

ここで$a=\dfrac{a_0}{2}$とすると$a=a_0$として$a_m$に内包できる。従って式1は式2にまとめられる。
この$a_m, b_m$をフーリエ係数と呼ぶ

1.4 フーリエ級数

以上をまとめてフーリエ級数を再度記述する。

・フーリエ級数
$\dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n cosnx + b_n sinnx)$・・・$(1)$
但し
$a_n = \frac{1}{\pi} \int^{\pi}_{-\pi} f(x) cosnx dx (n=0,1,2,...)$
$b_n = \frac{1}{\pi} \int^{\pi}_{-\pi} f(x) sinnx dx (n=1,2,...)$

$(1)$を、$f(x)$のフーリエ級数と呼ぶ。
※「$(1)=f(x)$」が成り立つか、つまりフーリエ級数が$f(x)$に収束するかどうかは別問題。フーリエ級数自体はいつでも定義できる。

この式が$f(x)$に収束する時、$f(x)= \dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n cosnx + b_n sinnx)$を解くことで、$f(x)$を三角関数の重ね合わせとして表現することができる。

1.5 不連続な関数への適用

フーリエ級数は連続した三角関数の重ね合わせであるが、区分的に滑らかな不連続な関数に対しても適用することができる。

区分的に滑らか

次の条件を満たす関数$f(x)$を区分的に連続であると言う
(1) 連続でない点が有限個
(2) 不連続点cにおいて左側極限$f(c-0)$と右側極限$f(c+0)$が存在する


さらにこの関数$f(x)$の導関数$f'(x)$が区分的に連続である時、関数$f(x)$を区分的に滑らかであるという。


この定義を満たす関数は多く存在するため、フーリエ級数展開は不連続な関数に対しても有用である。

・区分的に滑らかな不連続な関数へのフーリエ級数の適用
周期$2π$の周期関数$f(x)$が区分的に滑らかである時、$f(x)$のフーリエ級数は次のように収束する
$\dfrac{a_0}{2} + \sum\limits^{\infty}_{n=1} (a_n cosnx + b_n sinnx) = f(x)$   (連続な点)
                                                           $= \dfrac{f(x-0)+f(x+0)}{2}$   (不連続な点)

直感的には、不連続な関数へのフーリエ級数展開は、$f(x)$の不連続な点のみ中間の値を取る連続関数に収束する。

1.6 一般周期への適用

これまで、周期$2π$の関数に対するフーリエ級数のみを考えてきた。
周期を一般化して$2L$とした関数$f(x)$のフーリエ級数は以下のように導出される。

・一般周期の関数へのフーリエ級数の適用
まず周期$2L$が周期$2π$になるように変数変換。$x=\dfrac{L}{\pi}t$
関数$f(\dfrac{L}{\pi}t)$は周期$2π$なのでこれまでの手法が使える。フーリエ級数の式に当てはめてみよう。

・フーリエ級数
$\dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n cos\frac{nL}{\pi}t + b_n sin\frac{nL}{\pi}t)$
但し
$a_n = \dfrac{1}{\pi} \int^{\pi}_{-\pi} f(\frac{L}{\pi}t) cos\frac{nL}{\pi}t dt (n=0,1,2,...)$
$b_n = \dfrac{1}{\pi} \int^{\pi}_{-\pi} f(\frac{L}{\pi}t) sin\frac{nL}{\pi}t dt (n=1,2,...)$

ここで$dt$(周期$2π$)を$dx$(周期$2L$)に戻す。$x=\frac{L}{\pi}t$及び$dx=\frac{L}{\pi}dt$(直感的な変換)より

・フーリエ級数(一般周期Ver)
$\dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n cos\frac{n\pi}{L}x + b_n sin\frac{n\pi}{L}x)$・・・$(2)$
但し
$a_n = \frac{1}{L} \int^{L}_{-L} f(x) cos\frac{n\pi}{L}x dx (n=0,1,2,...)$
$b_n = \frac{1}{L} \int^{L}_{-L} f(x) sin\frac{n\pi}{L}x dx (n=1,2,...)$

式$(2)$が一般周期$2L$の関数に対するフーリエ級数である。

1.7 複素フーリエ級数

フーリエ級数は複素数で表すことができる。簡潔に記述でき、微積分計算が楽になるため頻繁に使用される。導出は以下

・複素フーリエ級数
$e^{i\theta} = cos\theta + isin\theta$ (オイラーの公式)
より
$\dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (a_n cosnx + b_n sinnx)$
$= \dfrac{a_0}{2} + \sum\limits_{n=1}^{\infty} (\dfrac{a_n - i b_n}{2} e^{inx} + \dfrac{a_n + i b_n}{2} e^{-inx})$
$\sim \sum\limits^{\infty}_{n=-\infty}C_n e^{inx}$・・・$(3)$
但し $C_n = \dfrac{1}{2\pi} \int^{\pi}_{-\pi} f(x)e^{-inx}dx$

※$\sim$: 連続点と非連続点によって結果が異なるため$=$の代わりに使用。連続点では=と同義
※$C_n$: 複素フーリエ係数。$a_0, a_n, b_n$を各積分式に展開すると導出される。

$(3)$式を複素フーリエ級数と呼ぶ。(周期$2\pi$)
これはフーリエ級数を複素形式で表したものである。

複素フーリエ係数Cnの性質

複素フーリエ係数$C_n$の性質

• $f(x)$が実関数(f(x)の値が実数)である時、$C_{-n} = C^{\ast}_n$(複素共役)が成り立つ。
  従って、各周波数について調べるときに、nが非負なもののみ計算すれば良い。

例えば後述のスペクトル解析の際にも、非負のみの解析で済む。

・一般周期の関数への複素フーリエ級数の適用
(3)式を一般周期に対応させると次のようになる
$f(x) \sim \sum\limits^{\infty}_{n=-\infty}C_n e^{i\frac{n\pi}{L}t}$・・・$(3')$
但し
$C_n = \dfrac{1}{2L} \int^{L}_{-L} f(x)e^{-i\frac{n\pi}{L}t}dx$

$(3')$式が対応周期を一般化した複素フーリエ級数である。(周期$2L$)

1.8 周波数スペクトル

・周波数スペクトル分析
スペクトルとは、波の周波数成分の強度分布を指す。

フーリエ級数による「波の三角関数への分解」を利用して、特定の周波数の波の大きさを視覚化したものが周波数スペクトル分析である。
つまり、どんな周波数の波が強く含まれているのか？を分析できる。

・フーリエ級数展開によるデータのスペクトル化

左の関数をフーリエ級数展開すると右の結果が得られた。これを離散スペクトルと呼ぶ。
左の関数には、強い20Hzの波と弱い5Hzの波が含まれることが分かる。
右図が周波数スペクトル(波の強度分布)に相当する。

1.9 フーリエ変換

・非周期関数へのフーリエ級数展開
これまで周期関数のみにフーリエ級数展開を行なってきた。
ここで非周期関数へのフーリエ級数展開を考える。

1.7の複素フーリエ級数$(2')$を再度示す($C_n$を展開した形)。$x$が重複するため$t$を使用するが特に意味はない
$f(x) \sim \sum\limits^{\infty}_{n=-\infty}\bigg[\dfrac{1}{2L} \int^L_{-L} f(t) e^{-i\frac{n\pi}{L}t} dt \bigg] e^{i\frac{n\pi}{L}t}$・・・$(3')$

ここで非周期関数を「周期が$\infty$の周期関数」と考えて複素フーリエ級数展開を行うと、次の式が導かれる。(長いため導出略。$\frac{n\pi}{L}=w$として区分求積法を用いる)

$f(x) \sim \int^{\infty}_{-\infty} \bigg[\dfrac{1}{2\pi} \int^{\infty}_{-\infty} f(t) e^{-iwt} dt\bigg] e^{iwt}dw$・・・$(4)$

この$(4)$式をフーリエの積分公式と呼ぶ。
式を見ると、$\Big[\Big]$内の関数に、$e^{iwt}$をかけて$-\infty$から$\infty$まで足し合わせている。
$e^{iwt}$は三角関数に変換できるため、$\Big[\Big]$を係数として三角関数の重ね合わせに分解できている。

従ってこのフーリエの積分公式が非周期関数へのフーリエ級数展開に相当する。

フーリエの積分公式が成立する条件

成立条件

1. $f(x)$が$(-\infty, \infty)$で区分的に滑らか
2. $(-\infty, \infty)$において$|f(x)|$が積分可能

・フーリエ変換
フーリエの積分公式における$\Big[\Big]$内の操作をフーリエ変換と呼ぶ。これは$\mathcal{F}()$と表記される。
$\mathcal{F}(f(t)) = \dfrac{1}{2\pi} \int^{\infty}_{-\infty} f(t) e^{-iwt} dt$・・・($f(t)$のフーリエ変換)
従って
$f(x) \sim \int^{\infty}_{-\infty} \mathcal{F}(f(t)) e^{iwt}dw$・・・$(4)$
※$\mathcal{F}()$: 関数$f(t)$に対して$e^{-iwt}$をかけて無限で積分する操作。$\dfrac{1}{2\pi}$は整合性のためであまり意味はない。

フーリエの積分公式を、フーリエ級数展開のように考えると、$\Big[\Big]$内の値はフーリエ係数に相当する。つまり、入力関数を、特定の周波数の波の強さに対する係数のような性質を持つ関数に変換する操作がフーリエ変換である。

少し難しいため補足すると、フーリエ級数展開では特定の周波数に対する係数を取得し、その大きさをスペクトルとして可視化した。
これに対してフーリエ変換では、入力データから新しい関数fを取得する。これにより、フーリエ級数展開では棒グラフだったスペクトルが、フーリエ変換では連続的な線グラフとして得られる。この線グラフが関数fそのものである。
※関数fにより(x軸:周波数, y軸:スペクトル)の線グラフが描かれるイメージ

フーリエ級数展開は離散的な周波数への分解に対応し、フーリエ変換は連続的な周波数への分解に対応する。
これは、フーリエ級数展開のフーリエ係数が離散的(n=0,1,2...)で定義されているのに対して、フーリエ変換のフーリエ係数に値するもの(フーリエ変換後のf(x))は関数であるため、(特定周波数の波の強さを表す)係数が連続的に定義されるためである。

フーリエ変換後の関数を元の関数に戻す操作をフーリエ逆変換と呼ぶ。

1.10 連続スペクトル

非周期関数の周波数スペクトルは連続的に表される。

・フーリエ変換による連続スペクトルの取得

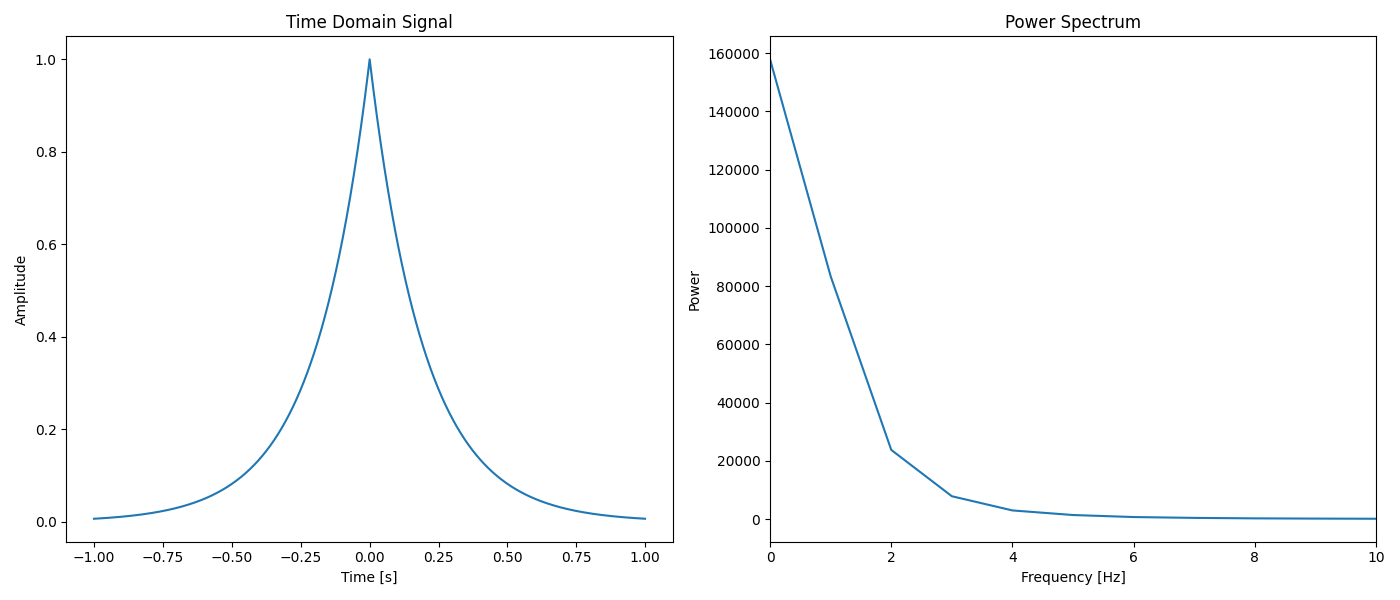
左の関数のフーリエ変換が右のグラフである。これを連続スペクトルと呼ぶ。
左の関数には、低い周波数の波の成分が含まれ、周波数が低いほど成分が強いことが分かる。

右の図は、入力波形の各周波数成分に対してフーリエ変換($\mathcal{F}(f(t))$)を行い、得られた周波数スペクトル(スカラ)をプロットした図である。
つまり、入力波形を各周波数成分に分解し、その強さ係数を求める操作がフーリエ変換であり、非周期関数では周波数成分が連続であるため、係数も連続した形状、関数(右図)として表示される。

1.11 スペクトログラム

入力波形をいくつかの窓に分割し、その窓内の波形に対してフーリエ変換を行い、得られた連続スペクトルを縦軸に色でマッピングし、時間軸に沿って各窓の連続スペクトルを縦軸に追加することで得られるデータをスペクトログラムと呼ぶ。

・スペクトログラム

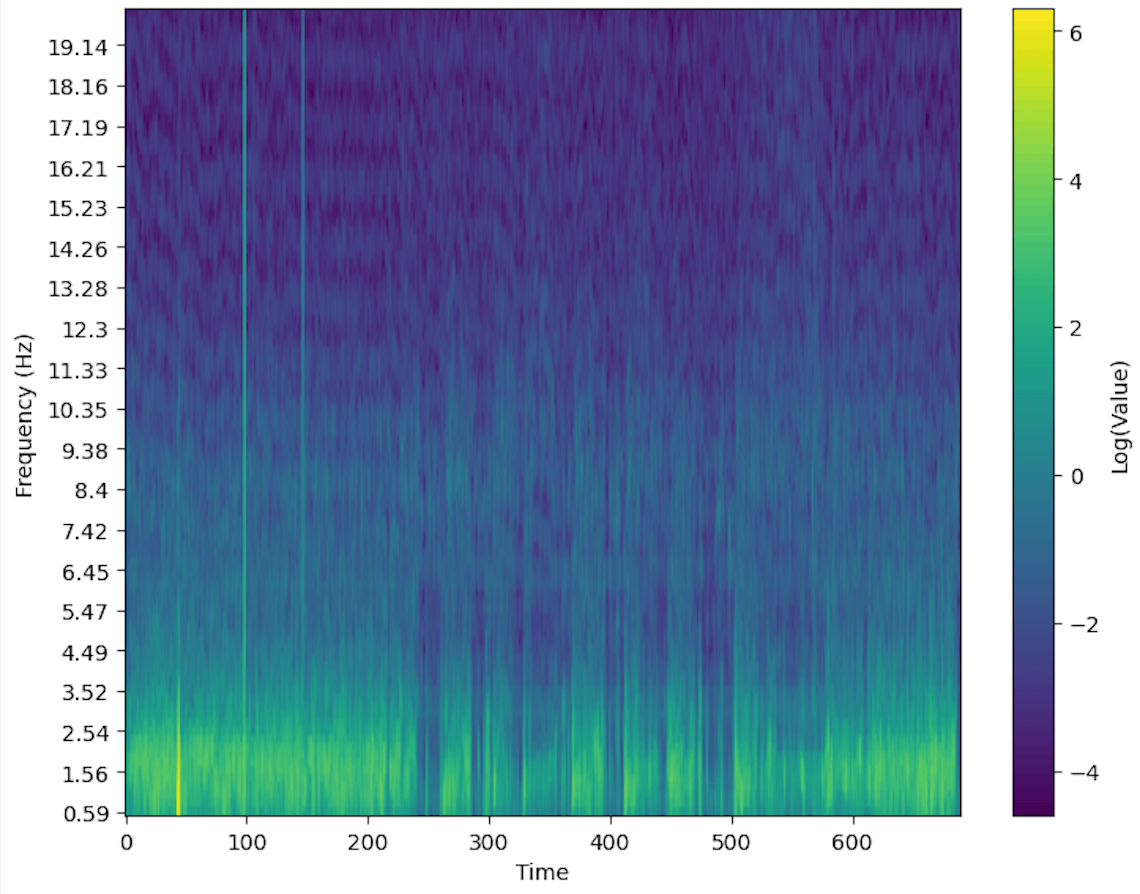
時間を区切って得られた連続スペクトルの強さを色で表現し、縦1列として左から順番に並べたものがスペクトログラムである。
この形式により、時間と周波数スペクトルを対応させて確認することができる。

音声データや脳波データの解析に利用される。

窓の大きさのトレードオフ

スペクトログラムは窓の大きさによって時間分解能と周波数分解能のトレードオフが発生する。


短い窓: 時間分解能が高まるが、周波数分解能が低下する。短期間の信号の変化を捉える必要がある場合に適している。
長い窓: 周波数分解能が高まるが、時間分解能が低下する。信号の周波数成分を詳細に分析する必要がある場合に適している。


実際には実験を重ねながら最適な窓間隔を探す必要がある。

まとめ

今回はフーリエ変換について、フーリエ級数展開から確認した。