【統計検定準1級】幾何分布

はじめに

この記事では、統計検定準1級取得に向けて学習したことをまとめていきます。
工学系の数学ではなく数理あるあるの、論述ゴリゴリな解答になっていると思いますのであらかじめご了承ください。
注意：さらに計算過程は数学文化の『省略の美』を無視してエレファントに書いています。

【リンク紹介】
・統計検定準1級のまとめ記事一覧
・これまで書いたシリーズ記事一覧

学習書籍について

この記事では「統計学実践ワークブック」を中心に、学んだことをまとめていきます。記事を読んで本格的に勉強してみたいなと思った方は、是非ご購入を検討なさってください。

参考書籍について

統計実践ワークブックは、大量の知識項目と問題が収められている反面、計算過程や知識背景が大きく省略されているため、知識体系をきちんと学ぶ参考書として東京大学から出版されている名著「統計学入門」を使っています。
※ワークブックとしては素晴らしい質だと思いますが、どうしてもその内容量とページ数の都合上、問題のない範囲で削除されているということです。人によっては1冊で問題ない方もおられると思いますが、私には無理でした。

幾何分布

定義は何を確率変数とするかで、2パターンあります。※本質的に大きな変化はありませんが、期待値が変わってしまうので要注意です。

定義１

ベルヌーイ試行において、$\bf{はじめて成功の結果が起こるまでに、\textcolor{red}{起こった失敗の結果の数}}$を、確率変数$X$とする。このとき、$X$の確率が

$$\begin{alignat*}{2} P(X = x) &= p (1 - p)^{x} \hspace{7mm} &(x = 0, 1, 2, \cdots) \\ \end{alignat*}$$

であるとき、この確率関数$p (1 - p)^{x}$を（成功確率$p$の）幾何分布(geometric distribution)といい、$Geo(p)$と表す。

定義２

ベルヌーイ試行において、$\bf{はじめて成功の結果が起こるまでの、\textcolor{red}{行った試行回数}}$を、確率変数$X$とする。このとき、$X$の確率が

$$\begin{alignat*}{2} P(X = x) &= p (1 - p)^{x - 1} \hspace{5mm} &(x = 1, 2, 3, \cdots)) \end{alignat*}$$

であるとき、この確率関数$p (1 - p)^{x - 1}$を（成功確率$p$の）幾何分布といい、$Geo(p)$と表す。
※つまりは成功結果の試行回数1回分を含んでいるため、失敗回数を表現するためにはその1回分を引いてあげないとダメということです。

確率密度関数=確率分布=分布
　統計学は数学の中でも特に、同じ意味なのにいろんな名前を持つものが多いですが、「分布」という言葉はこれまた非常に厄介です。
　結論から言うと、「分布」は「確率関数または確率密度関数」のことを指しています。多くの参考書籍の中では、なぜか同じ文章上で同時に出現する場合も多々ありますが、同じ意味です。※おそらく分布の定義の方が微妙に定義の幅が広いのですが、明らかに同義な使い方をしている場合がほとんどです。
　また、「○○分布」といわれるものはある特定の形の式の確率関数に対して付けられる名称であり、大雑把に言うと確率関数もしくは確率密度関数であることには変わりはありません。様々な分布の定義文を確認してみると、文章が曖昧な表現で書かれており、意味を正確に捉えづらいものが多いですが、意識してみると良いかもしれません。

グラフの描画

定義2のグラフ

コードはこちら

参考資料→Pythonで理解する統計解析の基礎
※参考にはしていますが表記は大分変更しています。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy.special import comb # 組み合わせ関数

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：Ge(p)
機　能：幾何分布
引　数：成功確率p
戻り値：確率変数と確率関数（X, f）
"""""""""""""""""""""""""""""""""""""""""""""""""""

def Ge(p):
    X = np.arange(1, 30)

    def f(x):
        if x in X:
            return p * ((1 - p) ** (x - 1))
        else:
            return 0

    return X, f

p = 0.5    # 成功確率
Xf = Ge(p) # 確率変数とその確率関数の値

check_prob(Xf)

plot_prob(Xf)

基本関数

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

# グラフの線の種類
linestyles = ['-', '--', ':']

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：E(Xf, g = lambda x: x)
機　能：確率変数（確率変数の関数）の期待値を返す
引　数：確率変数と確率関数X(タプル)
       確率変数Xの関数g(初期値:恒等関数)
戻り値：期待値
"""""""""""""""""""""""""""""""""""""""""""""""""""

def E(Xf, g = lambda x: x):
    X = Xf[0]    # 確率変数
    f = Xf[1]    # 確率関数
    
    expection = np.sum([g(x_k) * f(x_k) for x_k in X])
    
    return expection

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：V(Xf, g = lambda x: x)
機　能：確率変数（確率変数の関数）の分散を返す
引　数：確率変数と確率関数X(タプル)
       確率変数Xの関数g(初期値:恒等関数)
戻り値：分散
"""""""""""""""""""""""""""""""""""""""""""""""""""

def V(Xf, g = lambda x: x):
    X = Xf[0]    # 確率変数
    f = Xf[1]    # 確率関数
    expection = E(Xf, g)
    
    variance = np.sum([(g(x_k) - expection)**2 * f(x_k) for x_k in X])
    
    return variance

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：check_prob(Xf)
機　能：確率変数が確率の性質を満たしているかを確認する
引　数：確率変数と確率関数(タプル)
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def check_prob(Xf):
    X = Xf[0]    # 確率変数
    f = Xf[1]    # 確率関数
    
    prob = np.array([f(x_k) for x_k in X])
    assert np.all(prob >= 0), '負の確率があります'
    
    prob_sum = np.round(np.sum(prob), 6)
    assert prob_sum == 1, f'確率の和が{prob_sum}になりました'

    print(f'期待値は{E(Xf):.4}')
    print(f'分散は{V(Xf):.4}')

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：plot_prob(Xf)
機　能：確率関数と期待値を図示する
引　数：確率変数と確率関数X(タプル)
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def plot_prob(Xf):
    X = Xf[0]    # 確率変数
    f = Xf[1]    # 確率関数
    prob = np.array([f(x_k) for x_k in X])

    fig = plt.figure(figsize = (10, 6))
    ax  = fig.add_subplot(1, 1, 1)

    # 棒グラフ
    ax.bar(X, prob, label = 'prob', color = '#006C4F')
    
    # 縦線
    ax.vlines(E(Xf), 0, 1, label = 'expection', color = '#ee7800')

    # グラフ設定
    ax.set_xticks(np.append(X, E(Xf))) # x目盛値
#   ax.set_ytickx()                    # y目盛値  
#   ax.set_xlim()                      # x軸の範囲
    ax.set_ylim(0, prob.max() * 1.2)   # y軸の範囲
#   ax.xlabel()                        # x軸ラベル
#   ax.ylabel()                        # y軸ラベル    
    ax.legend()                        # 凡例

    # 描画
    plt.show()

幾何分布の期待値

定義１

$X$：$\bf{はじめて成功の結果が起こるまでに、\textcolor{red}{起こった失敗の結果の数}}$
$E[X]$：$X$の期待値

$$\begin{alignat*}{2} E[X] &= \cfrac{1 - p}{p} \end{alignat*}$$

定義２

$X$：$\bf{はじめて成功の結果が起こるまでの、\textcolor{red}{行った試行回数}}$
$E[X]$：$X$の期待値

$$\begin{alignat*}{2} E[X] &= \cfrac{ \ \ 1 \ \ }{p} \end{alignat*}$$

---

期待値の証明

※定義2のときで証明。定義1は定義2と同様にして証明が可能。

（証明）
期待値の定義より、

$$E[X] = \sum_{i = 1}^{\infty} x_i p(x_i)$$

と表せる。ただし、$p(x_i)$は確率関数とする。
ここで、$x_1 = 1, x_2 = 2, x_3 = 3, \cdots$であることから、

$$\begin{alignat*}{2} E[X] &= \sum_{i = 1}^{\infty} x_i p(x_i) \\ &= \sum_{i = 1}^{\infty} i \ p(i) \hspace{5mm} \cdots ① \\ \end{alignat*}$$

と表せる。また、

$$\begin{alignat*}{2} p(x_i) &= p(i) \\ &= p(1 - p)^{i - 1} \hspace{5mm} \cdots ② \\ \end{alignat*}$$

であるから、①、②より

$$\begin{alignat*}{2} E[X] &= \sum_{i = 1}^{\infty} i \ p(i) \\ &= \sum_{i = 1}^{\infty} i \ p(1 - p)^{i - 1} \\ &= p \sum_{i = 1}^{\infty} i \ (1 - p)^{i - 1} \hspace{5mm} \cdots ③ \\ \end{alignat*}$$

となる。ここで、マクローリン展開より

$$\cfrac{1}{1 - a} = 1 + a + a^2 + \cdots$$

等式の導出

マクローリン展開

$$f(x) = f(0) + f^{(1)} (0) (x - 0) + \cdots + \cfrac{f^{(n)} (0)}{n !} (x - 0)^n + \cdots$$

において、$f(x) = \cfrac{1}{1 - x}$とすると、

$$\begin{alignat*}{2} f^{(1)} (x) &= -1 \cdot (1 - x)^\prime \cdot (1 - x)^{-1 - 1} \\ &= -1 \cdot (-1) \cdot (1 - x)^{-2} \\ &= \cfrac{1}{(1 - x)^2} \\ & \\ f^{(2)} (x) &= -2 \cdot (-1) \cdot (1 - x)^{-3} \\ &= \cfrac{2}{(1 - x)^3} \\ &= (1 \cdot 2) \cfrac{1}{(1 - x)^3} & \\ f^{(3)} (x) &= 2 \cfrac{3}{(1 - x)^4} \\ &= (1 \cdot 2 \cdot 3) \cfrac{1}{(1 - x)^4} \end{alignat*}$$

であることから、

$$f^{(n)} (x) = n! \cfrac{1}{(1 - x)^{n + 1}}$$

と推測できる。※数学的帰納法で証明する必要あり
よって、

$$f^{(n)} (0) = n!$$

が成り立ち、従ってこれとマクローリン展開より

$$\begin{alignat*}{2} f(x) &= f(0) + f^{(1)} (0) (x - 0) + \cdots + \cfrac{f^{(n)} (0)}{n!} (x - 0)^n + \cdots \\ \cfrac{1}{1 - x} &= 1 + 1 \cdot x + \cdots + \cfrac{n!}{n!} \cdot x^n + \cdots \\ \cfrac{1}{1 - x} &= 1 + x + \cdots + x^n + \cdots \end{alignat*}$$

が成り立つ。

【参考にしたサイト】
https://manabitimes.jp/math/1399

が成り立つ。これを両辺$a$で微分をすると、

$$\begin{alignat*}{2} \cfrac{d}{da} \cfrac{1}{1 - a} &= \cfrac{d}{da} \left( 1 + a + a^2 + \cdots \right) \\ \cfrac{1}{(1 - a)^2} &= \sum_{k = 1}^{\infty} k a^{k - 1} \\ \end{alignat*}$$

となる。ここで、$a = 1 - p, k = i$をそれぞれ代入すると

$$\cfrac{1}{(1 - (1 - p))^2} = \sum_{i = 1}^{\infty} i \ (1 - p)^{i - 1} \hspace{5mm} \cdots ④ \\$$

となる。よって、③に④を代入すると、

$$\begin{alignat*}{2} E[X] &= p \sum_{i = 1}^{\infty} i \ (1 - p)^{i - 1} \\ &= p \times \cfrac{1}{(1 - (1 - p))^2} \\ &= p \times \cfrac{1}{p^2} \\ &= \cfrac{1}{p} \end{alignat*}$$(証明終)

【参考にしたサイト】
https://avilen.co.jp/personal/knowledge-article/geometric-distribution/

幾何分布の分散

$V[X]$：$X$の分散
※分散は定義１、定義２共通となります。

$$V[X] = \cfrac{1 - p}{p^2}$$

---

分散の証明

(証明)
分散を期待値で表すと以下のようになる。

$$V[X] = E[X^2] - (E[X])^2$$

$E[X]$は明らかであるので、$E[X^2]$を求める。期待値の定義と、$x_i$の取りうる値により

$$\begin{alignat*}{2} E[X^2] &= \sum_{i = 1}^{\infty} {x_i}^2 p(x_i) \\ &= \sum_{i = 1}^{\infty} i^2 \ p(i) \\ &= \sum_{i = 1}^{\infty} i^2 \ p (1 - p)^{i - 1} \\ &= p \sum_{i = 1}^{\infty} i^2 \ (1 - p)^{i - 1} \end{alignat*}$$

となる。ただし、$p(x_i)$は確率関数とする。ここで、

$$p \sum_{i = 1}^{\infty} i^2 \ (1 - p)^{i - 1} = \sum_{i = 1}^{\infty} (2i - 1) (1 - p)^{i - 1}$$

等式の導出

$$S_n = \sum_{i = 1}^{n} i^2 \ (1 - p)^{i - 1} \hspace{5mm} \cdots (ⅰ)$$

とおく。また、両辺に$1 - p$をかけると

$$(1 - p)S_n = \sum_{i = 1}^{n} i^2 \ (1 - p)^{i} \hspace{5mm} \cdots (ⅱ)$$

となる。よって$(ⅰ) - (ⅱ)$より

$$\begin{alignat*}{2} S_n - (1 - p)X_n &= \sum_{i = 1}^{n} i^2 \ (1 - p)^{i - 1} - \sum_{i = 1}^{n} i^2 \ (1 - p)^{i} \\ p S_n &= \sum_{i = 1}^{n} (i^2 - (i - 1)^2) (1 - p)^{i - 1} - n^2 (1 - p)^n \\ &= \sum_{i = 1}^{n} (i^2 - i^2 + 2i - 1) (1 - p)^{i - 1} - n^2 (1 - p)^n \\ &= \sum_{i = 1}^{n} (2i - 1) (1 - p)^{i - 1} - n^2 (1 - p)^n \\ \end{alignat*}$$

となる。ここで、

$$\lim_{n \to \infty} n^2 (1 - p)^n = 0$$

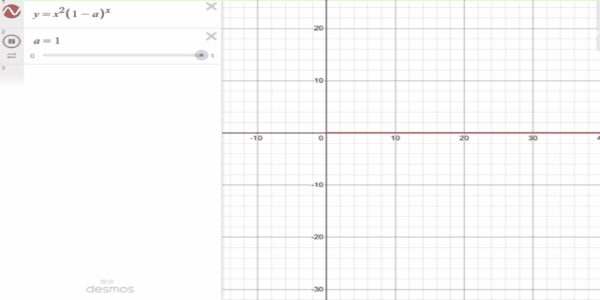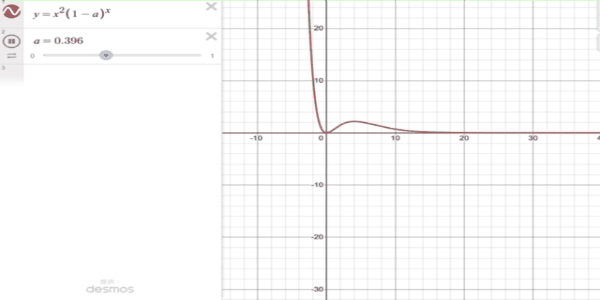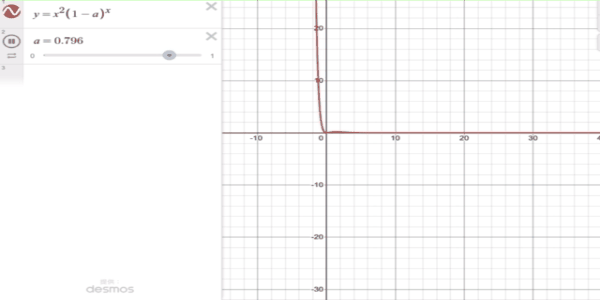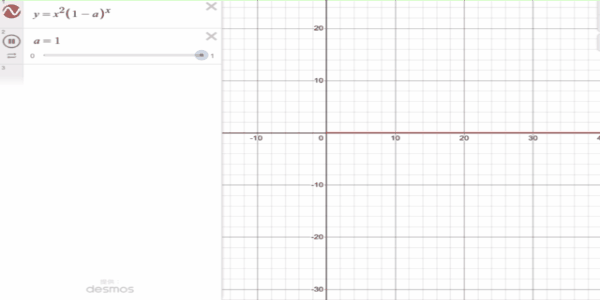
証明せずにグラフで描いてみました。

より、

$$\begin{alignat*}{2} \lim_{n \to \infty} p S_n &= \lim_{n \to \infty} \left( \sum_{i = 1}^{n} (2i - 1) (1 - p)^{i - 1} - n^2 (1 - p)^n \right) \\ &= \lim_{n \to \infty} \sum_{i = 1}^{n} (2i - 1) (1 - p)^{i - 1} \\ &= \sum_{i = 1}^{\infty} (2i - 1) (1 - p)^{i - 1} \\ \end{alignat*}$$

が成り立つので、

$$\begin{alignat*}{2} E[X^2] &= p \sum_{i = 1}^{\infty} i^2 \ (1 - p)^{i - 1} \\ &= \sum_{i = 1}^{\infty} (2i - 1) (1 - p)^{i - 1} \\ &= \sum_{i = 1}^{\infty} 2i (1 - p)^{i - 1} - \sum_{i = 1}^{\infty} (1 - p)^{i - 1} \\ &= 2 \sum_{i = 1}^{\infty} i (1 - p)^{i - 1} - \sum_{i = 1}^{\infty} (1 - p)^{i - 1} \hspace{5mm} \cdots ⑤ \\ \end{alignat*}$$

となる。ここで、$\displaystyle\sum_{i = 1}^{\infty} i (1 - p)^{i - 1}$について、初項$1$、公比$1-p$の無限等比級数であり、

$$0 < 1 - p < 1$$

より、この無限等比級数は収束し、

$$\sum_{i = 1}^{\infty} i (1 - p)^{i - 1} = \cfrac{1}{1 - (1 - p)} \hspace{5mm} \cdots ⑥$$

である。以上、⑤と④（期待値の証明）、⑥より

$$\begin{alignat*}{2} E[X^2] &= 2 \cdot \cfrac{1}{p^2} - \cfrac{1}{1 - (1 - p)} \\ &= \cfrac{2}{p^2} - \cfrac{1}{p} \end{alignat*}$$

である。したがって

$$\begin{alignat*}{2} V[X] &= E[X^2] - (E[X])^2 \\ &= \left( \cfrac{2}{p^2} - \cfrac{1}{p} \right) - \cfrac{1}{p^2} \\ &= \cfrac{1}{p^2} - \cfrac{1}{p} \\ &= \cfrac{1 - p}{p^2} \end{alignat*}$$(証明終)

【参考にしたサイト】
https://mathlandscape.com/geometric-distrib-ev/#toc6

幾何分布の確率母関数

$G(s) = E[s^X]$：$X$の確率母関数

$$\begin{alignat*}{2} G(s) &= E[s^X] \\ &= \cfrac{p}{1 - (1 - p)s}, \hspace{5mm} |s| < \cfrac{1}{1 - p} \end{alignat*}$$

例題

(「統計学実践ワークブック」より)
問5.5
あるお菓子を買うと、４種類のアニメキャラクターのカードのうちの１つが等確率でおまけとして付いてくる。
[1] 無作為復元抽出を仮定できるとき、４種類すべてのカードを揃えるまでに必要な購入回数の期待値を求めよ。
[2] ４種類のカードをすべて集めた後、お菓子を買うのをやめていたが、新しい種類のカード１枚が追加されたため再び購入をはじめた。この場合に、はじめの４種類と追加の１種類の、５種類すべてをそろえるのに必要な購入回数の期待値を$x$とする。一方、はじめから５種類が発売されていた場合に、５種類すべてを揃えるまでに必要な購入回数の期待値を$y$とする。購入回数の期待値の差$x - y$の値を求めよ。ただし、いずれの購入時期においても等確率の無作為復元抽出を仮定してよい。

解答

[1] 今、$n$種類中すでに$k \ (0 \leqq k \leqq n - 1)$種類のカードが揃っているとする。このときお菓子を買って$k + 1$種類目のカードが出る確率$p_k$は

$$p_k = \cfrac{n - k}{n} \hspace{5mm} \cdots ①$$

と表せる。ここで
「$k$種類目のカードが揃った後、$k + 1$種類目のカードが出るまでに必要な購入回数」を$x$とすると、
「$k$種類目のカードが揃った後、$k + 1$種類目のカードが$x$回目の購入で出る」確率は、

$$p_k (1 - p_k)^{x - 1}$$

である（$\bf{\textcolor{red}{定義２}}$）。つまり、この$x$を確率変数$X_k$とすると、$X_k$は(成功確率$p_k$の)幾何分布である（つまり$Geo(p_k)$）。

よって、この期待値$E[X_k]$は、

$$\begin{alignat*}{2} E[X_k] &= \cfrac{1}{p_k} \\ &= \cfrac{n}{n - k} \hspace{5mm} \cdots ② \end{alignat*}$$

である。したがって、「$n$種類すべてのカードを揃えるまでに必要な購入回数の期待値」は

$$\begin{alignat*}{2} E \left[ \sum_{k = 0}^{n - 1} X_k \right] &= \sum_{k = 0}^{n - 1} E[X_k] \\ &= \sum_{k = 0}^{n - 1} \cfrac{n}{n - k} \hspace{5mm} \cdots ③ \\ \end{alignat*}$$

と表せる。ここで、題意より$n = 4$であるから、

$$\begin{alignat*}{2} E \left[ \sum_{k = 0}^{3} X_k \right] &= \sum_{k = 0}^{3} E[X_k] \\ &= \sum_{k = 0}^{3} \cfrac{4}{4 - k} \\ &= \cfrac{4}{4} + \cfrac{4}{3} + \cfrac{4}{2} + \cfrac{4}{1} \\ &= \cfrac{4}{4} + \cfrac{4}{3} + \cfrac{4}{2} + \cfrac{4}{1} \\ &= 4 \cdot \cfrac{ 3 \cdot 2 \cdot 1 + 4 \cdot 2 \cdot 1 + 4 \cdot 3 \cdot 1 + 4 \cdot 3 \cdot 2 } {4 \cdot 3 \cdot 2 \cdot 1} \\ &= \cfrac{3 + 4 + 6 + 12}{3} \\ &= \underline{\cfrac{ \ 25 \ }{3}} \\ \end{alignat*}$$

【解答を作成しての感想】
　この解答はワークブックの解答を元に私が詳細を加筆したものになります。が、おそらくこの論理展開は実際にテストとして問題が出されたときには行わないのではないかと思います（私が統計や確率論の専門家でないため、このパターンの問題があまりにも有名である場合は話が変わりますが）。
　というのも、問題の全体像をとらえるために最初は具体的な事象、例えば「0種類目から最初の1種類目が出る確率」から観察を行うのではないか、と思うのです。（※勿論経験値が豊富な方、もしくは聡明な方は即全体像を理解できると思いますが。）そうなると、今回はたかだか4種類しかないため上式のように$n$とおいて一般化をせずとも、そのまま各期待値を出すに至るかもしれません。
　ただ、さすがに種類の値$n$がもっと大きい場合は一般化を検討するのは必須になりますし、後学のために一般化を検討することは大切なことですので、積極的に行う姿勢は大切だと思います。

かつて私も問題の作成をしていましたが、問題を作成するとき、作成者はある種の「テーマ」に注目して作成することがあります。例えば、「あ、この有名な定理を元に問題を作ってみよう！」とか、「こういうふうな解答の展開は面白そうだな！」とか、その問題の核になるようなものを先に決めて（見つけて）作成するスタイルです。
　ただ、これは注意しなければならないことがあります。それは、問題の全貌をすでに知っている作成者の視点と所見で解く解答者の視点とでは、見え方が全く異なるということです。解答者の視点を忘れて作成してしまうと、意図した解答とは程遠い解答が乱立する結果になりかねません。多彩な解答が出るならまだましですが、最悪のケースは想定していた難易度と大きく差が出たり、解釈が複数存在してしまう等の場合です。問題作成は常に、解答者の視点が必要不可欠です（過去の古傷が開きそうなのでここまでにします 涙）。

---

[2] まず期待値$x$について考える。
「4種類のカードが揃っているとき、5種類目のカードが出る確率は、[1]の①より

$$\begin{alignat*}{2} p_4 &= \cfrac{5 - 4}{5} \\ &= \cfrac{1}{5} \end{alignat*}$$

である。よってこの時の期待値は、[1]の②より

$$\begin{alignat*}{2} E[X_4] &= \cfrac{5}{5 - 4} \\ &= 5 \hspace{5mm} \cdots ④ \end{alignat*}$$

である。したがって、期待値$x$は、[1]で求めた値に④を足せばよいので、

$$\begin{alignat*}{2} x &= E \left[ \sum_{k = 0}^{3} X_k \right] + E[X_4] \\ &= \cfrac{25}{3} + 5 \\ &= \cfrac{ \ 40 \ }{3} \end{alignat*}$$

次に期待値$y$について考える。これは[1]の③の式において、$n = 5$を適用すれば求めることができる。よって、

$$\begin{alignat*}{2} y &= E \left[ \sum_{k = 0}^{4} X_k \right] \\ &= \sum_{k = 0}^{4} \cfrac{5}{5 - k} \\ &= \cfrac{5}{5} + \cfrac{5}{4} + \cfrac{5}{3} + \cfrac{5}{2} + \cfrac{5}{1} \\ & (計算過程省略) \\ &= \cfrac{137}{12} \end{alignat*}$$

以上より、

$$\begin{alignat*}{2} x - y &= \cfrac{ \ 40 \ }{3} - \cfrac{137}{12} \\ &= \cfrac{160 - 137}{12} \\ &= \underline{\cfrac{ \ 23 \ }{12}} \\ \end{alignat*}$$

参考資料

• 日本統計学会(編集).日本統計学会認定 統計検定準１級対応 統計学実践ワークブック.学術図書出版社.2020
• 東京大学教養学部統計学教室.統計学入門(基礎統計学Ⅰ).東京大学出版会.1991
• 小寺 平治.新統計入門.裳華房.1996
• 稲垣 宣生, 山根 芳知, 吉田 光雄.統計学入門.裳華房.1992
• 長瀬道弘・芦野隆一.微分積分概説.サイエンス社.2007
• 加藤文元.チャート式シリーズ 大学教養 微分積分.数研出版.2024

$\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}$
ご協力のほどよろしくお願いします。