【Python】ロジスティック回帰を使ってクラスの確率を予測するモデルの構築Part2

はじめに

この記事は株式会社インプレスの「Python機械学習プログラミング Pytorch&scilit-learn編」を読んで、私が学習したことをまとめています。
今回は3章3節の「ロジスティック回帰を使ってクラスの確率を予測するモデルの構築」を読んで学んだことをまとめていきます。
※まとめている中で、思った以上にボリュームがあったので、細かく記事を分けています。今回は「3.3.2　ロジスティック損失関数を使ってモデルの重みを学習する」を読んで学んだことをまとめています。

Part1の「3.3.1　ロジスティック回帰と条件付き確率」をまとめた記事こちらからどうぞ。

【リンク紹介】
・【一覧】Python機械学習プログラミング Pytorch&scilit-learn編
・これまで書いたシリーズ記事一覧

前回はロジスティック回帰アルゴリズムにおいて、活性化関数として与えられるシグモイド関数$\sigma_3$と、シグモイド関数をふまえた閾値関数の再定義を行いました。

今回はADALINEのときと同様に、モデルのパラメータを学習させるための損失関数$L_2$として対数尤度(ゆうど)関数(log-likelihood function)を定義します（※正確には$L_2$とは、この対数尤度関数にマイナスをつけたもののことを指します）。ADALINEの平均二乗誤差による損失関数$L_1$と明確に区別するために添え字を使って決定関数$\sigma$と同様に定義します。

定義

基本的な希望の定義は【Python】ADALINE(フルバッチ勾配降下法)と学習の収束を参考にしてください。

$\boldsymbol{w}$：重み
$b$：バイアスユニット
$\boldsymbol{x}^{(j)}$：ある特徴量の$j$番目の変数($1 \leq j \leq n$, $n$:自然数)
$y^{(j)}$：$\boldsymbol{x}^{(j)}$に対応する正解値

対数尤度関数

$\boldsymbol{x}^{(j)}$が与えられたときの正解値が$y^{(j)}$となる条件付き確率は$p(y^{(j)} | x^{(j)}, \boldsymbol{w}, b)$と表せます。

ここで、各$j$に対する条件付き確率は互いに独立であると仮定し、各条件下において$y^{(1)}, y^{(2)}, \cdots, y^{(j)}, \cdots, y^{(n)}$が同時に起こる確率は

$$\begin{alignat*}{2} & p((y^{(1)}, y^{(2)}, \cdots, y^{(j)}, \cdots, y^{(n)}) | (\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \cdots, \boldsymbol{x}^{(j)}, \cdots, \boldsymbol{x}^{(n)} ); \boldsymbol{w},b ) \\ =& p(y^{(1)} | \boldsymbol{x}^{(1)}; \boldsymbol{w},b) \times p(y^{(2)} | \boldsymbol{x}^{(2)}; \boldsymbol{w},b) \times \cdots \times p(y^{(n)} | \boldsymbol{x}^{(n)}; \boldsymbol{w},b) \\ =& \prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b) \end{alignat*}$$

です。ここで、$p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b)$について、

$$y^{(j)} \in \{ 0, 1 \}$$

であり、また【Python】ロジスティック回帰を使ってクラスの確率を予測するモデルの構築Part1より

$$p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b) = \begin{cases} \sigma_{3} (z^{(j)}) & (y^{(j)} = 1) \\ 1 - \sigma_{3} (z^{(j)}) & (y^{(j)} = 0) \\ \end{cases}$$

と表すことができます。このとき定義より$0 \leq \sigma_{3} (z^{(j)}) \leq 1$は明らかです。
以上のことから、$y^{(j)}$はベルヌーイ分布に従うため

$$p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b) = (\sigma_{3} (z^{(j)}))^{y^{(j)}} (1 - \sigma_{3} (z^{(j)}))^{1 - y^{(j)}}$$

が成り立ちます。ゆえに

$$\begin{alignat*}{2} \prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b) &= \prod_{j}^{n} (\sigma_{3} (z^{(j)}))^{y^{(j)}} (1 - \sigma_{3} (z^{(j)}))^{1 - y^{(j)}} \end{alignat*}$$

が成り立ちます。

ここで、$\displaystyle\prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b)$の対数を取ったものを対数尤度関数といいます。

$$\log \prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b)$$

損失関数$L_2$

対数尤度関数にマイナスを付与した式

$$- \log \prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b)$$

を損失関数$L_2$とします。

損失関数の定義は以上になりますが、上の形のままだと扱いづらいので以下のように式変形を行います。

$$\begin{alignat*}{2} L_2 (\boldsymbol{w}, b) &= - \log \prod_{j}^{n} p(y^{(j)} | \boldsymbol{x}^{(j)}; \boldsymbol{w},b) \\ &= - \log \prod_{j}^{n} (\sigma_{3} (z^{(j)}))^{y^{(j)}} (1 - \sigma_{3} (z^{(j)}))^{1 - y^{(j)}} \\ &= - \log \{ (\sigma_{3} (z^{(1)}))^{y^{(1)}} (1 - \sigma_{3} (z^{(1)}))^{1 - y^{(1)}} \times (\sigma_{3} (z^{(2)}))^{y^{(2)}} (1 - \sigma_{3} (z^{(2)}))^{1 - y^{(2)}} \times \cdots \times (\sigma_{3} (z^{(n)}))^{y^{(n)}} (1 - \sigma_{3} (z^{(n)}))^{1 - y^{(n)}} \} \\ &= - \{ \log (\sigma_{3} (z^{(1)}))^{y^{(1)}} (1 - \sigma_{3} (z^{(1)}))^{1 - y^{(1)}} + \log (\sigma_{3} (z^{(2)}))^{y^{(2)}} (1 - \sigma_{3} (z^{(2)}))^{1 - y^{(2)}} + \cdots + \log (\sigma_{3} (z^{(n)}))^{y^{(n)}} (1 - \sigma_{3} (z^{(n)}))^{1 - y^{(n)}} \} \\ &= - \sum_{j = 1}^{n} \left[ \log (\sigma_{3}(z^{(j)}))^{y^{(j)}} (1 - \sigma_{3} (z^{(j)}))^{1 - y^{(j)}} \right] \\ &= - \sum_{j = 1}^{n} \left[ \log (\sigma_{3} (z^{(j)}))^{y^{(j)}} + \log (1 - \sigma_{3} (z^{(j)}))^{1 - y^{(j)}} \right] \\ &= - \sum_{j = 1}^{n} \left[ y^{(j)} \log (\sigma_{3} (z^{(j)})) + (1 - y^{(j)}) \log (1 - \sigma_{3} (z^{(j)})) \right] \\ &= \underline{ \sum_{j = 1}^{n} \left[ - y^{(j)} \log (\sigma_{3} (z^{(j)})) - (1 - y^{(j)}) \log (1 - \sigma_{3} (z^{(j)})) \right]} \\ \end{alignat*}$$

なぜ「対数」尤度関数？

尤度関数ではなく、なぜ対数を取った対数尤度関数を用いているのかといえば、やはり積の計算を和に変換してしまう対数の便利な性質が理由です。計算が圧倒的に楽になります。また、マイナスを付与する理由は、対数尤度関数は最大化することによってパラメータの最適化を行うため、他の損失関数と同様に最小化で最適化を行うために付与しています。

損失関数$L_2$のグラフの描画

最後にロジスティック回帰の損失関数の値を具体的に示すグラフを描画していきます。

import

import matplotlib.pyplot as plt
import numpy as np

関数の定義

# シグモイド関数を定義
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

# y = 1 の損失値を計算する関数
def loss_1(z):
    return - np.log(sigmoid(z))

# y = 0 の損失値を計算する関数
def loss_0(z):
    return - np.log(1 - sigmoid(z))

関数の実装

# 0.1間隔で-10以上10未満のデータを生成
z = np.arange(-10, 10, 0.1)

sigma_z = sigmoid(z)                # シグモイド関数をインスタンス化
c1      = [loss_1(x) for x in z]    # y = 1の損失値を計算する関数をインスタンス化
c0      = [loss_0(x) for x in z]    # y = 0の損失値を計算する関数をインスタンス化

グラフの描画

# 結果をプロット
plt.plot(sigma_z, c1, 
         label     = 'L(w, b) if y = 1')
plt.plot(sigma_z, c0, 
         label     = 'L(w, b) if y = 0', 
         linestyle = '--')

plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\sigma(z)$')
plt.ylabel('$L_2(w, b)$')
plt.legend(loc = 'best')

# グラフを保存
plt.savefig('3-4.png')

plt.show()

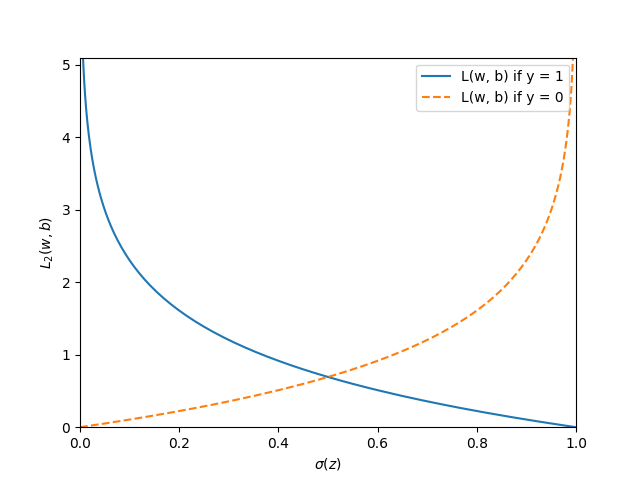
グラフを読み解く

このグラフは次のように読むことができます。

• クラス１であると正しく予測できた場合
  $\sigma_3 (z)$の値が高い(=クラス１である確率が高い)ほど、損失関数の値も0に近づく。

• クラス０であると正しく予測できた場合
  $\sigma_3 (z)$の値が低い(=クラス０である確率が高い)ほど、損失関数の値も0に近づく。

これまでの議論の流れを追えており、かつグラフの読み取りが難なくできる人ならば自明ですが、慣れていない人はそれぞれ個の情報をつなぎ合わせることは意外と難しいものです。参考に【Python】ロジスティック回帰を使ってクラスの確率を予測するモデルの構築Part1の際に描画したシグモイド関数も下図のとおり掲載しておきますので、損失関数との関係を整理するのに役立ててください。

参考文献

• Sebastian Raschka, Yuxi(Hayden)Liu, Vahid Mirjalili.Python機械学習プログラミング PyTorch&scilit-learn編.株式会社インプレス,2022
• Christopher M. Bishop.パターン認識と機械学習 上.丸善出版,2014
• Soledad Galli.データサイエンティストのための特徴量エンジニアリング.株式会社マイナビ,2023
• 寺田学, 辻真吾, 鈴木たかのり, 福島真太郎.Pythonによる新しいデータ分析の教科書 第２版.翔泳社,2023
• 三宅敏恒.線形代数学-初歩からジョルダン標準形へ-.培風館,2009
• 稲垣宣生,山根芳知,吉田光雄.統計学入門.裳華房, 2009
• 宮腰忠.高校数学+α 基礎と論理の物語.共立出版, 2013
• ベルヌーイ分布 by WIIS
• ベルヌーイ分布とは～定義と性質の導出～ by 数学の景色

$\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}$
ご協力のほどよろしくお願いします。