【Python】ロジスティック回帰を使ってクラスの確率を予測するモデルの構築Part1

はじめに

この記事は株式会社インプレスの「Python機械学習プログラミング Pytorch&scilit-learn編」を読んで、私が学習したことをまとめています。
今回は3章3節の「ロジスティック回帰を使ってクラスの確立を予測するモデルの構築」を読んで学んだことをまとめていきます。
※まとめている中で、思った以上にボリュームがあったので、細かく記事を分けています。今回は「3.3.1　ロジスティック回帰と条件付き確率」を読んで学んだことをまとめています。
また、用語などの定義については【Python】ADALINE(フルバッチ勾配降下法)と学習の収束にまとめていますので、こちらをご確認ください。

【リンク紹介】
・【一覧】Python機械学習プログラミング Pytorch&scilit-learn編
・これまで書いたシリーズ記事一覧

ロジット関数

ロジット関数の定義

ロジスティック回帰(logostic regression)とは、ADALINEの活性化関数を恒等関数ではなくシグモイド関数(sigmoid function)

$$\sigma_{3}^{(z)} = \cfrac{1}{1 + e^{-z}}$$

に置き換えたものです。よって、ここではシグモイド関数についてお話します。

まず、事象(event)とは結果として起こる事柄のことを言い、正事象(positive event)とは予測したい事象であるとします。そして正事象の確立を$p$で表します。またこの確率$p$は、特徴量$\boldsymbol{x}$が与えられているときに、クラスラベル(正解値)が$y$となる事象の条件付き確率として定義できます。つまり

$$p := p(y|\boldsymbol{x})$$

と書くことができます。（※この記事で用いられている$y$や$z$などの値は、【Python】ADALINE(フルバッチ勾配降下法)と学習の収束の時とは違い、インデックスによる順位付けを考慮しておらず、一般化して話をしていますのでご注意下さい。）
ここで、比$\cfrac{p}{1 - p}$をオッズ比といいます。

このオッズ比の対数をとって確率$p$を変数$(ただし0 < p < 1)$とみなして関数ととらえることとし、ロジット関数(logit function)と定め、

$$\begin{alignat*}{2} \text{logit}(p) &= \log_{e} \cfrac{p}{1 - p} \end{alignat*}$$

と表すこととします。

ロジット関数のグラフ

すると、ロジット関数は次のようなグラフになります。

import

!pip install japanize_matplotlib > /dev/null    # matplotlibで日本語表示を行う

import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib

# 0から1まで50個の配列を作る
x = np.linspace(0, 1, 50)

# ロジット関数を定義
y = np.log (x / (1 - x))

# 結果を描画
plt.plot(x, y, color = '#3F9877')

# 縦軸を追加
ymin, ymax = -4, 4
plt.vlines(0.5, ymin, ymax, color = 'black')

# 横線を追加
xmin, xmax = 0, 1
plt.hlines(0, xmin, xmax, color = 'black')

plt.xlabel('p')
plt.ylabel('logit(p)')

# グラフを保存
plt.savefig('logit_function.png')

plt.grid()
plt.show()

ロジット関数を定義

# 0から1まで50個の配列を作る
x = np.linspace(0, 1, 50)

# ロジット関数を定義
y = np.log (x / (1 - x))

ロジット関数を描画

# 結果を描画
plt.plot(x, y, color = '#3F9877')

# 縦軸を追加
ymin, ymax = -4, 4
plt.vlines(0.5, ymin, ymax, color = 'black')

# 横線を追加
xmin, xmax = 0, 1
plt.hlines(0, xmin, xmax, color = 'black')

plt.xlabel('p')
plt.ylabel('logit(p)')

# グラフを保存
plt.savefig('logit_function.png')

plt.grid()
plt.show()

[参考資料]

• [Python] 対数関数グラフの書き方 by雪菜さん
• 【Python】Matplotlibで縦線・横線を描く方法を紹介！

公理論的確率

先ほどのロジット関数の$p$の定義域について、$0 < p < 1$といいましたが、確率の定義を理解している人からすると、おかしくないか？と思われる方がいるかもしれません。

そもそも数学における確率の定義とは、1933年にコルモゴロフが定義した公理論的定義にもとづくものであり、その定義は以下の通りです。

---

$S$を標本空間とし、$A$をそれに属する部分集合(事象)とする。$P(・)$が次の3つの条件を満たすとき、この$P$を標本空間$S$の集合に対して定義された確率速度といい、$P(A)$を事象Aの確率という。

1. $P(A) \geq 0$
2. $P(S) = 1$
3. $A_1, A_2, \cdots, A_n$が$S$内の互いに排反な事象$( i \neq j$なる$i, j$について、$A_i \cap A_j = \emptyset)$のとき、
   

$$P(A_1 \cup A_2 \cup \cdots \cup A_n) = P(A_1) + P(A_2) + \cdots + P(A_n)$$(「統計学入門」.稲垣宣生.山根芳知.吉田光雄.2009)

---

よって、確率であるならば0と1を定義域に含むべきなのですが、真数の$\cfrac{p}{1 - p}$において、$p = 1$のとき、分数の定義により式が成立せず、$p = 0$のとき、今度は対数の定義より式が成立しないため、除外しなければなりません。これに関する記述は省かれている場合が非常に多く、もしかすると困る部分かもしれないと思い追記しました。また、値域についてはグラフを見ても明らかですが、

$$\lim_{x \to 0} \log \cfrac{p}{1 - p} = - \infty \\ \lim_{x \to 1} \log \cfrac{p}{1 - p} = \infty$$

より、$(- \infty, \infty)$です。

シグモイド関数

シグモイド関数の定義

さて、このロジット関数ですが、ロジスティックモデルにおいては総入力$z = \boldsymbol{w}^{T} \boldsymbol{x} + b$と等しいものであると仮定します。つまり次の式が成り立つと仮定します。

$$\begin{alignat*}{2} \text{logt}(p) &= \boldsymbol{w}^{T} \boldsymbol{x} + b \\ &= z \end{alignat*}$$

この関数の逆関数が、冒頭で出てきたシグモイド関数となります。導出は以下の通りです。

$$\begin{alignat*}{2} \text{logit} (p) &= z \\ \log_e \cfrac{p}{1 - p} &= z \\ \cfrac{p}{1 - p} &= e^{z} \\ \cfrac{p}{1 - p} &= - e^{z} \\ \cfrac{p}{p - 1} &= - e^{z} \\ \cfrac{(p - 1) + 1}{p - 1} &= - e^{z} \\ 1 + \cfrac{1}{p - 1} &= - e^{z} \\ \cfrac{1}{p - 1} &= - 1 - e^{z} \\ p - 1 &= - \cfrac{1}{1 + e^{z}} \\ p &= 1 - \cfrac{1}{1 + e^{z}} \\ p &= \cfrac{1 + e^{z} - 1}{1 + e^{z}} \\ p &= \cfrac{e^{z}}{1 + e^{z}} \\ p &= \cfrac{e^{z} \times \cfrac{1}{e^{z}} }{(1 + e^{z}) \times \cfrac{1}{e^{z}}} \\ p &= \cfrac{1}{\cfrac{1}{e^{z}} + 1} \\ p &= \cfrac{1}{1 + e^{-z}} \\ \end{alignat*}$$

シグモイド関数のグラフ

では実際にシグモイド関数を描画してみます。

シグモイド関数を定義と実装

# シグモイド関数を定義
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

# 0.1間隔で-7以上7未満のデータを作成
z = np.arange(-7, 7, 0.1)

# シグモイド関数を実行
sigma_z = sigmoid(z)

シグモイド関数を描画

# 結果を描画
plt.plot(z, sigma_z, color = '#3F9877')

# 垂直線を追加(z = 0)
plt.axvline(0.0, color = 'k')
# y軸の上限/下限を設定
plt.ylim(-0.1, 1.1)

# 軸のラベルを設定
plt.xlabel('z')
plt.ylabel('$\sigma_3 (z)$')
# y軸のメモリを追加
plt.yticks([0.0, 0.5, 1.0])

# Axesクラスのオブジェクトの取得
ax = plt.gca()
# y軸のメモリに合わせて水平グリッド線を追加
ax.yaxis.grid(True)

# グラフを保存
plt.savefig('3-2.png')

plt.show()

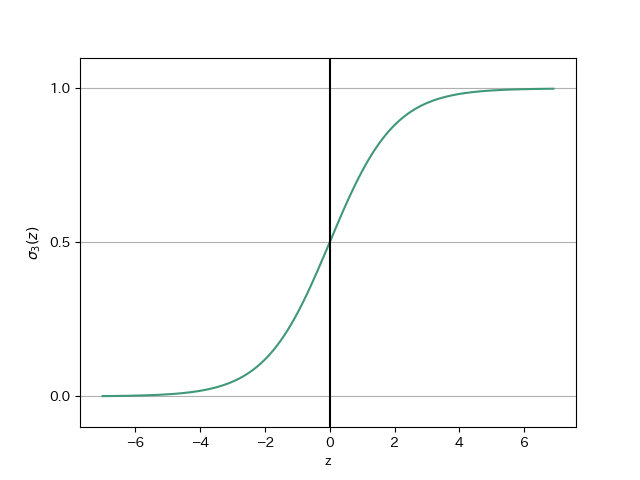
グラフより、$z$の値が大きいほどシグモイド関数は1に近づき、反対に小さい値に行くほど0に近づくことがわかります。導出で示した通りシグモイド関数は確率$p$と同じです。つまりクラスラベル(正解値)が1である確率を次のように表すことができます。

$$\begin{alignat*}{2} \sigma_3 (z) &= p \\ &= p(y | \boldsymbol{x} ; \boldsymbol{w}, b) \\ & ※重みとバイアスが与えられているとする \end{alignat*}$$

閾値関数を再定義する

したがって、シグモイド関数は入力値を受け取り、$\sigma_3 (0) = 0.5$を切片として、クラスに属する確率を表しているとして解釈することができます。
よって、閾値関数を切片が0.5であることに注目して以下のように定義すればよいです。

$$\begin{alignat*}{2} \hat{y} &= \begin{cases} 1 & \sigma_3 (z) \geq 0.5 \\ 0 & \sigma_3 (z) < 0.5 \\ \end{cases} \\ &= \begin{cases} 1 & z \geq 0 \\ 0 & z < 0 \\ \end{cases} \end{alignat*}$$

再定義とは書きましたが、結論だけ見ればこれまでの閾値関数と変わりません。

参考文献

• Sebastian Raschka, Yuxi(Hayden)Liu, Vahid Mirjalili.Python機械学習プログラミング PyTorch&scilit-learn編.株式会社インプレス,2022
• Christopher M. Bishop.パターン認識と機械学習 上.丸善出版,2014
• Soledad Galli.データサイエンティストのための特徴量エンジニアリング.株式会社マイナビ,2023
• 寺田学, 辻真吾, 鈴木たかのり, 福島真太郎.Pythonによる新しいデータ分析の教科書 第２版.翔泳社,2023
• 三宅敏恒.線形代数学-初歩からジョルダン標準形へ-.培風館,2009
• 稲垣宣生,山根芳知,吉田光雄.統計学入門.裳華房, 2009
• 宮腰忠.高校数学+α 基礎と論理の物語.共立出版, 2013

$\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}$
ご協力のほどよろしくお願いします。