【Python】ADALINE(確率的勾配降下法)と学習の収束
はじめに
この記事は株式会社インプレスの「Python機械学習プログラミング Pytorch&scilit-learn編」を読んで、私が学習したことをまとめています。
今回は2章3節のADALINEと学習の収束を読んで学んだことをまとめていきます。
また、この記事は【Python】ADLINE(フルバッチ勾配降下法)と学習の収束の続きとして書かれており、定義などは前回の記事にまとめられています。
前回はADALINEの損失関数に対してフルバッチ勾配降下法を用いて、パラメータの最適化を行いましたが、フルバッチ勾配降下法はそのアルゴリズム上、大域的極小値に1ステップ近づくごとに訓練データセット全体を評価する必要があることから、計算量が多くなることがあります。
そんなフルバッチ勾配降下法の代わりによく用いられるものに、確率的勾配降下法(stochastic gradient descent)という手法があります。この記事では前回のADALINEの改良版として、この確率的勾配降下法を用いたADALINEの実装、および学習の収束について学んだことをまとめていきます。
【リンク紹介】
・【一覧】Python機械学習プログラミング Pytorch&scilit-learn編
・これまで書いたシリーズ記事一覧
確率的勾配降下法について
確率的勾配降下法はフルバッチ勾配降下法とは異なり、重みやバイアスのパラメータ更新を訓練データごとに漸進的(ぜんしんてき)に更新します。つまり、以下のように定義をします。
式の導出のヒントは【Python】ADLINE(フルバッチ勾配降下法)と学習の収束の重さとバイアスの計算過程を参照するとイメージできると思います。計算過程については参考書よりも詳細を書いていますので、是非参考にされてください。
ライブラリのインポート
import numpy as np
import os
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
ADLINE(確率的勾配降下法)の実装
ADAptive LInear NEuron分類器を実装していきいます。
class AdalineSGD:
"""
パラメータ
----------------------------------------------------
eta : float.学習率
n_iter : int.訓練データの訓練回数
random_state : int.重みを初期化するための乱数シード
----------------------------------------------------
データ属性
----------------------------------------------------
w_ : 1次元配列.適合後の重み
b_ : スカラー.適合後のバイアス
losses_ : リスト.各エポックでの損失関数の値
----------------------------------------------------
"""
def __init__(self, eta = 0.01, n_iter = 10, shuffle = True, random_state = None):
self.eta = eta # 学習率の初期化
self.n_iter = n_iter # 訓練回数の初期化
self.random_state = random_state # 乱数シードを設定
# new
self.w_initialized = False # 重みの初期化フラグはFalse(未初期化)に設定
self.shuffle = shuffle # 各エポックで訓練データをシャッフルするかどうか
def fit(self, X, y):
"""
パラメータ
-----------------------------------------------------------------------------------------------
X : {配列のようなデータ構造}. shape = [n_examples(訓練データの個数), n_features(特徴量の個数)]
y : {配列のようなデータ構造}. shape = [n_examples(訓練データの個数)]
-----------------------------------------------------------------------------------------------
"""
self._initialize_weights(X.shape[1]) # 重みベクトルの生成
self.losses_ = [] # 損失値を格納するリストの作成
# 訓練回数分まで訓練データを反復
for i in range(self.n_iter):
# 指定された場合は訓練データをシャッフル
if self.shuffle:
X, y = self._shuffle(X, y)
# 各訓練データの損失値を格納するリストを生成
losses = []
for xi, target in zip(X, y):
# 特徴量xiと目的変数yを使った重みの更新と損失値の計算
losses.append(self._update_weights(xi, target))
# 訓練データの平均損失値の計算
avg_loss = np.mean(losses)
# 平均損失値を格納
self.losses_.append(avg_loss)
return self
# オンライン学習(online learning)
def partial_fit(self, X, y):
"""重みを再初期化することなく訓練データに適合させる"""
# 初期化されていない場合は初期化を実行
if not self.w_initialized:
self._initialize_weights(X.shape[1])
# 目的変数yの要素数が2以上の場合は各訓練データの特徴量xiと目的変数tartgetで重みを更新する
if y.rabel().shape[0] > 1:
for xi, target in zip(X,y):
self._update_weights(xi, target)
# 目的変数yの要素数が1の場合は訓練データ全体の特徴量Xと目的変数yで重みを更新
else:
self._update_weights(X, y)
return self
def _shuffle(self, X, y):
"""訓練データをシャッフル"""
r = self.rgen.permutation(len(y))
return X[r], y[r]
def _initialize_weights(self, m):
"""重みを小さな乱数で初期化"""
self.rgen = np.random.RandomState(self.random_state)
self.w_ = self.rgen.normal(loc = 0.0,
scale = 0.01,
size = m
)
self.b_ = np.float_(0.)
self.w_initialized = True # フラグをTrueに変える。つまり「初期化済」
def _update_weights(self, xi, target):
output = self.activation(self.net_input(xi)) # 活性化関数の出力を計算
error = (target - output) # 誤差を計算
self.w_ += self.eta * 2.0 * xi * (error) # 重みを更新
self.b_ += self.eta * 2.0 * error # バイアスを更新
loss = error ** 2 # 損失関数を計算
return loss
def net_input(self, X):
return np.dot(X, self.w_) + self.b_ # 総入力を算出
def activation(self, X): # 線形活性化関数の出力を計算
return X # ただの恒等関数
def predict(self, X):
return np.where(self.activation(self.net_input(X)) >= 0.5, 1, 0)
IrisデータでADLINEモデルの訓練
それでは、実装したADALINE(確率的勾配降下法)を用いて学習の収束の様子を見てみたいと思います。
まずはデータセットの準備を行います。
s = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
print('From URL:', s)
# IrisデータセットをDaraFrameオブジェクトに直接読み込む
df = pd.read_csv(s,
header = None,
encoding = 'utf-8')
df.tail()
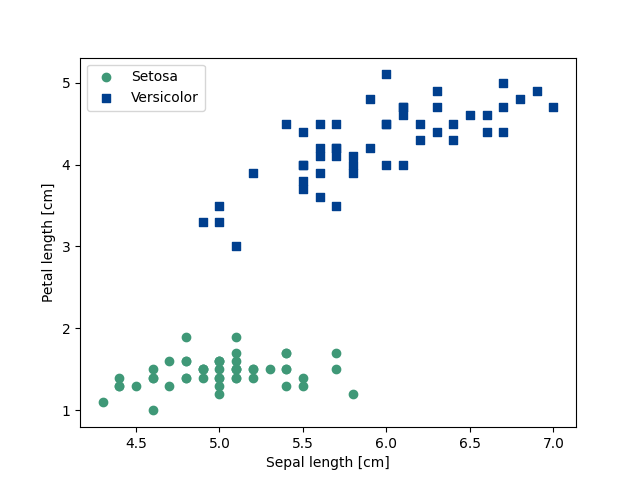
散布図を用いてデータを可視化する
がく片の長さと花びらの長さを抽出し、散布図を用いてデータを可視化していきます。
# 1-100行目の1, 3行目(がく片の長さ、花びらの長さ)の抽出 ※今回扱う特徴量は2つ
X = df.iloc[0 : 100, [0, 2]].values
# 1-100行目の目的変数の抽出
y = df.iloc[0 : 100, 4].values
# Iris-setosaを0, Iris-versicolorを1に変換
y = np.where(y == 'Iris-setosa', 0, 1)
# 品種setosaのプロット(緑の●)
plt.scatter(x = X[:50, 0],
y = X[:50, 1],
color = '#3F9877',
marker = 'o',
label = 'Setosa')
# 品種Versicolorのプロット(青の■)
plt.scatter(x = X[50 : 100, 0],
y = X[50 : 100, 1],
color = '#003F8E',
marker = 's',
label = 'Versicolor')
# 軸のラベルの設定
plt.xlabel('Sepal length [cm]')
plt.ylabel('Petal length [cm]')
# 凡例の設定
plt.legend(loc = 'upper left')
# グラフを保存
plt.savefig('fig2-6.png')
plt.show()
特徴量のスケーリング
前回のADALINE(フルバッチ勾配降下法)のときと同様に学習効率の向上のため、標準化によるスケーリングを行います。
# データのコピー
X_std = np.copy(X)
# 各列の標準化
X_std[:, 0] = (X[:, 0] - X[:, 0].mean()) / X[:, 0].std()
X_std[:, 1] = (X[:, 1] - X[:, 1].mean()) / X[:, 1].std()
決定境界を可視化する関数の実装
2次元のデータセットの決定境界を可視化するための関数を実装します。
def plot_decision_regions(X, y, classifier, test_idx = None, resolution = 0.02):
"""マーカーとカラーマップの準備"""
markers = ('o', 's', '^', 'v', '<')
colors = ('#3F9877', # ジェードグリーン
'#003F8E', # インクブルー
'#EA5506', # 赤橙
'gray',
'cyan'
)
cmap = ListedColormap(colors[: len(np.unique(y))])
"""グリッドポイント(格子点)の生成"""
# x軸方向の最小値、最大値を定義
x_min = X[:, 0].min() - 1
x_max = X[:, 0].max() + 1
# y軸方向の最小値、最大値を定義
y_min = X[:, 1].min() - 1
y_max = X[:, 1].max() + 1
# 格子点の生成
xx, yy = np.meshgrid(np.arange(x_min, x_max, resolution),
np.arange(y_min, y_max, resolution)
)
# 確認用
#print(xx1)
#print(xx2)
"""各特徴量を1次元配列に変換(ravel())して予測を実行"""
# つまり2つの特徴量から0と予測された格子点と1と予測された値が格子点ごとにlabに格納される
lab = classifier.predict(np.array([xx.ravel(), yy.ravel()]).T)
# 確認用
#print(np.array([xx1.ravel(), xx2.ravel()]).T)
#print(lab) # 格子点の並びで0,1が格納されているが、この時点では1次元配列なので変換が必要
"""予測結果の元のグリッドポイント(格子点)のデータサイズに変換"""
lab = lab.reshape(xx.shape)
"""グリッドポイントの等高線のプロット"""
plt.contourf(xx, yy, lab,
alpha = 0.3, # 透過度を指定
cmap = cmap
)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
"""決定領域のプロット"""
# クラスごとに訓練データをセット
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x = X[y == cl, 0],
y = X[y == cl, 1],
alpha = 0.8,
c = colors[idx],
marker = markers[idx],
label = f'Class {cl}',
edgecolor = 'black'
)
"""テストデータ点を目立たせる(点を〇で表示)"""
if test_idx: # ここはbool(test_idx)と同義。つまりTrueを返す
# すべてのデータ点を描画
X_test = X[test_idx, :]
y_test = y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
c = 'none',
edgecolor = 'black',
alpha = 1.0,
linewidth = 1,
marker = 'o',
s = 100,
label = 'Test set'
)
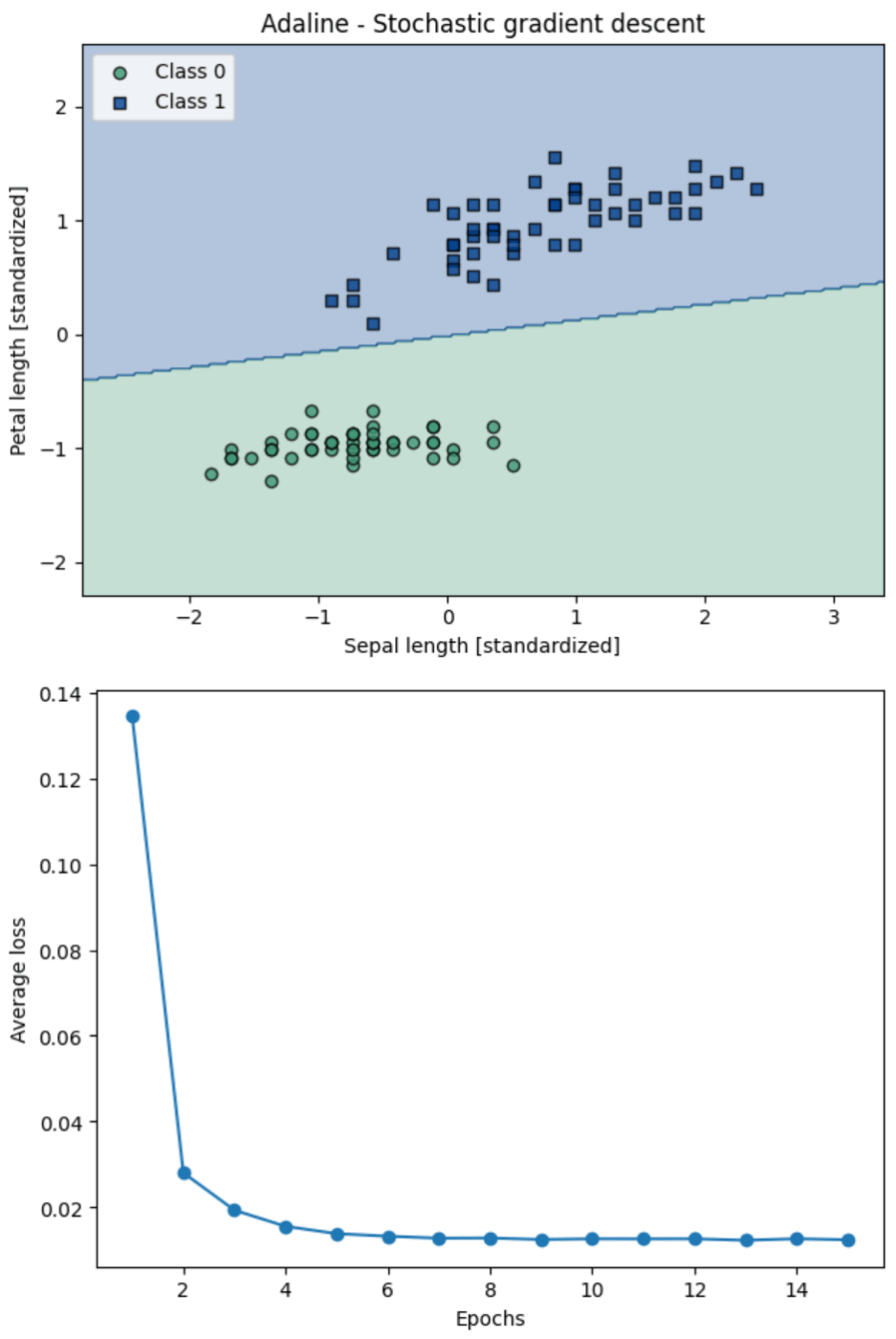
ADALINEのアルゴリズムを用いて訓練する
# 確率的勾配法によるADALINEの学習
ada_sgd = AdalineSGD(n_iter = 15, eta = 0.01, random_state = 1)
# モデルの学習
ada_sgd.fit(X_std, y)
# 決定領域のプロット
plot_decision_regions(X_std, y, classifier = ada_sgd)
plt.title('Adaline - Stochastic gradient descent')
plt.xlabel('Sepal length [standardized]')
plt.ylabel('Petal length [standardized]')
plt.legend(loc = 'upper left')
plt.tight_layout()
# グラフを保存
plt.savefig('fig2-15-1.png')
plt.show()
# エポック数と損失値の関係を表す折れ線グラフの描画
plt.plot(range(1, len(ada_sgd.losses_) + 1), ada_sgd.losses_, marker = 'o')
plt.xlabel('Epochs')
plt.ylabel('Average loss')
plt.tight_layout()
# グラフを保存
plt.savefig('fig2-15-2.png')
plt.show()
参考文献
- Sebastian Raschka, Yuxi(Hayden)Liu, Vahid Mirjalili.Python機械学習プログラミング PyTorch&scilit-learn編.株式会社インプレス,2022
- Christopher M. Bishop.パターン認識と機械学習 上.丸善出版,2014
- Soledad Galli.データサイエンティストのための特徴量エンジニアリング.株式会社マイナビ,2023
- 寺田学, 辻真吾, 鈴木たかのり, 福島真太郎.Pythonによる新しいデータ分析の教科書 第2版.翔泳社,2023
- 三宅敏恒.線形代数学-初歩からジョルダン標準形へ-.培風館,2009
ご協力のほどよろしくお願いします。

Discussion