【統計検定準1級】正規分布

はじめに

この記事では、統計検定準1級取得に向けて学習したことをまとめていきます。
工学系の数学ではなく数理あるあるの、論述ゴリゴリな解答になっていると思いますのであらかじめご了承ください。
注意：さらに計算過程は数学文化の『省略の美』を無視してエレファントに書いています。

【リンク紹介】
・統計検定準1級のまとめ記事一覧
・これまで書いたシリーズ記事一覧

学習書籍について

この記事では「統計学実践ワークブック」を中心に、学んだことをまとめていきます。記事を読んで本格的に勉強してみたいなと思った方は、是非ご購入を検討なさってください。

参考書籍について

統計実践ワークブックは、大量の知識項目と問題が収められている反面、計算過程や知識背景が大きく省略されているため、知識体系をきちんと学ぶ参考書として東京大学から出版されている名著「統計学入門」を使っています。
※ワークブックとしては素晴らしい質だと思いますが、どうしてもその内容量とページ数の都合上、問題のない範囲で削除されているということです。人によっては1冊で問題ない方もおられると思いますが、私には無理でした。

正規分布

確率変数$X$が連続型であるとする。この$X$に対し、確率密度関数$f$が

$$f(x) = \cfrac{1}{\sqrt{2 \pi} \sigma} \exp \left( - \cfrac{(x - \mu)^2}{2 \sigma^2} \right) \hspace{5mm} (- \infty < x < \infty)$$

であるとき、この確率密度関数$f$を平均$\mu$、分散$\sigma^2$の正規分布(normal distribution)といい、$N(\mu, \sigma^2)$と表す。ただし、$\mu, \sigma$は実数で$\sigma > 0$である。

確率密度関数=確率分布=分布
　統計学は数学の中でも特に、同じ意味なのにいろんな名前を持つものが多いですが、「分布」という言葉はこれまた非常に厄介です。
　結論から言うと、「分布」は「確率関数または確率密度関数」のことを指しています。多くの参考書籍の中では、なぜか同じ文章上で同時に出現する場合も多々ありますが、同じ意味です。※おそらく分布の定義の方が微妙に定義の幅が広いのですが、明らかに同義な使い方をしている場合がほとんどです。
　また、「○○分布」といわれるものはある特定の形の式の確率関数に対して付けられる名称であり、大雑把に言うと確率関数もしくは確率密度関数であることには変わりはありません。様々な分布の定義文を確認してみると、文章が曖昧な表現で書かれており、意味を正確に捉えづらいものが多いですが、意識してみると良いかもしれません。

グラフの描画

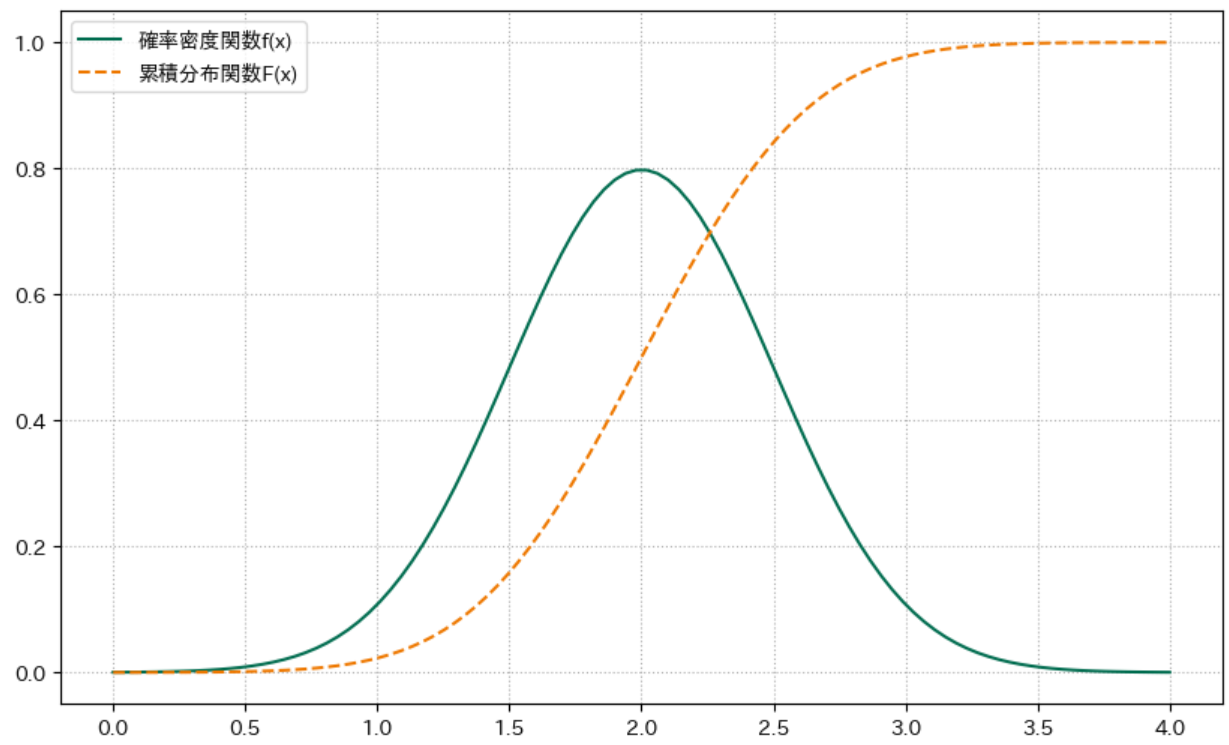
コードはこちら

参考資料→Pythonで理解する統計解析の基礎
※参考にはしていますが表記は大分変更しています。

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib                    # グラフ上での日本語表示
from scipy import stats, integrate
from scipy.optimize import minimize_scalar    # 関数の最小値を求める

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：N(mu, sigma)
機　能：正規分布
引　数：期待値mu, 標準偏差sigma
戻り値：連続型確率変数と確率密度関数（X, f）
"""""""""""""""""""""""""""""""""""""""""""""""""""

def N(mu, sigma):
    # 連続型確率変数
    X = [-np.inf, np.inf]

    # 確率密度関数
    def f(x):
        return (1 / np.sqrt(2 * np.pi * sigma**2)) * np.exp(-(x - mu)**2 / (2 * sigma**2))

    return X, f

mu    = 2      # 期待値
sigma = 0.5    # 標準偏差
Xf     = N(mu, sigma)

check_prob(Xf)

plot_prob(Xf, 0, 4)

基本関数

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib                    # グラフ上での日本語表示
from scipy import stats, integrate
from scipy.optimize import minimize_scalar    # 関数の最小値を求める

# 表示桁数を小数点以下第３位に設定
%precision 3

# [Jupyter notebook only]
# グラフ表示を非インタラクティブモード(jupyter notebook内に表示)に設定
# インタラクティブモードだと別ウィンドウで表示される
%matplotlib inline

# グラフの線の種類
linestyles = ['-', '--', ':']

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：E(Xf, g = lambda x: x)
機　能：連続型確率変数（確率変数の関数）の期待値を返す
引　数：連続型確率変数と確率関数X(タプル)
       連続型確率変数Xの関数g(初期値:恒等関数)
戻り値：期待値
"""""""""""""""""""""""""""""""""""""""""""""""""""

def E(Xf, g = lambda x: x):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数

    def integrand(x):
        return g(x) * f(x)
    
    expection = integrate.quad(func = integrand,    # 被積分関数
                               a    = -np.inf,      # 積分区間
                               b    = np.inf        # 積分区間
                              )[0]
    
    return expection

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：V(Xf, g = lambda x: x)
機　能：連続型確率変数（確率変数の関数）の分散を返す
引　数：連続型確率変数と確率関数X(タプル)
       連続型確率変数Xの関数g(初期値:恒等関数)
戻り値：分散
"""""""""""""""""""""""""""""""""""""""""""""""""""

def V(Xf, g = lambda x: x):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    expection = E(Xf, g)

    def integrand(x):
        return (g(x) - expection) ** 2 * f(x)
    
    variance = integrate.quad(func = integrand,    # 被積分関数
                              a    = -np.inf,      # 積分区間
                              b    = np.inf        # 積分区間
                             )[0]
    
    return variance

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：check_prob(Xf)
機　能：連続型確率変数が確率の性質を満たしているかを確認する
引　数：連続型確率変数と確率密度関数(タプル)
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def check_prob(Xf):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    
    f_min = minimize_scalar(f).fun
    assert f_min >= 0, '確率密度関数が負の値をとります'
    
    prob_sum = np.round(integrate.quad(f, -np.inf, np.inf)[0], 6)
    assert prob_sum == 1, f'確率の和が{prob_sum}になりました'

    print(f'期待値は{E(Xf):.3f}')
    print(f'分散は{V(Xf):.3f}')

"""""""""""""""""""""""""""""""""""""""""""""""""""
関数名：plot_prob(Xf, x_min, x_max)
機　能：確率密度関数と期待値を図示する
引　数：連続型確率変数と確率密度関数X(タプル)
       定義域の最低値
       定義域の最大値
戻り値：なし
"""""""""""""""""""""""""""""""""""""""""""""""""""

def plot_prob(Xf, x_min, x_max):
    X = Xf[0]    # 連続型確率変数
    f = Xf[1]    # 確率密度関数
    
    # 累積分布関数
    def F(x):
        return integrate.quad(f, -np.inf, x)[0]

    xs = np.linspace(x_min, x_max, 100)

    fig = plt.figure(figsize = (10, 6))
    ax  = fig.add_subplot(1, 1, 1)

    # 確率密度関数のグラフ
    ax.plot(xs, [f(x) for x in xs], label = '確率密度関数f(x)', color = '#006C4F')
    
    # 累積分布関数のグラフ
    ax.plot(xs, [F(x) for x in xs], label = '累積分布関数F(x)', ls = '--', color = '#ee7800')

    # グラフ設定
#   ax.set_xticks(np.append(X, E(Xf))) # x目盛値
#   ax.set_ytickx()                    # y目盛値  
#   ax.set_xlim()                      # x軸の範囲
#   ax.set_ylim()                      # y軸の範囲
#   ax.xlabel()                        # x軸ラベル
#   ax.ylabel()                        # y軸ラベル    
    ax.legend()                        # 凡例

    # 描画
    plt.show()

正規分布の再生性

$X_1, X_2, \cdots, X_n$が独立で、それぞれ正規分布$N(\mu_1, {\sigma_1}^2), N(\mu_2, {\sigma_2}^2), \cdots, N(\mu_n, {\sigma_n}^2)$に従うならば、以下の2つが成り立つ。

1. $X_1 + X_2 + \cdots + X_n$は$N(\mu_1 + \mu_2 + \cdots + \mu_n, {\sigma_1}^2 + {\sigma_s}^2 + \cdots + {\sigma_n}^2)$に従う。

2. $c_1 X_1 + c_2 X_2 + \cdots + c_n X_n$は$N(c_1 \mu_1 + c_2 \mu_2 + \cdots c_n \mu_n, {c_1}^2 {\sigma_1}^2 + {c_2}^2 {\sigma_2}^2 + \cdots + {c_n}^2 {\sigma_n}^2)$に従う。
   ただし、$c_1, c_2, \cdots, c_n$は定数とする。

特に$X_1, X_2, \cdots, X_n$の確率分布がすべて正規分布$N(\mu, \sigma^2)$に従うならば、以下の2つが成り立つ。

3. $X_1 + X_2 + \cdots + X_n$は$N(n \mu, n \sigma^2)$に従う。

4. $\overline{X} = \cfrac{X_1 + X_2 + \cdots + X_n}{n}$とするとき、$\overline{X}$は$N(\mu, \frac{\sigma^2}{n})$に従う。

正規分布の線形変換

$X$が正規分布$N(\mu, \sigma^2)$に従っているとき、その線形変換$Y = aX + b$は$N(a\mu + b, a^2 \sigma^2)$に従う。

(※証明は今後掲載予定・・・(。´･ω･)?)

正規分布の期待値

$E[X]$：$X$の期待値

$$E[X] = \mu$$(※計算過程は今後掲載予定・・・(。´･ω･)

正規分布の分散

$V[X]$：$X$の分散

$$V[X] = \sigma^2$$(※計算過程は今後掲載予定・・・(。´･ω･)

正規分布のモーメント母関数

$m(\theta) = E[e^{\theta X}]$：$X$のモーメント母関数

$$\begin{alignat*}{2} m(\theta) &= E[e^{\theta X}] \\ &= \exp (\mu \theta + \cfrac{1}{2} \sigma^2 \theta^2) \hspace{5mm} (- \infty < \theta < \infty) \end{alignat*}$$

標準正規分布

正規分布$N(\mu, \sigma^2)$に対して、変数変換$Z$を

$$Z = \cfrac{X - \mu}{\sigma}$$

とおく（この変換を標準化(standardixation)という）。このとき$Z$の確率密度関数$f(z)$は

$$f(z) = \cfrac{1}{\sqrt{2 \pi}} \exp \left( - \cfrac{ \ z^2 \ }{2} \right) \hspace{5mm} (- \infty < z < \infty)$$

となり、この確率密度関数$f(z)$を標準正規分布(standard normal distribution)といい、$N(0, 1)$と表せる。どんな正規分布も標準化を行うことにより標準正規分布となる。

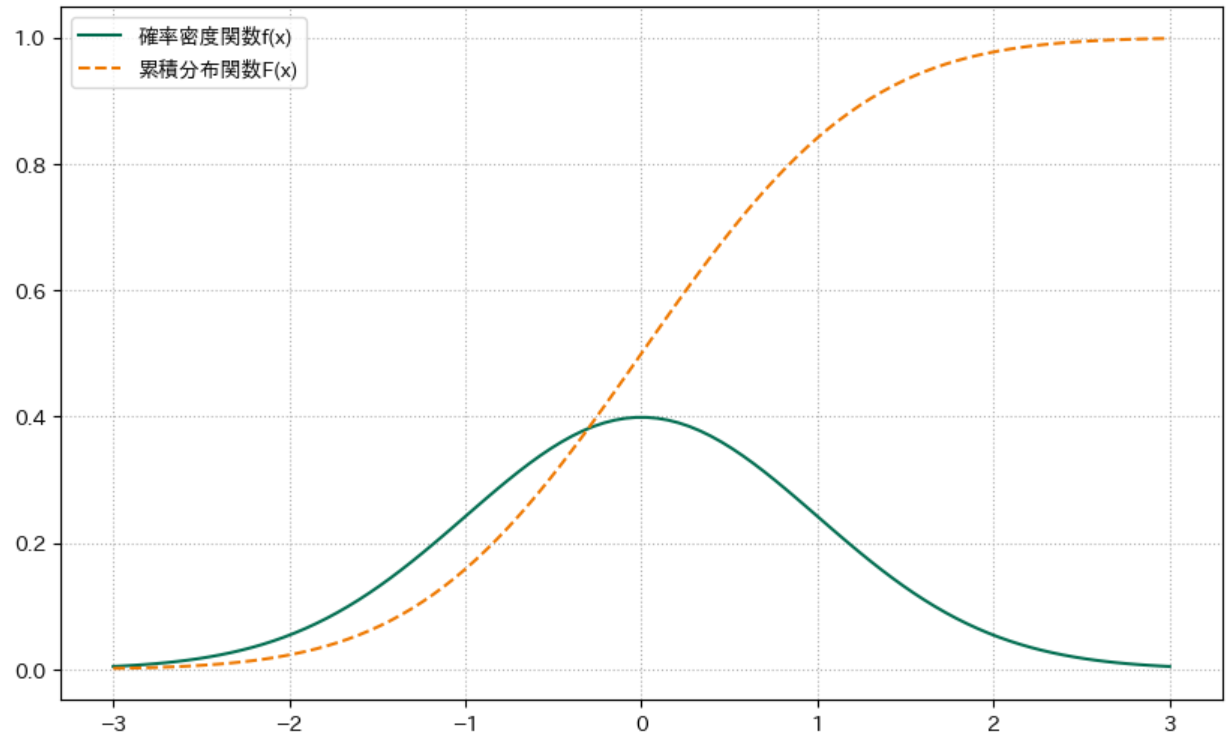
標準正規分布の確率密度関数

以後、標準正規分布の確率密度関数$f(z)$を$\varphi (z)$で表すこととする。

標準正規分布の累積分布関数

標準正規分布の累積分布関数$\Phi(z)$を以下のように定義する。

$$\begin{alignat*}{2} \Phi(z) &= P (Z \leqq z) \\ &= \int_{- \infty}^{z} \varphi (t) dt \\ &= \int_{- \infty}^{z} \cfrac{1}{\sqrt{2 \pi}} \exp \left( - \cfrac{ \ t^2 \ }{2} \right) dt, \hspace{5mm} Z ～ N(0, 1) \end{alignat*}$$

標準正規分布表

標準正規分布は、その便利さから確率変数$Z$と累積分布関数による確率との関係を一覧にした表が存在する。それが「標準正規分布表」である。その表が以下のとおりである。

$$\begin{alignat*}{2} Q(u) &= 1 - \Phi (u) \\ &= \int_{u}^{\infty} \varphi (t) dt \end{alignat*}$$

とするとき、$u$の値に対する確率$Q(u)$の値は以下のとおりである。
※行は$u$の一の位と小数第一位の値を表し、列は$u$の小数第二位の値を表している。

手作りしました 笑

後の例題の中でも、この標準正規分布を用いて問題を解いていきますが、その場合累積分布関数を用いて計算をしていきます。よって実際は以下のように式を変形していますので、ご注意ください。

$$\Phi (u) = 1 - Q(u)$$

例題

(「統計学実践ワークブック」より)
問6.1
あるテストの受験者は全部で1000人であり、受験者全体でのテストの得点の分布は正規分布$N(65, 10^2)$で近似できるとする。このテストでA君は85点、B君は60点であった。なお、標準正規分布$N(0, 1)$の確率密度関数$f(z) = \frac{1}{\sqrt{2 \pi}} \exp \left( - \frac{z^2}{2} \right)$である。
[1] A君およびB君の偏差値はいくらか。
[2] A君の得点とB君の得点の間に入る受験者の人数はおおよそ何人か。
[3] このテストの全受験者の得点の箱ひげ図を描いた場合、四分位範囲（箱の長さ）はいくらか。
[4] このテストで65点以上の受験者のみを集めた場合、彼・彼女らの得点の平均値はおよそいくらか。

解答

[1] A君およびB君の偏差値はいくらか。

テストの得点を$X$とすると、題意より$X$は正規分布$N(65, 10^2)$に従う（つまり$X$～$N(65, 10^2)$である）。
ここで、一次変換

$$Z = \cfrac{X - 65}{10} \hspace{5mm} \cdots ①$$

とおけば、$Z$は標準正規分布$N(0, 1)$に従う（つまり$Z$～$N(0, 1)$である）。

ところで偏差値とは、正規分布$N(50, 10^2)$に従う確率変数である。つまり偏差値を確率変数$Y$とおくと、$Y$～$N(50, 10^2)$である。この$Y$と$Z$は次の一次変換の関係をもつ。

$$Y = 10Z + 50$$

ゆえに偏差値$Y$を求めるための得点$X$についての式は、

$$\begin{alignat*}{2} Y &= 10Z + 50 \\ &= 10 \times \cfrac{X - 65}{10} + 50 \end{alignat*}$$

であるから、求めるA君の偏差値は、A君の得点が$X = 85$より

$$\begin{alignat*}{2} Y &= 85 - 65 + 50 \\ &= 85 - 15 \\ &= \underline{70} \end{alignat*}$$

またB君は$X = 60$なので$\underline{Y = 45}$

偏差値の式
テストなどでよく見かける偏差値ですが、一般的には以下の式で知られていると思います。

データ$x_i \ (i = 1, 2, \cdots, n)$があるとき、$x_i$に対する偏差値SS(Standard Score)とは、

$$SS = 10 \times \cfrac{x_i - 平均値}{標準偏差} + 50$$

この式は、全国模試や共通テストなどの試験の場合は特に問題にはならないと思います。なぜならば正規分布に従っている可能性が高いからです。
上の例題[1]の問題でわかる通り、偏差値の式の概念には正規分布（と、二段階の一次変換）が用いられています。ですから、本来ならば偏差値は正規分布に従っているという前提を踏まえなければなりません。しかし基本的に共通テストなどは正規分布に従うような試験になるように作成しているため、当然正規分布に従います（逆に従わない場合、テストの質が悪いことになります。）

しかし、学校の定期試験などでは話が別です。正規分布に従っているかを確認せず手当たり次第に偏差値を出しているケースがあちこちで見受けられますが、実際には不適切です。

[2] A君の得点とB君の得点の間に入る受験者の人数はおおよそ何人か。

テストの得点を標準化して解いていく（∵標準正規分布表を用いて計算したいから）。
まず、A君の得点を標準化した値を$z_A$とする。すると①より

$$\begin{alignat*}{2} z_A &= \cfrac{85 - 65}{10} \\ &= \cfrac{ \ 20 \ }{10} \\ &= 2 \end{alignat*}$$

である。同様にB君の得点を標準化した値を$z_B$とすると、

$$\begin{alignat*}{2} z_B &= \cfrac{60 - 65}{10} \\ &= \cfrac{ \ -5 \ }{10} \\ &= -0.5 \end{alignat*}$$

である。ゆえに、標準正規分布において$Z$の取りうる値が$-0.5$以上$2$以下となるような確率$P(-0.5 \leqq X \leqq 2)$は、

$$\begin{alignat*}{2} P(-0.5 \leqq Z \leqq 2) &= P(Z \leqq 2) - P(Z \leqq -0.5) \\ &= \Phi (2) - \Phi (-0.5) \\ &= \Phi (2) - (1 - \Phi (0.5)) \\ &= (1 - 0.0228) - (1 - (1 - 0.3085)) \\ & (標準正規分布表より) \\ &= (1 - 0.0228) - 0.3085 \\ &= 1 - 0.3313 \\ &= 0.6687 \end{alignat*}$$

となる。したがって求める受験者の人数は

$$\begin{alignat*}{2} & 1000 \times 0.6687 \\ =& 668.7 \\ \fallingdotseq& \underline{669（人）} \end{alignat*}$$

標準正規分布表の使い方

上記の中で$\Phi (2)$の値を標準正規分布表より求めています。
標準正規分布の定義より、以下の式が成り立っていました。

$$\Phi (u) = 1 - Q(u)$$

標準正規分布表には$Q(u)$の値が書かれているので、$u$の値に対応する$Q(u)$の値を探します。
すると以下のようになります。

今回、$u$の値が$2 = 2.00$であるため、「行が2.0」であり、「列が0.00」となる値を探しに行きます。すると、$Q(u) = 0.02275$を得ることができます。
※「おい！値が違うぞ！」と思うかもしれませんが、すいません。どうやら表によって採用する桁数が異なったりするため、若干誤差が生じます。実際の統計検定では試験時に必要な場合は標準正規分布表が渡されるので、そちらの値を元に算出してください。

[3] このテストの全受験者の得点の箱ひげ図を描いた場合、四分位範囲（箱の長さ）はいくらか。

四分位範囲は定義より

$$q_3 - q_1$$

である。ただし、$q_3, q_1$はそれぞれ

$$P(Z \leqq q_3) = 0.75 \\ P(Z \leqq q_1) = 0.25$$

を満たすものとする。よって、

$$\begin{alignat*}{2} & P(Z \leqq q_3) &= 0.75 \\ \Leftrightarrow & \Phi (q_3) &= 0.75 \\ \end{alignat*}$$

である。標準正規分布表より

$$q_3 = 0.67$$

である。ここで、

$$\begin{alignat*}{2} \cfrac{X - 65}{10} &= 0.67 \\ X &= 6.7 + 65 \\ X &= \underline{71.7} \end{alignat*}$$

同様に$P(z \leqq q_1) = 0.25$を求めるが、これは標準正規分布の対称性から

$$q_1 = - 0.67$$

である。よって、

$$\begin{alignat*}{2} \cfrac{X - 65}{10} &= -0.67 \\ X &= -6.7 + 65 \\ X &= \underline{58.8} \end{alignat*}$$

以上より、求める四分位範囲は

$$71.7 - 58.3 = \underline{13.4}$$

[4] このテストで65点以上の受験者のみを集めた場合、彼・彼女らの得点の平均値はおよそいくらか。

$E[X|X \geqq 65]$を求める。ここで、

$$\begin{alignat*}{2} Z &= \cfrac{X - 65}{10} \\ X &= 10Z + 65 \end{alignat*}$$

であるから、

$$\begin{alignat*}{2} E[X|X \geqq 65] &= E[10Z + 65|10Z + 65 \geqq 65] \\ &= E[10Z + 65|Z \geqq 0] \\ &= 65 + 10 E[Z|Z \geqq 0] \end{alignat*}$$

である。つまり$E[Z|Z \geqq 0]$を求めればよい。ここで、$Z \geqq 0$のもとでの$Z$の条件付き確率密度関数$f$は

$$\begin{alignat*}{2} f(Z|Z \geqq 0) &= \begin{cases} \cfrac{\varphi (z)}{f(Z \geqq 0)} & (z \geqq 0) \\ 0 & (z < 0) \\ \end{cases} \\ \end{alignat*}$$

であるので、

$$\begin{alignat*}{2} f(Z|Z \geqq 0) &= \int_{- \infty}^{\infty} z f(z|z \geqq 0) dz \\ &= \int_{- \infty}^{0} z \cdot 0 dz + \int_{0}^{\infty} z \cdot \cfrac{\varphi (z)}{f(Z \geqq 0)} dz \\ &= \int_{0}^{\infty} z \sqrt{\cfrac{ \ 2 \ }{\pi}} \ e^{- \frac{ \ z^2 \ }{2}} dz \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \int_{0}^{\infty} z \ e^{- \frac{ \ z^2 \ }{2}} dz \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \lim_{R \to \infty} \int_{0}^{R} \left( - e^{- \frac{ \ z^2 \ }{2}} \right)^{\prime} dz \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \lim_{R \to \infty} \left[ - e^{- \frac{ \ z^2 \ }{2}} \right]_{0}^{R} \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \lim_{R \to \infty} \left( - e^{- \frac{ \ R^2 \ }{2}} + 1 \right) \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \cdot \left( - 0 + 1 \right) \\ &= \sqrt{\cfrac{ \ 2 \ }{\pi}} \\ & \fallingdotseq 0.798 \end{alignat*}$$

以上より、

$$\begin{alignat*}{2} E[X|X \geqq 65] &= 65 + 10 E[Z|Z \geqq 0] \\ &= 65 + 10 \times 0.798 \\ &= 72.98 \\ & \fallingdotseq \underline{73} \end{alignat*}$$

参考資料

• 日本統計学会(編集).日本統計学会認定 統計検定準１級対応 統計学実践ワークブック.学術図書出版社.2020
• 東京大学教養学部統計学教室.統計学入門(基礎統計学Ⅰ).東京大学出版会.1991
• 小寺 平治.新統計入門.裳華房.1996
• 稲垣 宣生, 山根 芳知, 吉田 光雄.統計学入門.裳華房.1992
• 長瀬道弘・芦野隆一.微分積分概説.サイエンス社.2007
• 加藤文元.チャート式シリーズ 大学教養 微分積分.数研出版.2024

$\bf{\textcolor{red}{記事が役に立った方は「いいね」を押していただけると、すごく喜びます \ 笑}}$
ご協力のほどよろしくお願いします。