Zenn
📖

NumPyro：インストール方法と基本操作

2023/04/17に公開
Python
ppl
numpyro
tech

はじめに

PPLの中ではStanが使用されることが多いですが、「Stan言語で書かないといけない」「コンパイルに時間がかかる」等によりストレスがかかることが多かったので、PythonのNumpyライクに書くことができるNumPyroを触っています。個人的にNumpyを触っていればとっつきやすいため良いライブラリだと思うのですが、ネットの記事がほとんどないことがあまり広がらない要因の１つかなと思います。（また記事も古く情報が更新されてないこともあります）
そこで、日本語のNumPyroの記事が増えることに期待して、ドキュメント読んでもいまいち分からないところをカバーしながらまとめていきたいと思います。

予定記事

チュートリアル

  1. インストール方法と基本操作
    • インストール方法
    • distributions
    • 単回帰
  2. NumPyro特有の関数などまとめ
    • サンプルのShape
    • 確率分布の変換
    • numpyro.handlersの基本操作
    • その他：配列操作
  3. 基本のモデル
    • 重回帰
    • ポアソン回帰
    • 二項ロジスティック回帰
    • ロジスティック回帰
    • 外れ値回帰
    • 多項ロジスティック回帰
    • simplexベクトルとImproperUniform
    • 多変量正規分布
  4. 階層モデル
    • 単一の階層
    • 複数の階層
  5. 離散潜在変数の扱い方
    • Bernoulli分布
    • Poisson分布
    • 混合正規分布
    • ゼロ過剰ポアソン分布
  6. 再パラメータ化
    • Nealの漏斗
  7. 順序回帰と独自の分布の定義
    • ImproperUniform, Normal, Dirichletを事前分布に採用した順序回帰
    • 独自の分布の定義
  8. スパースモデル
    • Bayesian Lasso
    • 馬蹄事前分布を使用した回帰モデル
    • 正則化つき馬蹄事前分布を使用した回帰モデル
  9. 打ち切りデータの扱い方
    • Truncated Normal distribution
  10. 欠損値の扱い方
    • mask()の挙動
    • 連続値の場合
    • 離散潜在変数の場合
  11. ODE
    • 化学反応速度式の例
  12. 次元圧縮
    • ベイジアン主成分分析
    • automatic relevance determination(ARD)付き主成分分析
  13. ベイジアンABテスト
    • ベイジアンABテスト
  14. 各分布に関してまとめ
  15. ガウス過程
    • the marginal likelihood GP
    • the marginal likelihood GP + cholesky_decompose
    • the latent variable GP
  16. 時系列分析
    • scan関数について
    • 1階差分のトレンド項

実践

  1. 階層モデル系論文実装
  2. ガウス過程系（NumPyroは機能が揃ってないため、必要に応じてPyro+GPyTorchで実装）
  3. 状態空間モデル、Prophet

参考文献

随時追加します。

インストール方法

poetryで以下のtomlファイルを作成してインストールします。私の環境では後述するグラフィカルモデルを可視化するコードでエラーが出たため、numpyroをnumpyro = {git = "https://github.com/pyro-ppl/numpyro"}のようにgitからインストールしています。
funsorは離散潜在変数を自動で周辺化してくれる機能を使う際に必要なライブラリです。

poetry install
pyproject.toml
[tool.poetry]
name = "numpyro-intro"
version = "0.1.0"
description = ""
authors = ["yoshida"]
readme = "README.md"
packages = [{include = "numpyro_intro"}]

[tool.poetry.dependencies]
python = "^3.9"
numpyro = {git = "https://github.com/pyro-ppl/numpyro"}
pandas = "^1.5.3"
numpy = "^1.24.2"
matplotlib = "^3.7.1"
arviz = "^0.15.1"
jupyterlab = "^3.6.2"
seaborn = "^0.12.2"
ipywidgets = "^8.0.5"
flax = "^0.6.7"
graphviz = "^0.20.1"
funsor = "^0.4.5"


[build-system]
requires = ["poetry-core"]
build-backend = "poetry.core.masonry.api"

distributionの使い方

確率分布はnumpyro.distributionsにさまざまな種類の分布が格納されています。今回は代表的な分布である正規分布で使い方を見ていきます。

d.sample()により、１つ上の行で定義した平均0、標準偏差0.5の正規分布からサンプリングすることができます。ここで、最初の引数は乱数のシードでrandom.PRNGKey(0)を与えてあげます。これはjaxのお作法でして、こちらが参考になります。要はグローバルでシードを固定すると並列化して複数乱数を発生させたい時に再現性が取れず困ってしまうので、こういった記法になっているようです。

from jax import random
import jax.numpy as jnp
import numpyro.distributions as dist

d = dist.Normal(loc=0.0, scale=0.5)
samples = d.sample(random.PRNGKey(0), sample_shape=(10,))
samples

Array([-0.18605545,  0.13211557, -0.09126384, -0.36840984, -0.22015189,
       -0.0760721 , -0.33567673, -0.29543206,  0.36584443,  0.2836513 ],      dtype=float32)

また、d.log_prob(value)により任意の値に対して生成確率の対数値を計算することができます。

jnp.exp(d.log_prob(0))

Array(0.7978846, dtype=float32, weak_type=True)

単回帰

細かい操作を見てもイメージできないので簡単な単回帰から見ていきます。

データの準備

書籍「StanとRでベイズ統計モデリング」のデータを使用します。以下のリンクからcloneしてください。
https://www.kyoritsu-pub.co.jp/book/b10003786.html
https://github.com/MatsuuraKentaro/RStanBook

ライブラリのインポート

特に解説はないですが、私はCPU環境で計算を流しているのでnumpyro.set_platform("cpu") numpyro.set_host_device_count(1)で環境とCPUの数を指定しています。

import os

import jax.numpy as jnp
from jax import random
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import numpyro
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
import numpyro.distributions.constraints as constraints
from numpyro.infer import MCMC, NUTS
from numpyro.infer import Predictive
from numpyro.infer import init_to_feasible
from numpyro.infer.util import initialize_model

import arviz as az

az.style.use("arviz-darkgrid")

assert numpyro.__version__.startswith("0.11.0")

numpyro.set_platform("cpu")
numpyro.set_host_device_count(1)

データ読み込み

chapter04のデータ（chap04/input/data-salary.txt）を使用します。Xが年齢でYが給料を記録したもので、XとYには正の相関があります。

df = pd.read_csv("./RStanBook/chap04/input/data-salary.txt")
sns.scatterplot(x=df["X"], y=df["Y"])

モデルの定義

今回は単純に正の相関が見られるので、単回帰でモデリングします。NumPyroで書くと以下のようになります。（※ Stanと異なり事前分布を何かしら指定してあげる必要がありますが、ここでは雑に書いているので注意してください）

def model(x, y=None):
    # 切片
    intercept = numpyro.sample("intercept", dist.Normal(0, 100))
    # 重み
    coef = numpyro.sample("coef", dist.Normal(0, 100))
    # muを計算
    mu = coef*x + intercept
    
    # ノイズ
    sigma = numpyro.sample("sigma", dist.Uniform(0, 100))
    
    # 正規分布からのサンプリングyは観測値なので、obs=yを追加
    with numpyro.plate("N", len(x)):
        numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)

なんとなくイメージは掴めるのではないかなと思いますが最後の２行だけ説明します。

numpyro.plate

numpyro.plateはコンテキスト内にある確率変数を条件付き独立で指定した数（ここでは５個）だけ生成されます。

with numpyro.plate("N", 5): 
    d = dist.Normal(0, 1)
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))
# イメージとしては以下と同じ
# for i in range(5):
#     numpyro.sample(f"a{i}", d, rng_key=key)

print(samples)
print(samples.shape)

[ 0.18784384 -1.2833426  -0.2710917   1.2490594   0.24447003]
(5,)

obs=y

観測した値がある確率変数では、numpyro.sample(name, dist, obs=data)とします。obs=dataと指定することで観測された値がモデルで使用され、obs=Noneだと確率分布から適当な値がサンプリングされ使用されます。

モデルの描画

NumPyroではグラフィカルモデルを描画することができます。上記で定義したモデルが想定通りになっているか見てみましょう。

numpyro.render_model(
    model=model, 
    model_kwargs={"x": df["X"].values, "y": df["Y"].values}, 
    render_params=True, 
    render_distributions=True
)

上記でも最低限問題ないですが、より詳細に書き込みたい場合はモデルを以下のように修正します。

def model(x, y=None):
    # 各パラメータを定義
    i_mu = numpyro.param("i_mu", 0., constraint=constraints.real)
    i_scale = numpyro.param("i_scale", 100., constraint=constraints.real)
    c_mu = numpyro.param("c_my", 0., constraint=constraints.real)
    c_scale = numpyro.param("c_scale", 100., constraint=constraints.real)
    sigma_u = numpyro.param("sigma_u", 100., constraint=constraints.positive)
    
    # 切片
    intercept = numpyro.sample("intercept", dist.Normal(i_mu, i_scale))
    # 重み
    coef = numpyro.sample("coef", dist.Normal(c_mu, c_scale))
    # muを計算
    mu = numpyro.deterministic("mu", coef*x + intercept)
    
    # ノイズ
    sigma = numpyro.sample("sigma", dist.Uniform(0, sigma_u))
    
    # 正規分布からのサンプリング.yは観測値なので、obs=yを追加
    with numpyro.plate("N", len(x)):
        numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)

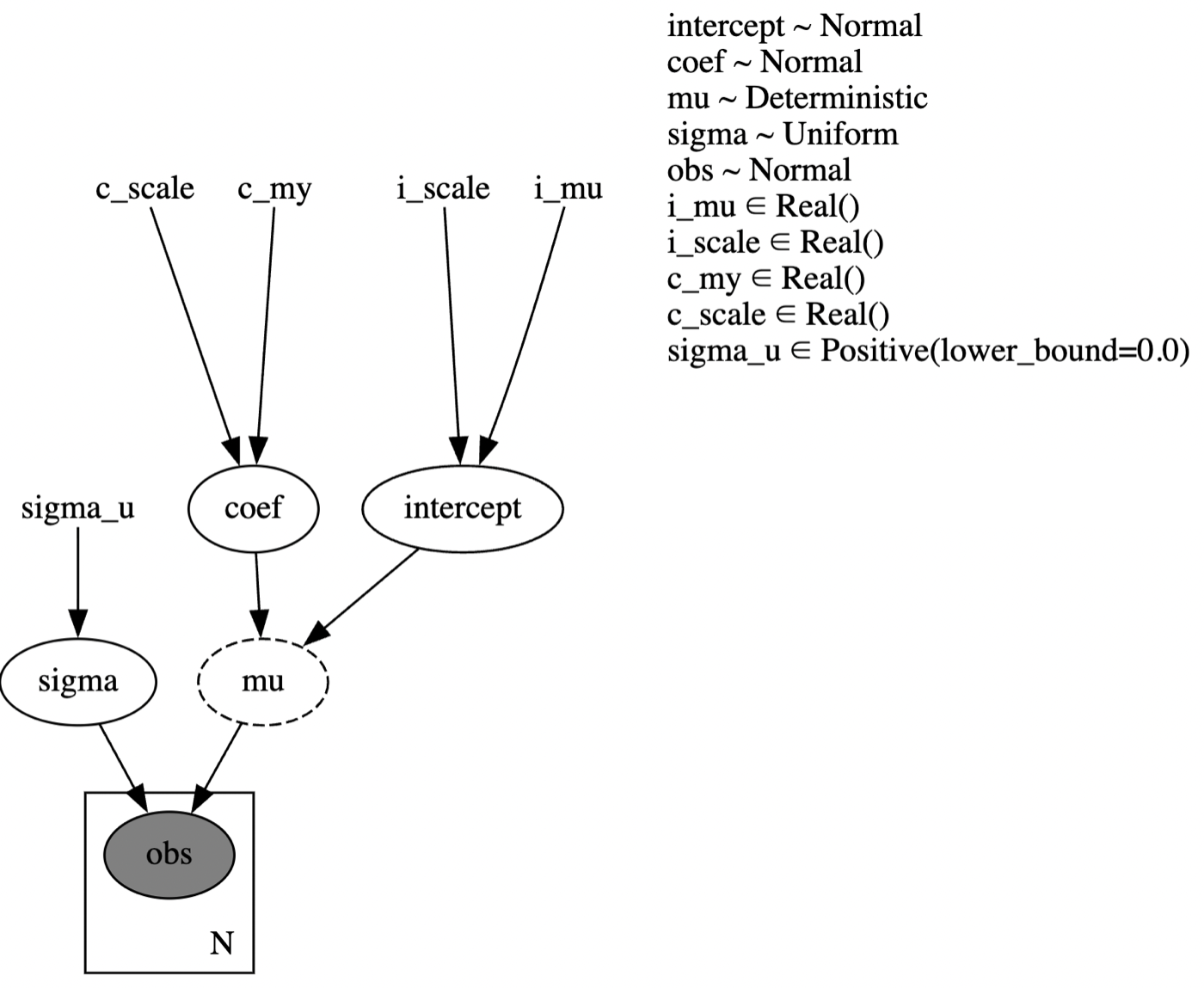
再度レンダリングします。ここまで書くとかなりわかりやすい図になりますね。numpyro.paramで指定するのはめんどくさいですが、明示的に最適化するパラメータであることを示すことでこのようなメリットがあります。また、numpyro.deterministic()は本来は情報（ここでは途中計算のmu）を記録しておく関数なのですが、わざわざ使用することでレンダリングする際には点線で囲まれて表示させることができます。

numpyro.render_model(
    model=model, 
    model_kwargs={"x": df["X"].values, "y": df["Y"].values}, 
    render_params=True, 
    render_distributions=True
)

MCMC

推論は以下の数行で実行できます。今回はNUTSを使用して推論します。ここでは引数としてinit_strategy=init_to_feasibleとadapt_step_size=Trueを指定しています。前者は初期化の方法でデフォルト値よりN_effの数が増えることが多いです。後者はハイパーパラメータのステップサイズをwarmup期間に自動で調整してくれます。
mcmc.run()は第一引数に再現性を取るためのrandom.PRNGKeyを与え、残りの引数は modelで指定した引数を与えます。

# 乱数の固定に必要
rng_key= random.PRNGKey(0)

# NUTSでMCMCを実行する
kernel = NUTS(model, init_strategy=init_to_feasible, adapt_step_size=True) # init_to_feasibleにするとN_effが増える
mcmc = MCMC(kernel, num_warmup=1000, num_samples=2000, num_chains=4, thinning=1)
mcmc.run(
    rng_key=rng_key,
    x=df["X"].values,
    y=df["Y"].values,
)

結果の確認

各パラメータの統計量

mcmc.print_summary()

結果の取得

numpyro.deterministic()を使用していた場合は、指定したmuも同時に記録されていることが確認できます。また、得られるサンプル数としては「num_samples*num_chains」で8000個得られています。

samples = mcmc.get_samples()

print(samples.keys())
print(samples["coef"].shape)

dict_keys(['coef', 'intercept', 'mu', 'sigma'])
(8000,)

Arvizによる可視化

他のライブラリと同様にArvizにより可視化も簡単です。

numpyro2az = az.from_numpyro(mcmc)
az.plot_trace(numpyro2az, figsize=(8,4));

予測結果の可視化

muの可視化

muを可視化してみます。今回はnumpyro.deterministic()で記録しているのでsamplesから取り出すだけですね。

posterior_mu = samples["mu"]
print(posterior_mu.shape)

mean_mu = posterior_mu.mean(axis=0)
print(mean_mu.shape)

hpdi_mu = hpdi(posterior_mu, 0.9)
print(hpdi_mu.shape)

def plot_regression(x, y_act, y_mean, y_hpdi):
    # Sort values for plotting by x axis
    idx = jnp.argsort(x)
    x_sorted = x[idx]
    y_sorted = y_act[idx]
    y_mean_sorted = y_mean[idx]
    hpdi_sorted = y_hpdi[:, idx]
    
    # Plot
    fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 4))
    ax.plot(x_sorted, y_mean)
    ax.plot(x_sorted, y_sorted, "o")
    ax.fill_between(x_sorted, hpdi_sorted[0], hpdi_sorted[1], alpha=0.3, interpolate=True)
    return ax

ax = plot_regression(df["X"].values, df["Y"].values, mean_mu, hpdi_mu)
ax.set(
    xlabel="Age", ylabel="Salary", title="Regression line with 90% CI"
);

obsの可視化

NumPyroに用意されているPredictive()を使用することで簡単に計算できます。今回は事後分布から計算したいので、事後分布のサンプルsamplesをPredictive()の引数に与えます。次にpredictive(rng_key_, x=df["X"].values)["obs"]のように引数にxだけ与えてy=Noneにするとyが生成されます。model関数の引数でy=Noneにしていたのはこのためでした。（意味ないですが、predictive(rng_key_, x=df["X"].values, y=df["Y"].values)["obs"]にすると観測値がそのまま得られます）

rng_key, rng_key_ = random.split(rng_key)
predictive = Predictive(model, samples)
predictions = predictive(rng_key_, x=df["X"].values)["obs"]
print(predictions.shape)

posterior_mu = predictions

mean_mu = posterior_mu.mean(axis=0)
print(mean_mu.shape)

hpdi_mu = hpdi(posterior_mu, 0.95)
print(hpdi_mu.shape)

def plot_regression(x, y_act, y_mean, y_hpdi):
    # Sort values for plotting by x axis
    idx = jnp.argsort(x)
    x_sorted = x[idx]
    y_sorted = y_act[idx]
    y_mean_sorted = y_mean[idx]
    hpdi_sorted = y_hpdi[:, idx]
    
    # Plot
    fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 4))
    ax.plot(x_sorted, y_mean)
    ax.plot(x_sorted, y_sorted, "o")
    ax.fill_between(x_sorted, hpdi_sorted[0], hpdi_sorted[1], alpha=0.3, interpolate=True)
    return ax

ax = plot_regression(df["X"].values, df["Y"].values, mean_mu, hpdi_mu)
ax.set(
    xlabel="Age", ylabel="Salary", title="Regression line with 90% CI"
);

事前分布からのサンプリング

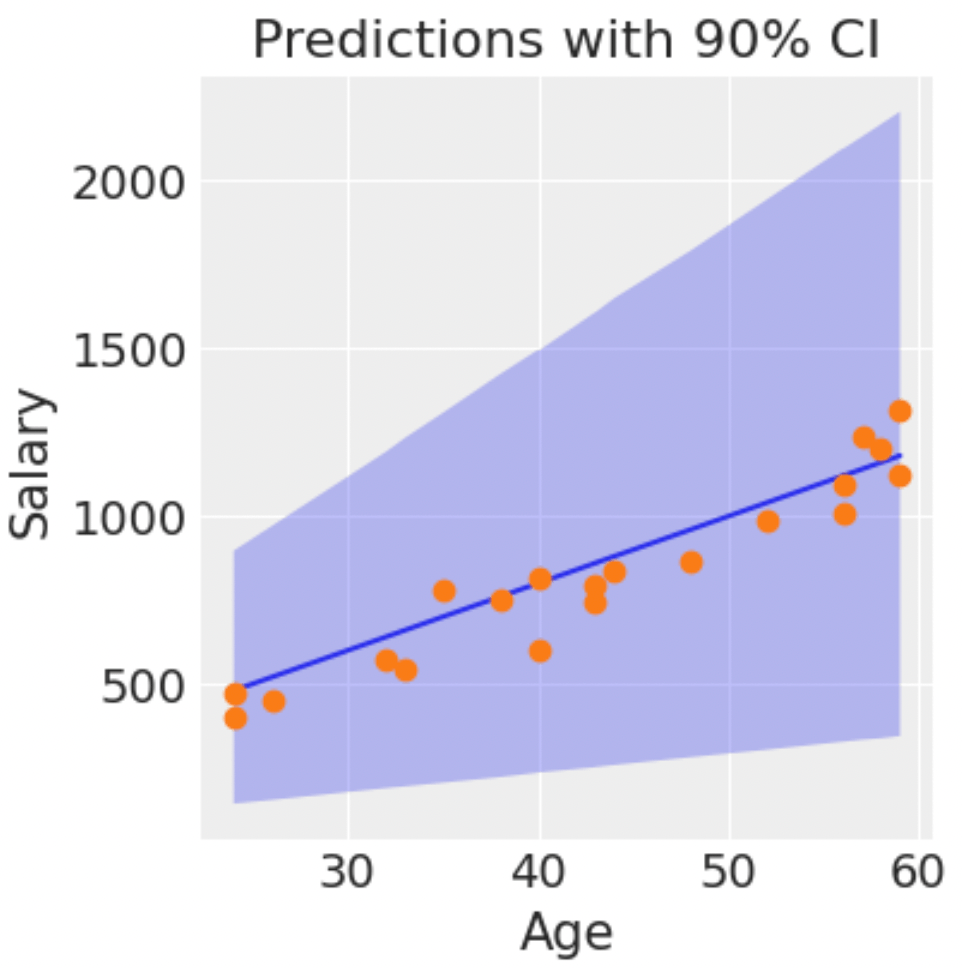
事前分布やモデルの妥当性を大まかに確認するために事前分布からサンプリングしシミュレーションします。今は何も考えていない事前分布を設定したので、かなり幅広い範囲をカバーしており現実的に考慮しなくてもいい範囲まで存在していることがわかります。。これを事前の相関や最尤推定を行った後の知見を考慮したモデルにすると、データが少ない場合でも現実に近いより妥当なモデルに反映されやすくなります。

方法としては上記でも使用したPredictive()を使用することで事前分布からのサンプリングも簡単にできます。Predictive(model, num_samples=100)のようにsamplesを与えず生成するサンプルの数だけ指定します。

rng_key, rng_key_ = random.split(rng_key)
prior_predictive = Predictive(model, num_samples=100)
prior_predictions = prior_predictive(rng_key_, x=df["X"].values)["obs"]
mean_prior_pred = jnp.mean(prior_predictions, axis=0)
hpdi_prior_pred = hpdi(prior_predictions, 0.9)

ax = plot_regression(df["X"].values, df["Y"].values, mean_prior_pred, hpdi_prior_pred)
ax.set(
    xlabel="Age", ylabel="Salary", title="Predictions with 90% CI"
);

より現実の知見を加えた事前分布に修正して再度実行します。先ほどと比べて現実の範囲に収まっているように思えます。

def model_2(x, y=None):
    # 切片
    intercept = numpyro.sample("intercept", dist.Normal(0.0, 10))
    # 重み
    coef = numpyro.sample("coef", dist.Normal(20.0, 10))
    # muを計算
    mu = coef*x + intercept
    # ノイズ
    sigma = numpyro.sample("sigma", dist.Exponential(1.0))
    
    # 正規分布からのサンプリング.yは観測値なので、obs=yを追加
    numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)

rng_key, rng_key_ = random.split(rng_key)
prior_predictive = Predictive(model_2, num_samples=100)
prior_predictions = prior_predictive(rng_key_, x=df["X"].values)["obs"]
mean_prior_pred = jnp.mean(prior_predictions, axis=0)
hpdi_prior_pred = hpdi(prior_predictions, 0.9)

ax = plot_regression(df["X"].values, df["Y"].values, mean_prior_pred, hpdi_prior_pred)
ax.set(
    xlabel="Age", ylabel="Salary", title="Predictions with 90% CI"
);

最後に

以上で「インストール方法と基本操作」は終わりです。とりあえずPythonに慣れた人がとっつきやすいと感じてもらえていたら幸いです。

Discussion