🎃

NumPyro：NumPyro特有の関数などまとめ

2023/04/18に公開

Python

numpyro

tech

連載している記事の１つです。以前までの記事を読んでいる前提で書いているので、必要であればNumPyroの記事一覧から各記事を参考にしてください。

はじめに

NumPyroを用いてモデリングを実装する上で必要な知識をまとめて説明します。

ライブラリのインポート

import os

import jax.numpy as jnp
from jax import random
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns

import numpyro
from numpyro.diagnostics import hpdi
import numpyro.distributions as dist
import numpyro.distributions.constraints as constraints
from numpyro.infer import MCMC, NUTS
from numpyro.infer import Predictive
from numpyro.infer.util import initialize_model

import arviz as az

az.style.use("arviz-darkgrid")

assert numpyro.__version__.startswith("0.11.0")

numpyro.set_platform("cpu")
numpyro.set_host_device_count(1)

サンプルのShape

分布からサンプリングされたサンプルにはsample_shapeとbatch_shape, event_shapeの３種類あります。

sample_shape

sample_shapeはサンプル全体の形状を表します。以下のコードのようにsample_shapeはsample_shape = batch_shape + event_shapeと表すことができます。そのため、以降では今後のモデリングの実装で必須となるbatch_shapeとevent_shapeの２つに関して説明します。

d = dist.Normal(jnp.array([0]), jnp.array([1]))

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(f"sum batch and event shape: {d.batch_shape + d.event_shape}")
print(f"log_prob: {d.log_prob(0)}")

batch shape: (1,)
event shape: ()
samples: [-0.20584226]
sample shape: (1,)
sum batch and event shape: (1,)
log_prob: [-0.9189385]

batch_shape

NumPyroでは同時に複数の分布を定義し使用することができます。これらは同時に定義しているだけでお互いに独立にサンプリングされたものになります。この時の形状のことをbatch_shapeと呼びます。コードとしては以下のように２通りの書き方があるので、好きな方を選択してください。

パラメータに配列を渡す

d = dist.Normal(jnp.zeros(3), jnp.ones(3))

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(f"log_prob: {d.log_prob(0)}")

batch shape: (3,)
event shape: ()
samples: [ 1.8160863  -0.48262316  0.33988908]
sample shape: (3,)
log_prob: [-0.9189385 -0.9189385 -0.9189385]

expand()を使用する

expand()の引数に形状を表すイテラブルなオブジェクトを渡すことで同じパラメータの分布（ここでは、dist.Normal(0,1)）を形状の数だけ同時に作成することができます。

# expandと同じ意味
d = dist.Normal(0, 1).expand([3])

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(f"log_prob: {d.log_prob(0)}")

batch shape: (3,)
event shape: ()
samples: [ 1.8160863  -0.48262316  0.33988908]
sample shape: (3,)
log_prob: [-0.9189385 -0.9189385 -0.9189385]

event_shape

NumPyroでは、確率分布の従属変数の数（サンプリングされる次元数）の形状の情報を持ちます。この形状のことをevent_shapeと呼びます。例えば、２次元正規分布ではevent_shape=(2,)になりますし、１次元正規分布ではevent_shape=()になります。

とりあえず、３次元の正規分布を既存のクラスdist.MultivariateNormalを使用して作成し、event_shapeを確認してみます。

# １つの３次元正規分布を作る
d = dist.MultivariateNormal(jnp.zeros(3), jnp.eye(3))

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
# 3次元正規分布なので、valueとして３次元のArrayを渡している
print(f"log_prob: {d.log_prob(jnp.zeros(3))}") 
# 全部同じ値として以下でも同じ結果になる
print(f"log_prob: {d.log_prob(0)}")

batch shape: ()
event shape: (3,)
samples: [ 1.8160863  -0.48262316  0.33988908]
sample shape: (3,)
log_prob: -2.7568154335021973
log_prob: -2.7568154335021973

to_event()

上記では既存のクラスdist.MultivariateNormalを使用しましたが、NumPyroでは正規分布のような代表的な分布以外でも１次元の確率分布を組み合わせて多次元の確率分布を定義することができます。

以下では、expand([3])により３つの１次元正規分布を作った後に、to_event(1)によりbatch_shapeの右から１つ目（以降）の次元をevent_shapeとして扱っています。その結果、上記の既存のクラスdist.MultivariateNormalを使用した結果と同じ結果になっていることが確認できます。

# to_event(1)により、batch_shapeの右から1つ目の次元をeventとして扱う -> ３つの１次元正規分布から１つの3次元正規分布
d = dist.Normal(jnp.array([0]), jnp.array([1])).expand([3]).to_event(1)

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(f"log_prob: {d.log_prob(jnp.zeros(3))}")

batch shape: ()
event shape: (3,)
samples: [ 1.8160863  -0.48262316  0.33988908]
sample shape: (3,)
log_prob: -2.7568154335021973

次にto_event()の挙動を正しく理解するために、もう少し複雑な例を見ていきます。まずは、expand([3, 4])とすることで(3, 4)の計12個の独立した正規分布を作成しています。

d = dist.Normal(jnp.array([0]), jnp.array([1])).expand([3, 4])
#d = dist.Normal(jnp.zeros([3, 4]), jnp.ones([3, 4]))

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(d.log_prob(0))

batch shape: (3, 4)
event shape: ()
samples: [[ 1.1901639  -1.0996888   0.44367844  0.5984697 ]
 [-0.39189556  0.69261974  0.46018356 -2.068578  ]
 [-0.21438177 -0.9898306  -0.6789304   0.27362573]]
sample shape: (3, 4)
[[-0.9189385 -0.9189385 -0.9189385 -0.9189385]
 [-0.9189385 -0.9189385 -0.9189385 -0.9189385]
 [-0.9189385 -0.9189385 -0.9189385 -0.9189385]]

ここで、to_event(1)とto_event(2)の結果を確認してみます。

to_event(1)

to_event(1)によりbatch_shapeの右から１つ目（以降）の次元をevent_shapeとして扱っているので、batch_shape=(3, 4)の4がevent_shapeとして扱われることになります。そのため、4次元正規分布を３つ同時に定義したことになります。

d = dist.Normal(jnp.array([0]), jnp.array([1])).expand([3, 4]).to_event(1)

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(d.log_prob(jnp.zeros(4)))

batch shape: (3,)
event shape: (4,)
samples: [[ 1.1901639  -1.0996888   0.44367844  0.5984697 ]
 [-0.39189556  0.69261974  0.46018356 -2.068578  ]
 [-0.21438177 -0.9898306  -0.6789304   0.27362573]]
sample shape: (3, 4)
[-3.675754 -3.675754 -3.675754]

to_event(2)

to_event(2)によりbatch_shapeの右から2つ目以降の次元をevent_shapeとして扱っているので、batch_shape=(3, 4)の(3, 4)がevent_shapeとして扱われることになります。そのため、(3, 4)次元の正規分布を1つ定義したことになります。

d = dist.Normal(jnp.array([0]), jnp.array([1])).expand([3, 4]).to_event(2)

samples = d.sample(random.PRNGKey(0))
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")
print(d.log_prob(jnp.zeros((3,4))))

batch shape: ()
event shape: (3, 4)
samples: [[ 1.1901639  -1.0996888   0.44367844  0.5984697 ]
 [-0.39189556  0.69261974  0.46018356 -2.068578  ]
 [-0.21438177 -0.9898306  -0.6789304   0.27362573]]
sample shape: (3, 4)
-11.027262

numpyro.plateとshape

前回の記事の単回帰の例でもnumpyro.plateを触りましたが、より複雑なモデルになった際に混乱する原因になるので、numpyro.plateとshapeに関してここで説明します。

numpyro.plate

numpyro.plateはコンテキスト内でサンプリングされた事象はお互いに条件付き独立であることを明示的に伝える役割があります。これにより内部で処理がベクトル化され高速に処理されることになります。

２つ目の引数であるsizeでコンテキスト内でサンプリングする際に自動的にsizeの数だけ並列化されることになります。また、３つ目の引数のdimにより、numpyro.plateの次元に使用される次元を指定しています。デフォルトでは、batch_shape内の使用可能な一番右側の次元に自動的に割り当てられます。使用可能なという点に注意が必要で既に１より大きい形状を持つ次元だった場合はエラーが出ます。何を言ってるかわかりづらい箇所だと思うので、下の例を見ていきます。

基本の使い方

分布の定義などは先ほどの例と同じですが、コンテキスト内で書かれているのでsize=5だけ並列にサンプリングされ、最終的に得られているsample_shapeは5になっていることが分かります。また、今回の場合with numpyro.plate("N", 5, dim=-1): としてもbatch_shape=(1,)の一番右側の1がプレートに使用される次元になるので結果は変わりません。

with numpyro.plate("N", 5): 
    d = dist.Normal(jnp.array([0]), jnp.array([1]))
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))

print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")

batch shape: (1,)
event shape: ()
samples: [ 0.18784384 -1.2833426  -0.2710917   1.2490594   0.24447003]
sample shape: (5,)

dim=-2の場合

上記の例でdim=-2の場合を見ていきます。batch_shapeは(1,)しかないですが、dim=-2と指定することで右から2番目、つまり新しい軸を作ることになります。ここでは、sample_shape=(5, 1)になっており、縦のArrayを得ることができたことを確認できます。

with numpyro.plate("N", 5, dim=-2): 
    d = dist.Normal(jnp.array([0]), jnp.array([1]))
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))

print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")

batch shape: (1,)
event shape: ()
samples: [[ 0.18784384]
 [-1.2833426 ]
 [-0.2710917 ]
 [ 1.2490594 ]
 [ 0.24447003]]
sample shape: (5, 1)

多次元分布の場合

一応、event_shapeはplateの次元として割り当てられないということを以下のコードで確認しておきましょう。

with numpyro.plate("N", 5): 
    d = dist.MultivariateNormal(jnp.zeros(3), jnp.eye(3))
    #d = dist.Normal(jnp.zeros(3), jnp.ones(3)).to_event(1)
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))

print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")

batch shape: ()
event shape: (3,)
samples: [[ 0.08482574  1.9097648   0.29561743]
 [ 1.120948    0.33432344 -0.82606775]
 [ 0.6481277  -1.0353061  -0.7824839 ]
 [-0.4539462   0.6297971   0.81524646]
 [-0.32787678 -1.1234448  -1.6607416 ]]
sample shape: (5, 3)

多次元分布の場合でもdim=-2にしてみます。この場合はbatch_shape=(5, 1)でevent_shape=(3,)なので、sample_shape=batch_shape+event_shape=(5, 1, 3)になります。

with numpyro.plate("N", 5, dim=-2): 
    d = dist.MultivariateNormal(jnp.zeros(3), jnp.eye(3))
    #d = dist.Normal(jnp.zeros(3), jnp.ones(3)).to_event(1)
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))

print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")

batch shape: ()
event shape: (3,)
samples: [[[ 0.08482574  1.9097648   0.29561743]]

 [[ 1.120948    0.33432344 -0.82606775]]

 [[ 0.6481277  -1.0353061  -0.7824839 ]]

 [[-0.4539462   0.6297971   0.81524646]]

 [[-0.32787678 -1.1234448  -1.6607416 ]]]
sample shape: (5, 1, 3)

plateのネスト

plateをネストしてあげる必要が出て来る場合もあります。以下の例を見ていきましょう。複雑ですが、初めのwith numpyro.plate("N", 2, dim=-2): でsample_shape=(2, 1)のArrayが作成され、その後のwith numpyro.plate("K", 5, dim=-1):でsample_shape=(2, 1)の一番右側がplateに割り当てられて最終的にsample_shape=(2, 5)になります。

d = dist.Normal(jnp.array([0]), jnp.array([1]))
with numpyro.plate("N", 2, dim=-2): 
    samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))
    
    with numpyro.plate("K", 5, dim=-1):
        samples_k = numpyro.sample("b", d, rng_key=random.PRNGKey(0)) 

print("samples -----------------------")
print(f"batch shape: {d.batch_shape}")
print(f"event shape: {d.event_shape}")
print(f"samples: {samples}")
print(f"sample shape: {samples.shape}")

print("samples_k ----------------------")
print(f"samples: {samples_k}")
print(f"sample shape: {samples_k.shape}")

samples -----------------------
batch shape: (1,)
event shape: ()
samples: [[-0.78476596]
 [ 0.85644484]]
sample shape: (2, 1)
samples_k ----------------------
samples: [[-0.3721109   0.26423115 -0.18252768 -0.7368197  -0.44030377]
 [-0.1521442  -0.67135346 -0.5908641   0.73168886  0.5673026 ]]
sample shape: (2, 5)

確率分布の変換

dist.trandoformsを使用することで既存の分布に何かしらの処理を加えた分布からのサンプリングが可能になります。これにより、独自の課題にあった名前のない分布を作り出すことも可能です。
ここでは、代表的な変換のみを扱います。

dist.transforms.AffineTransform

分布を平行移動させます。

transformed_normal = dist.TransformedDistribution(
    base_distribution=dist.Normal(0., 0.5),
    # 平行移動する y = loc + sclae * x
    transforms=dist.transforms.AffineTransform(loc=1.0, scale=2.0)
)

samples = transformed_normal.sample(random.PRNGKey(0), (1000,))
sns.distplot(samples)

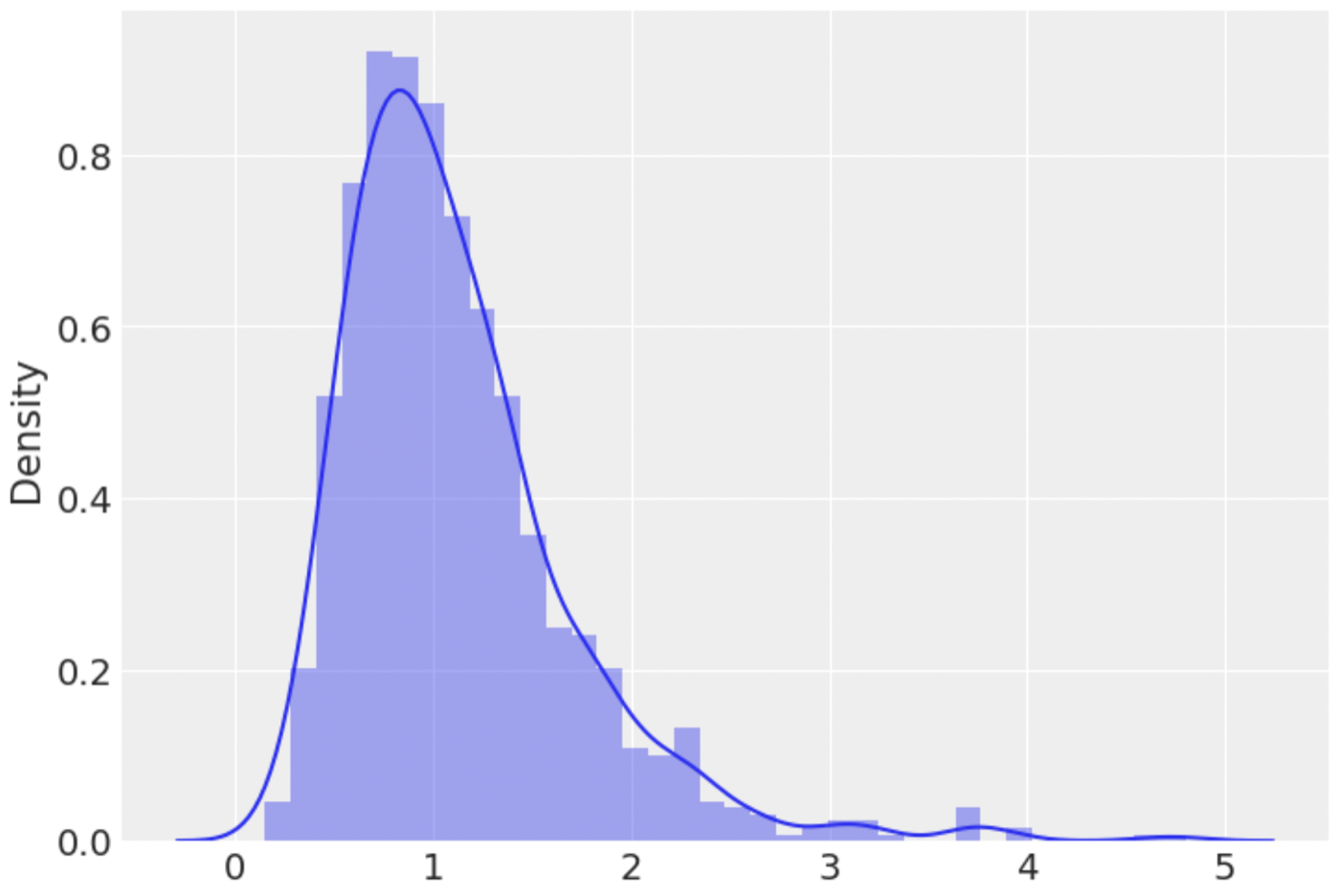
dist.transforms.ExpTransform

指数変換させます。

log_normal = dist.TransformedDistribution(
    base_distribution=dist.Normal(0., 0.5),
    transforms=dist.transforms.ExpTransform()
)

samples = log_normal.sample(random.PRNGKey(0), (1000,))
sns.distplot(samples)

numpyro.handlersの基本操作

NumPyroの内部で動作している機能としてnumpyro.handlersがあります。NumPyroのチュートリアルやより凝った操作をする際に知っておく必要があるので、一部の機能の基本操作を説明します。

インポート

from numpyro.handlers import seed, trace, condition, block

seed

NumPyroはJaxを使用しており、JAXは関数型疑似乱数生成器を使用しています。そのため、すべての確率関数にシードPRNGKey()を渡す必要があります。そこで、シードハンドラによって、関数内でsample()を呼び出すたびに、引数で与えた初期シードが分割され、以降の呼び出しでPRNGKeyを明示的に渡すことなく、新しいシードが使用されることになります。

def model(x, y=None):
    low, upper = -10000, 10000
    intercept = numpyro.sample("intercept", dist.Uniform(low, upper))
    coef = numpyro.sample("coef", dist.Uniform(low, upper))
    sigma = numpyro.sample("sigma", dist.Uniform(0, upper))
    
    mu = numpyro.deterministic("mu", coef*x + intercept)
    with numpyro.plate("N", len(x)):
        y_ = numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)
        
    return y_

# seedにより、rngkeyを各関数に渡さなくてもOK。また、returnでobs=yのy_が返されているので、outputは入力のyと等しい
output = seed(model, random.PRNGKey(0))(x=df["X"].values, y=df["Y"].values)
assert (output == df["Y"].values).all()

trace

sampleやdetermisticなどprimitive関数の入出力が記録されるようになります。

def model(x, y=None):
    low, upper = -10000, 10000
    intercept = numpyro.sample("intercept", dist.Uniform(low, upper))
    coef = numpyro.sample("coef", dist.Uniform(low, upper))
    sigma = numpyro.sample("sigma", dist.Uniform(0, upper))
    
    mu = numpyro.deterministic("mu", coef*x + intercept)
    with numpyro.plate("N", len(x)):
        y_ = numpyro.sample("obs", dist.Normal(mu, sigma), obs=y)
        
    return y_

trace_model = trace(seed(model, random.PRNGKey(0))).get_trace(x=df["X"].values, y=df["Y"].values)
print(trace_model.keys())

odict_keys(['intercept', 'coef', 'sigma', 'mu', 'N', 'obs'])

condition

conditionハンドラを用いてモデル内の各確率変数の実現値を固定（条件付け）してサンプリングを行うことが可能になります。条件付けはkeyを確率変数名、valueを固定する実現値としたdictionary型でconditionハンドラに渡します。このconditionハンドラを用いると、例えば、確率モデルの全ての確率変数の実現値を固定した上でサンプリングし、その確率を求めると同時確率を求めらます。 https://pyro-book.data-hacker.net/docs/pyro_modeling/

上記のサイトを参考にしました。一応同じコードをNumPytoにしたものを載せておきます。

# https://programtalk.com/vs4/python/pyro-ppl/numpyro/test/contrib/test_infer_discrete.py/
from numpyro.distributions.util import is_identically_one

def log_prob_sum(trace):
    log_joint = jnp.zeros(())
    for site in trace.values():
        if site["type"] == "sample":
            value = site["value"]
            intermediates = site["intermediates"]
            scale = site["scale"]
            if intermediates:
                log_prob = site["fn"].log_prob(value, intermediates)
            else:
                log_prob = site["fn"].log_prob(value)

            if (scale is not None) and (not is_identically_one(scale)):
                log_prob = scale * log_prob

            log_prob = jnp.sum(log_prob)
            log_joint = log_joint + log_prob
    return log_joint
    
def ball_model():
    x = numpyro.sample("X", dist.Bernoulli(0.5))
    if x:  
        y = numpyro.sample("Y", dist.Bernoulli(2.0/3.0))
    else: 
        y = numpyro.sample("Y", dist.Bernoulli(1.0/4.0))
    return y
    
trace_model = trace(seed(ball_model, rng_seed=0)).get_trace()

cond_dict = {"X": jnp.array([1.]), "Y": jnp.array([1.])} # 袋a=1, 赤玉=1 
trace_model = trace(condition(seed(ball_model, rng_seed=0), cond_dict)).get_trace()

print(jnp.exp(log_prob_sum(trace_model)))

Array(0.3333333, dtype=float32)

block

blockハンドラを用いると、モデル内の指定された確率変数から隠蔽されます。これは例え以下のコードのようにconditionと組み合わせて条件付き確率を求めたい時に使うことができます。 https://pyro-book.data-hacker.net/docs/pyro_modeling/

cond_dict = {"X": jnp.array([1.]), "Y": jnp.array([1.])} # 袋a=1, 赤玉=1 
    
conditioned_model = condition(seed(ball_model, rng_seed=0), cond_dict)
blocked_model = block(conditioned_model, hide=["X"])
trace_model = trace(blocked_model).get_trace()

# xは隠されているのでtraceに残らない
print(trace_model.keys())
print(np.exp(log_prob_sum(trace_model)))

odict_keys(['Y'])
0.6666667

mask

maskを使用するとlog_probの値として０が返されることになります。欠測値を扱う際に使用されます。

d = dist.Normal(0, 1).expand([4]).mask(False)
samples = numpyro.sample("a", d, rng_key=random.PRNGKey(0))

print(samples)
print(d.log_prob(0))

[ 1.8160863  -0.75488514  0.33988908 -0.53483534]
[0. 0. 0. 0.]

詳しくは欠損値を扱う際に説明しますが、maskを使用することで以下のようなmodel2aとmodel2bが同じ結果になります。

x = np.ones(10)

def model2a(x):
    x_impute = numpyro.sample("x_impute", dist.Normal(0, 1).expand([4]))
    x_obs = numpyro.sample("x_obs", dist.Normal(0, 1).expand([6]), obs=x[4:])
    x_imputed = jnp.concatenate([x_impute, x_obs])
    
def model2b(x):
    x_impute = numpyro.sample("x_impute", dist.Normal(0, 1).expand([4]).mask(False))
    x_imputed = jnp.concatenate([x_impute, x[4:]])
    numpyro.sample("x", dist.Normal(0, 1).expand([10]), obs=x_imputed)

その他：配列操作

numpyの知識になりますが、ちょくちょく出てくる操作をメモとして残しておきます。

...（Ellipsisオブジェクト）

英語のellipsisは「省略」という意味なので、処理や引数を省略したい場合に使うものと考えられる。

array[..., None]

この場合Noneはnp.newaxisと同じ

numpy関数まとめサイト

以下のサイトでNumpyの基本操作がまとまっています。よくわからず使っているときに参考になります。

https://deepage.net/features/numpy/

最後に

以上で「NumPyro特有の関数などまとめ」は終わりです。次回以降はこれらの関数などを少しずつ使いながらモデリングをしていきます。