「経営学部のためのSaaSとサブスクリプションのデータ分析入門」の「SaaSの管理会計と経営データ分析」の章で平均継続期間(Average Duration)について紹介しました。
デュレーションと解約率変化に対するLTV変動率でもあります。
その関係式を導出します。
割引率r=0としたとき、解約率CCR、顧客あたり平均収益ARPAとすると、LTVは
LTV=\sum_{t=0}^{\infty} ARPA (1-CCR)^t
です。t=0のとき(1-CCR)^t=1なので、
\begin{align*}
LTV&=\sum_{t=0}^{\infty} ARPA (1-CCR)^t \\
&=ARPA + ARPA \sum_{t=1}^{\infty} (1-CCR)^t\\
\end{align*}
と初項を取り出します。LTVを解約率CCRで微分します。
\begin{align*}
\frac{\partial LTV}{\partial CCR}&=0+ ARPA \sum_{t=1}^{\infty} -t (1-CCR)^{t-1}\\
&=- ARPA \sum_{t=1}^{\infty} t (1-CCR)^{t-1}
\end{align*}
ここで、右辺に1=CCR/CCRを掛けます。
\frac{\partial LTV}{\partial CCR}=- \frac{ARPA}{CCR} CCR \sum_{t=1}^{\infty} t (1-CCR)^{t-1}
顧客生涯価値(LTV,CLV)の数式変形よりLTV=ARPA/CCRであり、サブスクリプションの平均継続期間(デュレーション)の数式変形より
AD=CCR \sum_{t=1}^{\infty} t (1-CCR)^{t-1}
なので、
\frac{\partial LTV}{\partial CCR}=- LTV \cdot AD
となります。両辺を-LTVで割ると
- \frac{1}{LTV} \frac{\partial LTV}{\partial CCR}= AD
となります。これはデュレーションが微小解約率変化に対する微小LTV変動率という意味になります。近似的に
- \frac{1}{LTV} \frac{\Delta LTV}{\Delta CCR} \simeq AD\\
であり、LTV変動率に関しての式に表すと、
\frac{\Delta LTV}{LTV} \simeq - AD \cdot \Delta CCR
となります。
実際に、解約率2%周りでの微小解約率変化に対するLTV変動率は、解約率が0.1%上昇し2.1%になるとLTVが5%下落するという計算になります。
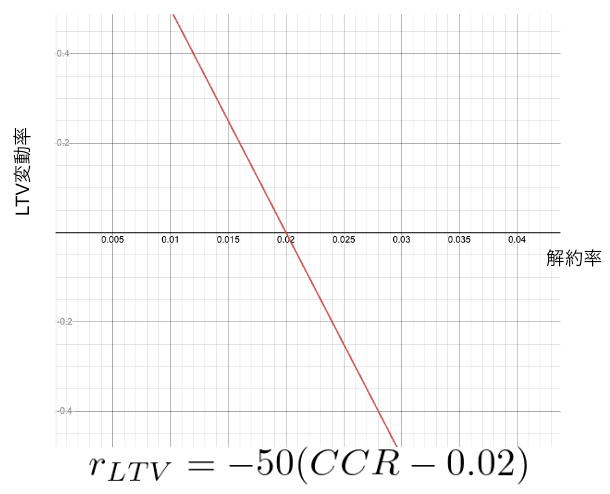

Discussion