機械学習による有効模型の構築とモンテカルロ法への応用
これは東京大学 物工/計数 Advent Calendar 2022のために書かれた記事です。
物理と機械学習のトピックとして、機械学習による有効模型の構築とそのモンテカルロ法への応用を紹介しようと思います。前者については、実装にも触れます。
導入: Gibbs-Bogoliubov-Feynman の不等式
物理では、解析が難しい模型の代わりに、自由度が小さく、エネルギースペクトルを部分的に説明する模型(有効模型)を扱いたいことがしばしばあります。
例えば、 Ising 模型において周囲のスピンからの寄与を平均化し、有効磁場からの影響と考え、一体問題として扱う近似(平均場近似)の結果得られる模型もその一種です。
そこで、「有効模型をどのように構築するか」という疑問が浮かびます。また、平均場近似がなぜ正当化されるかも気になります。
Gibbs-Bogoliubov-Feynman (GBF) の不等式はそれに対する 1 つの答えを与えてくれます。[1]
また、
で定義される変分自由エネルギー
ここで、
つまり、変分自由エネルギー、あるいは KL divergence を最小化することで有効模型を得ることができます。
(少なくとも Ising 模型における)平均場近似は変分原理の観点で正当化されるわけですね。

機械学習による有効模型の構築
Ising 模型の例はシンプルで、手計算で簡単に有効模型を求めることができました。
しかし、一般の複雑な模型では困難であることが想定されます。
そこで、計算機に乗せたくなります。
ところが、自由エネルギーを利用した変分法は計算量が大きいと考えられます。Ising 模型の例で言うと、最適な
今回は、Liu et al. (2016) や Fujita et al. (2017) を参考にして、機械学習による有効模型の構築手法について紹介します。
計算スキーム
厳密な Hamiltonian を
とします。ここで、
つまり、有効ハミルトニアンを求める問題は、最適な係数
学習データは固有状態
を利用します。
パラメータ
のように更新されます。連鎖律を使って示したように、誤差逆伝播法によって
Ising 模型では、
- 入力はスピンの状態
\{\sigma_n\} E_n - 学習データ
\{(x_i, y_i)\} x_i = \{\sigma_n\} y_i = \displaystyle{-J \sum_{\langle i, j \rangle} \sigma_i \sigma_j} - 試行 Hamiltonian を
\displaystyle{H_{\mathrm{trial}} = - \sum_i h_i \sigma_i} h_i
となります。
また、Fujita et al. (2017) では、Hubbard 模型に対して適用し、低エネルギーにおける有効模型としてスピン模型を学習されています。
実装
今回は、Liu et al. (2016) と同じ模型に対して適用してみます。
2 項目は同一セル内の 4 体スピン相互作用項です。
試行 Hamiltonian には、2 体スピン相互作用項のみを含む Ising 模型を仮定します。
今回は、3 次近接相互作用項まで取り入れてみます。
PyTorch を使って実装します。複数の系でコードを再利用するため、ベースとなるクラス BaseTrainer を作成します。
模型の詳細に依存する関数はクラス継承後作成するようにします。
import os
from typing import Callable, List, Tuple, Union
import torch
from torch.nn import MSELoss
from torch.optim import Optimizer
from torch.utils.data import DataLoader, TensorDataset
from torch.utils.tensorboard import SummaryWriter
from tqdm import tqdm
class BaseTrainer:
def __init__(self) -> None:
"""set basic constants of the system"""
pass
def effective_model(self, X: torch.Tensor, params: torch.Tensor) -> torch.Tensor:
"""effective hamiltonian
Args:
X (torch.Tensor): input data.
params (torch.Tensor): parameters.
Returns:
torch.Tensor: energy of effective hamiltonian. (number of data)
"""
raise NotImplementedError("This method should be overridden by derived class.")
def original_model(self, X: torch.Tensor) -> torch.Tensor:
"""original hamiltonian
Args:
X (torch.Tensor): input data.
Returns:
torch.Tensor: energy of original hamiltonian. (number of data)
"""
raise NotImplementedError("This method should be overridden by derived class.")
def sample_input(self, n_samples: int) -> torch.Tensor:
"""sample input data
Args:
n_samples (int): number of samples.
Returns:
torch.Tensor: input data.
"""
raise NotImplementedError("This method should be overridden by derived class.")
def init_params(self) -> torch.Tensor:
"""initialize parameters
Returns:
torch.Tensor: parameters.
"""
raise NotImplementedError("This method should be overridden by derived class.")
次に、BaseTrainer で模型に依らない部分を実装します。
まず、dataloader を作成します。バッチ処理が楽になります。
def create_dataloader(self, n_samples: int, batch_size: int) -> DataLoader:
"""create dataloader given samples and batch size
Args:
n_samples (int): number of data to sample.
batch_size (int): batch size
Returns:
DataLoader: dataloader for training or evaluation
"""
X = self.sample_input(n_samples)
Y = torch.FloatTensor(self.original_model(X))
ds = TensorDataset(X, Y)
dataloader = DataLoader(ds, batch_size=batch_size)
return dataloader
次に、学習や評価を実行する関数です。
loop は計算スキームで示した内容です。学習時は誤差逆伝播法で勾配を計算しパラメータを更新しています。
def loop(
self,
params: torch.Tensor,
dataloader: DataLoader,
loss_fn: Callable,
optimizer: Optimizer,
normalize_const: float = 1.0,
mode: str = "train",
) -> Union[float, Tuple[float, List[float], List[float]]]:
"""loop for training, evaluation and testing
Args:
params (torch.Tensor): params
dataloader (DataLoader): dataloader
loss_fn (Callable): loss function
optimizer (Optimizer): optimizer
normalize_const (float, optional): normalize constant for loss. Defaults to 1.0.
mode (str, optional): "train" or "eval". Defaults to "train".
Returns:
Union[float, Tuple[float, List[float], List[float]]]
loss when mode is "train" or "eval"
loss, original and effective hamiltonian when mode is "test"
"""
loss_sum = 0.0
E_original = []
E_eff = []
for X, Y in tqdm(dataloader, leave=False):
Y_eff = self.effective_model(X, params)
loss = loss_fn(Y / normalize_const, Y_eff / normalize_const)
if mode == "train":
optimizer.zero_grad()
loss.backward()
optimizer.step()
elif mode == "test":
E_eff += Y_eff.detach().tolist()
E_original += Y.detach().tolist()
loss_sum += loss.detach().item()
loss = loss_sum / len(dataloader)
if mode == "train" or mode == "eval":
return loss
elif mode == "test":
return loss, E_original, E_eff
以上をまとめて、__call__ メソッドを実装します。
当然のことですが、学習・評価・テストで異なるデータを利用しています。
また、損失関数には平均二乗誤差 (MSE) を使用し、 optimizer は SGD と Adam を選択できるようにしています。
学習のログは tensorboard で閲覧できるようにしています。
def __call__(
self,
output_dir: str,
lr: float = 0.001,
train_samples: int = 100,
eval_samples: int = 100,
test_samples: int = 100,
epochs: int = 3,
batch_size: int = 1,
optimizer_name: str = "Adam",
normalize_const: float = 1.0,
save_model=False,
) -> Tuple[List[float], List[float]]:
"""run optimization
Args:
output_dir (str): output directory.
lr (float, optional): learning rate. Defaults to 0.001.
train_samples (int, optional): number of training samples. Defaults to 100.
eval_samples (int, optional): number of evaluation samples. Defaults to 100.
test_samples (int, optional): number of test samples. Defaults to 100.
epochs (int, optional): number of training epochs. Defaults to 3.
batch_size (int, optional): batch size. Defaults to 1.
normalize_const (float, optional): normalize constant for loss. Defaults to 1.0.
optimizer_name (str, optional): optimizer name. "SGD" & "Adam" can be used. Defaults to "SGD".
Returns:
Tuple[List[float], List[float]]: energies of original and effective hamiltonian
"""
train_dataloader = self.create_dataloader(train_samples, batch_size)
eval_dataloader = self.create_dataloader(eval_samples, 1)
test_dataloader = self.create_dataloader(test_samples, 1)
params = self.init_params()
loss_fn = MSELoss()
if optimizer_name == "Adam":
optimizer = torch.optim.Adam([params], lr=lr)
elif optimizer_name == "SGD":
optimizer = torch.optim.SGD([params], lr=lr)
else:
raise NotImplementedError
writer = SummaryWriter(log_dir=os.path.join(output_dir, "logs"))
with tqdm(range(epochs)) as pbar_epoch:
for epoch in range(epochs):
pbar_epoch.set_description("[Epoch %d]" % (epoch + 1))
loss = self.loop(
params,
train_dataloader,
loss_fn,
optimizer,
normalize_const,
mode="train",
)
writer.add_scalar("train loss", loss, epoch)
tqdm.write(f"train loss at epoch{epoch+1}: {loss}")
with torch.no_grad():
loss = self.loop(
params,
eval_dataloader,
loss_fn,
optimizer,
normalize_const,
mode="eval",
)
writer.add_scalar("eval loss", loss, epoch)
tqdm.write(f"eval loss at epoch{epoch+1}: {loss}")
with torch.no_grad():
loss, E_original, E_eff = self.loop(
params,
test_dataloader,
loss_fn,
optimizer,
normalize_const,
mode="test",
)
tqdm.write(f"test loss: {loss}")
if save_model:
torch.save(params, os.path.join(output_dir, "model.pth"))
return E_original, E_eff
BaseTrainer を継承して、今回適用する系のクラスを実装します。
模型やデータサンプル、パラメータの初期化を追加実装しています。(模型の実装が汚いのが心残りですが...)
ここで、X[:, (i + 1) % Lx, j] などのようにして周期的境界条件を反映しています。
class Spin4InteractionTrainer(BaseTrainer):
def __init__(self, J, K, Lx, Ly) -> None:
"""set basic constants of the system
Args:
J (float): coefficient of 2 spin interaction.
K (float): coefficient of 4 spin interaction.
Lx (int): lattice size of dimension x.
Ly (int): lattice size of dimension x.
"""
self.J = J
self.K = K
self.Lx = Lx
self.Ly = Ly
def effective_model(self, X: torch.Tensor, params: torch.Tensor) -> torch.Tensor:
"""effective model
Args:
X (torch.Tensor): spin. (number of data, lattice size x, lattice size y)
params (torch.Tensor): parameters. (number of parameters)
Returns:
torch.Tensor: energy of effective Hamiltonian. (number of data)
"""
batch_size = X.shape[0]
max_n = params.shape[0]
interact = torch.zeros((batch_size, max_n - 1))
for i in range(self.Lx):
for j in range(self.Ly):
interact -= torch.stack(
[
self.neighbor_interact(n, X, i, j, self.Lx, self.Ly)
for n in range(1, max_n)
],
dim=1,
)
interact /= 2 # 2 is for double counting
interact = torch.concat((torch.ones((batch_size, 1)), interact), dim=1)
H = torch.einsum("bx,x->b", interact, params)
return H
def original_model(self, X: torch.Tensor) -> torch.Tensor:
"""original Hamiltonian
Args:
X (torch.Tensor): spin. (number of data, lattice size x, lattice size y)
Returns:
torch.Tensor: energy of original Hamiltonian. (number of data)
"""
n_data, Lx, Ly = X.shape
H = torch.zeros(n_data)
for i in range(Lx):
for j in range(Ly):
H += (
-self.J * self.neighbor_interact(1, X, i, j, self.Lx, self.Ly) / 2
- self.K * self.interact_cell(X, i, j, self.Lx, self.Ly) / 4
)
return H
def neighbor_interact(
self, n: int, X: torch.Tensor, i: int, j: int, Lx: int, Ly: int
) -> torch.Tensor:
"""calculate interaction with neighbors
Args:
n (int): n th neighbor
X (torch.Tensor): spin. (number of data, lattice size x, lattice size y)
i (int): index of position x.
j (int): index of position y.
Lx (int): lattice size of dimension x.
Ly (int): lattice size of dimension y.
Returns:
torch.Tensor: interaction with neighbors. (number of data)
"""
if n != 2:
return X[:, i, j] * (
X[:, (i + n) % Lx, j]
+ X[:, (i - n) % Lx, j]
+ X[:, i, (j + n) % Ly]
+ X[:, i, (j - n) % Ly]
)
elif n == 2:
return X[:, i, j] * (
X[:, (i + 1) % Lx, (j + 1) % Ly]
+ X[:, (i + 1) % Lx, (j - 1) % Ly]
+ X[:, (i - 1) % Lx, (j + 1) % Ly]
+ X[:, (i - 1) % Lx, (j - 1) % Ly]
)
else:
NotImplementedError
def interact_cell(
self, X: torch.Tensor, i: int, j: int, Lx: int, Ly: int
) -> torch.Tensor:
"""calculate interaction in a cell
Args:
X (torch.Tensor): spin. (number of data, lattice size x, lattice size y)
i (int): index of position x.
j (int): index of position y.
Lx (int): lattice size of dimension x.
Ly (int): lattice size of dimension y.
Returns:
torch.Tensor: interaction with neighbors. (number of data)
"""
return X[:, i, j] * (
X[:, (i + 1) % Lx, j]
* X[:, i, (j + 1) % Ly]
* X[:, (i + 1) % Lx, (j + 1) % Ly]
+ X[:, (i - 1) % Lx, j]
* X[:, i, (j + 1) % Ly]
* X[:, (i - 1) % Lx, (j + 1) % Ly]
+ X[:, (i + 1) % Lx, j]
* X[:, i, (j - 1) % Ly]
* X[:, (i + 1) % Lx, (j - 1) % Ly]
+ X[:, (i - 1) % Lx, j]
* X[:, i, (j - 1) % Ly]
* X[:, (i - 1) % Lx, (j - 1) % Ly]
)
def sample_input(self, n_samples):
X = 1 - 2 * (torch.rand(n_samples, self.Lx, self.Ly) < 0.5)
return X.float()
def init_params(self):
h = torch.ones(4, dtype=torch.float32, requires_grad=True)
return h
まとめると以下のようになります。
実験結果
30×30 の格子に対して適用した結果を示します。
学習は 1000 サンプルを使用してバッチサイズ 1 で 10 エポック行い、厳密な系のパラメータは
学習時、評価時ともに十分誤差が小さいことが分かります。
なお、Liu et al. (2016) の記述から推察し、誤差を系のサイズで規格化することによって誤差のオーダーを著者の結果と合わせているため見かけ上は非常に小さい誤差になっています。
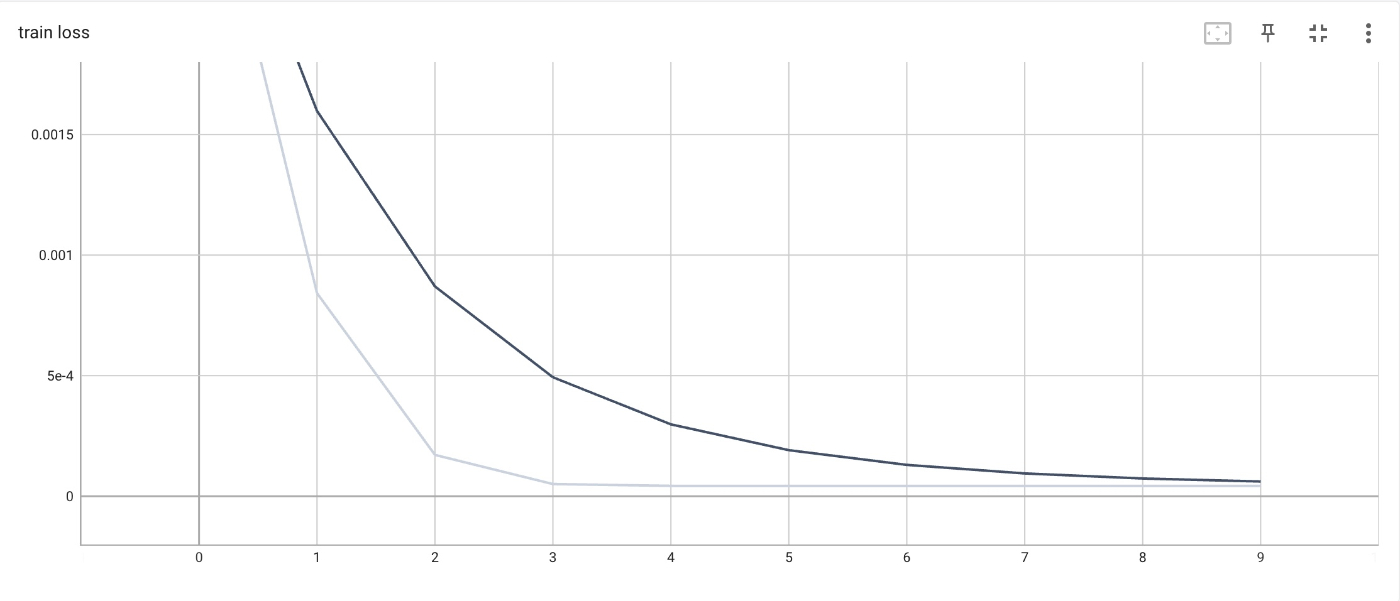
学習時の損失関数。系のサイズで規格化。
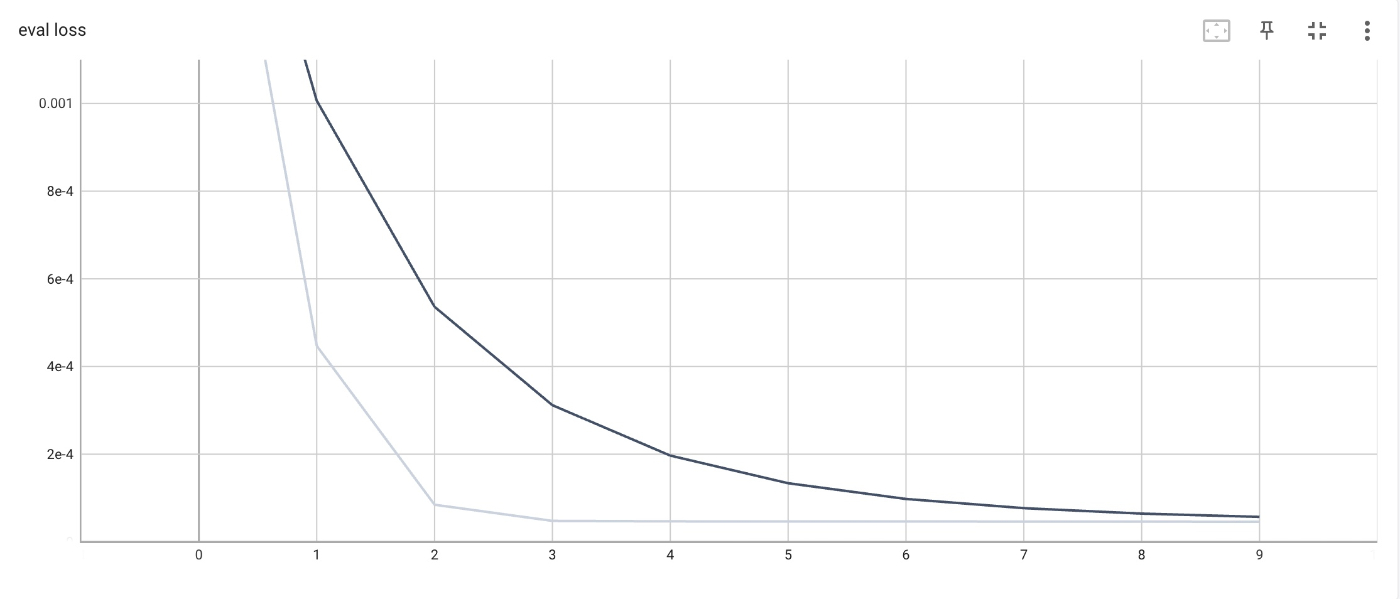
評価時の損失関数。系のサイズで規格化。
次に、厳密な模型と学習した有効模型のエネルギーを比較します。この図からも、十分に学習できていることが分かります。
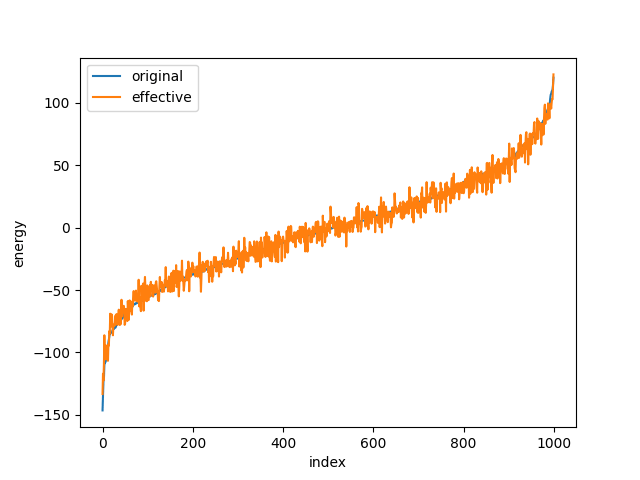
厳密な模型と学習した有効模型のエネルギーの比較。
厳密な模型のエネルギーでインデックスをソート。
また、学習されたパラメータは以下のようになりました。スピン間の距離が近いほど寄与が強いことが分かります。
自己学習モンテカルロ法 (self-learning Monte-Carlo method)
機械学習を用いて有効 Hamiltonian を構築する方法を紹介しました。
次に、その応用先として自己学習モンテカルロ法 (Liu et al., 2016) を紹介します。
モチベーション
モンテカルロ法では、マルコフ過程に従うように状態遷移します。そのための条件として、詳細釣り合い条件
状態の更新方法は大きく 2 つに分けられます。
- 局所的更新 (local update)
- ランダムに選んだ 1 サイトの変数を変えることで、次の状態を提案し、その状態に移るかどうかを詳細釣り合い条件に従って決定
- 模型に依存せず汎用的に使える
- 一方、相転移点付近では鈍化することが知られている
- 大域的更新 (global update)
- 多数のサイトの変数が絡むような更新を行う
- 模型の詳細に依るため汎用性が低く、効率的なアルゴリズムが見つかっている模型は少ない
提案手法
まず、厳密な Hamiltonian に基づく局所的更新によって学習データを生成します。あるいは、元の Hamiltonian が既知であることが多いので、前章で示した方法によって学習データは自動生成することができます。
次に、効率的な大域的更新方法が知られている試行ハミルトニアンを仮定してパラメータを学習し、有効模型を構築します。
その有効模型に対する大域的更新方法に従って次の配位を提案し、元の Hamiltonian に基づく詳細釣り合い条件から採択するか棄却するかを判断します。
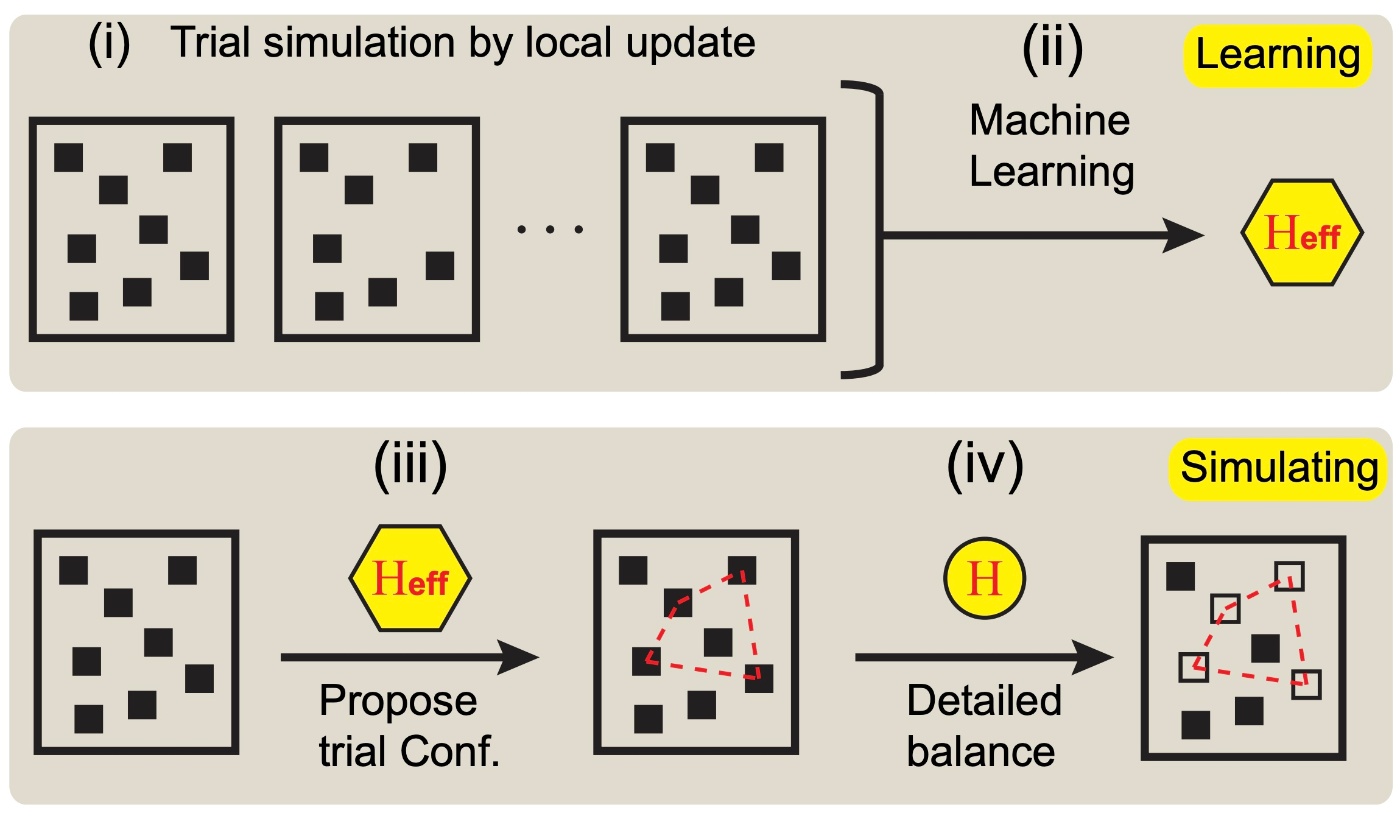
自己学習モンテカルロ法のフレームワーク。Liu et al. (2016) より引用。
(i) 厳密な Hamiltonian に基づく Monte Carlo 法によって学習データを生成。
(ii) 効率的な大域的更新方法が知られている有効模型を構築。
(iii) 有効模型に対する大域的更新方法に従って配位を提案。
(iv) 元の Hamiltonian に基づく詳細釣り合い条件から採択・棄却を決定。
実装
Ising 模型に対する大域的なアルゴリズムとして、Wolff のアルゴリズムが知られています。一方、有効模型の学習の章で扱った 4 スピン相互作用が入った模型に対しては、効率的な大域的更新方法が知られていません。つまり、有効模型を学習し、Wolff のアルゴリズムを適用することでシミュレーションを高速化できると考えられます。
当初はこちらも実装するつもりでしたが、既にコンテンツ量が多くなってしまったので、気が向いたら実装についても書いてみることにします。[2]
実験結果 (Liu et al., 2016)
折角なので、著者の実験結果を示します。模型は有効模型の学習で使用したものと同じです。
臨界温度における自己相関関数の時間変化を表していて、この減衰が速い(自己相関時間が短い)ほどモンテカルロ法が高速であることを示しています。
厳密な模型に Wolff のアルゴリズムを適用してもあまり改善しませんが、自己学習モンテカルロ法により減衰が速くなっています。

局所的更新、自己学習モンテカルロ法、Wolff のアルゴリズムでの自己相関関数の減衰。
Liu et al. (2016) より引用。
さいごに
物理 × 機械学習の一例として、有効模型の構築と自己学習モンテカルロ法を扱ってみました。
実装や発想はシンプルながら適用範囲の広い手法で、実験し甲斐がありそうです。
自己学習モンテカルロ法は、コンテンツ量と工数の都合上、実装を紹介できませんでしたが、いつか書いてみようと思います。
参考文献
[1] Fujita, H., Nakagawa, Y. O., Sugiura, S., & Oshikawa, M. (2018). Construction of Hamiltonians by supervised learning of energy and entanglement spectra. Physical Review B, 97(7), 075114.
[2] Liu, J., Qi, Y., Meng, Z. Y., & Fu, L. (2017). Self-learning monte carlo method. Physical Review B, 95(4), 041101.
[3] Naoki, K. (2019). Lecture 2: Meanfield approximation, variational principle and Landau expansion. 物工の演習では変分自由エネルギーと自由エネルギーの差が非負であることは示しますが、その差が KL divergence になることはこちらの資料を参考にしました。
余談
Hamiltonian を学習する文脈で、Hamiltonian Neural Network (Greydanus, 2019) というものがあります。これは、古典力学系において、観測データを入力、正準方程式の残差を損失関数としてニューラルネットワークを学習することにより、Hamiltonian を推定する手法です。元々はこれを実装するつもりでしたが、著者実装が公開されている上にそれがあまりにもリッチだったのでやめました。
量子系でも同様のことができないかぼんやり考えています。
Zenn で執筆するのは初めてでしたが、Github 連携と VSCode 拡張 (Zenn Editor) が便利でした。以下の記事を参考にしました。
Discussion