【AHC参加記】AHC038で、貪欲法と畳み込みを実践してみた
10/31追記
延長戦の感想記事もできました!
はじめに
2024-10-04(金) ~ 2024-10-14(月) に開催されていたプログラミングコンテストである、
トヨタ自動車プログラミングコンテスト2024#10(AtCoder Heuristic Contest 038)に参加して入茶できたため、思考過程の記録も兼ねて、参加記を残します。
今までAHCには2回参加しましたが、ほぼサンプルコードコピペ+微改善だけだったため、数日間しっかり参加したのは今回が初です。
AtCoder Heuristic Contest (AHC)とは
オンライン上で不定期に(約1ヶ月に1回)開催されている、AtCoder社が主催するプログラミングコンテストの一つです。
公式の『AtCoder Heuristic Contest(AHC)とは?』より一部抜粋。
AtCoderにて新たに定期的に開催されるプログラミングコンテストです。ABC/ARC/AGCなどのアルゴリズムコンテストと異なり、最適解を出すのが難しい問題に対し、出来るだけ良い解を作成するコンテストとなります。
レーティングが 単調非減少型 であり、プレッシャーなく楽しめるのもおすすめポイントです。
AHC038 問題文
問題文はこちら。
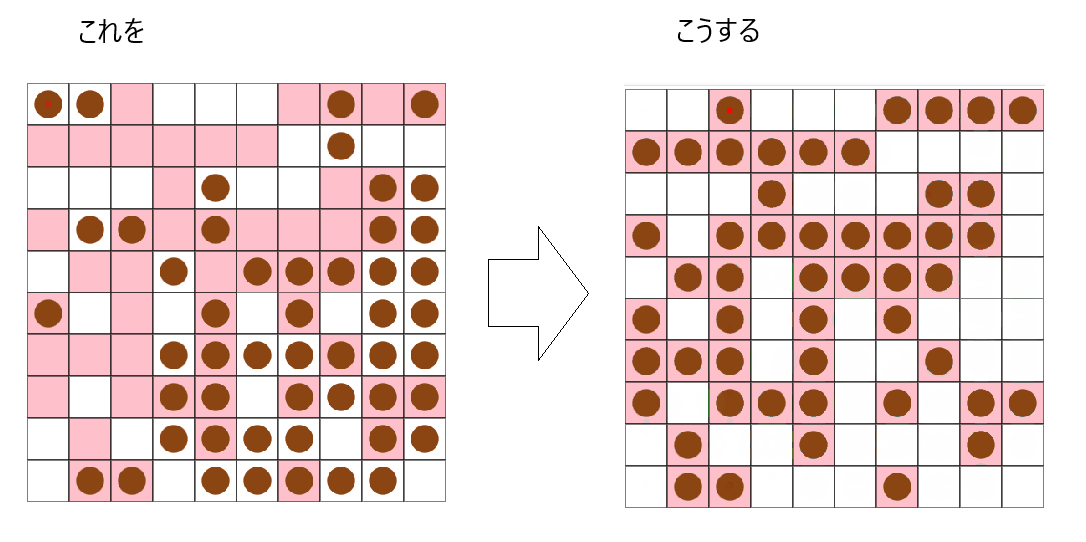
「ランダムに散らばったたこ焼きを、できるだけ素早く目的地に並べる」ことが要求されていそうです。
try 1: とにかく通す
サンプルは木がガクガク変形していて地獄か?と思ったため、ひとまず「とにかく通す」路線で行きます。以下、「目的地にいないたこ焼き」を「要移動たこ焼き」と呼ぶことにします。
一番単純に、 アームの頂点数を1に固定 します。「要移動たこ焼き」をピックして、一番近い目的地に移動させてリリースする、を繰り返せば通るはずです。
アーム初期座標 = (0, 0)
queue = 「要移動たこ焼き」の座標すべて
while (queueが空でない) {
[ピック座標] = queueからポップ
[ピック座標]にアームを移動
ピック
[リリース座標] = 一番近いゴールの座標
[リリース座標]にアームを移動
リリース
}
Webのビジュアライザも初使用しました。とても便利。 inputとoutputだけ貼ればよいことに気付くのに数分かかりました
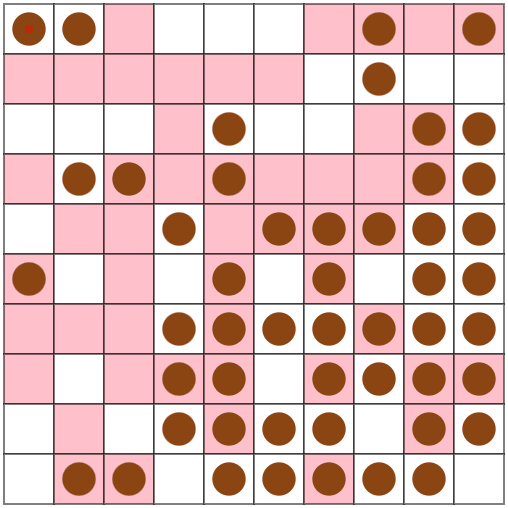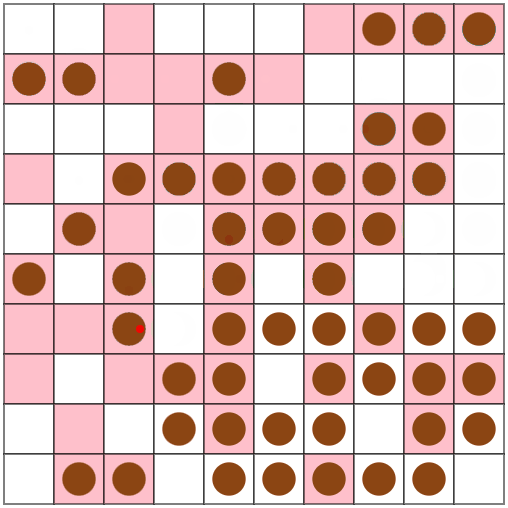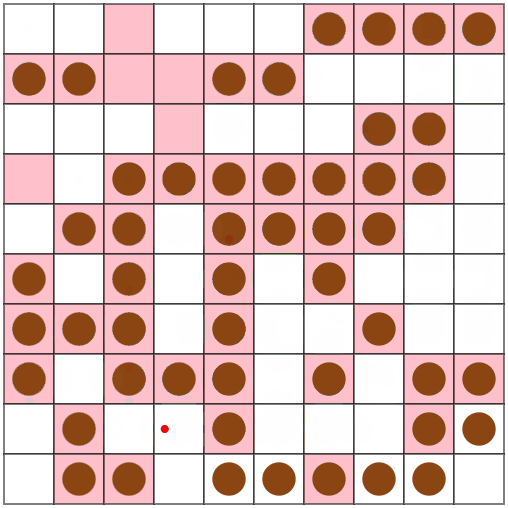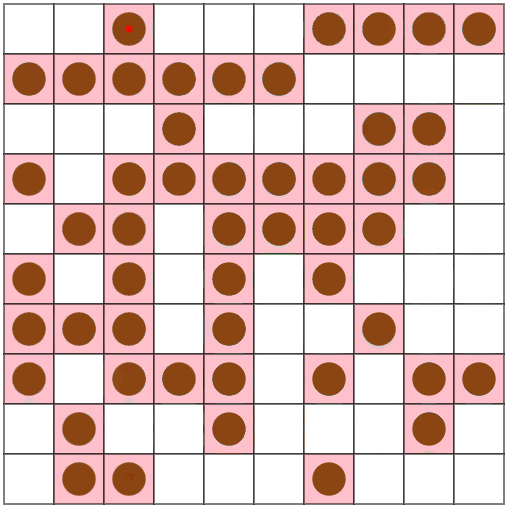
ひとまず
try 2: より貪欲に
いくつかseedを変えながらビジュアライザを見ていると、アーム初期座標が(0, 0)だと「要移動たこ焼き」への移動に時間がかかる場合があったり、リリース後に遠くの「要移動たこ焼き」をピックしに行ってしまったりしていることが分かりました。
そこで、アーム初期座標を「要移動たこ焼き」の座標にするとともに、次にピックする「要移動たこ焼き」も貪欲に探索することにしました。ついでに、移動とピック&リリースは同時にできることに気付いたため、それも合わせて修正しました。
アーム初期座標 = いずれかの「要移動たこ焼き」の座標
while (「要移動たこ焼き」が存在する) {
[ピック座標] = 一番近い「要移動たこ焼き」の座標
[ピック座標]にアームを移動しながら、同時にピック
[リリース座標] = 一番近いゴールの座標
[リリース座標]にアームを移動しながら、同時にリリース
}
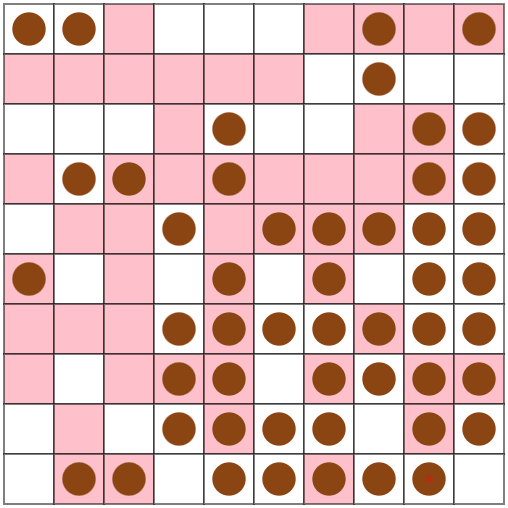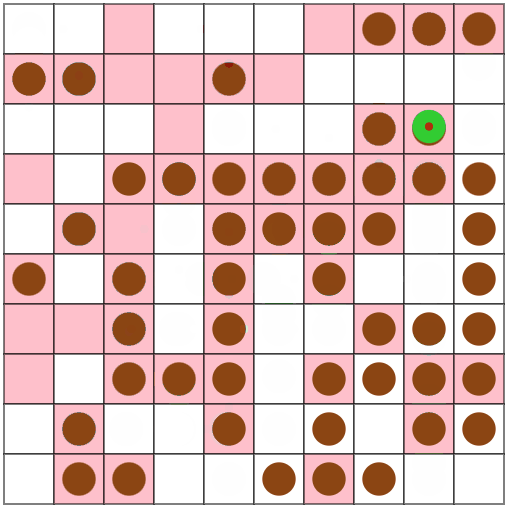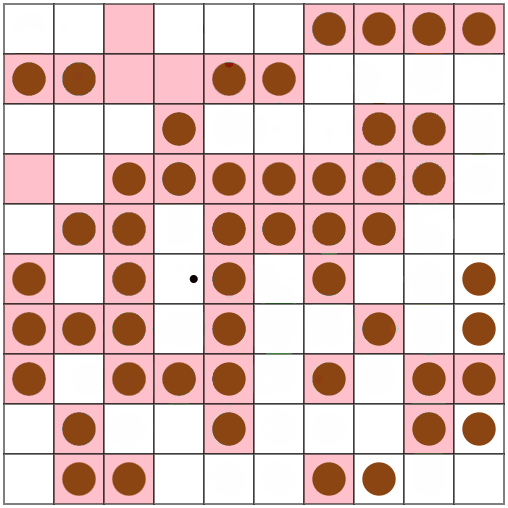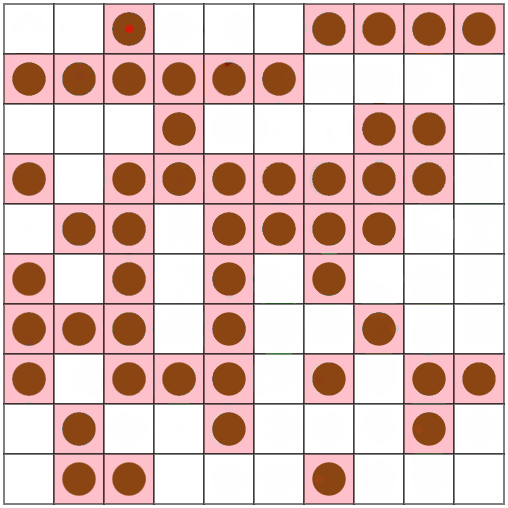
スコアが15%ほど改善しました。楽しい。
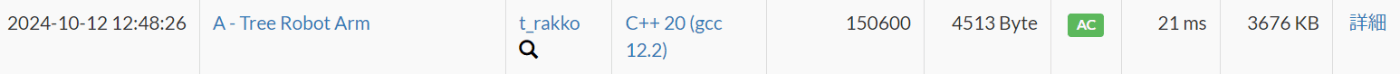
try 3: 複数まとめて運びたい
1頂点アームでACは取れましたが、やはり複数頂点のアームを使ってまとめてピック&リリースするのが効率が良さそうです。
サンプルのように木がガクガク変形すると私の現時点の実力では処理しきれなさそうなので、 横一列にアームの形を固定し、回転は全頂点180度回転に限定する という制約をつけてみることにします。これなら、平行移動しても回転しても処理しやすそうです。
[ピック座標]を貪欲に探索する場合、1頂点であれば一番近い「要移動たこ焼き」の座標で良いですが、複数頂点の場合には「近さ」と「まとめて運ぶこと」のバランスを取る必要があります。
そこで、以下の[総合スコア]という値を畳み込みを使って計算し、これを最小化することを考えてみます。
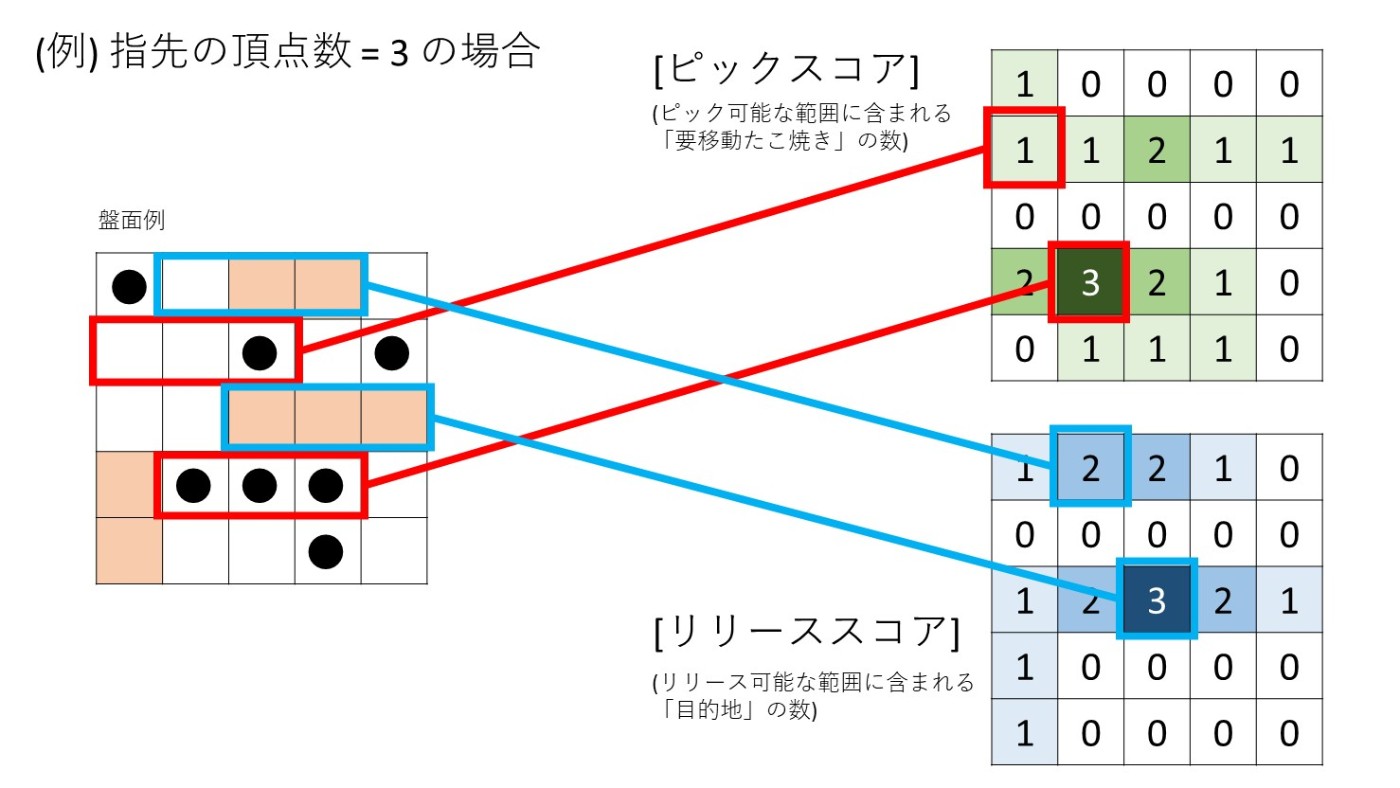
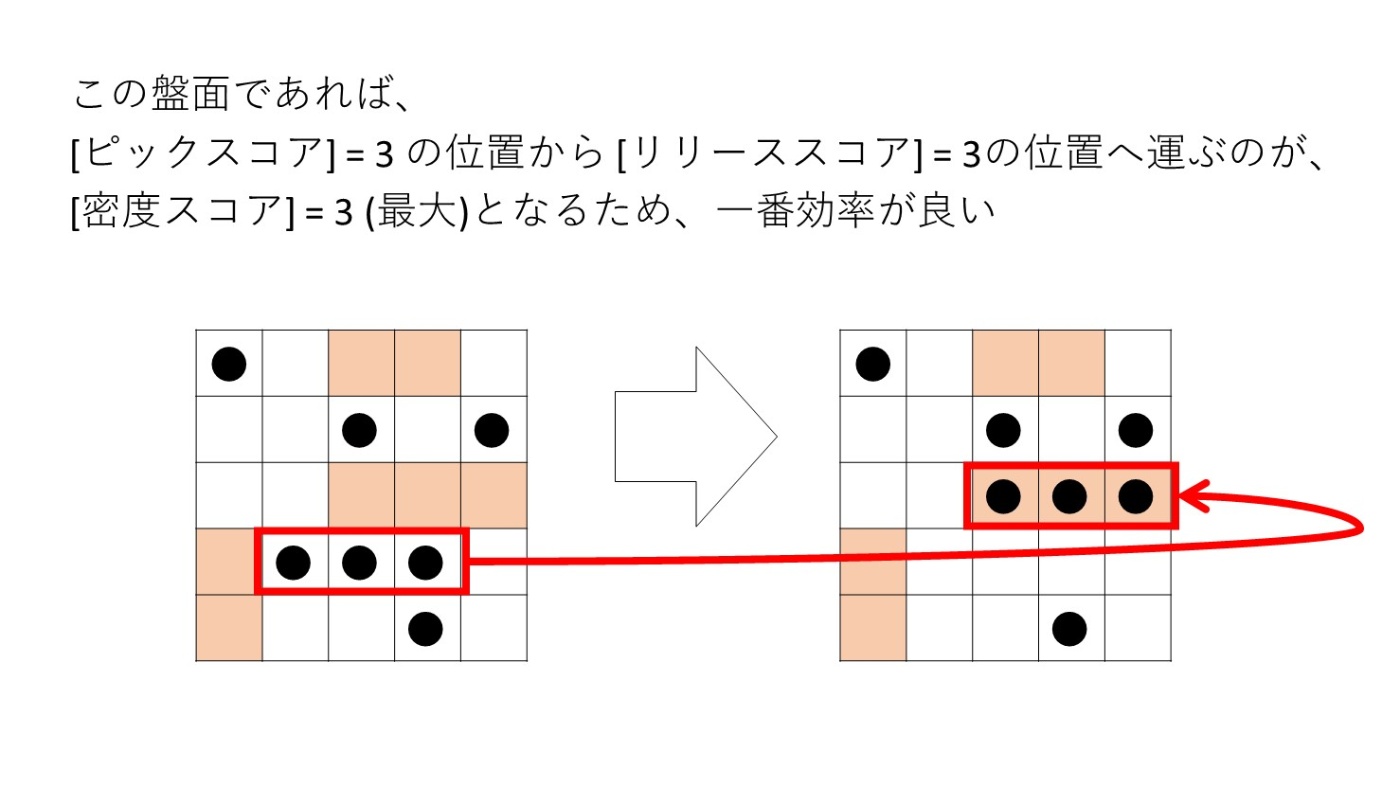
[密度スコア]については、アームの頂点数が1の場合は[密度スコア]は常に1になるため、[密度スコア]が1より大きい場合、「まとめて運ぶと、頂点数1の場合より効率的に運べる」ことが分かります。
[総合スコア]は、アームの移動距離も考慮したスコアです。[密度スコア]を分母に持ってくることで、「少し遠くても、まとめて運ぶ方が良さそうであれば、遠くのものをまとめて運ぶことを優先する」ように設計しました。
この[総合スコア]を毎ターンの初めに計算し、[総合スコア]が最小になるような[ピック範囲]と[リリース範囲]、およびアームの頂点数を選べば、「近さ」と「まとめて運ぶこと」のバランスを取りつつ貪欲に探索できそうです。
フィールド全体×フィールド全体×アームの頂点数の計算を毎ターン行うことになるので計算量が心配ですが、フィールドの大きさはN ≦ 30なので適用可能と思われます。
ピック範囲とリリース範囲を決定する関数 () {
フィールド全体×フィールド全体×アームの頂点数について[総合スコア]を計算する
[総合スコア]を最小化する[ピック範囲]と[リリース範囲]を求める
}
ピック座標とリリース座標を決定する関数 () {
[ピック座標] = [ピック範囲]の真横とする
[リリース座標] = [リリース範囲]の真横とする
}
移動・ピック・移動・リリースを実行する関数 () {
[ピック座標]にアームを移動しながら、同時にピック
[リリース座標]にアームを移動しながら、同時にリリース
}
初期位置 = いずれかの「要移動たこ焼き」の座標
while (「要移動たこ焼き」が存在する) {
ピック範囲とリリース範囲を決定する関数 ()
ピック座標とリリース座標を決定する関数 ()
移動・ピック・移動・リリースを実行する関数 ()
}
実行してみました。

スコアは約2.5分の1に減少しました。平均的に2.5個のたこ焼きを同時に運べていそうです。楽しい。
try 4: 根本以外でのピックを可能にする
上記のtry 3のビジュアライザを見ると、後半に入って、1個しかピックできなくなってからが長いです。よく見ると、アームの根元でたこ焼きを迎えに行っています。
これはtry 3の「ピック座標とリリース座標を決定する関数」で、[ピック座標]を[ピック範囲]の真横と決め打ちしていたためです。
そこで、現在位置から一番移動距離が少なくなるような[ピック座標]を探索する処理を追加しました。
ピック座標とリリース座標を決定する関数 () {
[ピック座標] = [ピック範囲]を包含できるアームの座標のうち、現在座標から一番近い点
[リリース座標] = [リリース範囲]と[ピック座標]から決まる点
}
その結果、アームの根元以外でのピック・リリースが可能になりました。
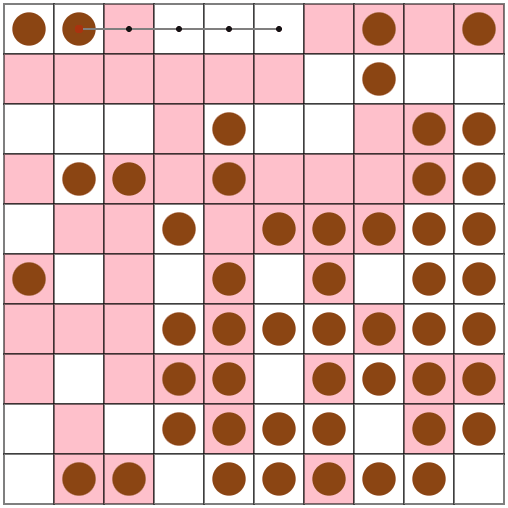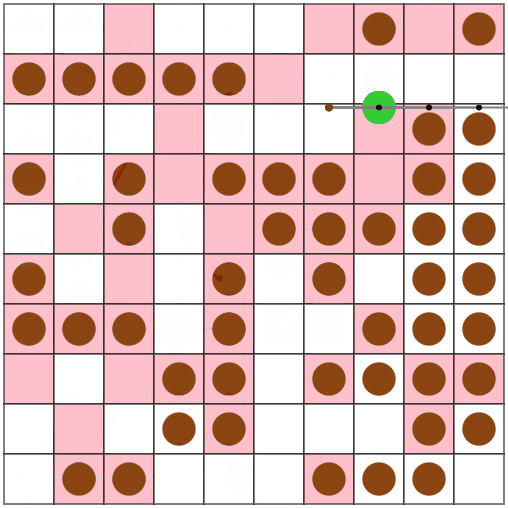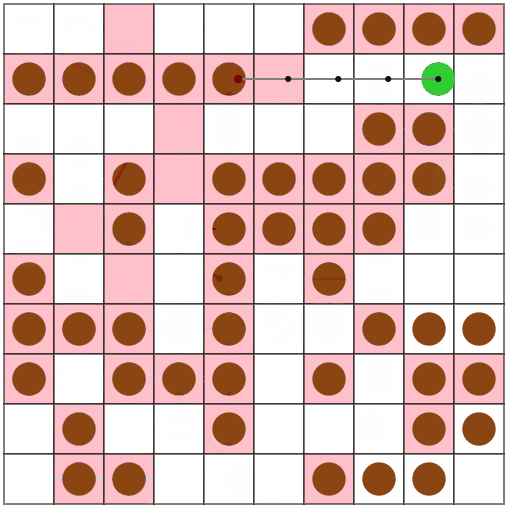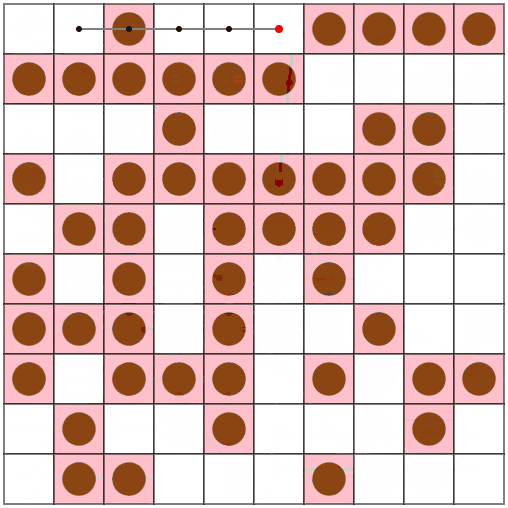
スコアも25%ほど改善しました。楽しい。
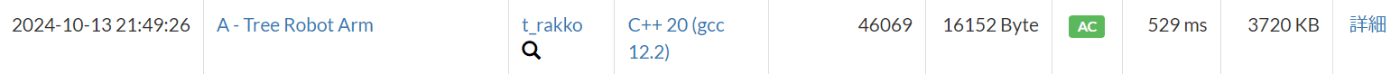
最終結果
アーム横一列縛りの条件下ではある程度目途がついたと考えたため、上記のtry 4で最終提出としました。ソースコードはこちら ⇒ ソースコード
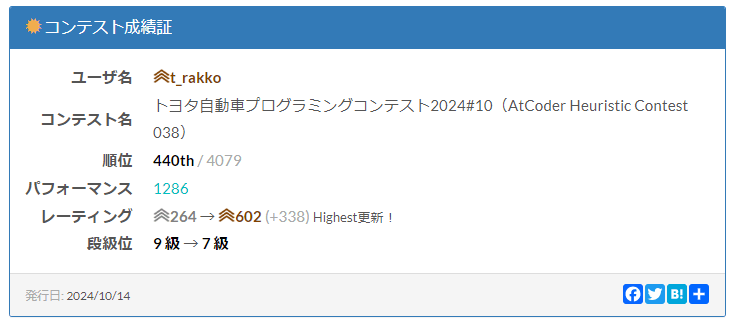
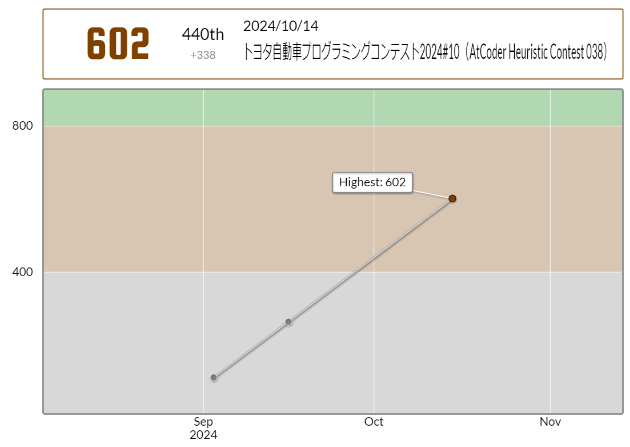
最終440位(参加登録は4079人、正答者は798人)で、パフォーマンスは1286。3回目の参加にして入茶することができました!!
(横一列固定変形無しという制約下のなかでは)そこそこ良いスコアを出せたのではないでしょうか。
感想
AHCにしっかり時間を取って参加したのは今回が初めてでしたが、控えめに言って最高でした。
自分でアイデアを出して実装し、その結果スコアを改善していくのを見るのはとても楽しかったです。
また、プレッシャーにさらされるとすぐにダウンしがちな私としては、レートが単調非減少で、あまり根を詰めずに気楽に取り組めるのがとてもありがたいです。
他にも、プログラムがある程度長くなり、かつ何度も改善していく必要があるため、必然的に保守性を考慮したクラス・関数設計をせざるを得ない ≒ そういうシステム設計の練習にもなる、という点でも、ABCとは異なった観点での実力UPに繋がりそうです。
総じてとてもおすすめなので、まだAHC参加したことが無い方もぜひ参加してみましょう!
また、もしAHC038参加された方でこの記事を読んでいらっしゃる方がいたら、なにとぞ、参加記を書いてください!!!!お願いします!!!!
他の方の解説記事や参加記など、とても楽しく拝見&参考にさせていただいております。知らないことばかりでとても勉強になります。
これにて本記事は終了です。ここまで読んでくださりありがとうございました!
お勉強 (自分用)
TwitterでAHC038を検索すると、いろいろな言葉が流れてきます。ABCと比べて「○○法を知らないから手も足も出ない」ということは少なそうですが、あまりに言葉を知らないのもどうかと思ったのでお勉強します。。。
ビームサーチ
最大のスコア1個のみを追求するのではなく、スコア上位の複数の解候補を残しつつ探索していくことで、大域最適につなげやすくする探索手法。
つまり、、、高級な貪欲法?
焼きなまし
こちらのページがとても参考になったため、リンクを張らせていただきます m(_ _)m
最大のスコアのみを追求するのではなく、特に序盤の内は悪いスコアへの遷移も許容することで、大域最適に繋げやすくする探索手法。
つまり、、、高級な貪欲法?
鉄則本など調べて実装してみたいと思います。
Discussion