🍪

AHC038延長戦で「16-8-4-2-1アーム」を使う

2024/10/31に公開

 はじめに前回の記事にて、2024-10-04(金) ~ 2024-10-14(月) に開催されていたプログラミングコンテストである「AHC038」の参加記を書きましたが、その後1週間ほど経ってから、「AHCラジオ」という公式解説の存在に気付きました。

https://www.youtube.com/live/lJWAnmZWWSw
その中で「16-8-4-2-1アーム」という考えが触れられており、実際に自分で実装してみたくなったため、延長戦ということで実装してみました。以下、その内容についてまとめていきます。

 参考記事188位の方の参加記です。図解もありとても分かりやすかったです。

https://vvani07.hatenadiary.org/entry/2024/10/17/003748

 実現したいこと上記記事のすすめに従って、「16-8-4-2-1アーム」を実装する。
ただし上記記事の最後には『N>=18 で V=5 のケースはけっこう厳しい』との注意書きがある。そこで、 このケースにも対応できるように、根の平行移動にも対応する 。

 設計
 多関節ロボットアームとして考えてみるたこ焼きのピック＆リリースに使える指先が1頂点で、それ以外の回転する剛体が複数連結していることから、多関節ロボットアームの動作計画問題と同じ流れを使ってみると、考え方のベースとして良さそうです。
こういうやつ。

多関節ロボットアームについては↓の記事が参考になった...気がします。

https://qiita.com/sekky0816/items/6bcea810de99449b4cbc

https://jp.mathworks.com/discovery/inverse-kinematics.html
以後、たこ焼きをピック＆リリースする指先頂点を 「エンドエフェクタ」 、ロボットの根に相当する頂点を 「ルート」 、回転する剛体部分を 「リンク」 と呼ぶことにします。

 0. 詳細設計まず、たこ焼きを1つピック＆リリースする際の流れとして、以下のような手順を考えました。
エンドエフェクタの目標座標(targetEndPos)を決める
targetEndPosを実現できるような、ルートの目標座標(targetRootPos)と、各リンクの目標角度(targetOrientation)を計算する
現時点でのルートの座標・各リンクの角度から、targetRootPos・targetOrientationを実現するための経路を生成する
生成した経路に従ってロボットを動かし、たこ焼きをピック＆リリースする

 1. targetEndPosを決める今回の「16-8-4-2-1」アームは、アームのカバー範囲内であれば、どのマスにも最悪2ターンでアクセスできるのが特徴です。
そこで、ターゲットを選ぶ際には、まずアームのカバー範囲内にあるたこ焼きを優先し、もし仮にカバー範囲内に1つもたこ焼きがなければ、現在のルート座標とのマンハッタン距離が一番近いものを選ぶようにすれば良さそうです。

 2. targetRootPosとtargetOrientationを計算する続いて、「エンドエフェクタをtargetEndPosに持ってくるためには、ルートはどの座標にいて、各リンクの回転角度はどのくらいであるべきか？」という問題を解く必要があります。

ロボティクス界隈では「逆運動学」と呼ばれる問題で、とても解くのが難しいです。
困っていたところ、前述の参考記事にとても有益な記述を見つけたため、参考にさせていただきました。ありがとうございます！！
アームの向きによって指先がどの座標に行くのか？は愚直にシミュレーションをすればわかるので、事前にやって変換テーブルを作っておくと良いでしょう。
天才か？
事前に、「各リンクの回転角」を全パターン(リンクが5本なら pow(4,5) = 1024通り)試し、それぞれのパターンにおける「エンドエフェクタの座標とルートの座標の差分」を計算し、std::mapに「エンドエフェクタの座標とルートの座標の差分」⇒「各リンクの回転角」を記録しておきます。
これにより、targetRootPosさえ決めてしまえば、逆運動学の計算をせずとも簡単にtargetOrientationが引き出せるようになりました。
targetRootPosはNが小さいので全探索し、現時点のルート座標・回転角から考えて一番到達しやすい点を選べばよいでしょう。

 3. 経路を生成するtargetRootPosとtargetOrientationが確定したら、現時点のルート座標・回転角からそこに到達するための経路を生成します。
needTurn = max(平行移動に必要なターン数, 回転に必要なターン数, ピック＆リリースに必要なターン数(1)) として、vector<string>(needTurn)を最初に確保し、適宜必要な移動を割り付けていくことにしました。

 4. ロボットを動かす後は、生成した経路に従ってロボットを動かし、エンドエフェクタがtargetEndPosに来たら、たこ焼きをピック＆リリースするだけです。

 プログラム上記をまとめると、以下のようなプログラムになりました。
struct RobotInfo {
    現在のルート座標
    現在のリンク角度
    [座標の差 ⇒ リンク角度 変換map]
    RobotInfo() {
        [座標の差 ⇒ リンク角度 変換map]を作る
    }
}

targetEndPosを決める関数() {
    アームのカバー範囲内にターゲットが有るならそれを選択。
    無ければ、マンハッタン距離が最小のものを選択。
}

targetRootPosとtargetOrientationを計算する関数() {
    [座標の差 ⇒ リンク角度 変換map]を使い、targetRootPosとtargetOrientationを求める。
}

経路を生成する関数() {
    必要なターン数(needTurn)を求める。
    vector<string>(needTurn)を確保し、適切な操作列を割り当てる。
}

ロボットを動かす関数(){
    生成した経路に従ってロボットを動かす。
    targetEndPosに存在するたこ焼き・ゴールをsetから消す。
}

int main () {
    ロボットを定義(RobotInfoインスタンスを生成)する。
    set = 要移動たこ焼き, 要充填ゴール

    while (setが空でない) {
        targetEndPosを決める関数()
        targetRootPosとtargetOrientationを計算する関数()
        経路を生成する関数()
        ロボットを動かす関数()
    }
}
https://atcoder.jp/contests/ahc038/submissions/59291562

 結果前回記事でのプログラム(本番440位)と比べて、スコアが2倍以上になり、延長戦順位で340位に上がりました！

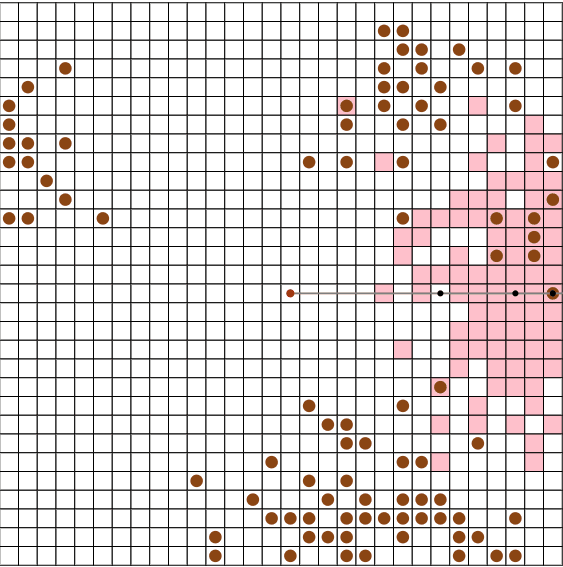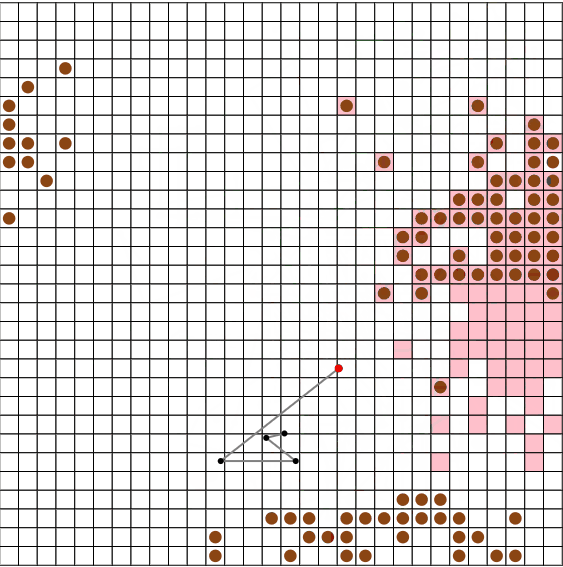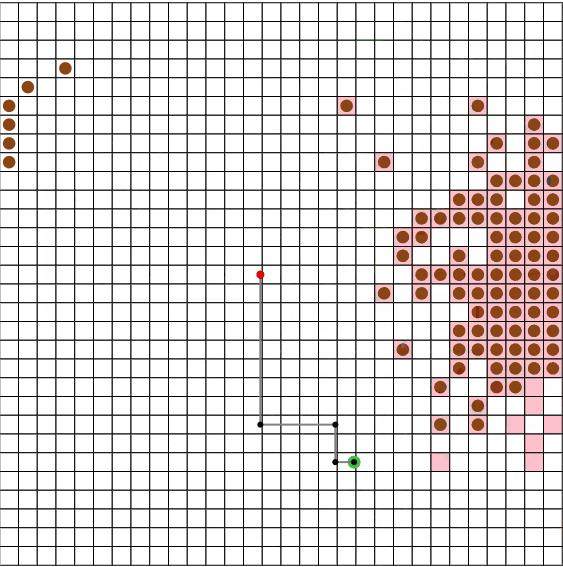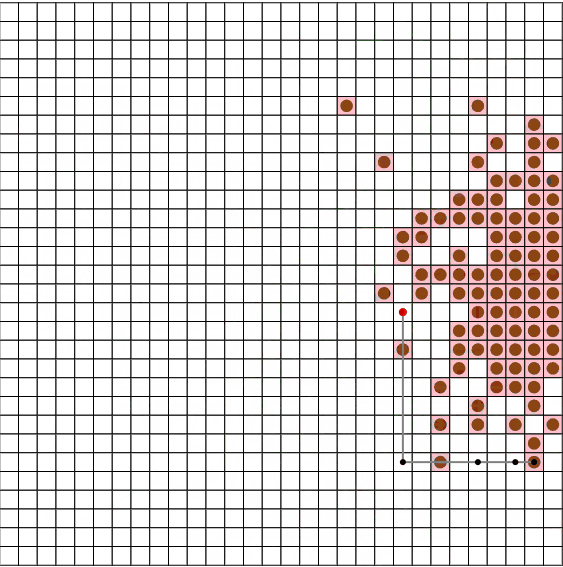
N=10, M = 50, V = 5のseed = 0で試してみたところ、今回の手法(上段)の場合は78ターン、前回の手法(下段)では156ターンでした。



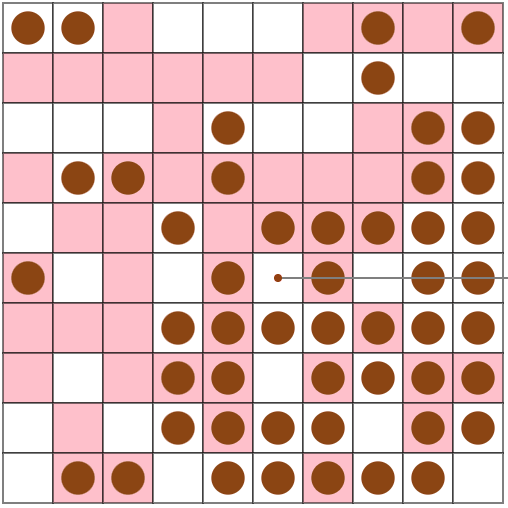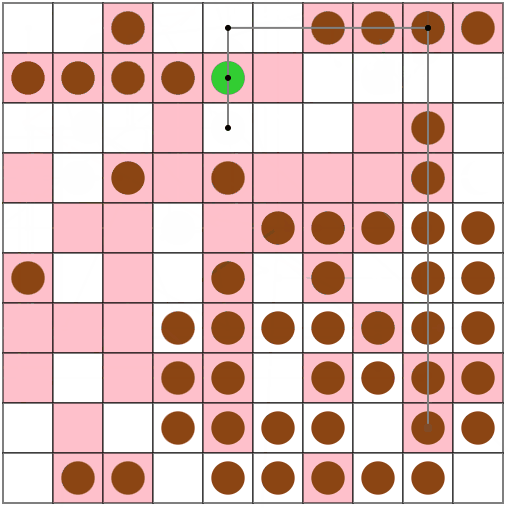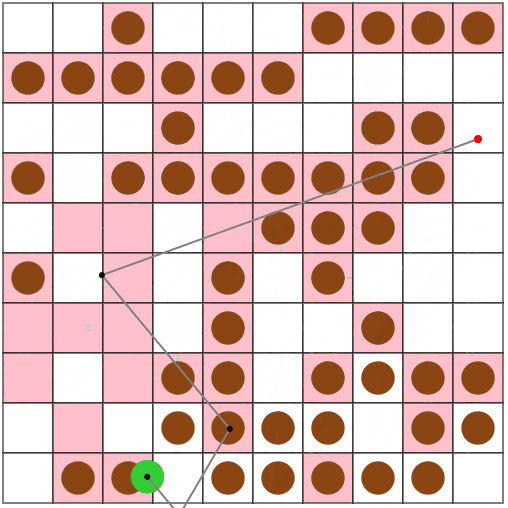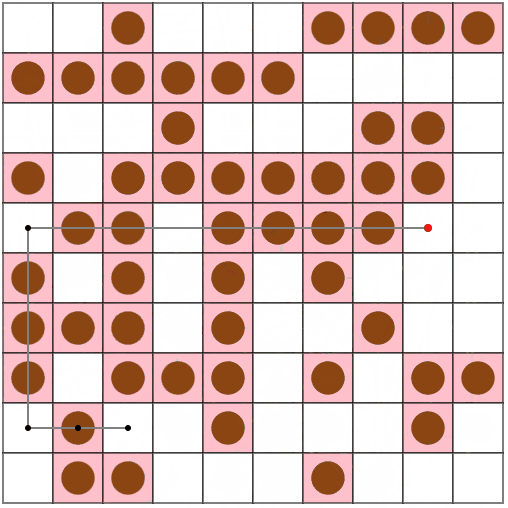
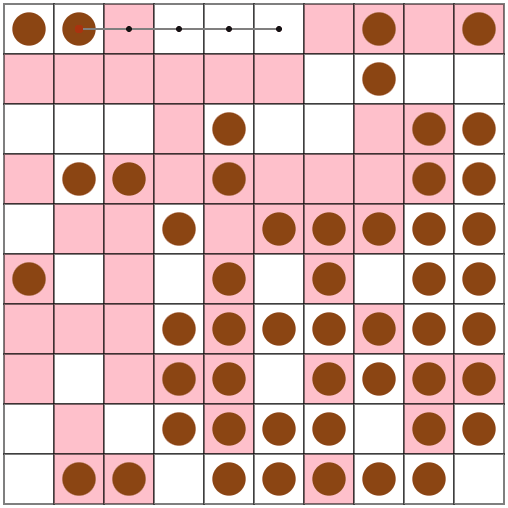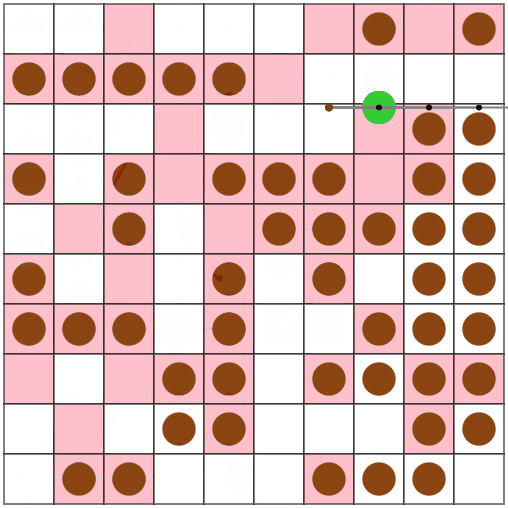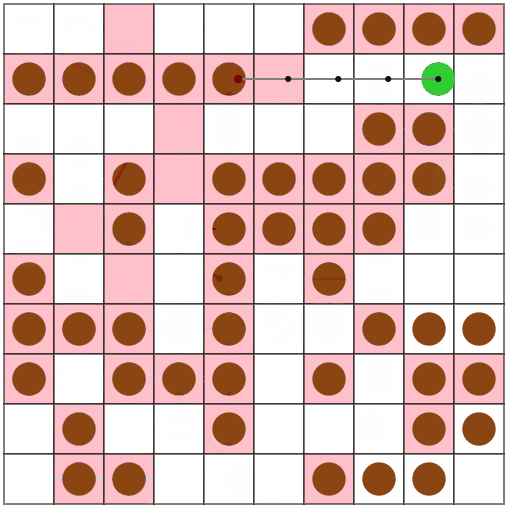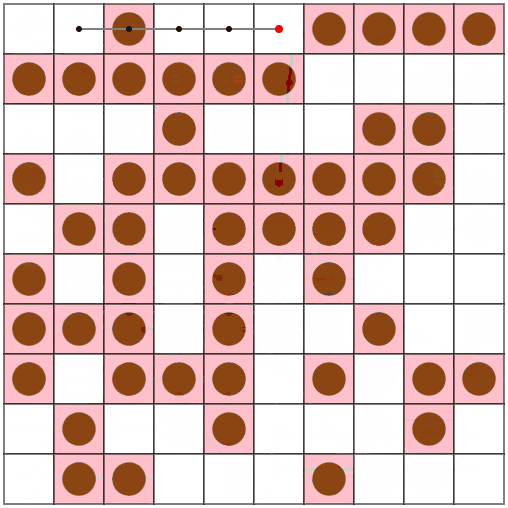
また、N = 30, M = 90, V = 5のseed = 13のような、「広い盤面でたこ焼きの数が少ない場合」に、特に前回の手法と大きな差が出ているようです。

今回の手法(上段)では496ターン、前回の手法(下段)では1247ターンでした。




 感想本番から2週間以上経っての延長戦でしたが、とても多くの気づきが得られました。
「16-8-4-2-1アームで盤面全体をカバーする」ことや、「事前に順運動学を全パターン試して、逆運動学のテーブルを作っておく」といったノウハウを新しく学べたのはとても大きいです。
また、アームの長さが足りない場合にも対応できるように平行移動も実装したため、プログラムとしてはそこそこ大きくなりましたが、メイン部分のプログラムはほぼ一発完動させることができました。自分でも驚きでした。天才かもしれん。
これからのAHCでも、延長戦は欠かさずやっていきたいと思います。