【週末研究】03. 単語とグラフ構造の関係 - トピックモデルのグラフ表現

グラフの行列表現の自然言語処理における意味

今回は、グラフの行列表現の数学的意味、自然言語における意味についてトピックモデル(LSI, LDA)を例に挙げて考察していきます。

---

線形写像と基底変換との関係

まずは、線形写像と基底変換について見ておきます。

２つのベクトル空間($U, V$)について、$\alpha, \alpha'$ を $U$ の ２つの座標系、 $\beta, \beta'$ を $V$ の ２つの座標系、とします。

この時、線形写像 $t: U \rightarrow V$ の表現行列 $T$ が、基底変換(i.e. 座標系の変換：$\alpha \rightarrow \alpha', \beta \rightarrow \beta'$)により、どう変わるかを見ておきます。

尚、このセクションの内容は、Wikipediaの基底変換 をベースに作成しています。

外観図

基底変換と線形写像との間の関係の外観を以下に示します。

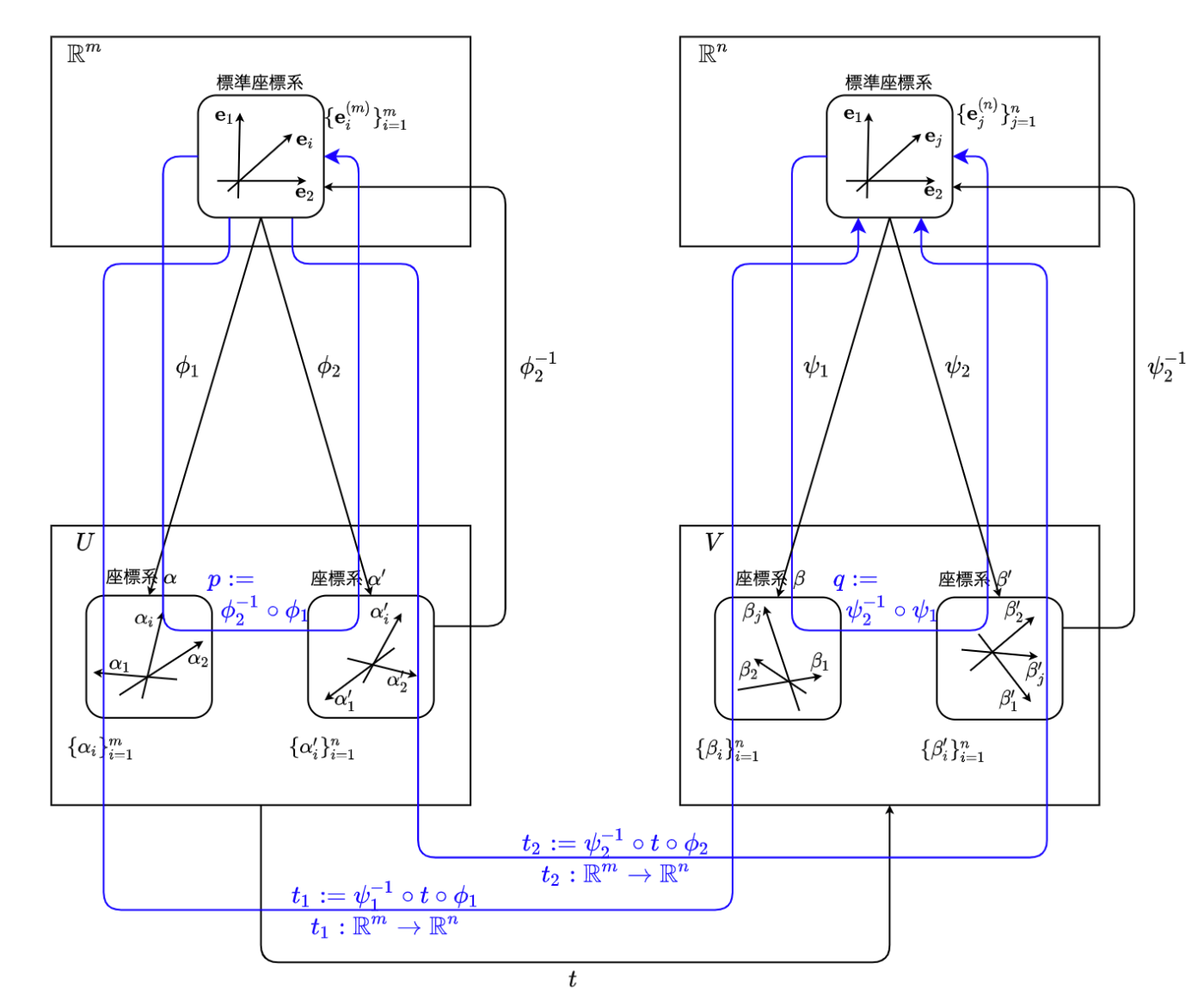
この時、線形写像 $t_1, t_2$ の間に、以下のような関係がなり立ちます。

$$t_2 = q \circ t_1 \circ p^{-1}$$

表現行列で表すと、

$$T_2 = Q T_1 P^{-1}$$

と表せます。

記号の定義

正確な理解のために、記号の定義を、以下のようにしておきます。

$\mathbb{R}^m, \mathbb{R}^n$ 上の標準座標系

$\mathbb{R}^m, \mathbb{R}^n$ 上の標準座標系 $\{ \mathbf{e}_i^{(m)} \}, \{ \mathbf{e}_i^{(n)} \}$ を以下のように定義しておきます。これは、一般的な定義かと思います。

$$\begin{align} \mathbf{e}_i^{(m)} &:= \overset{i}{(0, ..., 0, 1, 0, ..., 0)} \in \mathbb{R}^m \\ \mathbf{e}_j^{(n)} &:= \overset{j}{(0, ..., 0, 1, 0, ..., 0)} \in \mathbb{R}^n \\ \end{align}$$

ベクトル空間

2 つのベクトル空間について、いくつか定義をしておきます。

$U$ : $m$ 次元ベクトル空間
$V$ : $n$ 次元ベクトル空間

ベクトル空間$U, V$上の座標系

以下のように、ベクトル空間$U$ 上の２つの座標系を、$\alpha, \alpha'$ とし、
ベクトル空間$V$ 上の２つの座標系を、$\beta, \beta'$ としておきます。

$$\begin{align} \alpha &:= \{\alpha_1, ..., \alpha _m\}, & \alpha _i \in U, & ~~ i=1, ..., m \\ \alpha' &:= \{\alpha'_1, ..., \alpha' _m\}, & \alpha'_i \in U, & ~~ i=1, ..., m \\ \beta &:= \{\beta_1, ..., \beta _n\}, & \beta _j \in V, & ~~ j=1, ..., n \\ \beta' &:= \{\beta'_1, ..., \beta' _n\}, & \beta'_j \in V, & ~~ j=1, ..., n \\ \end{align}$$

座標同型

座標同型についても定義しておきましょう。

$\phi : \mathbb{R}^m \rightarrow U$ が、ベクトル空間 $U$ の座標系 $\alpha$ に対する座標同型であるとは、$\phi(e_i^{(m)}) = \alpha_i$ を満たす唯一の線型写像とします。

ベクトル空間$U, V$上の座標同型

以下のように、ベクトル空間$U$ 上の2つの座標同型を $\phi_1, \phi_2$ とし、
ベクトル空間$V$ 上の2つの座標同型を $\psi_1, \psi_2$ としておきます。

$\phi_1 : U, \alpha$ に対する座標同型; $\phi_1(e_i^{(m)}) = \alpha_i$
$\phi_2 : U, \alpha'$ に対する座標同型; $\phi_2(e_i^{(m)}) = \alpha'_i$
$\psi_1 : U, \beta$ に対する座標同型; $\psi_1(e_i^{(n)}) = \beta_i$
$\psi_2 : U, \beta'$ に対する座標同型; $\psi_2(e_i^{(n)}) = \beta'_i$

ベクトル空間上の線形写像

ベクトル空間$U$ から $V$ への線形写像を $t : U \rightarrow V$ とし、$t$ の表現行列を、$T \in M(n, m)$ とします。

ここで、$M(n, m)$ は、実数 $\mathbb{R}$ 上の $(n, m)$ 行列全体の集合とします。

ベクトル空間$U, V$ を経由する、$\mathbb{R}^{m}$ から $\mathbb{R}^{n}$ への線型写像

線形写像 $t_1, t_2 : \mathbb{R}^m \rightarrow \mathbb{R}^n$ を以下のように定義します。

$t_1 := \psi_1^{-1} \circ t \circ \phi_1$
$t_2 := \psi_2^{-1} \circ t \circ \phi_2$

また、$t_1, t_2$ の表現行列を、$T_1, T_2$ としておきます。

実ベクトル空間上の座標変換

$m$ 次元実ベクトル空間上の線形写像、$p$ と $n$ 次元実ベクトル空間上の線形写像、$q$ を以下のように定義しておきます。

$p := \phi_2^{-1} \circ \phi_1; ~~ p : \mathbb{R}^m \rightarrow \mathbb{R}^m$
$q := \psi_2^{-1} \circ \psi_1; ~~ q : \mathbb{R}^n \rightarrow \mathbb{R}^n$

すると、$p, q$ は、同じ実ベクトル空間上の座標変換になることに注意しておきます。

また、$p, q$ の 表現行列を $P, Q$ としておきます。

$t_1, t_2$ の関係

ここで、 線形写像 $t_1, t_2 : \mathbb{R}^m \rightarrow \mathbb{R}^n$ の関係を見ていきます。

$$\begin{align} t_2 & = \psi_2^{-1} \circ t \circ \phi_2 \\ &= \psi_2^{-1} \circ (\psi_1 \circ \psi_1^{-1}) \circ t \circ (\phi_1 \circ \phi_1^{-1}) \circ \phi_2 \\ &= \psi_2^{-1} \circ \psi_1 \circ (\psi_1^{-1} \circ t \circ \phi_1) \circ \phi_1^{-1} \circ \phi_2 \\ &= \psi_2^{-1} \circ \psi_1 \circ t_1 \circ \phi_1^{-1} \circ \phi_2 \\ &= (\psi_2^{-1} \circ \psi_1) \circ t_1 \circ (\phi_1^{-1} \circ \phi_2) \\ &= (\psi_2^{-1} \circ \psi_1) \circ t_1 \circ (\phi_2^{-1} \circ \phi_1)^{-1} \\ &= q \circ t_1 \circ p^{-1} \\ \end{align}$$

つまり、$p^{-1}$ によって座標変換($p$ の逆座標変換)を行い、$t_1$ を施した後、$q$ で座標変換を行うことで、$t_2$ と同等の線形写像を得る、ということです。

特に、表現行列で表すと、

$$T_2 = Q T_1 P^{-1}$$

として、$T_2$ を、座標変換行列$P, Q$ と、ある座標系での線形写像の表現行列 $T_1$ を用いて行列分解できることを意味しています。

---

特異値分解 for LSI

次に、特異値分解と座標変換との関係を見ていきます。

特異値分解は、トピックモデルの１つである、LSI (Latent Semantic Index) で利用されています。 より具体的には、LSI は、 TF-IDF 行列の特異値分解です。

特異値分解の定義

$m \times n$ 行列 $A$ を、以下の右辺のように３つの行列の積に分解することを特異値分解と呼びます。ただし、この記事では、$m$ を単語などのトークンの語彙数、$n$ を文書数としていきます。

$$A = U \Sigma V^{\mathsf{T}}$$

ここで、

• $U$ : $m$次直交行列 ... i.e. $U^{-1} = U^{\mathsf{T}}$
  • 複素行列上では、ユニタリだがここでは実空間に限っている
• $V$ : $n$次直交行列 ... i.e. $V^{-1} = V^{\mathsf{T}}$
  • 複素行列上では、ユニタリだがここでは実空間に限っている
• $\Sigma$ : $m \times n$ 行列で、対角成分のみの行列

i.e.

$$\begin{align} UU^{\mathsf{T}} &= U^{\mathsf{T}}U = I_m; & [I_m]_{ij} = \delta_{ij} \\ VV^{\mathsf{T}} &= V^{\mathsf{T}}V = I_n; & [I_n]_{ij} = \delta_{ij} \\ \delta_{ij} &:= \begin{cases} 1 & (i = j) \\ 0 & (i \neq j) \\ \end{cases} \\ [\Sigma]_{ij} &= \begin{cases} \sigma_{i} & (i = j) \\ 0 & (i \neq j) \\ \end{cases} \end{align}$$

図で表現すると以下のようになります。

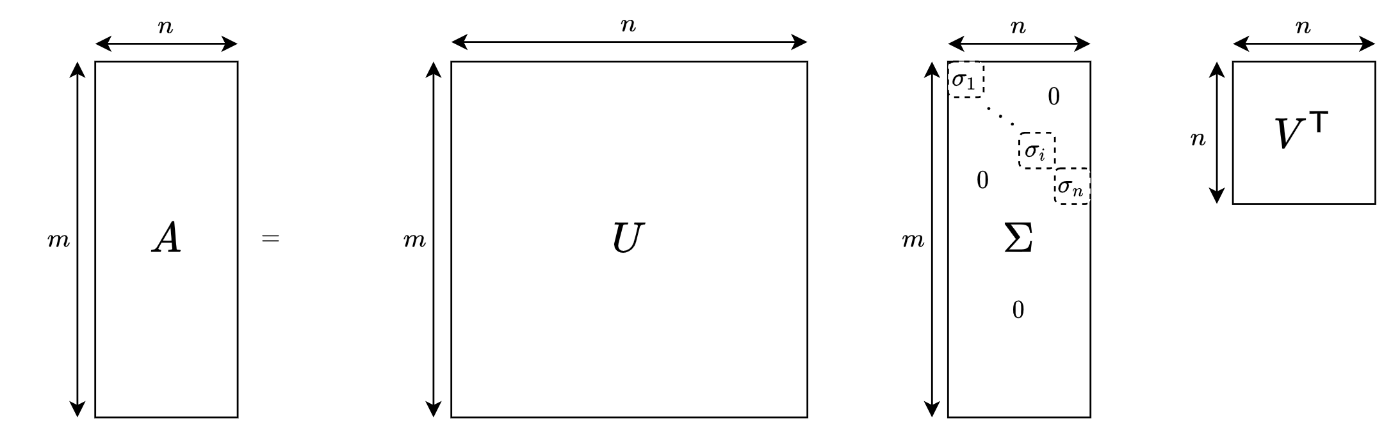
ここで、この図が表している式 $A = U \Sigma V^{\mathsf{T}}$と、線形写像の座標変換の式 $T_2 = Q T_1 P^{-1}$ を比べると(特に、$V^{\mathsf{T}} = V^{-1}$ であることを踏まえると)、特異値分解は、座標変換を伴って線形写像の表現行列の変換として見ることができるということです。つまり、$T_2 = A, Q = U, T_1 = \Sigma, P^{-1} = V^{-1} = V^{\mathsf{T}}$ としてみるということです。

---

さて、次元単位で各線形写像の表現行列の次元・軸（変数）の対応を図示すると以下のようになります。

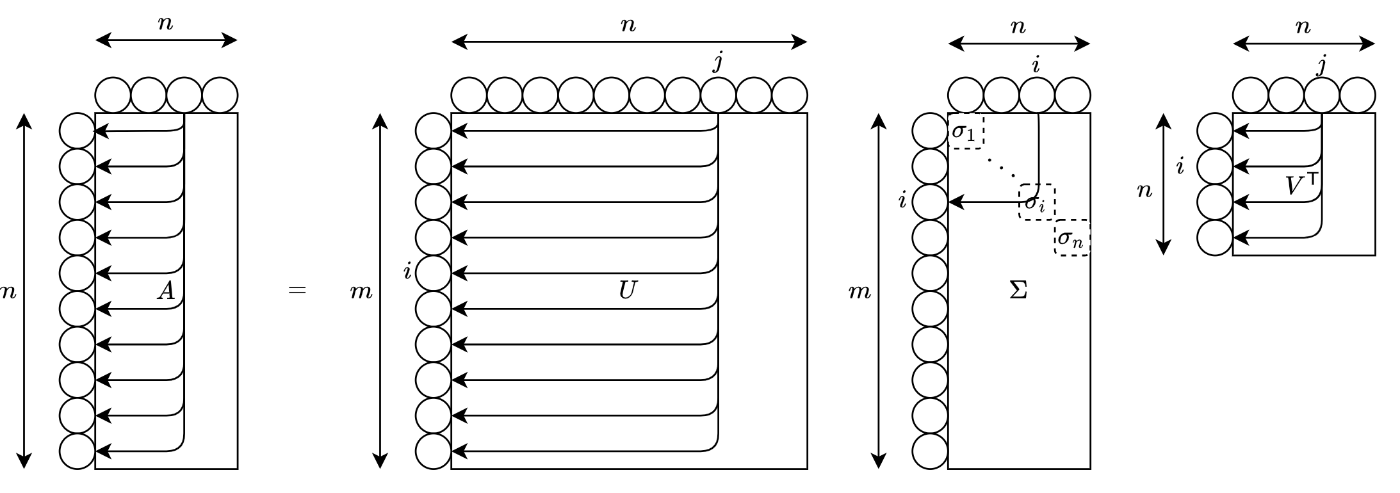
つまり、$V^{\mathsf{T}}$ では、各文書を変数・次元・軸としていた座標系($V^{\mathsf{T}}$の行ベクトルの列成分($\leftrightarrow$))から、それらの成分を合成した、座標系($V^{\mathsf{T}}$の列ベクトルの行成分($\updownarrow$))に変換し、その座標系を $\Sigma$ で (各$\sigma_i$ でスケール)した座標系に変換しています。最後に、単語の座標系($U$の行ベクトルの列成分$(\leftrightarrow$))を、単語の別の座標系($U$の列ベクトルの行成分$(\updownarrow$))に変換しています。

この解釈は、前回 見た通り、行列をグラフと見た時にグラフ上の関係(エッジ)が遷移・合成する重みに対応していることからわかります。また、行列の積の意味を考えても自然にわかるでしょう。

---

別の視点として、上の図を参考に、以下のようなニューラルネットワークFFN(i.e. グラフ構造) としても表現できることにも触れておきます。 ただし、一般的なニューラルネットワークモデルの書き方とは異なり、右から入力される図になっている点にご注意ください。

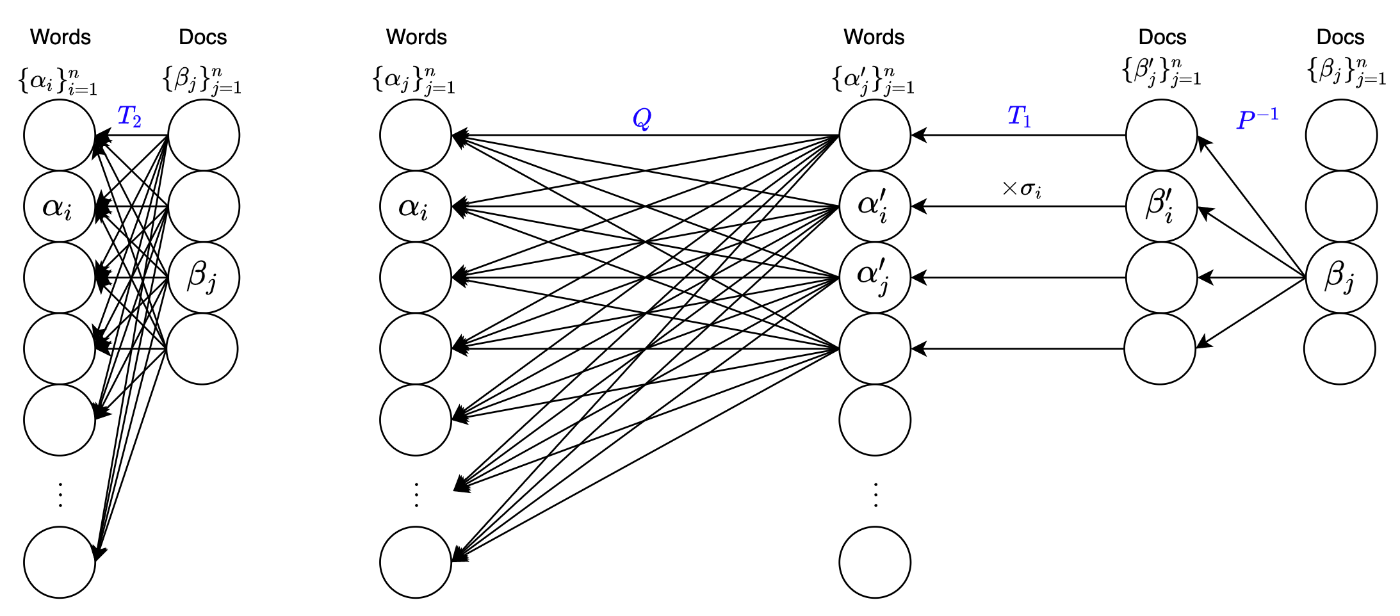
このモデル図からだと先ほどの図よりも、容易に座標変換との対応づけがしやすくなるかもしれません。
各Docs の標準座標系からDocs の別の座標系に変換され、スケールすることで Words の座標系へ変換されます。最後に、スケールによって得られた Words の座標系から Words の標準座標系に変換されるとわかります。

特に、$\beta'$ から $\alpha'$ への座標変換では、スケールされるだけであるため、$\beta'$ と $\alpha'$ は本質的に同じ座標系を指していることがわかります。つまり対応する各座標の基底ベクトルの長さが異なるだけということで、意味としては同じ座標系を指していると考えられます。

さらに言うと、この文書集合の合成、単語集合の合成から得られる軸の座標系($\beta', \alpha'$)に、トピックと名づけた、と考えると良いでしょう。

つまり、特異値$\{\sigma_i\}_i$ を大きい順に並べた時に、上位($k$ 個など)の特異値に対応する軸をピックアップすることは、トピックをピックアップすることに対応することも、理解しやすくなるかと思います。言い換えると、ピックアップしたトピックに含まれる単語は、$U$ から特定でき、ピックアップしたトピックを含む文章(トピックを重みづける学習文書)は、$V$ から特定できるということも、納得しやすいかと思います。

まとめると、単語と文書の関係を表したグラフの隣接行列である BoW や TF-IDF などを、特異値分解することは、座標変換の合成、つまり、単語-トピック(単語座標の別座標系)間の関係を表現するグラフの隣接行列や、文書-トピック(文書座標の別座標系)間の関係を表すグラフの隣接行列に、分解できることを意味しています。すなわち、単語-文書間の関係グラフ$A$を、単語-トピック間の関係グラフ$V$と、文書-トピック間の関係グラフ$U$の合成・連結関係(行列積)に分解することを意味しています。

---

LDA (Latent Dirichlet Allocation)

次は、トピックモデルとしてよく使われるであろう、LSIの確率モデルPLSIのベイズ化である LDA について、行列表現(グラフ構造としての表現、隣接行列)との関係を見ていきます。

LDA のグラフィカルモデル

まずは、ベースとなるLDAのグラフィカルモデルを見てみましょう。

$\alpha, \beta$ を所与のパラメータ（もしくは、学習パラメータ）として、$\varphi, \theta$ を生成し、その後、$Z, W$ と生成するモデルになります。

$W, Z, \theta, \varphi$ の同時分布は、上記図の右側の式の通りに分解されます。確率変数ベクトルの $W, Z, \theta, \varphi$ の各確率変数(e.g. $\theta_j^{(d)}$ など) が、互いに独立、もしくは、条件付き独立であることを仮定している(もしくは、平均場近似的に近似している)と思われます。

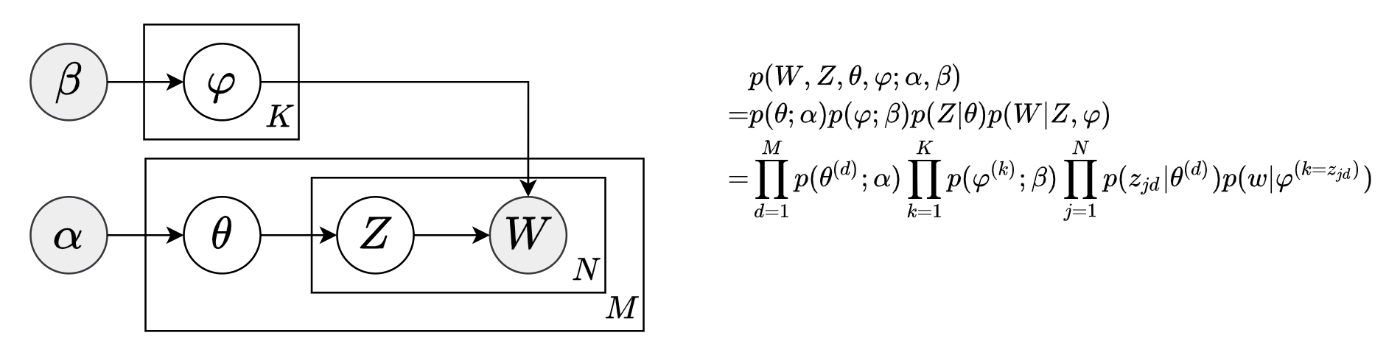
LDA のモデル図 (RAW文書データ)

さて、上記グラフィカルモデルをもう少し具体的に、より正確に図で理解したいと思います。しかし、なかなか自分が納得できそうな図をWeb上で見つけられなかったため、Wikipedia - Latent Dirichlet allocation を参考に下のような図に起こしました。(つまり、図中の各記号は、このWikipedia の内容に従っています。)

$Z$ や $W$ が、語彙数である $V$ を使った$V \times M$ 行列ではなく、$N \times M$ 行列である点に注意します。ここで、$N$: 単語の出現数(同じ単語は何回か出現しうる)、$M$: 文書数 を意味しています。特に、$W$ を単語毎に集計すると、各単語の出現数になり BoW になる点に注意します。

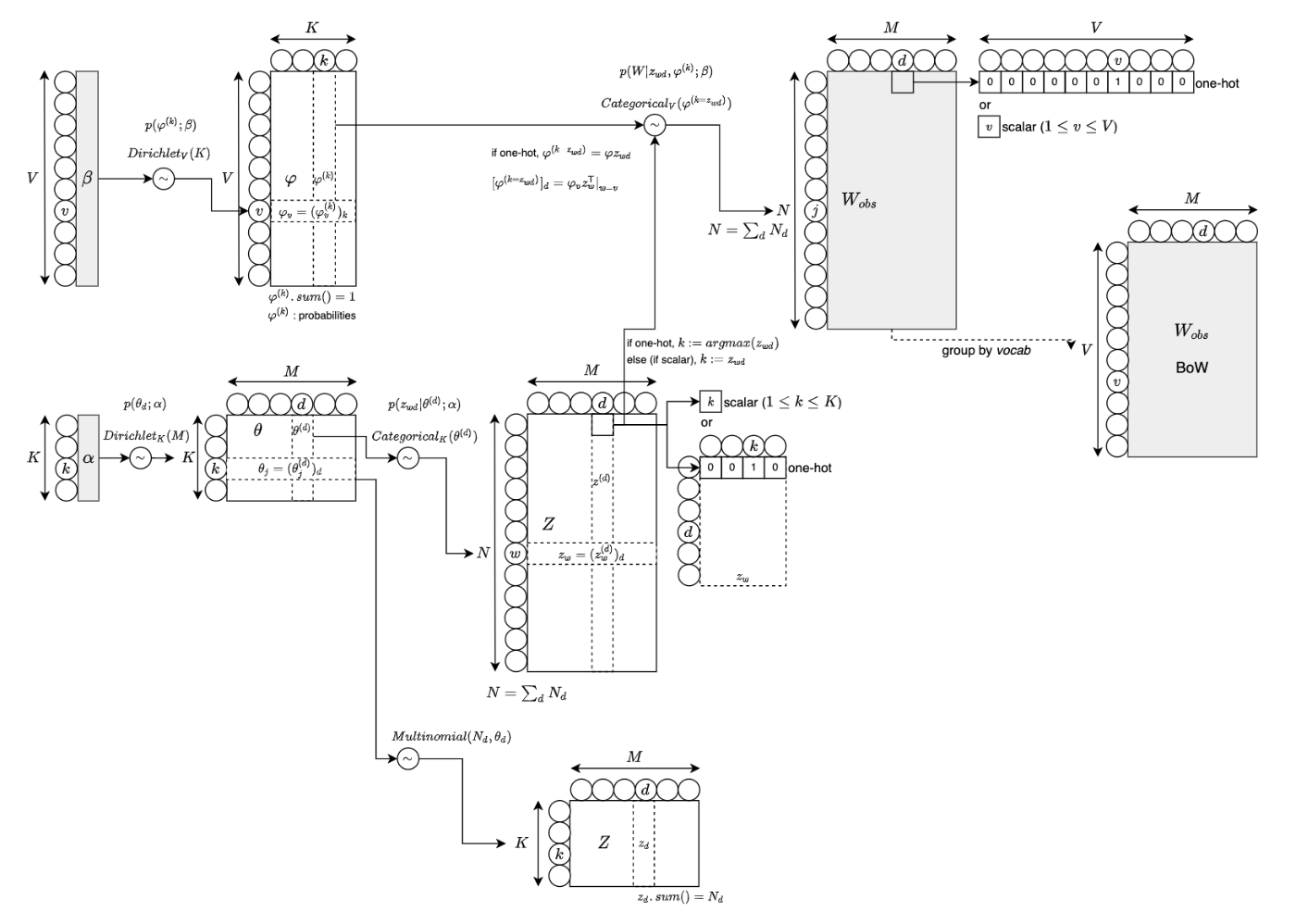
さて、LSI と比較して考えてみます。LSIでは、単語とトピック、文書とトピックの関係を表現した $\varphi, \theta$ に行列分解していました。LDA では、ベイズモデル化し、EMアルゴリズムや変分推定などにより、$\varphi, \theta$ を算出しているという点が類似点であり明確な相違点になります。
つまり、BoW などの観測データを行列の積という構造に分解・構造化したものが LSI であり、観測データをベイズモデル（グラフィカルモデル）で分解・構造化したもの(特に、事前分布をディリクレ分布とする)が、LDA と言えるでしょう。

LDA のモデル図 (BoW文書データ)

以下の図は、BoW を観測データとした場合の図になります。

$\varphi Z$ で表現されている行列が、BoW を生成するための重みパラメータになります。特に、$\varphi Z^{(d)} \in \mathbb{R}^{V}$ を、$\varphi Z^{(d)}.sum() = 1$ になるように、確率的に規格化すれば、学習対象の各文書における各語彙の発生確率として扱えます。

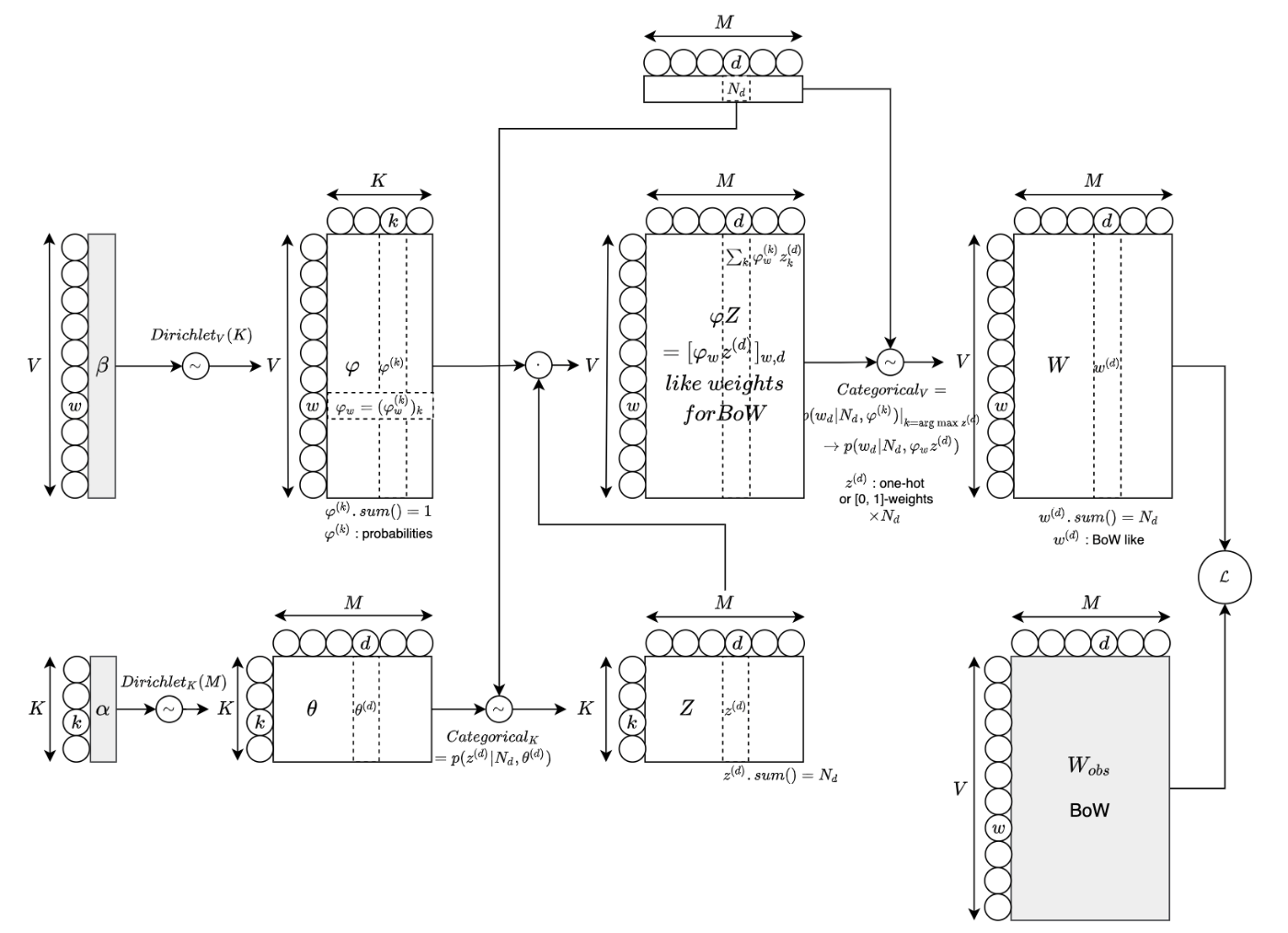
この図は、ニューラルネットワークでのモデル化としてもみることができます。つまり、図の右上の$W$ を生成し、学習データの$W_{obs}$ になるように学習するモデルとして見ることができます。もちろん、$W$ を生成せず、$\varphi Z$ のラベルデータとなるように、$W_{obs}$ から各文書における各語彙の発生確率を算出して、$\varphi Z$ を確率的に規格化した行列を再生できるように学習させる方法もあるでしょう。自己教師学習的に(中間的な特徴量も学習させるように)、$\varphi Z, W$ の双方を再生できるように学習する、というやり方ももちろん有意義でしょう。loss 関数は、差分を小さくするような関数や、尤度を最大化するようなものなど、一般的に用いられる loss 関数を用いることから評価を始めるとよさそうです。

さて、各行列（テンソル）を、グラフ構造の隣接行列として見ると、$\varphi$ は、単語とトピックの関係を表すグラフ、$\theta$ は、文書とトピックの関係を表すグラフとして捉えることができ、サンプリング処理により、別のグラフ(隣接行列)を生成したり、行列積によりグラフを合成したりして、$W_{obs}$ という単語と文書間の関係グラフを生成するモデルとして見ることができます。つまり、グラフを別のグラフに変換し、合成するモデルが LDA という見方もできるでしょう。

gensim, sklearn の LDA

LDA モデルは、sklearn, gensim から使うことができます。コードを見た感じ、いずれもEMアルゴリズムで学習しているようです。

sklearn の LDAモデル (LatentDirichletAllocation) は、$\alpha, \beta$ を固定して(引数で指定して), $\varphi$ を求め、lda.components_ として更新され参照可能になっています。

gensim の LDAモデル (LdaModel) は、$\alpha, \beta$ (※ gensim の実装では、$\beta$ が 変数 eta) も学習可能な実装になっていて、$\varphi$ は、lda.expElogbeta 変数として更新され参照可能になっています。

また、gensim の LDAモデルの実装では、$N \times M$ のデータ($W$)を入力としています。 sklearn の LDAモデルの実装では、$V \times M$ のデータ($W$; i.e. BoW)を入力としています。

以下にサンプルコードを載せておきます。

データをダウンロード

from sklearn.datasets import fetch_20newsgroups

d = fetch_20newsgroups()

N = 1000
X = d.data[:N]
y = d.target[:N]

sklearn のサンプルコード

import numpky
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import LatentDirichletAllocation

bow = CountVectorizer(min_df=0.04, stop_words="english")
X_bow = bow.fit_transform(X, y)
feature_names = numpy.array(bow.get_feature_names_out())

K = 50
beta = 1/len(feature_names)
# beta = 1/K        # vocab が多すぎる場合は、0 につぶれないように、1/K (デフォルト値)で代替する
print("beta:", beta)
lda = LatentDirichletAllocation(n_components=K, max_iter=100, n_jobs=-1, topic_word_prior=beta)
lda.fit(X_bow)

print(lda.components_.shape)       # (K, V)

gensim のサンプルコード

from gensim.corpora.dictionary import Dictionary
from gensim.parsing.preprocessing import remove_stopwords
from gensim.models import LdaModel

# cf. from sklearn code
import re
token_pattern=r"(?u)\b\w\w+\b"
tokenizer = re.compile(token_pattern).findall

from sklearn.feature_extraction._stop_words import ENGLISH_STOP_WORDS

def filter_sw(tokens: list):
    return [tkn for tkn in tokens if tkn.lower() not in ENGLISH_STOP_WORDS]

def do_tokenize(text: str):
    tokens = tokenizer(remove_stopwords(text))
    return filter_sw(tokens)

tokenized = [do_tokenize(doc) for doc in X]
dct = Dictionary(tokenized)
X_nummed = [dct.doc2bow(docwords) for docwords in tokenized]

lda = LdaModel(X_nummed, num_topics=K, iterations=100, alpha=1/K, eta=1/K)
# lda = LdaModel(X_nummed, num_topics=K, iterations=100, alpha="auto", eta="auto")      # ディリクレ分布のパラメータを学習させたい場合は、こちら

print(lda.expElogbeta.shape)       # (K, N)

サンプルコードの全体(Colab)は、こちら です。Colab のコードでは、トピック毎の発生確率が高い単語とその発生確率を表示しています。ご参考までに。

まとめ

• LSI(特異値分解)は、座標変換の合成として見ることができます
  • 特にトピックの座標系へ変換する行列$U, V$と縮尺する行列$\Sigma$ に分解・算出します
  • LDA でいうと、$\varphi=U, \theta=V$ に分解・構造化するモデルと言えるでしょう
  • グラフ上の意味としては、単語-文書間の関係グラフ$A$を、単語-トピック間の関係グラフ$V$と、文書-トピック間の関係グラフ$U$の合成関係(行列積/グラフの連結関係)に分解することを意味しています
• LDA は、グラフィカルモデル(ベイズモデル)をベースに構造化し、$\alpha, \beta, Z, W$ の事後分布を学習し、$\varphi, \theta$ を推定・算出します
  • LDA もニューラルネットワーク風にグラフで表現することで、DLフレームワークを使っても学習、推定ができそうです
  • この時、中間出力を使って自己教師学習的なモデルにもできそうです
  • gensim のLDAモデルは、生文書を数値化したデータを入力とし、sklearn のLDAモデルは、BoW を入力としています
  • グラフ上の意味としては、$\varphi$ は、単語とトピックの関係を表すグラフ、$\theta$ は、文書とトピックの関係を表すグラフとして捉えることができます
    • つまり、関係グラフを別の関係グラフに変換したり、合成(連結)したりするモデルが LDA (ベイズモデル) という見方もできます
• 以上から
  • BoW/TF-IDF などの観測データを行列(座標変換)の積という構造に分解・構造化したものが LSI(特異値分解)
    • 単純に２つのグラフの連結関係に分解・構造化
  • 観測データをベイズモデル（グラフィカルモデル）で分解・構造化した(特に、事前分布をディリクレ分布とする)ものが、LDA
    • 複数のグラフ間で変換、連結する関係に分解・構造化
  • と考えるとよいでしょう
• 行列をグラフとして見ることで、これまでの手法の拡張関係を外観でき、新しい視点でのモデル化ができそうな、そんな予感がしています

---

参考記事 / 参考URL

• 基底変換関係
  • Wikipedia - 基底変換
  • 線形代数：固有値分解、特異値分解、疑似逆行列
• トピックモデル関係
  • Wikipedia - Latent Dirichlet allocation
  • 特異値分解 (SVD) と多次元解析
  • 【入門】トピックモデルとは？トピック分析の３つの手法を解説
  • Theory and Applications of Correspondance Analysis; p177
  • Wikipedia - Dirichlet distribution
  • Wikipedia - Multinomial distribution
  • Wikipedia - Categorical distribution
  • Wikipedia - Statistical inference
  • Wikipedia - Dirichlet-multinomial distribution
  • Wikipedia - Compound probability distribution

---

次回は、トピックモデルなどのトピックに名前を付与するモデルを設計してみようと思います。乞うご期待！
ちなみに、前回はこちら