グラフの行列表現
今回は、グラフ構造を行列で表現する方法について見ていきます。
隣接行列
例で考えてみましょう。
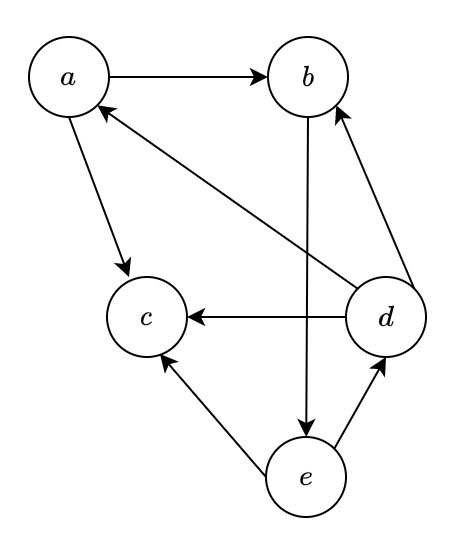
このグラフでの矢印を整理します。
- a \rightarrow b, c
- b \rightarrow e
- c \rightarrow なし
- d \rightarrow a, b, c
- e \rightarrow c, d
この関係(矢印の方向)を行列で表現すると以下のように表現できます。(この行列を A としておきます)
\begin{aligned}
A := \left [
\begin{array}{c:}
& a & b & c & d & e \\ \hdashline
a & 0 & 1 & 1 & 0 & 0 \\
b & 0 & 0 & 0 & 0 & 1 \\
c & 0 & 0 & 0 & 0 & 0 \\
d & 1 & 1 & 1 & 0 & 0 \\
e & 0 & 0 & 1 & 1 & 0 \\
\end{array}
\right]
\end{aligned}
a \rightarrow b, c は、行a の b, c 列を 1 として表現します。
\begin{aligned}
\left [
\begin{array}{c:}
& a & b & c & d & e \\ \hdashline
a & 0 & 1 & 1 & 0 & 0 \\
\end{array}
\right]
\end{aligned}
同様に、e \rightarrow c, d は、行e の c, d 列を1として表現します。
\begin{aligned}
\left [
\begin{array}{c:}
& a & b & c & d & e \\ \hdashline
e & 0 & 0 & 1 & 1 & 0 \\
\end{array}
\right]
\end{aligned}
残りも同じようにして、1 を埋めていくことで行列を構築していきます。
このようにして構築された行列 A を、隣接行列(adjacency matrix)と呼びます。
定式化
A = [a_{i,j}]_{i,j} について、ノード i, j 対する要素 a_{i,j} を以下のように定義します。
\begin{aligned}
a_{i,j} :=
\left \{
\begin{array}{l}
1 & if~i \rightarrow j \\
0 & otherwise \\
\end{array}
\right .
\end{aligned}
ここで、a_{i,j} == 0 は、ノード i, j の間に現時点では関係(エッジ)がない(関係があるとわかっていない状況も含む)ことを意味しています。
遷移と隣接行列
次に、グラフの有向矢印に沿った遷移と隣接行列の関係を見ていきます。
ノード集合 N_A := \{ a, b, c, d, e \} から 別のノード集合 N_X := \{ x, y, z \} への有向関係を持つグラフ G_1 を考えます。ここで、NLPの文脈では、各ノード集合の各ノードが単語やサブワードなどのトークンに対応すると考えていただければと思います。
G_1
同様にして、N_X から N_P := \{p, q\} への有向関係を持つグラフ G_2 を考えます。
G_2
この2つのグラフを行列で表現すると、以下のようになります。
\begin{aligned}
G_1 := \left [
\begin{array}{c:}
& x & y & z \\ \hdashline
a & 1 & 0 & 1 \\
b & 0 & 1 & 0 \\
c & 0 & 1 & 1 \\
d & 1 & 1 & 1 \\
e & 1 & 1 & 0 \\
\end{array}
\right]
\end{aligned}
\begin{aligned}
G_2 := \left [
\begin{array}{c:}
& p & q \\ \hdashline
x & 1 & 0 \\
y & 1 & 1 \\
z & 1 & 1 \\
\end{array}
\right]
\end{aligned}
一般的には、すべてのノードを行と列に登場させて、以下のようにn \times n 行列で表現するでしょう。
\begin{aligned}
G := \left [
\begin{array}{c:}
& a & b & c & d & e & x & y & z & p & q \\ \hdashline
a & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 \\
b & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
c & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 \\
d & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 0 \\
e & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0 \\
x & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\
y & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\
z & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\
p & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
q & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right]
\end{aligned}
今回は、どちらで表現しても同等であることを見ていきます。
実際に、python コードで実験・検証してみます。まずは、numpy で、行列を定義し、行列の積 G_1 \cdot G_2 を計算してみます。
import numpy
G1 = numpy.array([
[1, 0, 1],
[0, 1, 0],
[0, 1, 1],
[1, 1, 1],
[1, 1, 0],
])
G2 = numpy.array([
[1, 0],
[1, 1],
[1, 1],
])
G1.dot(G2)
出力結果は、以下の通りです。
array([[2, 1],
[1, 1],
[2, 2],
[3, 2],
[2, 1]])
つまり、
\begin{aligned}
G_1 \cdot G_2 = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 2 & 1 \\
b & 1 & 1 \\
c & 2 & 2 \\
d & 3 & 2 \\
e & 2 & 1 \\
\end{array}
\right]
\end{aligned}
ということです。
ここで、グラフを連結させた図を見てみます。
a 行に着目すると、a \rightarrow p の経路が a \rightarrow x \rightarrow p, a \rightarrow z \rightarrow p の2通りあり、a \rightarrow q の経路が a \rightarrow z \rightarrow q の 1通りであることがわかります。これは、以下のように G_1 \cdot G_2 の a 行の成分と一致します。
\begin{aligned}
[G_1 \cdot G_2]_{a} = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 2 & 1 \\
\end{array}
\right]
\end{aligned}
同じように、a 行に着目すると d \rightarrow p の経路は、 d \rightarrow x \rightarrow p, d \rightarrow y \rightarrow p, d \rightarrow z \rightarrow p の 3通り。d \rightarrow q の経路は、d \rightarrow y \rightarrow q, d \rightarrow z \rightarrow q の 2通りあり、G_1 \cdot G_2 の d 行の成分と一致します。
\begin{aligned}
[G_1 \cdot G_2]_{d} = \left [
\begin{array}{c:}
& p & q \\ \hdashline
d & 3 & 2 \\
\end{array}
\right]
\end{aligned}
以上のことから、グラフ G_1, G_2 を連結させたグラフに置いて、各ノード間の経路の数を表現しているのが 2つの隣接行列の積 G_1 \cdot G_2 であることがわかります。グラフの連結と対応する隣接グラフの積が対応するという非常に直感的にも自然な解釈ができる点が興味深いところです。
今回は、G_1 の列ノードとG_2の行ノードが一致するケースを扱いましたが、一般には一致するとは限りません。実用的には、与えられた G_1の列ノードとG_2の行ノードを合わせたノードの和集合を新たな G_1の列ノードとG_2の行ノードとすることで、全く同じ議論が展開できる点に注意します。(特に、もともとなかったノードに対する成分の値は、0 で埋めます)
では、グラフ G_1, G_2 の全てのノードを登場させたグラフ G で同じように見ていきます。こちらも python コードで確かめてみます。
G = numpy.array([
[0, 0, 0, 0, 0, 1, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
[0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
], dtype=numpy.int64)
G.dot(G)
出力結果は、以下の通りです。
array([[0, 0, 0, 0, 0, 0, 0, 0, 2, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 2, 2],
[0, 0, 0, 0, 0, 0, 0, 0, 3, 2],
[0, 0, 0, 0, 0, 0, 0, 0, 2, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]])
この出力結果は、以下の行列を意味しています。
\begin{aligned}
G \cdot G := \left [
\begin{array}{c:}
& a & b & c & d & e & x & y & z & p & q \\ \hdashline
a & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 \\
b & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\
c & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 2 \\
d & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 & 2 \\
e & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 \\
x & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
y & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
z & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
p & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
q & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right]
\end{aligned}
a, d 行に絞ってみると、先ほど、G_1 \cdot G_2 でみた結果と一致することがわかります。
\begin{aligned}
[G \cdot G]_{(a,d)} = \left [
\begin{array}{c:}
& a & b & c & d & e & x & y & z & p & q \\ \hdashline
a & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2 & 1 \\
d & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 3 & 2 \\
\end{array}
\right]
\end{aligned}
0 行列の部分を除くと以下と一致することに注意しておきます。
\begin{aligned}
[G \cdot G]_{(a,d), (p,q)} = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 2 & 1 \\
d & 3 & 2 \\
\end{array}
\right]
\end{aligned}
つまり、必要なノードだけを使った演算 G_1 \cdot G_2 と、全ノードを使った演算 G \cdot G は、同じ結果を導くということが言えます。(式で考えれば、ほぼ自明ですが、このように実際に計算することで、さらに実感が得られると思います)
これは、G のような大域的な巨大な行列を作らなくても、局所的な行列を使うことが可能であることを示唆している。
隣接行列の拡張
次に、各グラフのエッジの有無(重みが \{0, 1\})ではなく、任意の重みが付与されているケースを考えます。
例として、各重みが [0, 1] 区間の間の値を取るケースをグラフで表現してみます。
G_1 (mermaid による表示の大きさの関係で、縦長で表示しています)
グラフ G_1 を隣接行列風に表現してみます。
\begin{aligned}
G_1 := \left [
\begin{array}{c:}
& x & y & z \\ \hdashline
a & 0.93 & 0.32 & 0.18 \\
b & 0.20 & 0.57 & 0.60 \\
c & 0.96 & 0.65 & 0.75 \\
d & 0.65 & 0.75 & 0.96 \\
e & 0.01 & 0.11 & 0.30 \\
\end{array}
\right]
\end{aligned}
同様に、グラフ G_2 を隣接行列風に表現してみます。
\begin{aligned}
G_2 := \left [
\begin{array}{c:}
& p & q \\ \hdashline
x & 0.66 & 0.81 \\
y & 0.87 & 0.96 \\
z & 0.72 & 0.64 \\
\end{array}
\right]
\end{aligned}
では、python コードで、G_1 \cdot G_2 を計算してみましょう。
G1 = numpy.array([
[0.93, 0.32, 0.18],
[0.2 , 0.57, 0.6 ],
[0.96, 0.65, 0.75],
[0.65, 0.75, 0.96],
[0.01, 0.11, 0.3 ]
])
G2 = numpy.array(
[[0.66, 0.81],
[0.87, 0.96],
[0.72, 0.64]
])
G1.dot(G2)
出力結果は、以下の通りです。
array([[1.0218, 1.1757],
[1.0599, 1.0932],
[1.7391, 1.8816],
[1.7727, 1.8609],
[0.3183, 0.3057]])
この結果は、以下のような行列を意味します。
\begin{aligned}
G_1 \cdot G_2 = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 1.0218 & 1.1757 \\
b & 1.0599 & 1.0932 \\
c & 1.7391 & 1.8816 \\
d & 1.7727 & 1.8609 \\
e & 0.3183 & 0.3057 \\
\end{array}
\right]
\end{aligned}
ノードa (a行)に絞ってみていきましょう。
グラフでの表現は、以下のようになります。
行列で表現してみます。
\begin{aligned}
[G_1]_{a} \cdot G_2 &=
\left [
\begin{array}{c:}
& x & y & z \\ \hdashline
a & 0.93 & 0.32 & 0.18 \\
\end{array}
\right]
\cdot
\left [
\begin{array}{c:}
& p & q \\ \hdashline
x & 0.66 & 0.81 \\
y & 0.87 & 0.96 \\
z & 0.72 & 0.64 \\
\end{array}
\right]
\\
& = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 0.93*0.66+0.32*0.87+0.18*0.72 & 0.93*0.81+0.32*0.96+0.18*0.64 \\
\end{array}
\right]
\end{aligned}
この計算式と上記グラフ(図)を見てみると、a \rightarrow p の経路である
a \xrightarrow{0.93} x \xrightarrow{0.66} p の経路上の全ての枝の重みの積(0.93*0.66)、
a \xrightarrow{0.32} y \xrightarrow{0.87} p の経路上の全ての枝の重みの積(0.32*0.87)、
a \xrightarrow{0.18} z \xrightarrow{0.72} p の経路上の全ての枝の重みの積(0.18*0.72)を加算した値であるとわかります。
つまり、
\begin{aligned}
[G_1]_{a} \cdot G_2 = \left [
\begin{array}{c:}
& p & q \\ \hdashline
a & 1.0218 & 1.1757 \\
\end{array}
\right]
\end{aligned}
は、a \xrightarrow{1.0218} p であり、a から p への重み(の総計)として考えてもよさそうです。これは、直感的な解釈に反しない解釈が得られていることにも注意します。(行列積により意味が変わらないということです)
特に、これは、ニューラルネットワークにおける、重みの計算と同じであることにも注意しておきます。
ノードと単語の関係
ここで、ノードを単語や単語集合(のラベル: 文、文書)として解釈してみましょう。
a \xrightarrow{1.0218} p の 1.0218 は、単語 a から 単語または単語集合 p への重みとして解釈できます。特に、a が 文書 p においてどれぐらい重要かを表す重みとして考えると、このグラフに対する行列表現は、TF-IDF (Term Frequency - Inverse Document Frequency) になることに注意します。
同様に、先ほど見た隣接行列風に、\{0, 1\} (拡張するなら、0以上の整数) で表現した行列に対しては、a が 文書 p に出現する回数(単語a から 単語集合p への(生成・出現)経路数=文グラフの数)とみなすと、BoW (Bag of Words) になることに注意します。
つまり、TF-IDF や BoW は、単語のグラフ表現の特殊系として考えることができるということを意味し、言い換えると、TF-IDF や BoW の拡張として、単語のグラフ表現が位置付けられる、と言えます。
このことから、単語のグラフ表現を考える意味が見出せるのではないでしょうか。
次回は、隣接行列によるグラフ表現の自然言語処理の文脈での意味について考察します
ちなみに、前回はこちら

Discussion