Parameter-Varying な系に対するKoopman作用素を用いたモデル化と制御：制御編

当記事は東京科学大学の藤井成美（https://www.linkedin.com/in/narumi-fujii-32304330b/ ）によって執筆されました

はじめに

本記事は，IEEE CDC 2023で発表されたParameter-Varying Koopman Operator for Nonlinear System Modeling and Controlという論文紹介の後編となります．前回のモデル化編ではParameter-Varyingな系に対するKoopman作用素を用いたモデル化を紹介したので，今回はそのモデルを用いた制御編となります．Koopman作用素理論によると，元の系が非線形系であったとしても，高次元空間へ観測関数によって射影した状態の時間発展考えることで線形系として記述することができます．モデル化編では，時間依存パラメータ$p={p}_k$を含むNonlinear Parameter-Varying system (NPVs)

$$\begin{align} {\bm x}_{k+1} = {\bm f} ({\bm x}_k,~{\bm u}_k,~{p}_k) \tag{1} \end{align}$$

に対して，eDMDと呼ばれるData-Driven型の手法により以下のようなLinear Parameter-Varying system (LPVs)を同定する方法を紹介しました．

$$\begin{align} {\bm y}_{k+1}&={\bm A}\left(p_k\right) {\bm y}_k+{\bm B}\left(p_k\right) {\bm u}_k \tag{2a}\\ {\bm x}_{k} &= {\bm C} {\bm y}_{k} \tag{2b} \end{align}$$

ここで，${\bm y}_k={\bm \Psi}_x({\bm x}_k)$であり一般に${\bm x}_k$よりも次元が高く，${\bm \Psi}_x$は観測関数です．式$\text{(2)}$はKoopman 作用素をParameter-Varyingな形で同定しているため，論文内では Parameter-Varying Koopman 作用素（PVKO）と呼ばれています．$p={p}_k$の時間変化を既知とすると，元の系の初期状態 ${\bm x}_0$が分かれば${\bm y}_0={\bm \Psi}_x({\bm x}_0)$と式$\text{(2a)}$から ${\bm y}_k$の時間発展を予測することができ，式$\text{(2b)}$によっていつでも元の系の状態空間に戻すことができます．つまり，式$\text{(1)}$のようなNPVsに対する制御設計を，式$\text{(2)}$のようなLPVsに対する制御設計に置き換えることができます．
MPCとは，Model Predictive Controlの略で近年の計算機の発達とともに確立された制御手法です．系の状態予測モデルに基づき，有限評価区間内の最適制御問題を実時間で数値的に解くという方法で，評価区間を後退させながら逐次的に制御入力を決定します．最適制御問題を実時間で解くために重要なことは，状態予測モデルが簡単であることです．特に，LPVなモデルを用いる場合はLPV MPCと呼ばれており，非線形な状態予測モデルを用いるよりも計算コストが低くなります．ここではPVKOとして同定したLPVsにLPV MPCを適用するという流れで，これをPVKO MPCと呼んでいます．さらに，Robust Controlの考え方によるRobust MPCが統合された内容となっており，その辺りについても簡単に紹介します．今回はMPCのRecursive feasibilityやStability等の理論的な内容が中心となっております．実装方法についてはあまり触れていませんのでご了承ください．また，Koopman作用素の部分に興味がある方は，前回のモデル化編かKoopman作用素やeDMDについての記事もあるので覗いてみてください．

PVKO-Based MPC

MPCでは，以下のような有限評価区間内の最適制御問題を評価区間を後退させながら解きます．

$$\begin{align} \min_{\bar{\bm y}{(\cdot)}, \bar{\bm u}{(\cdot)}}& \sum_{k=0}^{N-1}\left({\bm y}_{k \mid t}^{\top}{\bm Q}{\bm y}_{k \mid t}+{\bm u}_{k \mid t}^{\top}{\bm R}{\bm u}_{k \mid t}\right)+{\bm y}_{N \mid t}^{\top}{\bm P}{\bm y}_{N \mid t}\quad {\bm Q},~{\bm R},~{\bm P}\succ 0\tag{3a}\\ \text { s.t. } & \bar{\bm y}_{k+1 \mid t}={\bm A}\left(p_{k \mid t}\right)\bar{\bm y}_{k \mid t}+{\bm B}\left(p_{k \mid t}\right) \bar{\bm u}_{k \mid t},\quad k=0,~\cdots,~N-1\tag{3b}\\ &\bar{\bm y}_{0 \mid t}=\Psi_{\bm x}\left({\bm x}_{0 \mid t}\right)\tag{3c}\\ &{\bm C}\bar{\bm y}_{k \mid t} \in \mathbb{X} \ominus {\bm C} \mathbb{S},\quad k=0,~\cdots,~N-1 \tag{3d}\\ & \bar{\bm u}_{k \mid t} \in \mathbb{U} \ominus {\bm C} {\bm K} \mathbb{S},\quad k=0,~\cdots,~N-1 \tag{3e}\\ & \bar{\bm y}_{N \mid t} \in \mathbb{Y}_f \ominus \mathbb{S} \tag{3f} \end{align}$$

式$\text{(3a)}$は評価関数であり，初項がステージコスト，第2項がターミナルコストとなっています．式$\text{(3b)}$は状態予測モデルであり高次元空間におけるLPVs，式$\text{(3c)}$はその初期状態です．式$\text{(3d)},~\text{(3e)}$は状態と入力に関する制約を表し，式$\text{(3f)}$は終端制約を表しています．ここで，$\mathbb{S}$はRobust positively invariant setであり，ロバスト性を付加するために導入されています．この辺りに関しては少しごちゃごちゃしているのでまた後で言及します．Fig. 1はMPCのイメージです．現在の時刻を$t$とすると，$N$ステップ後までの$[t,~t+NT_s]$を有限評価区間とします．式$\text{(3)}$に添字として出てくる$k|t$は，時刻$t$から始まる評価区間内の$k$ステップ目を表しています．状態予測モデルに基づいて評価区間内における最適化の結果として$\bar{\bm u}^*{(\cdot)}$が得られるわけですが，MPCで実際に使う入力は$k=0$の値のみです．次の時刻の入力は，評価区間を$[t+T_s,~t+(N+1)T_s]$のように1ステップ後退させ，再度最適制御問題を解き同じように決定します．MPCでは，これの繰り返しにより逐次的に入力を決定します．

Fig. 1 MPC （$T_s$：サンプリング間隔）

MPCを設計するときに重要となるのが，Recursive feasibility と Stabilityです．Recursive feasibilityは制御の持続性を保証し，Stabilityは目標値 ${\bm y}=\bf 0$に収束することを保証します．これらは，MPCが上手く機能するために保証されるべき性質であり，ターミナルコストや終端制約によって保証することができます．次節では，状態予測モデルがLPVsでさらに外乱がある場合にこれらをどのように保証するのかを紹介します．また，以下にRecursive feasibility とそれに関わる用語の定義をのせておきます．必要のない人は読み飛ばしてください．

Recursive feasibility とは

Set of all feasible input sequence
Set of all feasible input sequenceとは，初期条件$\bar{\bm y}_{0 \mid t}$に対して定まる制約条件を満たす入力の集合であり，以下のように定義されます．

$$\mathcal{U}_N(\bar{\bm y}_{0 \mid t}):=\left\{\bar{\bm u}_{0 \mid t}, \cdots, \bar{\bm u}_{N-1 \mid t}\in \mathbb{U} \ominus C K \mathbb{S}:(\bar{\bm y}_{k \mid t}, \bar{\bm u}_{k \mid t}) \text { satisfies (3b)-(3f)}\right\} \tag{4}$$

つまり，$\mathcal{U}_N=\emptyset$は，現在の状態に対して制約条件を満たす入力がないということになり最適制御問題は解なしとなります．
Feasible set
Feasible setとは，$\mathcal{U}_N=\emptyset$でない初期状態の集合であり，以下のように定義されます．

$$\mathcal{X}_N:=\left\{\bar{\bm y}_{0 \mid t} \in \mathbb{Y}_f \ominus \mathbb{S}: \mathcal{U}_N(\bar{\bm y}_{0 \mid t}) \neq \emptyset\right\}\tag{5}$$

つまり，$\mathcal{X}_N$に含まれる状態から出発すれば最適制御問題の解が存在することが保証されます．しかし，あくまで現時刻の評価区間において保証されるのであり，次の評価区間内においても解が存在することを保証するものではありません．次の評価区間における初期状態がFeasible setから出ている可能性があるからです．そこで登場するのが，次のRecursive Feasibilityという概念です．

Recursive feasibility
時刻$t$で$\mathcal{X}_N$から出発しその後の未来においても Feasibilityが保たれる時，Recursivefeasibleであると言います．つまり，任意の時刻$t$において，

$$\bar{\bm y}_{0 \mid t}\in \mathcal{X}_N~\implies~ \bar{\bm y}_{0 \mid t+T_s} = {\bm A}\left(p_{0 \mid t}\right) \bar{\bm y}_{0 \mid t}+{\bm B}\left(p_{0 \mid t}\right) \bar{\bm u}^*_{0 \mid t}\in \mathcal{X}_N \tag{6}$$

であるときRecursive Feasibleとなります．

不確かさを考慮したRecursive feasibility と Stability の保証

不確かさのモデル化

現実の系には，外乱などのモデル化しきれない不確かさが存在します．Robust Controlとは，制御対象に不確かさがあったとしても，制御系がうまく機能するように設計する手法です．不確かさを含まないモデルをノミナルモデルと呼び，ここでは同定したPVKOにより記述される式$\text{(2a)}$にあたります．ノミナルモデルの状態と入力を$\bar{\cdot}$で表すとすると，

$$\begin{aligned} \bar{\bm y}_{k+1\mid t}&={\bm A}\left(p_{k\mid t}\right) \bar{\bm y}_{k\mid t}+{\bm B}\left(p_{k\mid t}\right)\bar{\bm u}_{k\mid t}\\ \end{aligned} \tag{7}$$

ノミナルモデルを用いて制御系を設計すると，現実との齟齬により思ったように性能が出ないことがあります．そこで，制御対象の不確かさを含めた以下のモデルを考えます．

$$\begin{aligned} {\bm y}_{k+1\mid t}={\bm A}\left(p_{k\mid t}\right){\bm y}_{k\mid t}&+{\bm B}\left(p_{k\mid t}\right) {\bm u}_{k\mid t}+{\bm w}_{k\mid t} \end{aligned} \tag{8}$$

これは，不確かさを全て${\bm w}_{k\mid t}$に押し込めた形になっています．ここで，式$\text{(8)}$の制御入力を以下とします．

$$\begin{aligned} {\bm u}_{k\mid t}=\bar{\bm u}_{k\mid t}+ {\bm K}({\bm y}_{k\mid t}-\bar{\bm y}_{k\mid t}) \end{aligned} \tag{9}$$

ここで，$\bar{\bm u}_{k\mid t}$は式$\text{(3)}$のノミナルモデルに基づく最適制御問題の解であり，${\bm K}$はフィードバックゲインです．誤差${\bm e}={\bm y}-\bar{\bm y}$のダイナミクスは，

$$\begin{aligned} {\bm e}_{k+1\mid t}={\bm A}^c\left(p_{k\mid t}\right){\bm e}_{k\mid t}+{\bm w}_{k\mid t}\quad \left({\bm A}^c\left(p_{k\mid t}\right)=\left({\bm A}\left(p_{k\mid t}\right)+{\bm B}\left(p_{k\mid t}\right){\bm K}\right)\right) \end{aligned} \tag{10}$$

この時間発展は${\bm K}$に依存し，これを上手く設定することでRobust positively invariant (RPI) set $\mathbb{S}$を求めることができます．

Robust positively invariant (RPI) setとは

$\Omega$が${\bm e}_{k+1}=\left({\bm A}\left(p_k\right)+{\bm B}\left(p_k\right){\bm K}\right) {\bm e}_k+{\bm w}_k$のRobust positively invariant (RPI) setであるとは，$\forall {\bm e}_k \in \Omega,$ $\forall p_k\in\mathbb{P},$ $\forall {\bm w}_k \in \mathbb{W}$に対して$\left({\bm A}\left(p_k\right)+{\bm B}\left(p_k\right) K\right) {\bm e}_k+{\bm w}_k\in\Omega$であることです．つまり，ある時刻で${\bm e}_k\in\Omega$であればその後の未来においても${\bm e}_k$は$\Omega$内に留まり続けます．ここで，positivelyは時間正方向の意味として使われています．

つまり，RPI setとは${\bm e}_{k\mid t}$がその内側に留まるように保証された集合のことで，

$$\begin{align} &{\bm C}{\bm y}_{k \mid t} \in \mathbb{X} ,\quad k=0,~\cdots,~N-1 \tag{11a}\\ & {\bm u}_{k \mid t} \in \mathbb{U} ,\quad k=0,~\cdots,~N-1 \tag{11b}\\ & {\bm y}_{N \mid t} \in \mathbb{Y}_f \tag{11c} \end{align}$$

といった式$\text{(8)}$に対する制約を，式$\text{(7)}$のノミナルモデルにおける制約として式$\text{(3d)}$から$\text{(3f)}$のように書き換えるために使われます．具体的には，式$\text{(3d)}$から$\text{(3f)}$の$\ominus$はPontryagin set differenceであり，$\mathbb{X},$ $\mathbb{U},$ $\mathbb{Y}_f$について考え得る誤差の影響の分だけ集合の外側を削っているイメージです．
式$\text{(10)}$の時間発展を書き下してみると，

$$\begin{align} {\bm e}_{0\mid t}&={\bf 0}\tag{12a}\\ {\bm e}_{1\mid t}&={\bm w}_{0\mid t}\tag{12b}\\ {\bm e}_{2\mid t}&={\bm A}^c\left(p_{1\mid t}\right){\bm e}_{1\mid t}+{\bm w}_{1\mid t}={\bm A}^c\left(p_{1\mid t}\right){\bm w}_{0\mid t}+{\bm w}_{1\mid t}\tag{12c}\\ {\bm e}_{3\mid t}&={\bm A}^c\left(p_{2\mid t}\right){\bm e}_{2\mid t}+{\bm w}_{2\mid t}={\bm A}^c\left(p_{2\mid t}\right){\bm A}^c\left(p_{1\mid t}\right){\bm w}_{0\mid t}+{\bm A}^c\left(p_{2\mid t}\right){\bm w}_{1\mid t}+{\bm w}_{2\mid t}\tag{12d}\\ \vdots~~&\notag\\ {\bm e}_{N\mid t}&={\bm A}^c\left(p_{N-1\mid t}\right)\cdots{\bm A}^c\left(p_{1\mid t}\right){\bm w}_{0\mid t}+\cdots+{\bm A}^c\left(p_{N-1\mid t}\right){\bm w}_{N-2\mid t}+{\bm w}_{N-1\mid t} \tag{12e} \end{align}$$

ここで，観測ノイズはないとして${\bm e}_{0\mid t}={\bf 0}$としました．つまり，RPI set $\mathbb{S}$は，

$$\begin{align} \mathbb{S}=\mathbb{W} & \oplus \operatorname{Conv}\left\{{\bm A}^c\left(p^i\right) \mathbb{W}, \forall i \in\{1,2, \ldots, l\}\right\} \notag\\ & \oplus \operatorname{Conv}\left\{{\bm A}^c\left(p^i\right) {\bm A}^c\left(p^j\right) \mathbb{W}, \forall i, j \in\{1,2, \ldots, l\}\right\}\tag{13}\\ &\oplus \cdots \notag \end{align}$$

より求めることができます．ここで$p^i~(i=1\cdots l)$は，式$\text{(2)}$の同定に用いるデータをサンプリングする際に設定されたパラメータ値です．詳しくは，モデル化編を参照してください．また，$\oplus$はMinkowski sumというもので，$\operatorname{Conv}\lbrace \cdot \rbrace$は$\lbrace \cdot \rbrace$を頂点とする凸包です．凸包を利用しているのは，${\bm A}^c\left(p_{k\mid t}\right)$が${\bm A}^c\left(p^i\right)$の間を線形補間することで得られているためです．このようにすることで，LPVsな系において外乱の影響を見積もることができます．式$\text{(13)}$の計算が発散しないためには，${\bm A}^c\left(p_{k \mid t}\right)$によって${\bm w}_{k\mid t}$が拡大していかないことが重要で，そうなるように${\bm K}$を設定します．つまり，

$$\begin{aligned} {\bm v}_{k+1\mid t}={\bm A}^c\left(p_{k\mid t}\right){\bm v}_{k\mid t} \end{aligned} \tag{14}$$

という系を考えたときに，

$$\begin{align} &\exists V({\bm v}_{k\mid t})={\bm v}_{k\mid t}^{\top}{\bm P}{\bm v}_{k\mid t}>0,~\forall {\bm v}_{k\mid t}\neq {\bf 0}\tag{15a}\\ &\text{such that}~ V({\bm v}_{k +1\mid t})-V({\bm v}_{k\mid t})\leq-\left({\bm v}_{k \mid t}^{\top}{\bm Q}{\bm v}_{k \mid t}+{\bm v}_{k \mid t}^{\top}{\bm K}^{\top}{\bm R}{\bm K}{\bm v}_{k \mid t}\right) \tag{15b} \end{align}$$

のような2次形式のリアプノフ関数が存在するように${\bm K}$を設定します．さらに，式$\text{(15b)}$について時間方向に和をとり，$V({\bm v}_{N\mid t})\geq0$を使うと，

$$\begin{align} V({\bm v}_{0\mid t})\geq\sum_{k=0}^{N-1}\left({\bm v}_{k \mid t}^{\top}{\bm Q}{\bm v}_{k \mid t}+{\bm v}_{k \mid t}^{\top}{\bm K}^{\top}{\bm R}{\bm K}{\bm v}_{k \mid t}\right) \tag{16} \end{align}$$

つまり，$V({\bm v}_{0\mid t})$で抑えられることが分かります．式$\text{(3d)}$から$\text{(3f)}$より$\mathbb{S}$が大きくなることはノミナルモデルにおける制約条件が厳しくなることを意味するので，$\mathbb{S}$は小さい方が望ましいです．そこで，以下のような最適化問題を通して${\bm K}$を決定します．

$$\begin{align} \min _{{\bm P}, {\bm K}} &V({\bm v}_{0\mid t})={\bm v}_{0 \mid t}^{\top}{\bm P}{\bm v}_{0 \mid t} \tag{17a}\\ \text { s.t. } &{\bm P}\succ 0\tag{17b}\\ &~{\bm A}^c(p^i)^{\top} {\bm P} {\bm A}^c(p^i)- {\bm P}\preceq- {\bm Q}- {\bm K}^{\top} {\bm R} {\bm K},\quad \text{for}~i=1,~2,~\cdots,~l\tag{17c} \end{align}$$

ここで，式$\text{(17c)}$は式$\text{(15b)}$を式$\text{(14)}$と$\text{(15a)}$に基づいて書き換えたものです．最適化問題について全ての${\bm v}_{0 \mid t}$について最小化する代わりに，

$$\begin{align} E[{\bm v}_{0 \mid t}]={\bf 0},\quad E[{\bm v}_{0 \mid t}{\bm v}_{0 \mid t}^{\top} ]={\bf I} \tag{18} \end{align}$$

を仮定し，$E[V({\bm v}_{0\mid t})]$を最小にする問題を考えます．

$$\begin{align} &V({\bm v}_{0\mid t})=\operatorname{tr}\left( {\bm v}_{0 \mid t}{\bm v}_{0 \mid t}^{\top}{\bm P}\right)\tag{19} \end{align}$$

より，

$$\begin{align} &E[V({\bm v}_{0\mid t})]=E\left[\operatorname{tr}\left( {\bm v}_{0 \mid t}{\bm v}_{0 \mid t}^{\top}{\bm P}\right)\right]=\operatorname{tr}\left\{E[ {\bm v}_{0 \mid t}{\bm v}_{0 \mid t}^{\top}{\bm P}]\right\}=\operatorname{tr}({\bm P}) \tag{20} \end{align}$$

よって，最適化問題は，

$$\begin{align} \min _{{\bm P}, {\bm K}} &~\operatorname{tr}({\bm P}) \tag{21}\\ \text { s.t. } &\text{(14b), (14c)} \notag \end{align}$$

以上で，${\bm K,~ \bm P},~\mathbb{S}$が求まったので，これらを用いてRecursive feasibility と Stabilityの保証について言及していきます．

Recursive Feasibility の保証

現時刻の状態においてfeasible input sequenceが存在するとき，次の時刻でもfeasible input sequenceの存在を保証する方法について説明します．
現時刻を$t$とすると，その時刻の状態におけるFeasibilityより式$\text{(3)}$の最適制御問題の解候補が存在します．その内の最適解を以下とします．

$$\begin{align} \bar{\bm U}^*_t&=[\bar{\bm u}^*_{0 \mid t},~\bar{\bm u}^*_{1 \mid t},~\cdots,~\bar{\bm u}^*_{N-1 \mid t}] \tag{22a}\\ \bar{\bm Y}^*_t&=[\bar{\bm y}^*_{0 \mid t},~\bar{\bm y}^*_{1 \mid t},~\cdots,~\bar{\bm y}^*_{N-1 \mid t},~\bar{\bm y}^*_{N \mid t}] \tag{22b} \end{align}$$

Feasibilityが保たれるためには，次の評価区間においても実行可能解が存在していれば良いわけです．そこで，次の時刻の制御則として，

$$\begin{align} \bar{\bm U}_{t+T_s}&=[\bar{\bm u}^*_{1 \mid t},~\bar{\bm u}^*_{2 \mid t},~\cdots,~\bar{\bm u}^*_{N-1 \mid t},~{\bm K}\bar{\bm y}^*_{N \mid t}] \tag{23} \end{align}$$

を考えてみます．ここで，$\bar{\bm u}^*_{k \mid t}$ $(k=1,~\cdots,~N-1)$は先の区間の実行可能解なので式$\text{(3e)}$を既に満たしており，

$$\begin{align} \bar{\bm Y}_{t+T_s}&=[\bar{\bm y}^*_{1 \mid t},~\bar{\bm y}^*_{2 \mid t},~\cdots,~\bar{\bm y}^*_{N \mid t},~{\bm A}^cp_{N-1 \mid t+T_s}\bar{\bm y}^*_{N \mid t}] \tag{24} \end{align}$$

についても，$\bar{\bm y}^*_{k \mid t}$ $(k=1,~\cdots,~N-1)$は，式$\text{(3d)}$を既に満たしています．後は，

$$\begin{align} {\bm K}\bar{\bm y}^*_{N \mid t}&\in \mathbb{U} \ominus {\bm C} {\bm K} \mathbb{S} \tag{25a}\\ {\bm C}\bar{\bm y}^*_{N \mid t}&\in \mathbb{X} \ominus {\bm C} \mathbb{S} \tag{25b}\\ {\bm A}^cp_{N-1 \mid t+T_s}\bar{\bm y}^*_{N \mid t} &\in \mathbb{Y}_f \ominus \mathbb{S} \tag{25c} \end{align}$$

が満たされれば，式$\text{(23)}$が実行可能解（最適解とは限らない）であることが言えます．そこで，局所的な制御則 ${\bm K}\bar{\bm y}^*_{N \mid t}$に対応させて，$\mathbb{Y}_f$を${\bm C}\mathbb{Y}_f\subseteq\mathbb{X},~{\bm C}{\bm K}\mathbb{Y}_f\subseteq\mathbb{U}$を満たすような

$$\begin{aligned} {\bm y}_{k+1\mid t}={\bm A}^c\left(p_{k\mid t}\right){\bm y}_{k\mid t}+{\bm w}_{k\mid t} \end{aligned} \tag{26}$$

のRPI setとします．すると，$\mathbb{Y}_f$から出発した状態はその内部に留まるので，

$$\begin{align} \bar{\bm y}_{N \mid t}\in \mathbb{Y}_f~\implies~~\bar{\bm y}_{N+1 \mid t}\in \mathbb{Y}_f,~\forall t\in\mathbb{N}^+ \tag{27} \end{align}$$

より式$\text{(25)}$が満たされるので，式$\text{(23)}$が実行可能解となりRecursive Feasibilityが保証されました．

Stability の保証

ターミナルコストと先ほどの局所的な制御則 ${\bm K}\bar{\bm y}^*_{N \mid t}$を用いて，MPCが漸近安定であることを保証します．
現時刻$~t$における評価関数を，

$$\begin{align} J_t=\sum_{k=0}^{N-1}\left(\bar{\bm y}_{k \mid t}^{\top}{\bm Q}\bar{\bm y}_{k \mid t}+\bar{\bm u}_{k \mid t}^{\top}{\bm R}\bar{\bm u}_{k \mid t}\right)+\bar{\bm y}_{N \mid t}^{\top}{\bm P}\bar{\bm y}_{N \mid t}\tag{28} \end{align}$$

として，最適解である式$\text{(22)}$に対する評価関数を$J_t^*$ とします．式$\text{(23)}$の制御則とそれによって時間発展した状態である式$\text{(24)}$のもとで，次の評価区間における評価関数$~J_{t+T_s}$は，

$$\begin{align} J_{t+T_s}&=J_t^*-{\bar{\bm y}^*_{N \mid t}}^{\top}{\bm P}\bar{\bm y}^*_{N \mid t}-\left({\bar{\bm y}^*_{0 \mid t}}^{\top}{\bm Q}\bar{\bm y}^*_{0 \mid t}+{\bar{\bm u}^*_{0 \mid t}}^{\top}{\bm R}\bar{\bm u}^*_{0 \mid t}\right)+\left({\bar{\bm y}^*_{N \mid t}}^{\top}{\bm Q}\bar{\bm y}^*_{N \mid t}+{{\bar{\bm y}^*_{N \mid t}}^{\top}{\bm K}}^{\top}{\bm R}{\bm K}\bar{\bm y}^*_{N \mid t}\right)+\bar{\bm y}_{N+1 \mid t}^{\top}{\bm P}\bar{\bm y}_{N+1 \mid t}\notag\\ &\leq J_t^*-{\bar{\bm y}^*_{N \mid t}}^{\top}{\bm P}\bar{\bm y}^*_{N \mid t}+\left({\bar{\bm y}^*_{N \mid t}}^{\top}{\bm Q}\bar{\bm y}^*_{N \mid t}+{{\bar{\bm y}^*_{N \mid t}}^{\top}{\bm K}}^{\top}{\bm R}{\bm K}\bar{\bm y}^*_{N \mid t}\right)+{\bar{\bm y}^*_{N \mid t}}^{\top}{\bm A}^c\left(p_{N-1 \mid t+1}\right)^{\top}{\bm P}{\bm A}^c\left(p_{N-1 \mid t+1}\right)\bar{\bm y}^*_{N \mid t}\notag\\ &= J_t^*+{\bar{\bm y}^*_{N \mid t}}^{\top}\lbrace{{\bm A}^c\left(p_{N-1 \mid t+1}\right)^{\top}{\bm P}{\bm A}^c\left(p_{N-1 \mid t+1}\right)-\bm P+\bm Q+{\bm K}^{\top}{\bm R}{\bm K}} \rbrace\bar{\bm y}^*_{N \mid t}\notag\\ &\leq J_t^* \tag{29} \end{align}$$

ここで，式$\text{(17c)}$を使いました．よって，$J_{t+T_s}^* \leq J_{t+T_s}\leq J_t^*$であるので，$t\rightarrow\infty$で式$\text{(7)}$のノミナルモデルによる時間発展が原点に収束することを保証することができます．

以上により，Recursive feasibilityやStabilityが保証され，MPCが上手く機能することが期待されます．次に以上の制御則に基づいたシミュレーション結果を示します．

制御性能の評価

対象とするNPVsとして，以下のVan der Pol方程式を考えます．

$$\begin{align} & \dot{x}=2y\tag{30a} \\ & \dot{y}=-0.8x+p(y-2x^2y)+u\tag{30b} \end{align}$$

Fig. 2(b)のようなパラメータ$p$のもとで$u$をランダムウォークモデルに従わせた時のサンプリングデータに基づいて，${\bm A}\left(p_k\right),~{\bm B}\left(p_k\right)$を推定します．制御系としては，このPVKOを状態予測モデルとして用いるPVKO-MPCと，Parameter-Varying でないKoopman 作用素を用いるKO-MPCおよび式$\text{(30)}$のNPVsを用いるNMPCを用意し，その性能を比較します．以下，それぞれの制御系で用いる状態予測モデルの推定について箇条書きにします．

• PVKO-MPC
  • サンプリングの際のパラメータ設定：$p^i= 1,~2,~3,~4,~5~~(l=5)$
  • データの時刻数：各$p^i$ごとに$1000s$のデータを$0.01s$間隔でサンプリングし全部で$5\times10^5$時刻
  • 基底関数 (radial basis function)の数：$\Psi=\left[x, y, x y, x^2, y^2, x^2 y, x y^2, x^3, y^3\right]^{\top}$からなる9個
• KO-MPC
  • データの時刻数: $5000s$のデータを$0.01s$でサンプリングし$5\times10^5$時刻
  • 基底関数 (radial basis function)の数：$\Psi=\left[x, y, x y, x^2, y^2, x^2 y, x y^2, x^3, y^3\right]^{\top}$からなる9個
• NMPC
  • 式$\text{(30)}$を，$0.01s$の間隔でオイラー法により離散化したもの

Fig. 2に，それぞれの制御結果を示します．Fig. 2(a)は状態の時間変化で，黒線は無限時間評価区間のNMPCの結果を表しています．Fig. 2(c)は制御入力$u$，Fig. 2(d)は以下の累積コストを示しています．

$$\begin{align} J_c(k)=\sum_{i=0}^k\left({\bm x}_{i}^{\top}{\bm C}{\bm Q}{\bm C}^{\top}{\bm x}_{i}+{\bm u}_{i}^{\top}{\bm R}{\bm u}_{i}\right) \tag{28} \end{align}$$

Tab.1 は，平均計算時間と累積コストおよびその無限時間評価区間のNMPCの結果に対する相対誤差を示しています．Koopman 作用素を用いたKO-MPCとPVKO-MPCでは，NMPCに対して計算時間が短いことが分かります．また，累積コストで比較すると，PVKO-MPCがKO-MPCに比べてNMPCの結果に近いことが分かります．また，NMPCは3つのMPCの中で唯一，式$\text{(30)}$を使って状態予測モデルを立てています．よって，PVKO-MPCはKO-MPCやNMPCの中で比較的計算コストが低く，さらには正確な状態予測モデルを使った制御系に近い結果を示していることが分かりました．

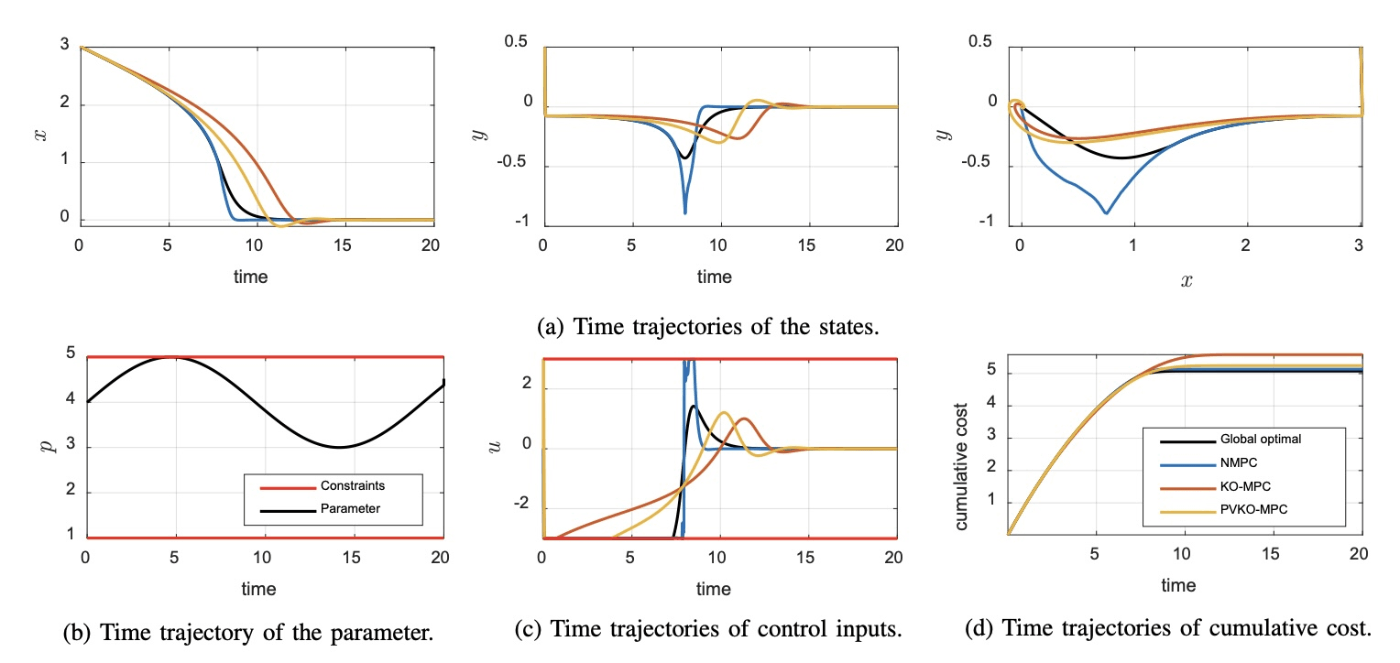
Fig. 2 制御結果 (出典：Lee et al. (2023))

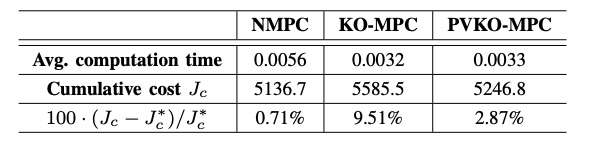
Tab.1 制御結果 (出典：Lee et al. (2023))

参考文献

Lee, Changyu, Kiyong Park and Jinwhan Kim. “Parameter-Varying Koopman Operator for Nonlinear System Modeling and Control.” 2023 62nd IEEE Conference on Decision and Control (CDC) (2023): 3700-3705.