拡張動的モード分解 eDMD について

当記事は東京工業大学の藤井成美（https://www.linkedin.com/in/narumi-fujii-32304330b/ ）によって執筆されました

はじめに

本記事では，IEEE Transactions on Roboticsにおいて2021年に発表された“Data-Driven Control of Soft Robots Using Koopman Operator Theory”という論文[1]を参考にeDMDについて紹介します．対象とする系は，Fig. 1に示す空気圧式人工筋肉(PAMs)というソフトロボットで，自由度の高さからモデル化が課題となっています．論文では，Koopman作用素理論に基づくeDMDを用いたモデル化およびそのモデルに基づくMPCの結果が示されています．本記事では，eDMDに関係しているモデル化とその精度評価の部分について中心的に説明します．

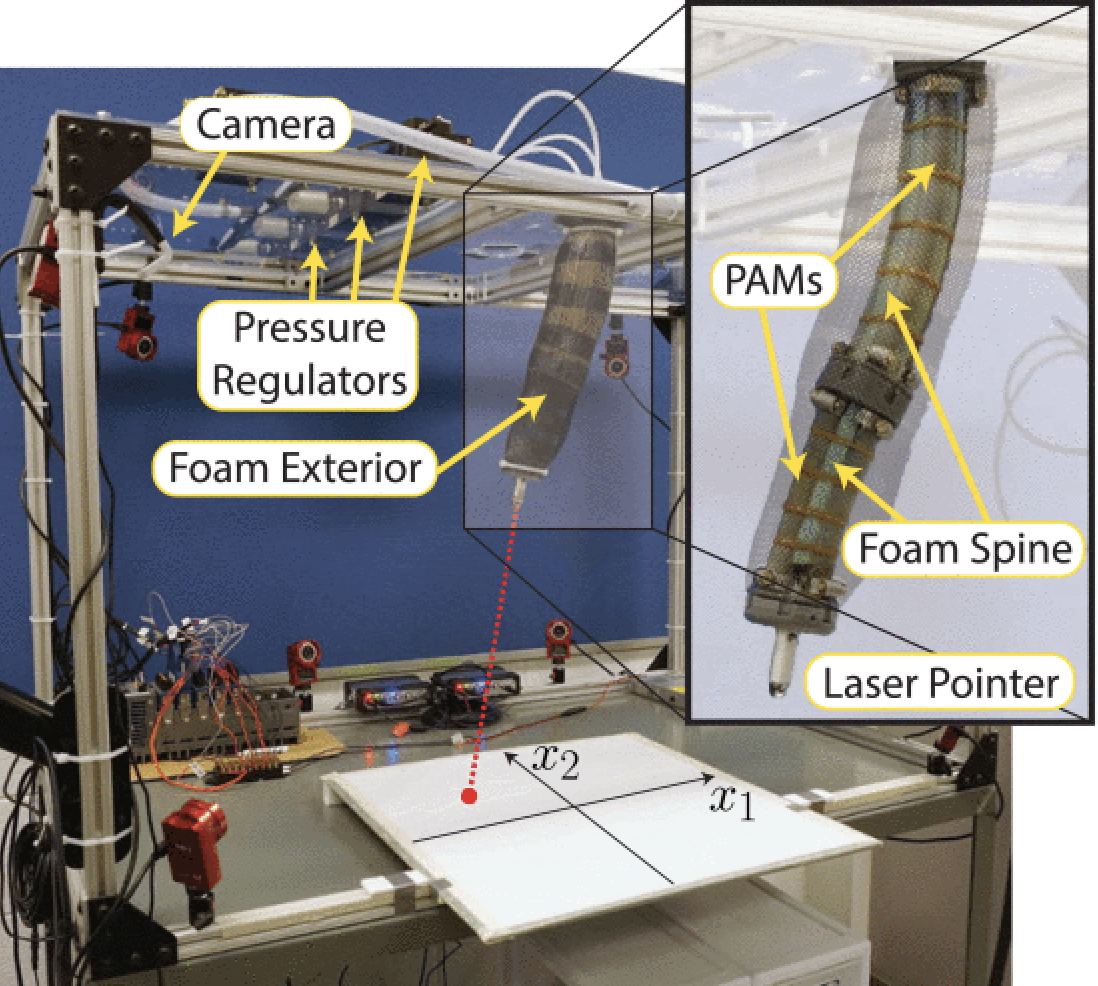
Fig. 1 対象のソフトロボット[1]：先端にレーザポインタがついており，下の平面に当たるようになっています．

DMDとeDMD

eDMDは，extended DMDの略でDMDを拡張した手法です．DMDは，Data-Driven型のアプローチに基づいて，系を離散時間線形系としてモデル化する手法です．例として以下の系を考えます．

$$\begin{align} \dot{\bm x}(t) = {\bm F} ({\bm x}(t)) \tag{1} \end{align}$$

ここで，${\bm x}(t)\in \mathcal{X} \subset \mathbb{R}^n$であり，${\bm F}:\mathbb{R}^n\rightarrow\mathbb{R}^n$は一般に非線形です．DMDでは，(1)の系から得られた離散時間データ${\bm x}_k:={\bm x}(t_k)$について，以下の線形写像${\bm A}\in\mathbb{R}^{n\times n}$を得ることを目的とします．

$$\begin{align} {\bm x}_{k+1}={\bm A}{\bm x}_k t_{k+1}=t_k+T \tag{2} \end{align}$$

ここで，$T$はデータのサンプリング周期です．${\bm A}$は，膨大な数の時空間データから尤もらしいものとして同定されます． つまり，$k=0,~1,\cdots,~K-1$のデータ行列${\bm X_a}$と1ステップシフトしたデータ行列${\bm X_b}$より，

$$\begin{align} {\bm X}_a=\left[\begin{array}{cccc} \mid & \mid & & \mid \\ {\bm x}_0 & {\bm x}_1 & \cdots & {\bm x}_{K-1} \\ \mid & \mid & & \mid \end{array}\right], ~~~{\bm X}_b=\left[\begin{array}{cccc} \mid & \mid & & \mid \\ {\bm x}_1 & {\bm x}_2 & \cdots & {\bm x}_{K} \\ \mid & \mid & & \mid \end{array}\right] \tag{3a} \end{align}$$

$$\begin{align} {\bm X}_b&\simeq{\bm A}{\bm X}_a \tag{3b}\\ {\bm A}&={\bm X}_b{\bm X}_a^{\dagger} \tag{3c} \end{align}$$

式(1)を知らなくても，データがあれば実装できることが利点です．
　しかし，式(1)が非線形性を含む場合，式(2)でうまく表せない場合があります．特に，系の次元が低い時はあまりうまくいかず，DMDに代わってeDMDが使われます．参考[2]では，式(1)のような非線形系が等価な無限次元の線形表現を有し，その無限次元線形作用素はKoopman作用素と呼ばれていることが紹介されています．次元の拡張には，状態を引数とするスカラー値の観測関数([2]では，エンコード関数)が用いられ，Koopman作用素は観測関数の時間発展を記述します．無限次元のKoopman作用素を扱うことは数値的に不可能なので，有限次元における近似的なKoopman作用素(有限次元なので行列)として同定します．その際に使われる手法がeDMDです．DMDが状態の離散時間線形系を同定するのに対し，eDMDは次元が拡張された空間における観測関数の離散時間線形系を同定します．

Koopman作用素理論に基づくeDMDを用いたモデルの構築

Koopman作用素は観測関数に作用して時間発展を記述します．全ての(一般に非線形な)観測関数$f:\mathbb{R}^n\rightarrow\mathbb{R}$を含む空間を$\mathcal{F}$とすると，ある観測関数$f\in \mathcal{F}$と式(1)の流れ$\phi _t$^[1]$:\mathbb{R}^n\rightarrow\mathbb{R}^n$が与えられた時，Koopman作用素$U_t:\mathcal{F}\rightarrow\mathcal{F}$は以下で定義されます．

$$\begin{align} U_t f = f \circ \phi _t \tag{4} \end{align}$$

Koopman作用素が観測関数を時間発展させていることをより明示的に書くのであれば，以下のようになります^[2]．

$$\begin{align} U_{T} f^{t_k} = f^{t_k} \circ \phi _{T} =f^{t_{k+1}} \tag{5} \end{align}$$

ここで，$f^{t_{k}}$は時刻$t_k$における観測関数です．流れ$\phi _t$は一般に非線形写像ですが，Koopman作用素$U_t$は線形作用素です．
　eDMDを用いて，Koopman作用素の有限次元近似$\bar{U}_T$を同定します(ここでは，有限次元の近似値に$\bar{}$を用います)．$\bar{\mathcal{F}}\subset\mathcal{F}$を$N(>n)$個の基底関数$\psi _i: \mathbb{R}^n\rightarrow \mathbb{R}$で張られる空間とします．基底関数の最初の$n$個は状態そのものを用います．結果として，後の式(17)のように$\bar{\mathcal{F}}$から元の状態空間に戻す写像が簡単になります．つまり，

$$\begin{align} {\bm \psi} ({\bm x}) &:= \begin{bmatrix} \psi_1({\bm x}),~\psi_2({\bm x}),~\cdots,~\psi_N({\bm x})\end{bmatrix}^\top = \begin{bmatrix}x_i & \cdots & x_n & \psi _{n+1} ({\bm x}) & \cdots & \psi _N ({\bm x}) \end{bmatrix}^\top \tag{6} \end{align}$$

ここで，$x_i$は${\bm x}$の$i$番目の要素です．モデルの精度は基底の選び方に依存し^[3]，基底関数はヒューリスティックに決定する必要があります．任意の観測関数$\bar{f}^{t_k}\in\bar{\mathcal{F}}$は，基底関数の線型結合で表され，

$$\begin{align} \bar{f}^{t_k}({\bm x}_k) ={{\bm \theta}^{t_k}} ^\top{\bm \psi} ({\bm x}_k) \tag{7} \end{align}$$

ここで，${\bm \theta}^{t_k}:=\left[\theta_1^{t_k} \cdots \theta_N^{t_k}\right]^{\top}\in\mathbb{R}^N$は，観測関数のベクトル表現です．ベクトル表現を導入することで，$\bar{\mathcal{F}}$上の線形作用$\bar{U}_T$を行列$\bar{\bm U}_T\in\mathbb{R}^{N\times N}$で表現することができます．つまり，式(5)の近似的なベクトル表現として以下を得ることができます．

$$\begin{align} \bar{\bm U}_{T} {\bm \theta}^{t_k} = {\bm \theta}^{t_{k+1}} \tag{8} \end{align}$$

よって，式(4)の(離散時間)有限次元近似は，

$$\begin{align} \bar{U}_{T} \bar{f}^{t_k}({\bm x}_k) = \bar{f}^{t_k} \circ \phi _{T} ({\bm x}_k) \tag{9} \end{align}$$

ここで，

$$\begin{align} \bar{U}_T \bar{f}^{t_k}({\bm x_k})=\bar{f}^{t_{k+1}}({\bm x_k})={{\bm \theta}^{t_{k+1}}} ^\top{\bm \psi} ({\bm x_k}) =\left(\bar{\bm U}_{T} {\bm \theta}^{t_k}\right)^\top{\bm \psi} ({\bm x_k}) \tag{10} \end{align}$$

より，

$$\begin{align} \left(\bar{\bm U}_{T} {\bm \theta}^{t_k}\right)^\top{\bm \psi} ({\bm x_k}) &= {{\bm \theta}^{t_k}}^\top {\bm \psi} \circ \phi _{T}({\bm x_k}) \tag{11a} \end{align}$$

全ての，${\bm \theta}^{t_k}$について成り立つので，

$$\begin{align} \bar{\bm U}_{T}^\top {\bm \psi} ({\bm x_k}) &= {\bm \psi} \circ \phi _{T}({\bm x_k}) \tag{11b}\\ \bar{\bm U}_{T} &= \left({\bm \psi}^\top ({\bm x_k}) \right)^\dagger ({\bm \psi} \circ \phi _{T}({\bm x_k}))^\top \tag{11c} \end{align}$$

$\bar{\bm U}_T$を同定するために，式(3a)のように$\mathcal{F}$上の時空間データセットを作ります．

$$\begin{align} &{\bm \Psi} _a := \begin{bmatrix}{\bm \psi} ({\bm x}_0)^\top \\ \vdots \\ {\bm \psi}({\bm x}_{K-1})^\top \end{bmatrix} ,~~~{\bm \Psi} _b := \begin{bmatrix}{\bm \psi} ({\bm x}_1)^\top \\ \vdots \\ {\bm \psi}({\bm x}_{K})^\top \end{bmatrix} \tag{12} \end{align}$$

ここで，${\bm \psi}({\bm x}_{k+1})={\bm \psi} \circ \phi _{T}({\bm x_k})$を用いました．式(11c)は各時刻で成り立つはずなので，

$$\begin{align} \bar{\bm U}_{T} &:= {\bm \Psi} _a^\dagger {\bm \Psi} _b \tag{13} \end{align}$$

これは，DMDの式(3c)に類似しています．次に以上の議論を用いて，制御入力を含む離散時間線形系

$$\begin{align} {\bm z}_{k+1} &= {\bm A} {\bm z}_k + {\bm B} {\bm u}_k \tag{14a}\\ {\bm x}_k &= {\bm C} {\bm z}_k \tag{14b} \end{align}$$

を同定します．ここで，${\bm z}_{0}= {\bm \psi} ({\bm x}_0)\in\mathbb{R}^N,~{\bm u}_k={\bm u}(t_k)\in\mathbb{R}^m$は制御入力です．モデル構築の方法は，式(12)のデータセットに制御入力を追加し先程と同様に，

$$\begin{align} &{\bm \Gamma} _a := \begin{bmatrix} {\bm \psi} ({\bm x}_0)^\top ~{\bm u}_0^\top\\ \vdots \\ {\bm \psi}({\bm x}_{K-1})^\top ~{\bm u}_{K-1}^\top \end{bmatrix} ,~~~{\bm \Gamma} _b := \begin{bmatrix} {\bm \psi} ({\bm x}_1)^\top ~{\bm u}_0^\top\\ \vdots \\ {\bm \psi}({\bm x}_{K})^\top ~{\bm u}_{K-1}^\top \end{bmatrix} \tag{15a}\\ &\bar{\bm U}_{T} := {\bm \Gamma} _{a }^\dagger {\bm \Gamma} _b \tag{15b} \end{align}$$

ここで，$\bar{\bm U}_{T}\in\mathbb{R}^{(N+m)\times(N+m)}$であり，式(14a)との対応関係を考えると，

$$\begin{align} \bar{\bm U}_{T} = \begin{bmatrix}{\bm A}_{N \times N} & {\bm B}_{N \times m} \\ {\bm O}_{m \times N} & {\bm I}_{m \times m} \end{bmatrix} \tag{16} \end{align}$$

また，基底関数を式(6)のように定めたので，状態空間への写像${\bm C}\in\mathbb{R}^{n\times N}$は，

$$\begin{align} {\bm C} = \begin{bmatrix}{\bm I}_{n \times n} & {\bm O}_{n \times (N-n)} \end{bmatrix} \tag{17} \end{align}$$

以上で，式(14a), (14b)として系を同定できたので，MPCによる制御設計の適用ができます(Fig. 2)．しかし，式(14a)における写像は，${\bm z}_{k}$を${\bm \psi}$の像$\mathcal{M}$上に写像しない場合があります(Fig. 3)．これは，予測の精度を落とすため各時刻において$\mathcal{M}$からの距離が小さくなるように修正します．$\mathcal{M}$上へ修正するための写像${\bm P}$は，理想的には以下を満たします．

$$\begin{align} {\bm P} \left({\bm A} {\bm \psi}({\bm x}_k) + {\bm B} {\bm u}_k \right) &= {\bm \psi} ({\bm x}_{k+1}) \tag{18} \end{align}$$

つまり，${\bm A} {\bm \psi}({\bm x}_k) + {\bm B} {\bm u}_k \notin\mathcal{M}$であったとしても，${\bm P} \left({\bm A} {\bm \psi}({\bm x}_k) + {\bm B} {\bm u}_k \right)\in\mathcal{M}$となるように写像します．${\bm P}$は，以下のデータセットから求められます．

$$\begin{align} &{\bm \Omega} _a := \begin{bmatrix}\left({\bm A} {\bm \psi}({\bm x}_0) + {\bm B} {\bm u}_0 \right)^\top \\ \vdots \\ \left({\bm A} {\bm \psi}({\bm x}_{K-1}) + {\bm B} {\bm u}_{K-1} \right)^\top \end{bmatrix} \tag{19a} \\ &{\bm P} := \left({\bm \Omega} _{a}^\dagger {\bm \Psi} _b \right)^\top \tag{19b} \end{align}$$

よって，修正された時間発展は以下のようになります．

$$\begin{align} {\bm z}_{k+1} &= \hat{{\bm A}} {\bm z}_k + \hat{{\bm B}} {\bm u}_k \tag{20} \end{align}$$

ここで，$\hat{{\bm A}}:={\bm P}{\bm A},~\hat{{\bm B}}:={\bm P}{\bm B}$です．論文内では，Koopman作用素を用いて非線形系を同定する方法も記述されていますが，ここでは省略します．

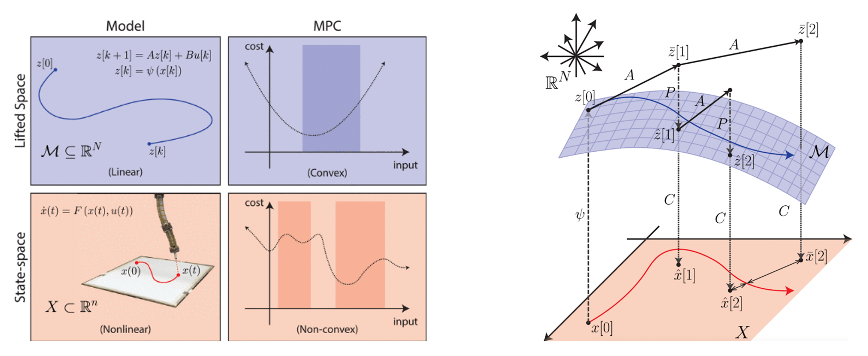
Fig. 2 モデルの構築とMPCの適用[1]　　　　　　　　　　　　Fig. 3 ${\bm P}$による$\mathcal{M}$付近への状態の修正[1]

予測精度の評価

実験内容

Fig. 1に示したソフトロボットについて，レーザポインタの示す位置${\bm x}=[x_1 x_2]^\top\in \mathbb{R}^2$を状態としある正弦波入力${\bm u}\in \mathbb{R}^3$を加えます．${\bm x}$について実機の結果${\bm x}^a$とモデルから予測される結果${\bm x}^p$を比較し，モデルの精度を評価します．各時刻の誤差を$\lVert{\bm x}^p-{\bm x}^a\rVert$とし，原点と実機が示すポインタ間の距離$\lVert{\bm x}^a\rVert$を用いて正規化されています．
　ここでは，他の同定方法を用いたモデルを3つ用意し，計4つのモデルの予測精度を比較します．

• Koopman(linear): 式(20)で同定されたモデル
  • データの時刻数: $K=45103$
  • 基底関数(最大次数2の単項式)の数: $N=36$
• State Space: サブスペース法[3]を用いた線形状態空間モデル
• Koopman(nonlinear): 非線形Koopmanモデル(本記事では省略しました)
  • データの時刻数: $K=45103$
  • 基底関数(最大次数3の単項式)の数: $N=35$
• Neural Network: Levenberg-Marquardt逆伝搬法による入力ありの非線形自己回帰ニューラルネットワークモデル
  • データの時刻数: $K=45103$
  • 隠れニューロンの数: $10$

結果

Fig. 4に示されるように，線形系で比較するとKoopman(linear)モデルはState Spaceモデルよりも良い予測を与えています．非線形系も含めて比較すると，Koopman(nonlinear)モデルが最も高い予測精度を有しており，次いでKoopman(linear)モデル，そしてNeural Networkモデル最後にState Spaceモデルとなっています．

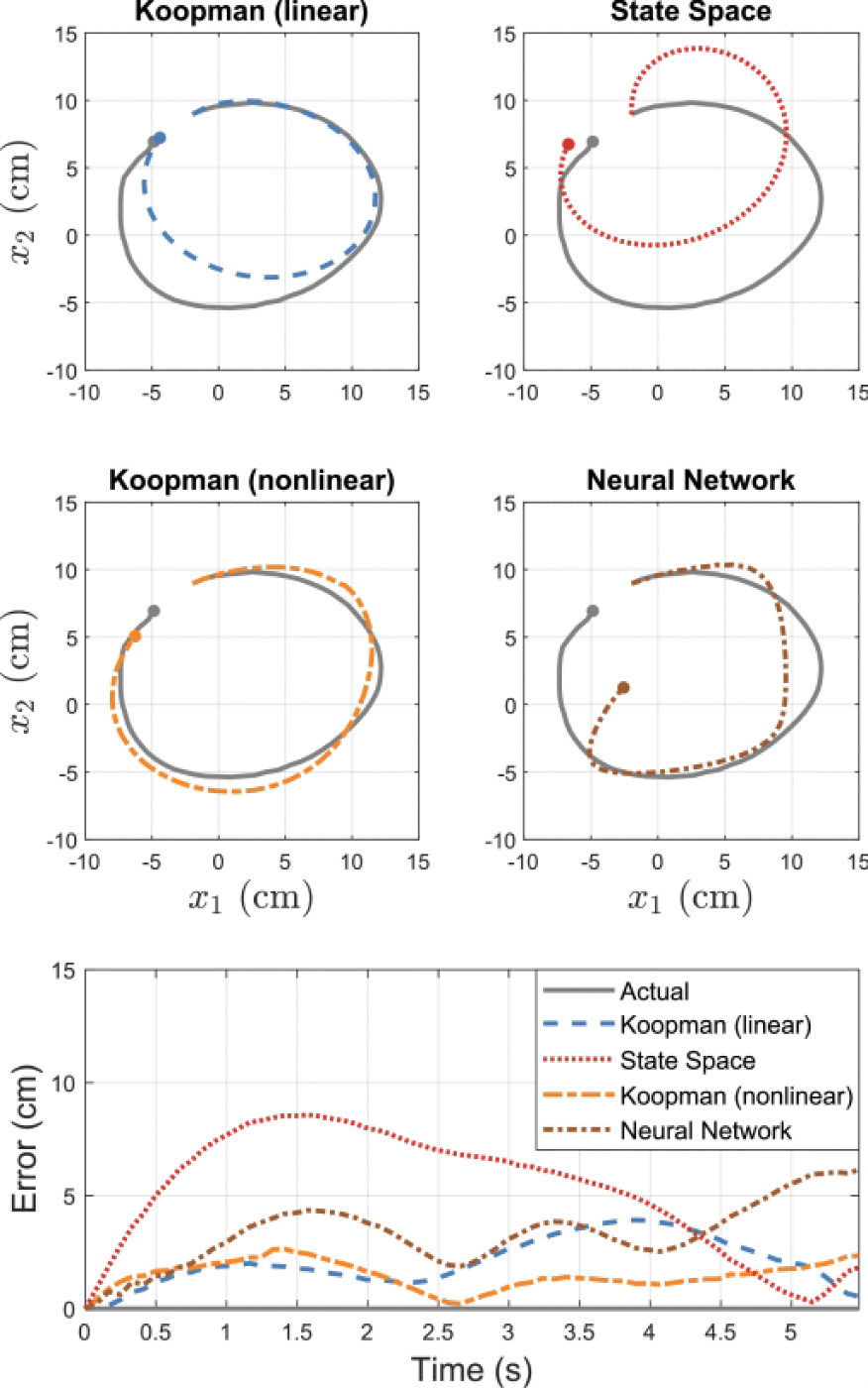
Fig. 4 モデルの予測結果[1]

最後に

この記事では深く言及しませんが，論文内では同定したモデルを用いたMPCの実機への適用結果も示されています．Koopman(linear)モデルに基づいたMPCは，Koopman(nonlinear)モデルに基づくMPCよりも計算コストが小さく，目標軌道との誤差のオーダーはいずれもソフトロボティクス固有の応答変動のオーダーと同じであり十分な制御性能が示されています．また，[1]の研究グループのmatlabソースコードをpythonソースコードに書き換えたものを公開していますので，実装の参考にしてください(link)．
　また，本記事の執筆にあたり文献[4]も参考にいたしました．

参考文献

[1] D. Bruder, X. Fu, R. B. Gillespie, C. D. Remy and R. Vasudevan, “Data-Driven Control of Soft Robots Using Koopman Operator Theory," in IEEE Transactions on Robotics, vol. 37, no. 3, pp. 948-961, June 2021, doi:10.1109/TRO.2020.3038693.
[2] 株式会社 Proxima Technology. “クープマン作用素理論×ディープラーニング×非線形制御”. Zenn. 2023-12. https://zenn.dev/takuya_fukatsu/articles/00cee74c25cd4a, （参照 2024-05-17）．
[3] P. Van Overschee and B. De Moor. Subspace Identification for Linear Systems: Theory Implementation Applications. Berlin, Germany:Springer, 2012.
[4] J. Nathan Kutz, Steven L. Brunton, Bingni W. Brunton, and Joshua L. Proctor. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, 2016.

脚注

1. 式(1)において，初期条件${\bm x}_0$とした時の時刻$t$の解．

2. 表記を簡単にするために離散時間的に書いていますが，式(3a)のようなデータセットを考えていると思ってください．

3. ${\bm \psi}_i$の像$\mathcal{M}$は，各基底関数$\psi _i$の像$\mathcal{R}_i$の直積となり，同定した$\bar{U}_t$による時間発展が$\mathcal{M}$上に乗らない場合予測精度が悪くなります．論文では，その対処方法も提示されています(式(18)辺り)．