Zenn
🎃

クープマン作用素理論×ディープラーニング×非線形制御

2023/12/23に公開
AI
機械学習
制御工学
tech

KOT（Koopman Operator Theory）とは？

KOT（Koopman Operator Theory）は非線形なシステムに従う実験データ（制御状態、制御入力）を非線形な関数（エンコード関数）によって高次元空間へ写像することで、その高次元空間上では線形なオペレータ（クープマンオペレータ）に従い状態が変化していくと仮定する方法です。
発想としてはカーネル法に近いイメージになるかもしれません。

この方法で、ソフトロボット分野で今までのLSTMのモデリング以上に正確で高速にモデリング＋制御が可能になりました。具体的には100次元の写像によるモデリング＋50Hzの制御が可能になった例があります。

また、エンコード関数の行先の高次元空間が無限次元の場合、厳密に任意のシステムをエンコード関数とクープマンオペレータで表現できることが解っています。

先行研究は主に二つの方向に進化していて、片方はカオス分野などの専門家がクープマンオペレータのスペクトル解析などをガンガン行って理論的に進めている研究と、KOTをアプリケーション的に利用するためにアルゴリズムなどを作り実際の問題に適用する研究、となっています。

今回紹介する論文、「Deep Koopman Operator With Control for Nonlinear Systems」はその後者の典型的な例になります。

定義

まず問題を数式で表現します。制御状態をx_k、制御入力をu_k、に対して次のような非線形システムがあるとします。

x_{k+1}=f([x_k,u_k])

ここでKOTではエンコード関数gとクープマンオペレータKを用いて、モデルを構築します。
すなわち、z_k=g_x(x_k)のように制御状態を写像します。

また制御入力も同様に写像しますが，ここで問題があります。それは制御入力の写像の仕方によっては線形性が失われるという問題で、この問題に対処するため本論文では三つの方法を提案しています。

  1. DKUC（論文中名称）\phi_k=u_k=g_u(u_k) これは線形性を保つ
  2. DKAC（論文中名称）\phi_k=g_u(x_k)u_k これは線形性を保つ
  3. DKN（論文中名称）\phi_k=g_u(x_k,u_k) これは非線形になる

本論文ではDKUCとDKACは制御と予測の両方、DKNは予測のみに用いられています。

この写像により

z_{k+1}=Kz_k+K'\phi_k

となるような線形システムへ変換できるとみなします。

論文「Deep Koopman Operator With Control for Nonlinear Systems」での実装

問題はg_x,g_u,K,K'をどう計算するかということ、今回の論文ではすべてDNN（ニューラルネット）に学習させます。
（K,K'は一緒にまとめて一つのバイアスなし線形レイヤーとします。）

補足

学習後に予測を行う場合やDKACの場合は各時間でのx_kが知りたいですが、ここで我々が知っているのは（学習後の話なのでg_x,g_u,K,K'が既知とすると）、x_0とg_xなので、z_0が解ります。またK,K'によりz_1以降がわかるので、未来を予測するにはg_xの逆関数が必要になります。

しかし、一般にDNNは非可逆なのでg_xの逆関数は簡単には計算出来ないので何らかの処方箋が必要となります。ここでは二つの方法を上げます。
1つは単純にオートエンコーダ形式のように同時に逆関数のDNNも学習を行う場合であす。
2つ目は本論文で用いられている方法で、z_kのベクトルの要素にx_kをすべて含ませる方法です。こうするとC=[I,O]という単位行列とゼロ行列からなる行列の積を計算するのみでx_k=Cz_kと計算できるようになります。

損失関数

損失関数には「K step foward loss」と「K step encode loss」の二種類を用いられています。
前者は、学習データから例えばx_0,x_1,...,x_Kを用いて、これらをg_xにより写像したz_0,z_1,...,z_Kを得ます。
そしてx_0のみを用いてz_0を計算し。K,K',u_0,u_1,...,u_Kとg_uを用いて、z_{k+1}=Kz_k+K'\phi_kの関係より求めた\hat{z}_0,\hat{z}_1,...,\hat{z}_Kを計算します。
この二つのMSEを誤差とする損失関数が「K step foward loss」です。

後者は簡単で、先ほどのx_k=Cz_kの関係とz_k=g_x(x_k)の関係が正しく一対一の関係にする損失関数で、\hat{z_k}と\hat{\hat{z_k}}=g_x(C\hat{z_k})の二つが持つ誤差を損失とします。
（\hat{\hat{z_k}}=g_x(C\hat{z_k})はデコードしてエンコードするので本来元の\hat{z_k}に一致します。）

以上で概要の説明を終わります。

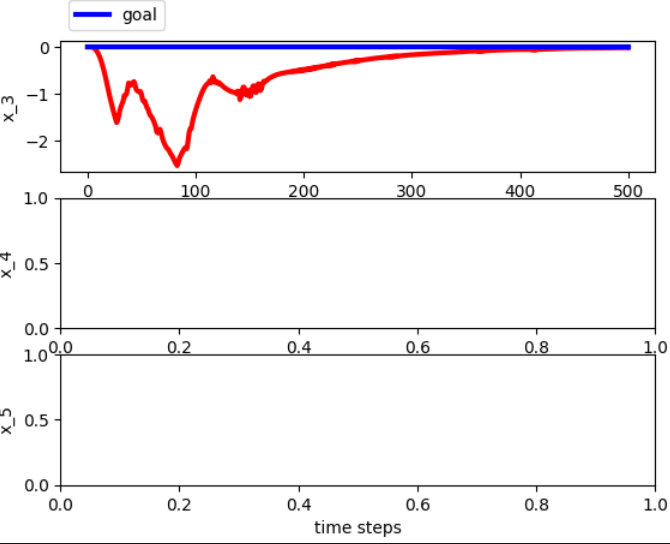
実験結果

今回はソフトロボットのシミュレーターでの制御結果を示します。シミュレーターはsomogymというソフトロボット用シミュレーターを用いました。
また、エンコード関数はDKACを採用し、写像の行先の空間の次元は128次元としました。
制御自体は線形のモデル予測制御で良いため、今回はpython osqpという凸最適化ソルバを用いました、
ワンステップの制御入力の最適化には2.52e-02s程度とリアルタイム制御が可能な範囲といえる結果となりました。
（c++ osqpなどを用いればより高速になります。）


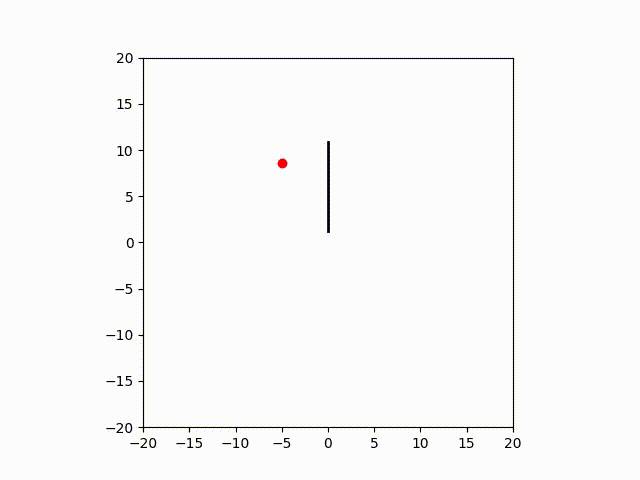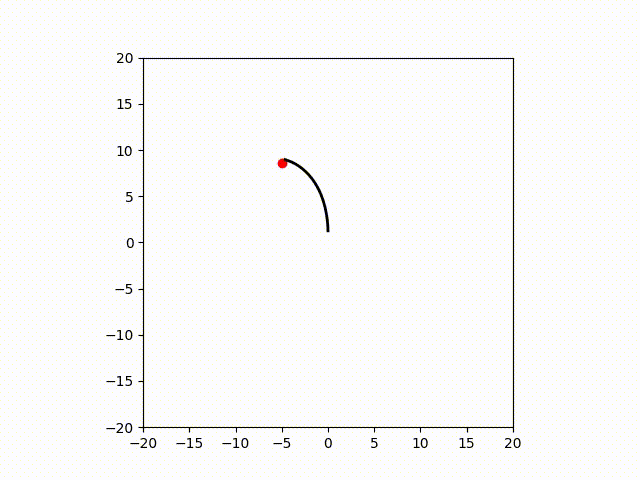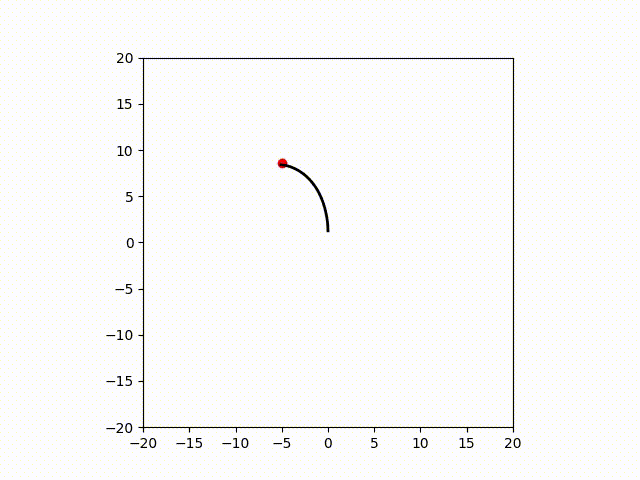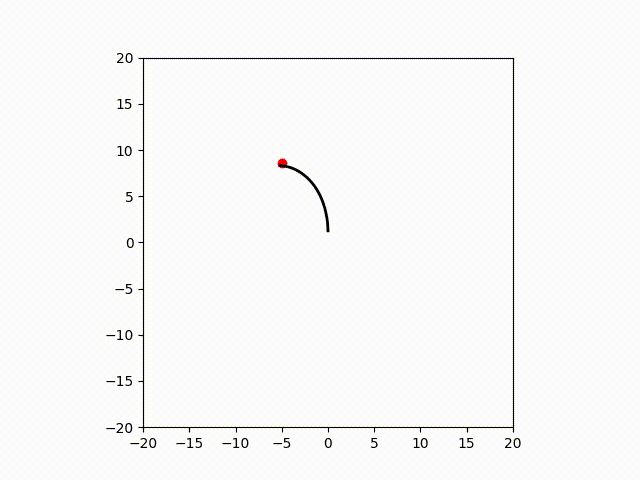
Discussion