冷たいNANDとド・モルガン博士たち
ULX3SもTinyFPGA BXも指くわえて見てるだけ
もうVerilog HDL学べばいいんじゃね。もしくはSystemVerilogか。
でも、すべてがNANDになるのは、ちょっとキャッチーだったかも。
すべてがNANDになる。もしくは?
NOTもANDもNANDになりました。すべてがNANDになります。もしくは?
ということで、OR。
書くまでもない気がしますが、Pythonで念のため確認。
print(False or False) # False
print(True or False) # True
print(False or True) # True
print(True or True) # True
これもNANDになりますか。
ところで、NOT二回つなげても変化なかったですよね。
当然ながらPythonでも変わらない。
print(not not (False or False)) # False
print(not not (True or False)) # True
print(not not (False or True)) # True
print(not not (True or True)) # True
そういえば。
さっきからずーっと気になってたんですが、タイトルに聞いたことがあるようなないような文字列が。
『冷たいNANDとド・モルガン博士たち』
そうそうド・モルガン ド・モルガン。Augustus de Morgan。
あれだ、あれあれ、ド・モルガンの法則。
ド・モルガンの法則、といきなり言われても困ります。
身近なものでおさらいしましょう。ハロウィンで。
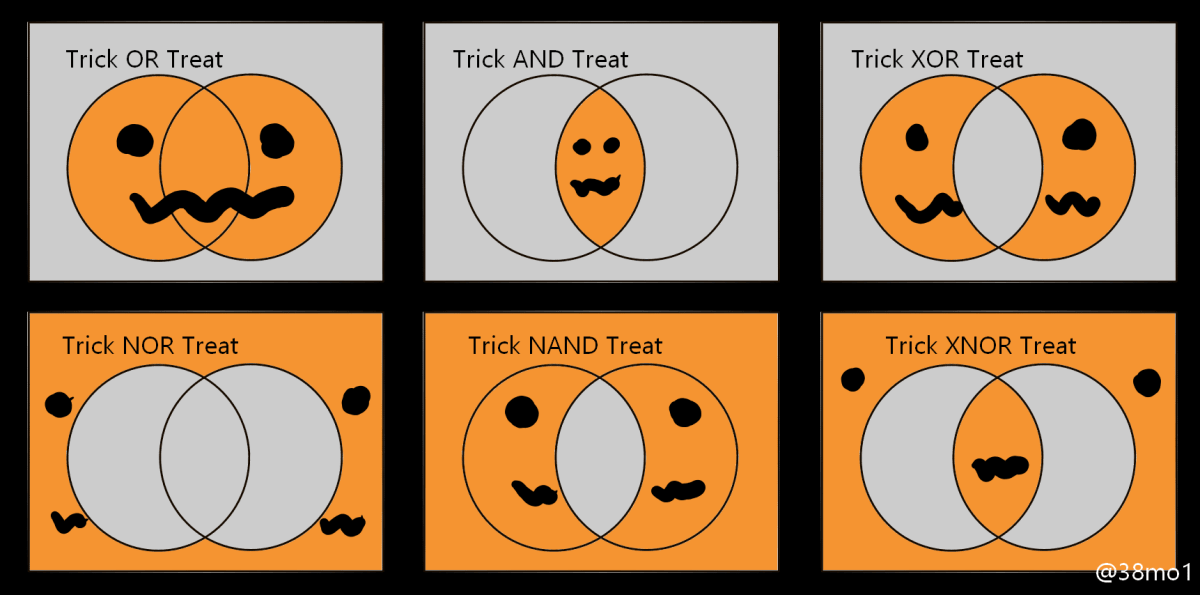
わかりやすい。
ベン図ですね。ベンさんえらい。
この図のなかで、注目したいのは左下。Trick NOR Treat。
NORというのは(NANDがNOT ANDであるように)、NOT OR。
NOT ORといえば、ここ!
このNOT ORをド・モルガンの法則で入れ替えます。
PythonでNOT ORを書くと、このとおり
not (Trick or Treat)
先ほどのベン図からNOT ORを抜粋。
この色のついた部分「NOT OR」を、ド・モルガンの法則で別の何かに入れ替えるわけです。
先に答えを書いてしまうと、Pythonでは
(not Trick) and (not Treat)
ベン図ではこう。
ソフトウェアでもおなじみですよね。
!(Trick || Treat) == (!Trick && !Treat)
ベン図を分解して確認しなおします。(not Trick)と
(not Treat)、
この2つのAND。
ね。
# (not (Trick or Treat)) == ((not Trick) and (not Treat))
Trick = False
Treat = False
assert ((not (Trick or Treat)) == ((not Trick) and (not Treat))) # True
Trick = True
Treat = False
assert ((not (Trick or Treat)) == ((not Trick) and (not Treat))) # True
Trick = False
Treat = True
assert ((not (Trick or Treat)) == ((not Trick) and (not Treat))) # True
Trick = True
Treat = True
assert ((not (Trick or Treat)) == ((not Trick) and (not Treat))) # True
あってる! 記号で描き直すとこうなります。
さっそく、このNOT ORを入れ替えて見ましょう。
NOT 2つにANDですね。
あ、NOT ANDだ!
当然NOT ANDはNANDに入れ替えられます。
NOTも、すでに証明されたとおり、NANDに入れ替えられますよね。
完成!
Pythonでの追試も👍
print(False or False) # False
print(True or False) # True
print(False or True) # True
print(True or True) # True
def nand(a, b):
return not (a and b)
print(nand(not False, not False)) # False
print(nand(not True, not False)) # True
print(nand(not False, not True)) # True
print(nand(not True, not True)) # True
すべてがNANDになる
NOTもANDもORもNANDになりました。すべてがNANDになります。
Discussion
次作は「笑わないNAND」でしょうか?