XORしない数学者 (ゲームに学ぶFPGA)
MHRD 楽しんでらっしゃいますでしょうか?
3つのハードウェアデザインゲーム(The Nand Game、MHRD、Digital Logic Design (The Game))のうち、わたしの超推しはMHRDです。コードを画面内に納めないといけないとか、コピペもままならない(できるけども)とか、このもどかしさとわけわからなさを味わっていただきたい。
『すべてがNANDになる』という言説どおり、そしてそれらの3つのゲームどおり、NOTもANDもORもNANDになりました。すべてがNANDになります。
XOR
NOT、AND、ORときたら、次はXOR。
Pythonだと ^ ですよね。
print(False ^ False) # False
print(True ^ False) # True
print(False ^ True) # True
print(True ^ True) # False
XORもNANDになりますか。
Trick XOR Treat
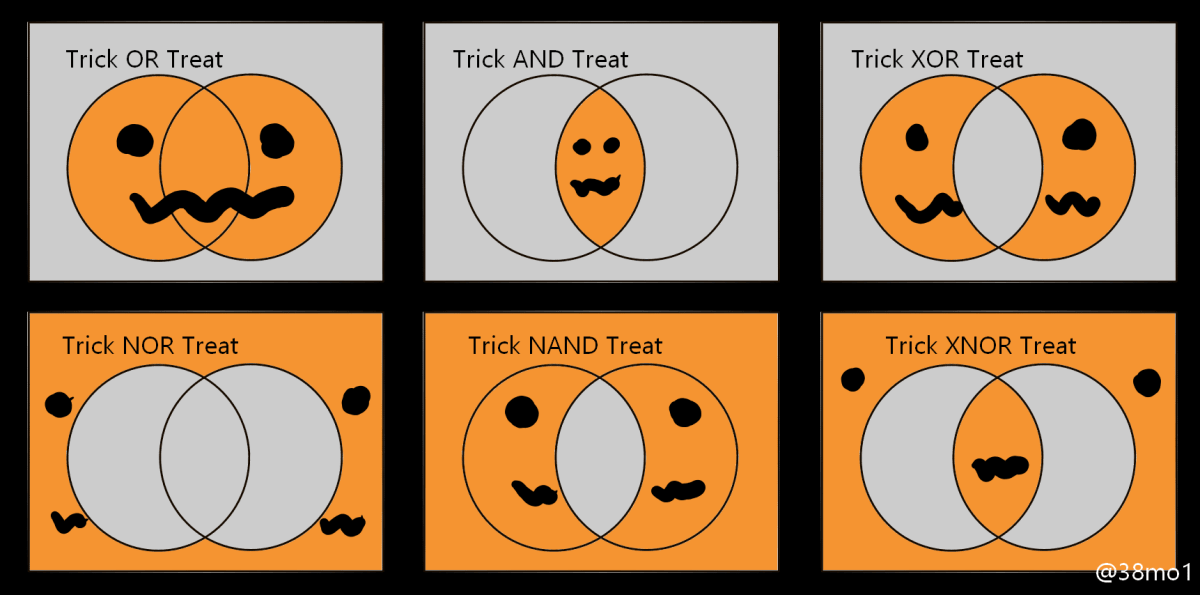
今回注目したいのは右上。Trick XOR Treat。
じっと見ると見えてくる、XORの作り方。ANDで重ねあわせれば、同じ色のところだけ残ると。
Pythonで書き下せば、Trick ^ Treatはこのとおり。
(Trick or Treat) and (not (Trick and Treat))
テストしときましょう。
Trick = False
Treat = False
assert (Trick ^ Treat) == ((Trick or Treat) and (not (Trick and Treat)))
Trick = True
Treat = False
assert (Trick ^ Treat) == ((Trick or Treat) and (not (Trick and Treat)))
Trick = False
Treat = True
assert (Trick ^ Treat) == ((Trick or Treat) and (not (Trick and Treat)))
Trick = True
Treat = True
assert (Trick ^ Treat) == ((Trick or Treat) and (not (Trick and Treat)))
記号で書き表すと、こう。
完成!
って、なんかNANDの数、多くないですか。XORに6個もNAND必要?
ブール代数による解法
こっから先はANDとかORとかNOTとかNANDとかよりも、数学的にわかりやすいブール代数を使わざるを得ない。
ブール代数とか、かしこまっていっても、結局orを+にして、ANDを・にして、NOTは頭に−をかぶせるだけ(NANDはNOT ANDだから、ANDを・にして、頭に−をかぶせるだけ)。
なんでブール代数を使うかというと、分配法則が使いたいから。
ブール代数!? 分配法則!? なんかややこしそう。
って実は、中学数学での分配法則と同じ。これ。
(A + B) × C = (A × C) + (B × C)
ブール代数式でのXORのうち、A + Bを分配すると、このとおり。
記号で描いて見ましょう。これが分配前のXOR。
そして分配法則により(A or B)が分配されて、(A and (A nand B)) or (B and (A nand B))に。
ORの階層を上げて、OR以下をまるっとコピーした感じですね。
しかし、何かだまされた感。本当に同じかどうか、Pythonでテストしときましょう。
def nand(a, b):
return not (a and b)
def xor(a, b):
return a ^ b
def xor_version1(a, b):
return (a or b) and nand(a, b)
def xor_version2(a, b):
return (a and nand(a, b)) or (b and nand(a, b))
A = False
B = False
assert xor(A, B) == xor_version1(A, B) == xor_version2(A, B)
A = True
B = False
assert xor(A, B) == xor_version1(A, B) == xor_version2(A, B)
A = False
B = True
assert xor(A, B) == xor_version1(A, B) == xor_version2(A, B)
A = True
B = True
assert xor(A, B) == xor_version1(A, B) == xor_version2(A, B)
あって... いる、だと? あってます。
で、分配法則はわかったけど、なんで分配したのか説明してなくない? それは、その方がNANDの数が減るから。あとで記号で表すと見えてくる。
この式で、目ざわりなのは +。つまり OR。ORはNANDを3つも使うので消し去りたい。
何度もやっているように、NOTを2回つけても、式としては変化なし。
NOTにORとくれば、おなじみド・モルガンの法則。
Pythonでド・モルガンの法則を書けば、以下のとおり。
not (A or B) == ((not A) and (not B))
Javascriptなら、こう。
!(A || B) == (!A && !B)
ブール代数のXOR式にあてはめれば、このとおり。
完成!
... 完成?
完成!
なぜならば、この最終形態はNANDのみでできてます。まずこの二ヶ所。
次に、一つ上のこの二ヶ所。
最後に、式全体。
つまり、5個のNANDですね。
... ではなく、このA nand Bを使いまわせば、4個ですむんです。
記号で描けば一目瞭然。
念のため、一つ一つ確認してみます。まず、一番内側のNAND。このA nand Bを使いまわせば、の部分ですね。
次に、一つ上のこの二ヶ所。
最後に、式全体。
以上で、XOR完成!
Pythonでテストしときます。
def nand(a, b):
return not (a and b)
def xor(a, b):
nand_a_b = nand(a, b)
return nand(nand(A, nand_a_b), nand(B, nand_a_b))
A = False
B = False
assert (A ^ B) == xor(A, B)
A = True
B = False
assert (A ^ B) == xor(A, B)
A = False
B = True
assert (A ^ B) == xor(A, B)
A = True
B = True
assert (A ^ B) == xor(A, B)
問題なし!
論理回路からの解法
分配法則をあてた後の論理回路から見直してみます。
同じ論理回路である(A nand B)は、当然一つにまとめられます。
見やすさを優先してNANDではなくNOTを使ってます。
うーん... 冗長だ。
NOT NOTは、二重否定的に、消せないわけはないですよね。
消した! あ、NANDが4個だけ! さっきと同じ!
ということで、XOR完成!
Verilog HDLからの図式
JavascriptでのXORは
OUT = B ^ A
Verilog HDLだと
module top (
input A,
input B,
output OUT
);
assign OUT = B ^ A;
endmodule
こんなんですね。
呪文を唱えて、このVerilog HDLコードを図式してみると
yosys -q -p "
read_verilog xor.v
synth -top top
abc -g NAND
show -format svg -prefix xor
write_json -compat-int xor.json
"
Yosys abcによる変換だと、NANDは5個でした。
netlistsvg and.json
すべてがNANDになる
難関XORもNANDになりました。すべてがNANDになります。
Discussion