時系列データ考察のための可視化手法実装例

目次

• 本記事の目的
• 季節性の分解
• 類似時系列の可視化
• 変化点検出
• 相互相関の可視化
• 本記事のまとめ
• 参考文献

本記事の目的

機械学習やAIを用いた予測において重要な項目の1つに、説明可能性があります。これは、学習結果に対してなぜその結果になったのかを説明可能かというものです(参考文献1)。例えば予測結果の誤差が小さかったとしても、予測結果を意思決定に用いる場合、過去データと予測結果の関係性を考察できなければ、正確な意思決定ができない可能性があります。
　前記事では、Transformerの改善モデルであるiTransformerを用いて複数の時系列データの需要予測を行いました。その課題点として、予測結果を考察可能な可視化方法の実装がありました。また、予測時系列データを選択する上で、時系列クラスタリングによる方法を考えましたが、sckit leranのチートシートを見ても分かるように、クラスタリングにはデータ数が必要になります(参考記事3)。したがって、データ数が少ない場合は時系列データの類似性の可視化をして判断をするのがよいと考えました。類似性を可視化することにより、前述の予測結果の考察にも使用可能と考えました。
　そこで本記事では、時系列データ予測の結果を考察するための方法として、時系列データの可視化方法を実装していこうと考えています。具体的には、季節性の分解、類似時系列の可視化、変化点検出、相互相関の可視化の4つの実装をしていきます。そして実装結果に対して前記事の内容を説明できるかを検証し、有用性を見出せたらと考えています。

季節性の分解

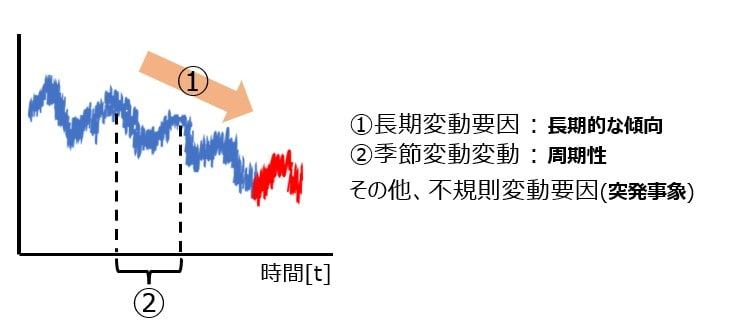
時系列データは、長期的な需要の傾向を示すトレンド成分、夏に需要が増え、秋から冬にかけて需要が下がっていく、というような季節変動要因である周期成分、突発的需要など他の変動要因である誤差成分に分解できます(参考文献4、参考文献5)。

pythonでは元の時系列データに対して、この3成分を分解して抽出することができます(参考文献6、参考文献7)。そこで、seasonal_decomposeを使った分解をやっていきます。なお、データは前記事同様、政府統計ポータブルサイトであるe-Statと統計ダッシュボードのデータである、機械受注統計調査、および、日経平均株価のデータを使用し、加工をしていきます。
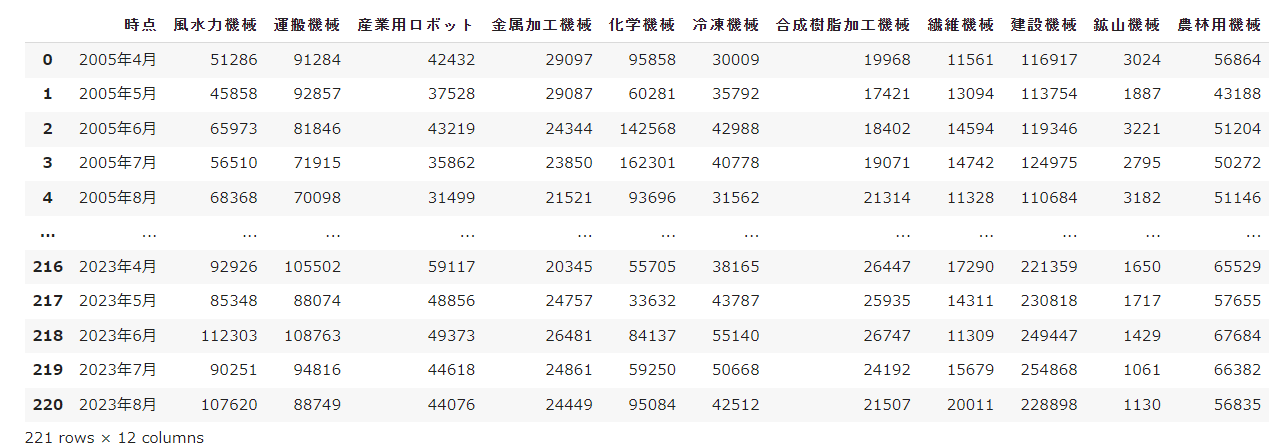
　機械受注調査の内容は以下の通りです。

　日経平均株価は以下の通りです。

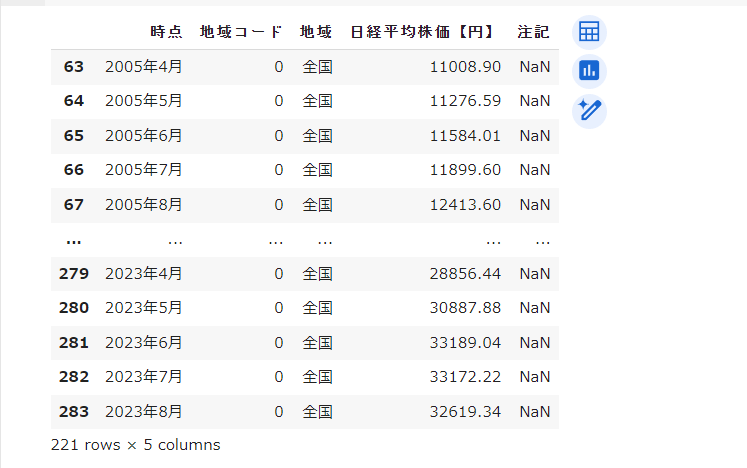
　前記事では、産業用ロボット、風水力機械、運搬機械、金属加工機械、冷凍機械、合成樹脂加工機械の6つと、日経平均株価の合計7つのデータセットを用いています。また、log10で対数を取り階差を取っています。そこで、行のインデックスを時刻、列に各項目を取り、データに階差を格納したdf_tempを定義します。なお、後述の類似度測定の都合上、正規化も実施しています。

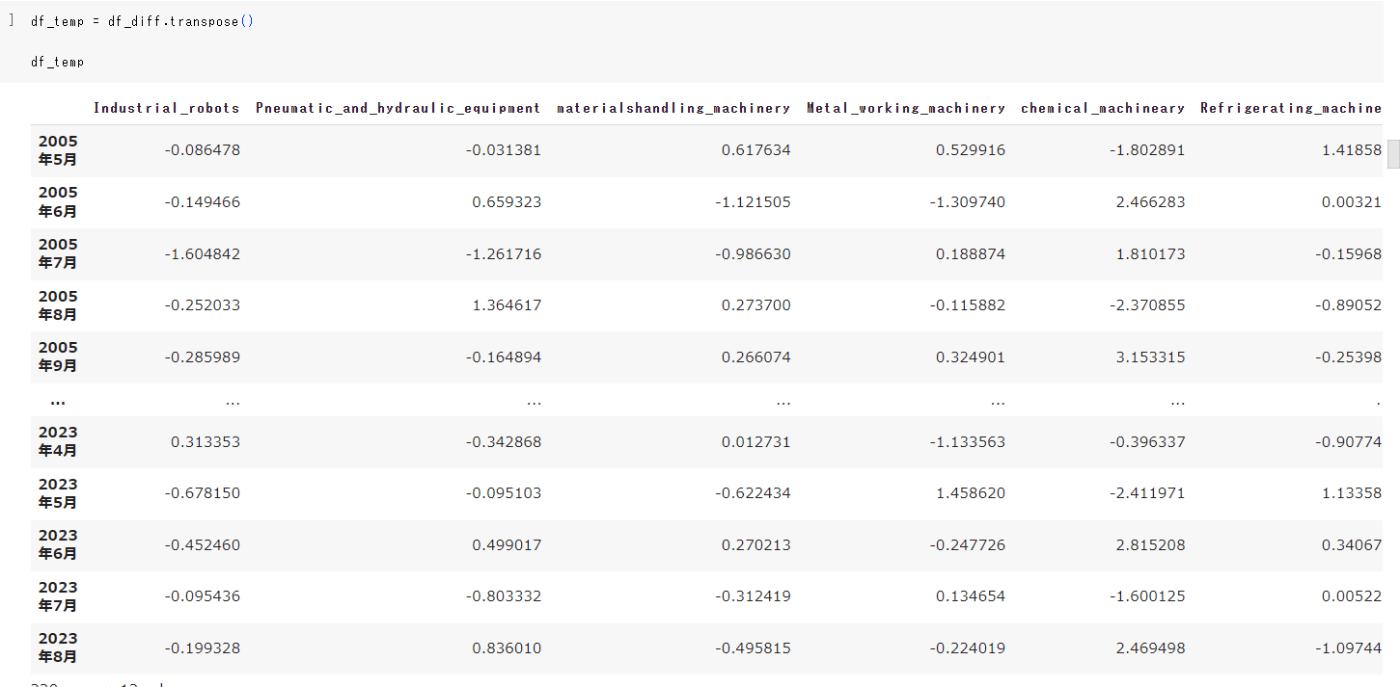
　では分解を行っていきます。なお周期は、前記事でバッチサイズとして定義した、36で実装しています。

seasonal_decompose.py

import statsmodels.api as sm

period = 36
# 時系列データを格納するためのリストを作成
timeseries_data = [df_temp[col].dropna().values for col in df_temp.columns]

# 季節性分解を実行
result = [sm.tsa.seasonal_decompose(data, period=period) for data in timeseries_data]

# トレンド成分、季節成分、誤差成分を抽出
trend_components = [res.trend for res in result]
seasonal_components = [res.seasonal for res in result]
residuals = [res.resid for res in result]

# 各成分のデータフレームを作成
df_seasonal = pd.DataFrame(data=seasonal_components,index=index_lists,columns=months)
df_seasonal = df_seasonal.dropna(axis=1)
df_trend = pd.DataFrame(data=trend_components,index=index_lists,columns=months)
df_trend = df_trend.dropna(axis=1)
df_residuals = pd.DataFrame(data=residuals,index=index_lists,columns=months)
df_residuals = df_residuals.dropna(axis=1)

分解した成分、および、元データを描画する関数は以下のように実装しました。

DrawGraph.py

#各項目の図をk描画する関数
def DrawGraph(df,index,title,imgfloder) :
  for i in range(0,len(df)) :
    plot_index =  df.iloc[i]
    plot_index.plot(figsize=(10, 6))
    plt.title(index[i] + title)
    plt.savefig(imgfloder + index[i] + title)
    plt.show()

例えば、産業ロボット、および、日経平均の階差の元データと各成分の描画結果は以下の通りです。

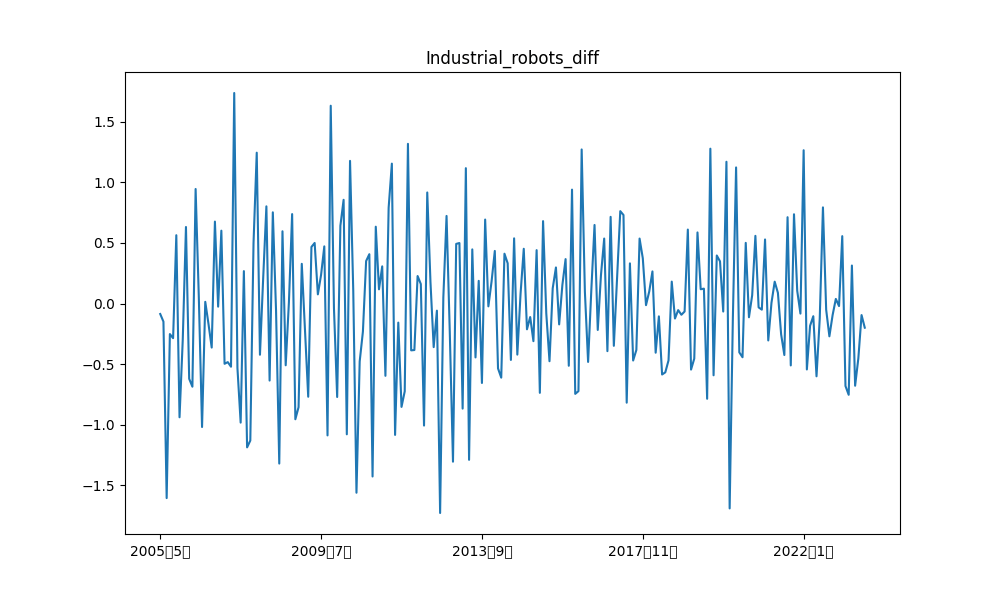
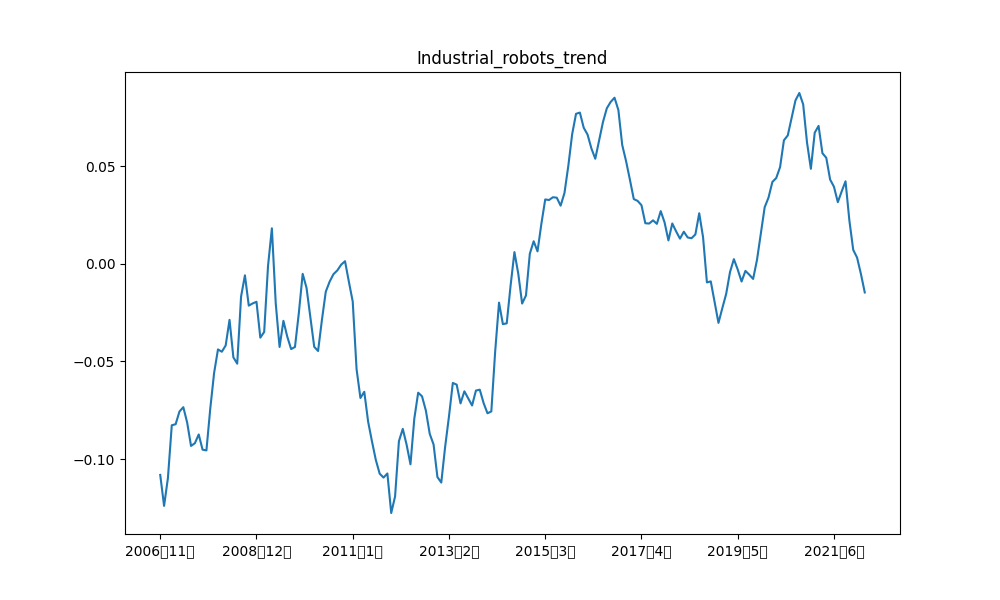
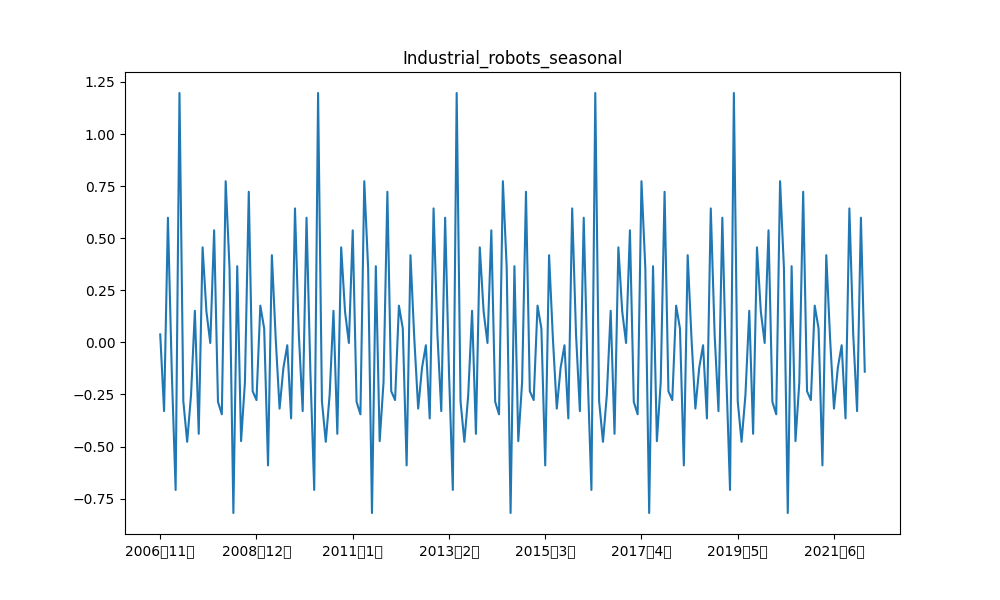
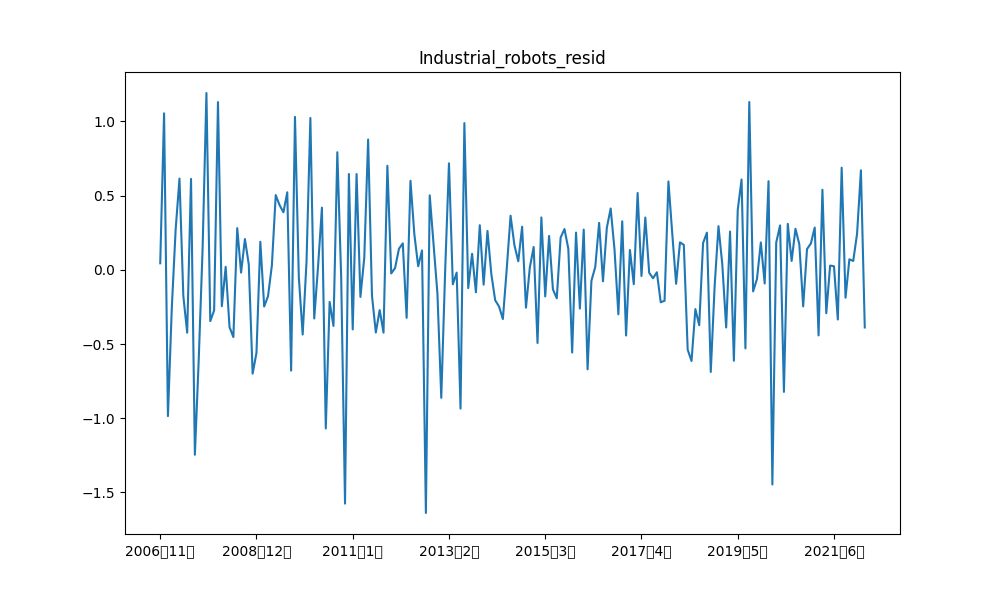
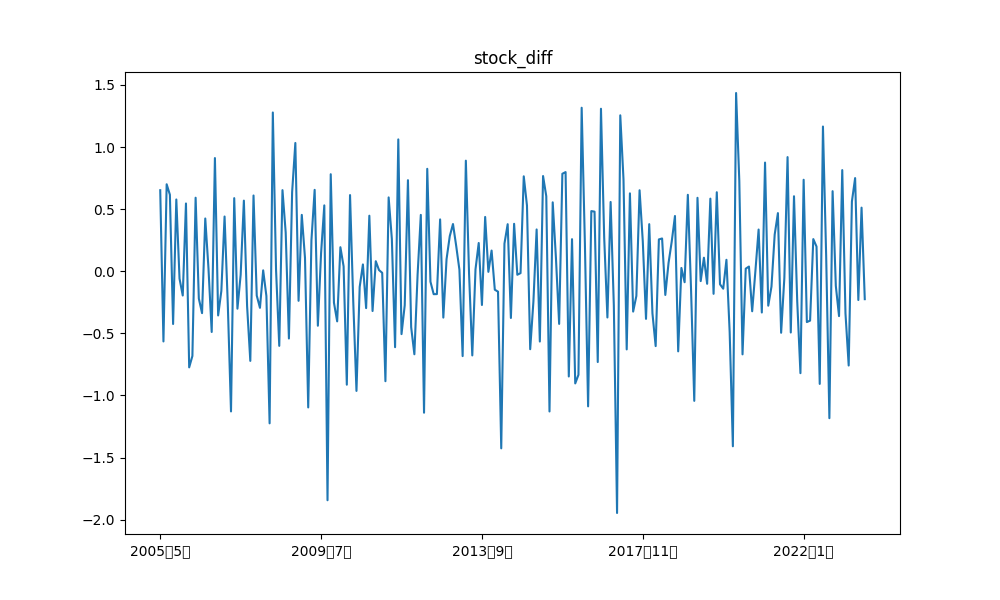
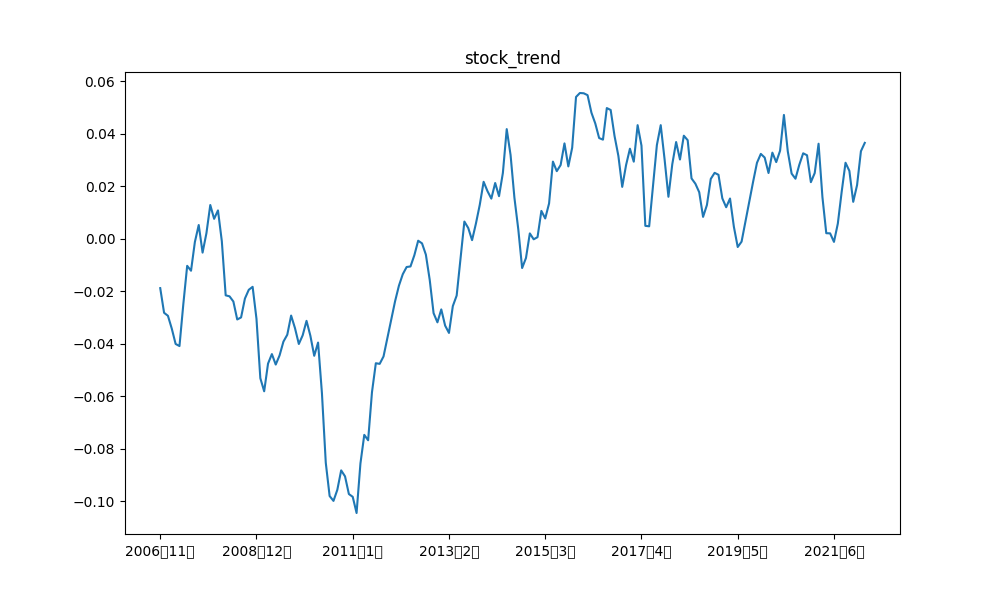
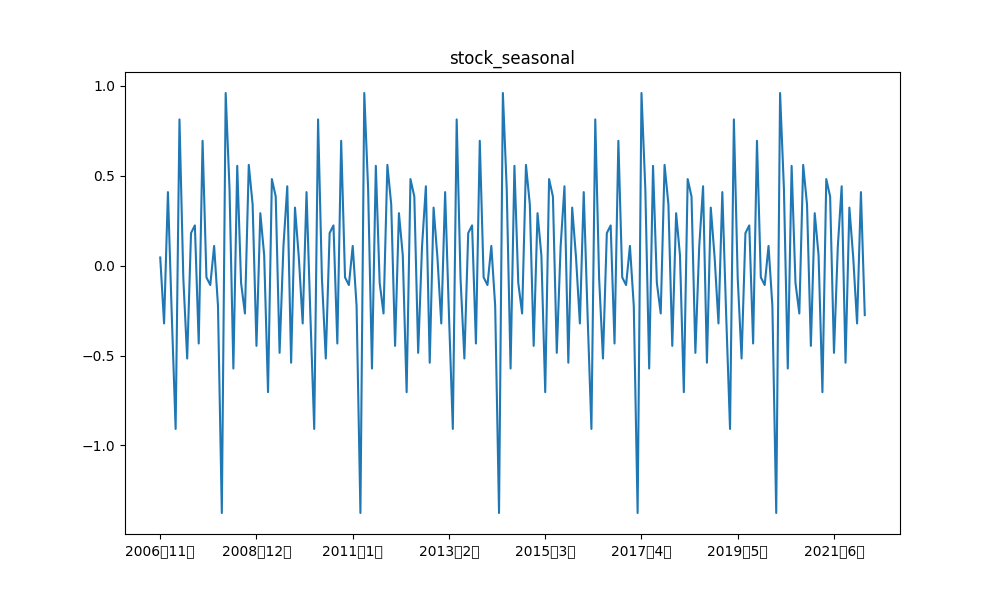
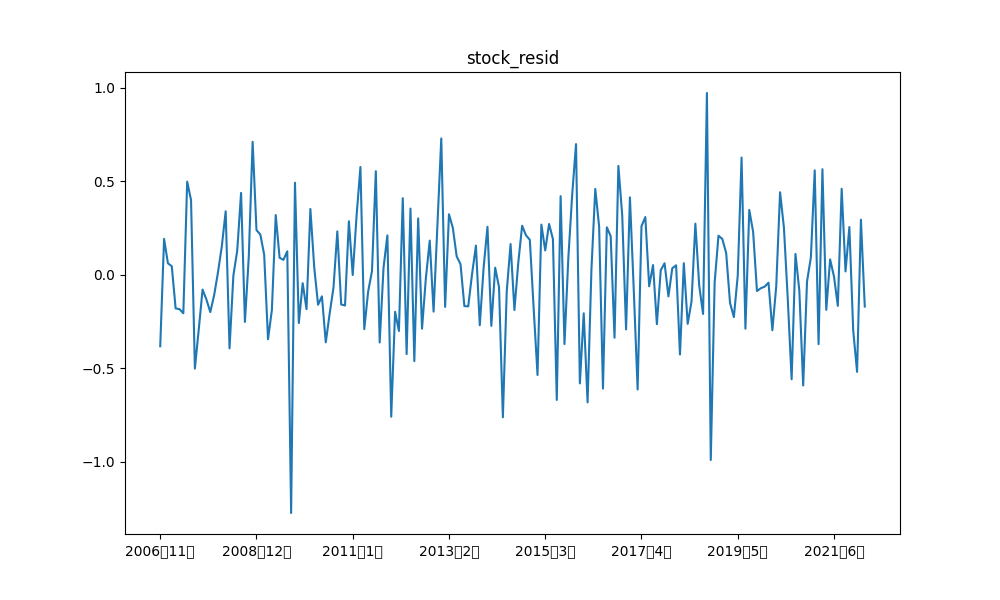
類似時系列の可視化

前節では季節性の分解を実施しました。次に類似時系列を可視化することにより、多変数での需要予測をする際の時系列データの選択の1つの手法になると考えました。本記事では、DTW(Dynamic Time Warping)を用いて類似度を算出しました。また可視化の方法として、ヒートマップを選択しました。ヒートマップのカラーマップを調べてみましたが、色の濃さが変わるもの、色自体が徐々に変わるものが多かったです(参考文献8)。類似度を目で見て分かるように、今回は色の濃さが変わるものをカラーマップとして選択しました。類似性を色で判断する場合、色が濃くなればなるほど類似性が高いというのが感覚的には理解しやすいと考えています。しかしながら、DTWは類似性が低いほど値が大きくなる傾向があるので、1 – DTWとすることで、類似度が大きいほど色が濃くなるように可視化しました。

Draw_DTW_sns.py

import seaborn as sns
from tslearn.metrics import dtw

#ヒートマップによる類似性可視化関数
def Draw_DTW_sns(df_dtw,index,title,color,imgfloder) :
  #sns_dtw : 類似性格納行列
  sns_dtw = []

  for i in range(0,len(df_dtw)) :
    #row_dtw : 各行の類似性
    row_dtw = []
    for j in range(0,len(df_dtw)) :
      #色が濃いほど類似性が高いというルールにするために
      #1からDTWを引く
      DTW = 1 - dtw(df_dtw.iloc[i],df_dtw.iloc[j])
      row_dtw.append(DTW)
    sns_dtw.append(row_dtw)
  
  #ヒートマップの可視化
  plt.figure(figsize=(8, 6))
  column_names = row_names = index
  sns.heatmap(sns_dtw, cmap=color, linewidths=.5,annot=False,xticklabels=index,yticklabels=index)
  plt.title(title)
  plt.savefig(imgfloder + title)
  plt.show()

結果は以下の通りです。まず各成分の類似性を見ていきます。



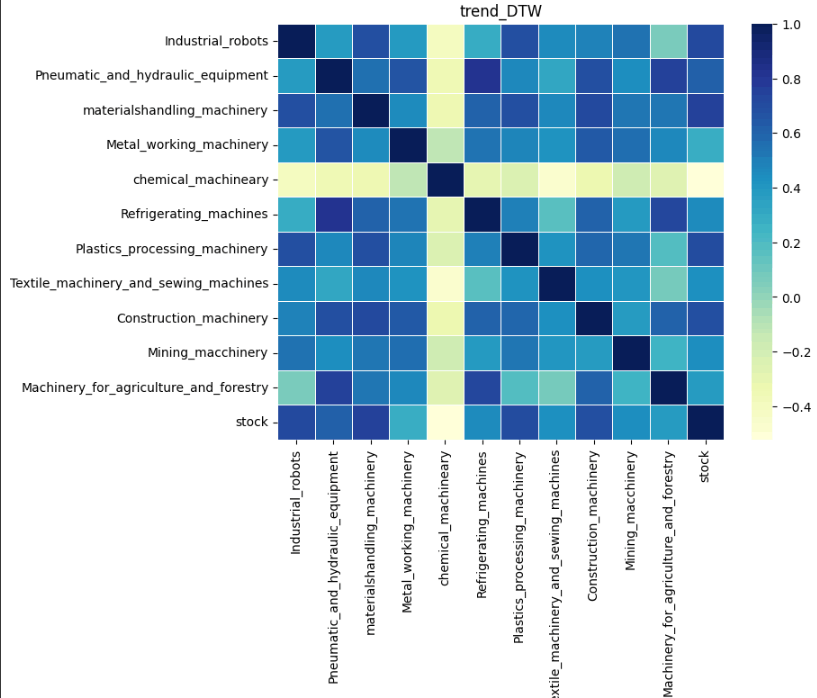
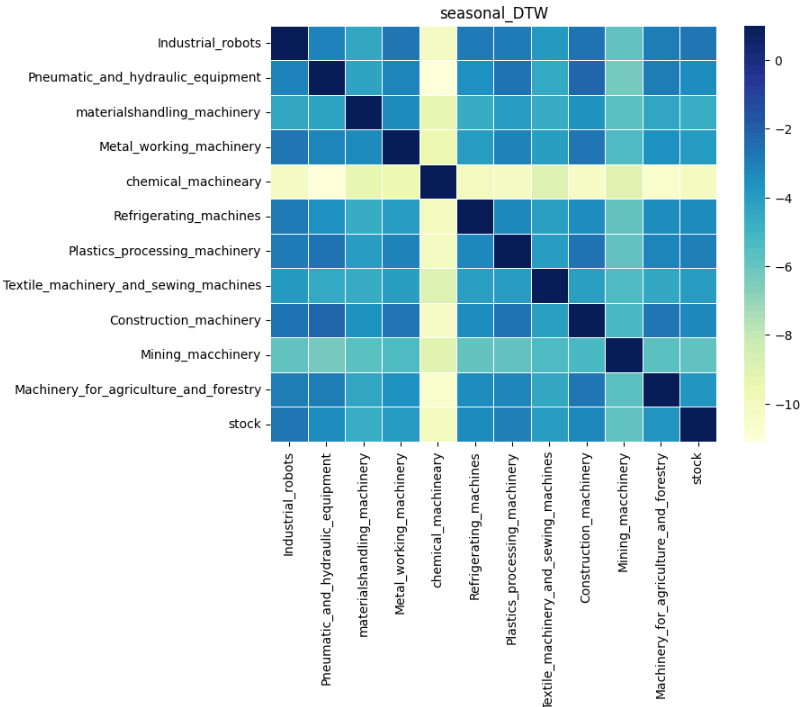
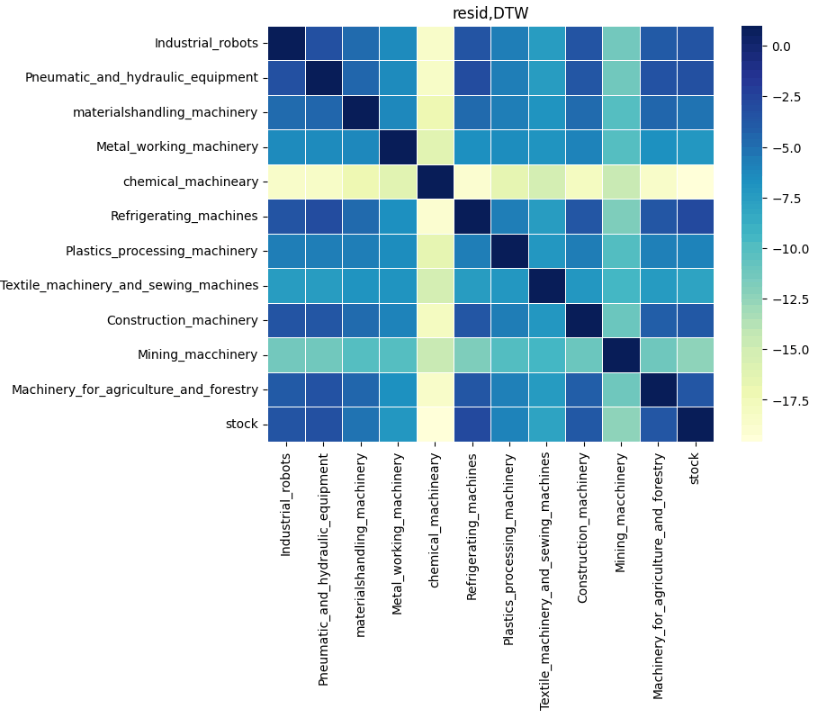
　日経平均との類似性を比較すると、どの成分においても化学機械、および、鉱山機械は類似性が低いことが分かります。実際、log10で対数変換した元の時系列データを比較してみると、日経平均と化学機械、および、鉱山機械は推移が異なっていることが分かります。



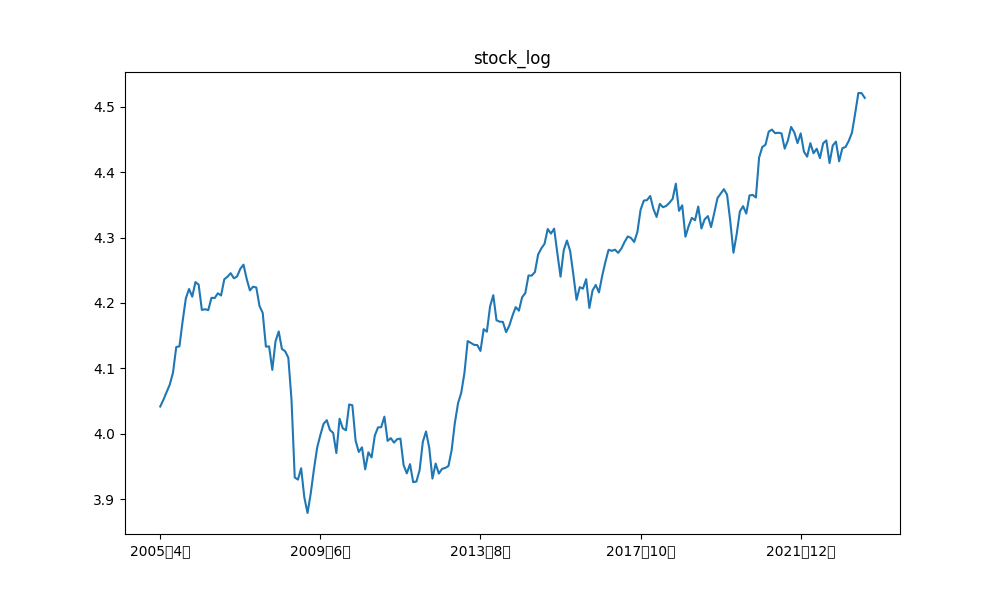
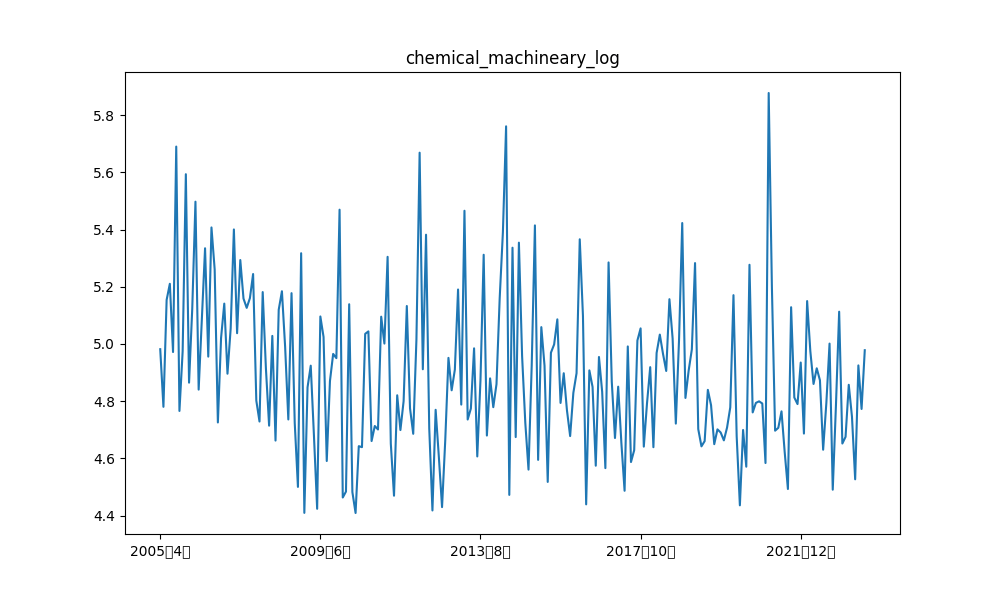
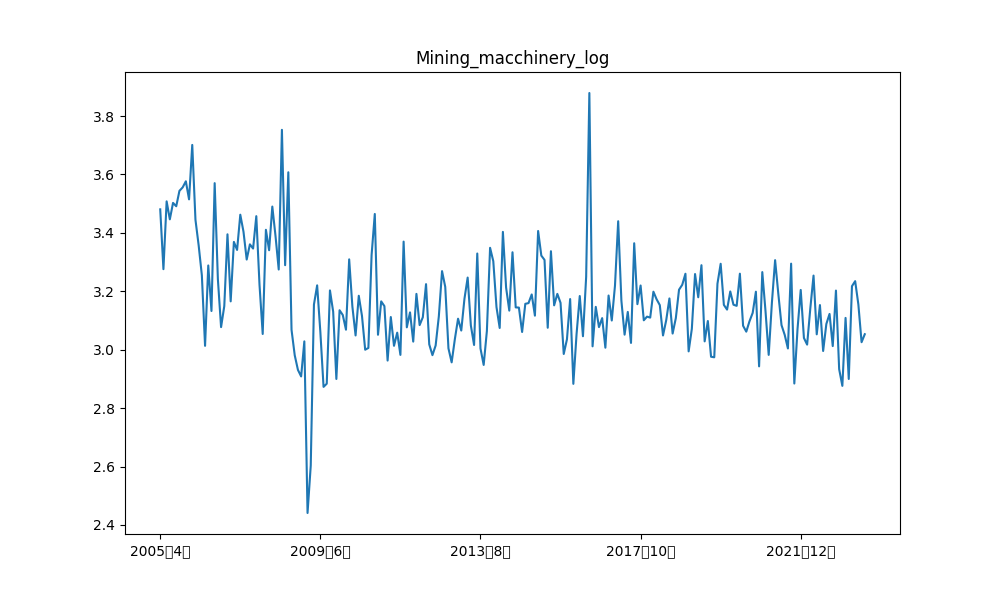
　また、建設機械は各成分との比較では色が濃く類似性が高いように見えますが、対数変換した元データの類似性を見てみると、日経平均株価との類似性は水色(類似性低め)となっており、類似性が高そうなデータ間の取捨選択が可能であると考えています。

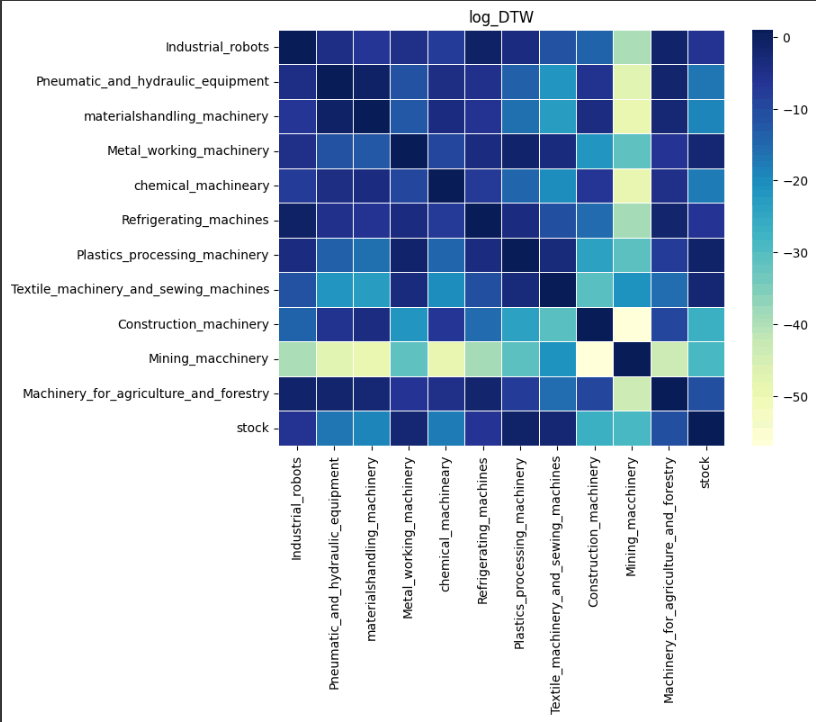
　このように前節の可視化と組み合わせることで、データごとの類似性の大小に対して、視覚的な判断が可能となり、多変数の需要予測における学習データの選定にある程度の有用性があることが分かります。

変化点検出

変化点検出は、時系列データが変化する箇所を検出する手法であり、時系列データの変化の特徴の把握や、変化する前兆の検出が可能になります(参考論文1、参考論文2)。前記事のように、バッチでデータをまとめた上で、多変数で学習を行い、相関を求めつつ予測を行う場合、バッチ内での相関が算出しやすいバッチサイズにすることがよいと考えています。したがって、激しい変化が少ないバッチサイズ(外れ値を少ないバッチサイズ)を考える1つの方法として、変化点検出が有用ではないかと考えました。Pythonではrupturesライブラリで変化点検出が容易にできます(公式サイト)。今回は前記事でバッチサイズとして定義した36と変化点の関係性を可視化していきます。バッチサイズと変化点のF1スコアを最大化するアルゴリズムを実装しました。コードについては、このサイトを流用したので、ここでは割愛させて頂きます。対数変換をした時系列データに対して、バッチサイズと変化点を可視化します。結果は以下の通りです。色付けされたものがバッチサイズによるもの、変化点は太い点線になります。

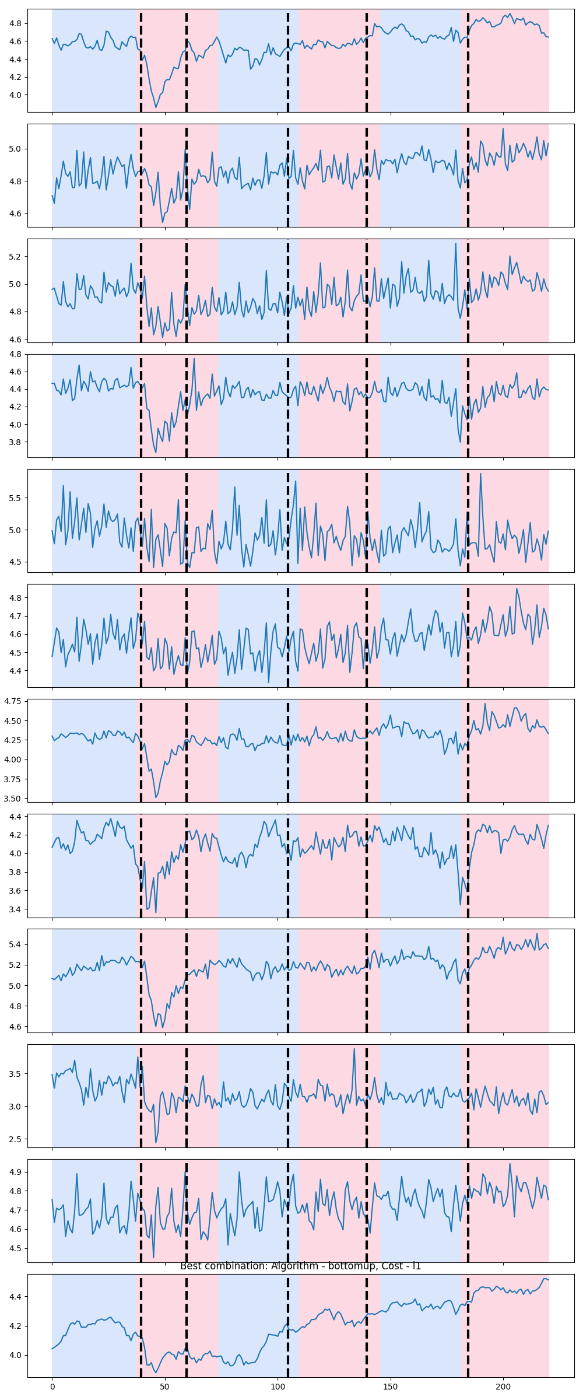
　変化点は、(40,60,105,140,185)であり、バッチサイズは36,72(36×2)・・,180(36×5)なので、2つ目の変化点以外は良い精度で変化点を分けられたバッチサイズになっていることが分かります。前記事では可視化をして判断をしたわけではなかったですが、結果的に変化の激しい箇所をバッチ内にあまり含めずに学習ができたことが、単月ではありますが。予測精度の高い結果を出力できた1つの要因だと考えています。

相互相関の可視化

相互相関は2種類の時系列データ間の相関を測ることができる指標です(参考文献9)。今回はバッチ内での時系列データ同士の相関関係を見ていきます。相関は、xが増加するときyも増加するというような正の相関や、xが増えるとyが減少するというような負の相関があり、値の正負で時系列データ同士の関係性を考察できます(参考文献10)。ヒートマップでの可視化を考えた際、正と負で色が変わった方が視覚的に判断しやすいと考え、カラーマップは色自体が徐々に変わるものを適用しました。また、1から時系列データ長の連番のリスト、Timeを作成し、時間経過に対する傾向を考察可能にしました。実装は以下の通りです。

DrawCorr_sns.py

def DrawCorr_sns(df,batchnum,index,color,title,imgfolder) :
  #変数設定
  rows,columns = df.shape
  batch =  columns // batchnum

  #時間経過を考察するための連番Timeのインデクスに格納
  corr_index = index.copy()
  corr_index.append("Time")
  column_names = row_names = corr_index
  #Timeをデータフレームに追加
  df_copy = df.copy()
  new_index_row = pd.DataFrame([range(1, columns + 1)], columns=df_copy.columns, index=["Time"])
  df_copy = pd.concat([df_copy,new_index_row])

  for i in range(batchnum) :
    #df_batvh : 各バッチの時系列データフレーム
    df_batch = df_copy.iloc[:,batch * i : batch * (i + 1)]
    corr_matrix = []
    for j in range(0,len(df_batch)) :
      corr = []
      for k in range(0,len(df_batch)) :
        #バッチ内での各時系列データの相互相関の算出
        corr.append(df_batch.iloc[j].corr(df_batch.iloc[k]))

      corr_matrix.append(corr)
    
    #ヒートマップの可視化
    plt.figure(figsize=(8, 6))
    sns.heatmap(corr_matrix, cmap=color, linewidths=.5,annot=False,xticklabels=corr_index,yticklabels=corr_index)
    plt.title("batch" + str(i+1) + title)
    plt.savefig(imgfolder + "batch" + str(i + 1) + title)
    plt.show()

結果は以下の通りです。なお、正の相関が強くなるほど赤に、負の相関が強くなるほど青になります。






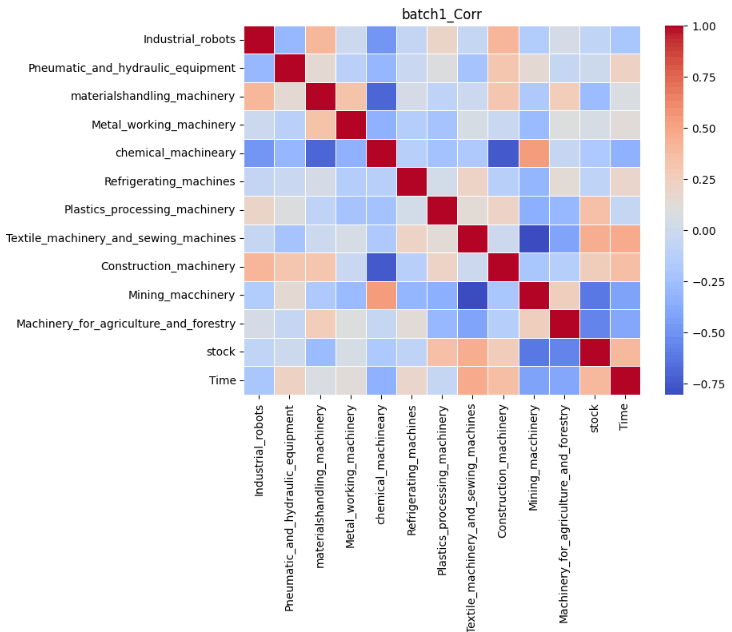
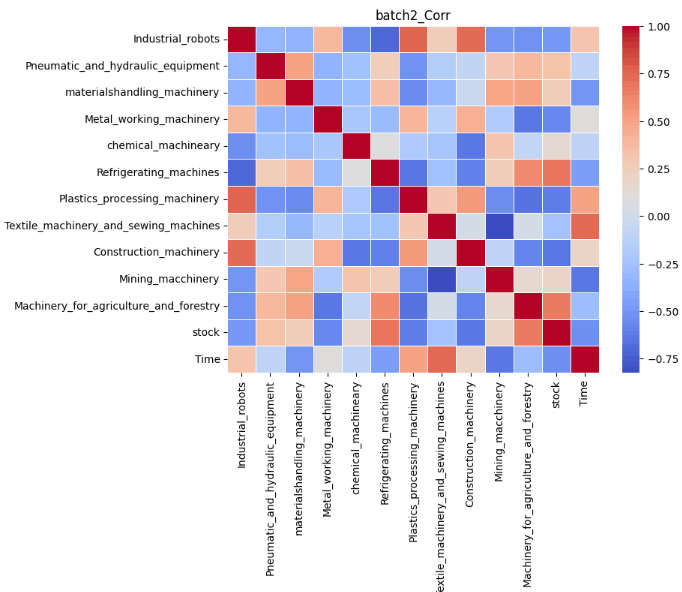
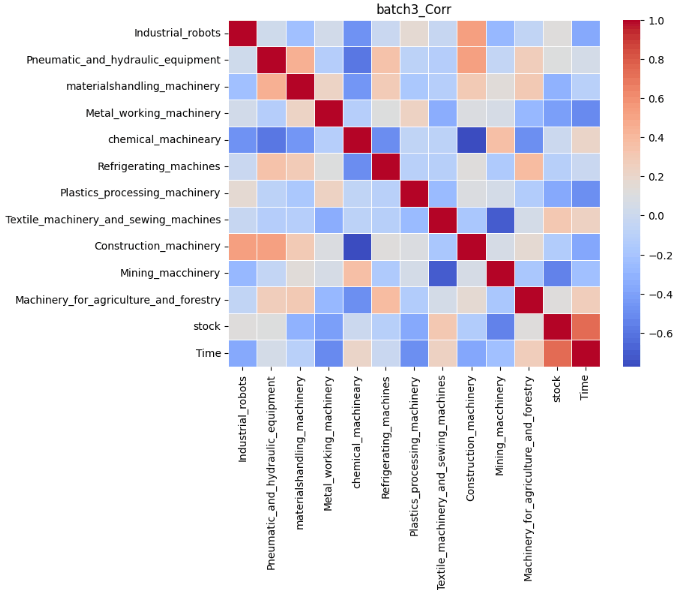
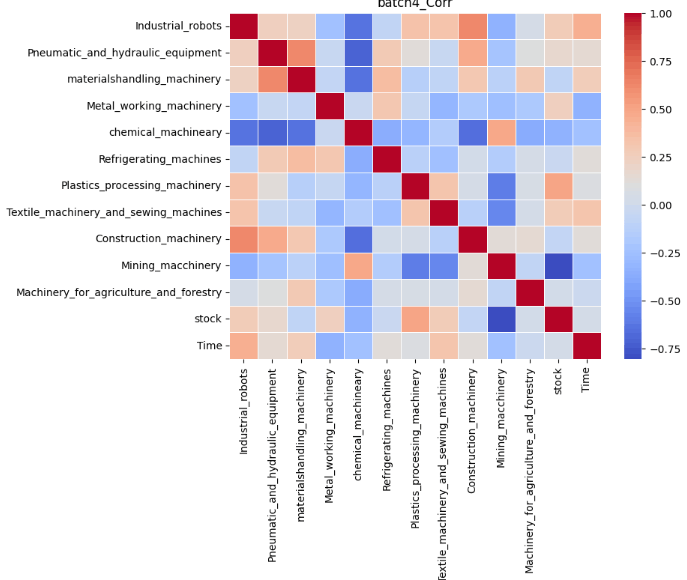
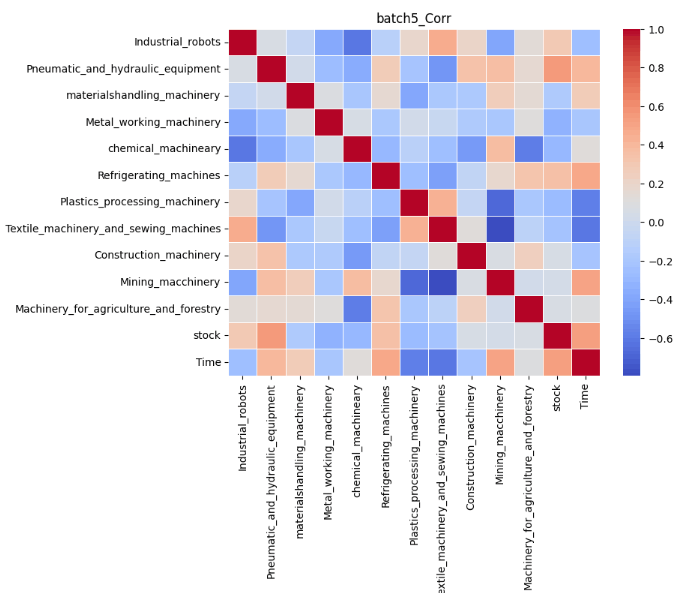
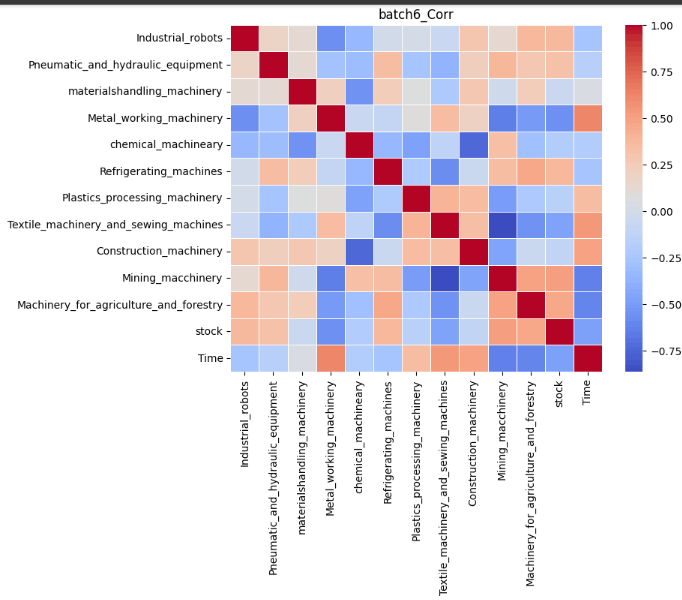
今回は実際の予測をした6つの目のバッチを重点的に考察していきます。前記事の結果は以下の通りでした。


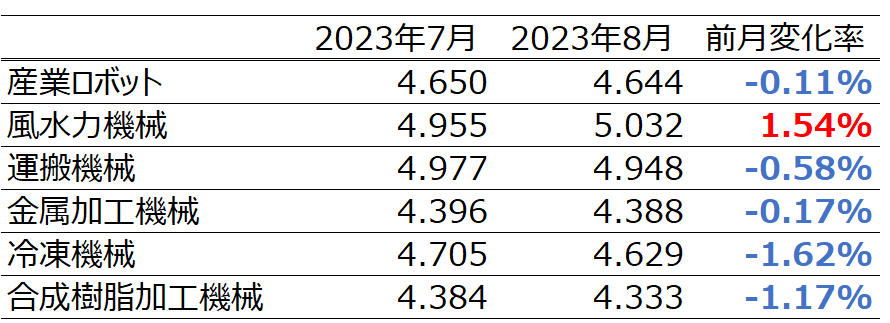
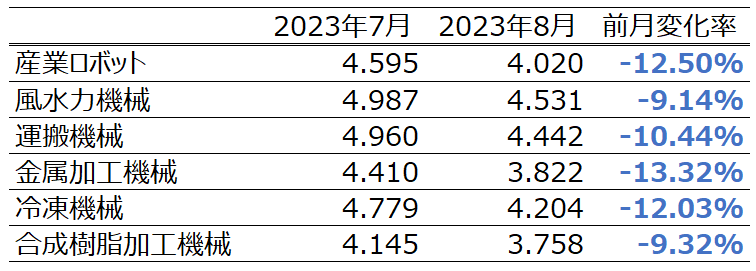
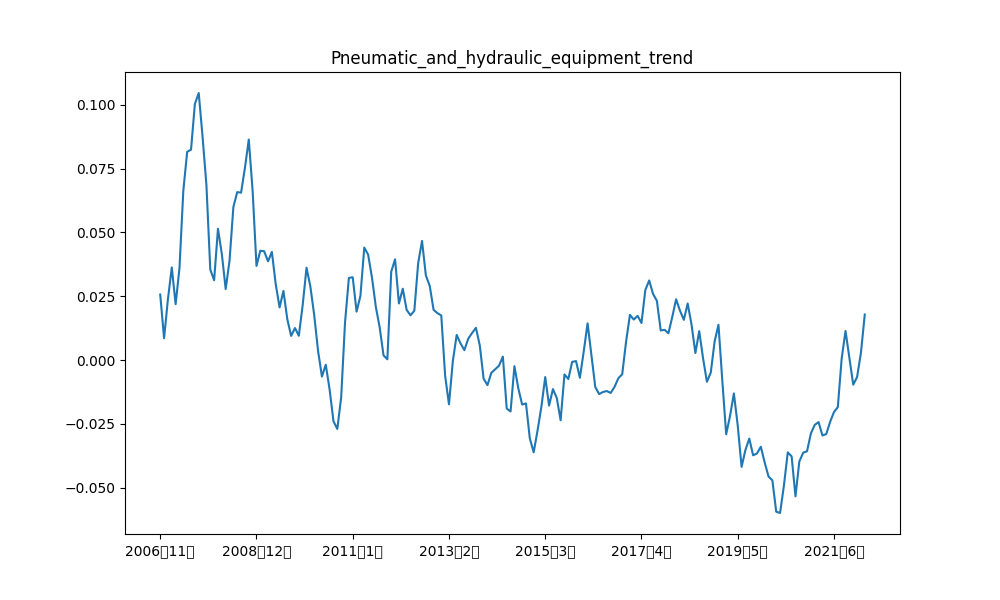
　これらの表を比較すると実際の受注金額と異なり、予測では8月の受注金額が全ての項目で減少していることが分かります。Timeを軸に相関を比較してみます。すると、日経平均株価、産業ロボット、風水力機械、運搬機械、冷凍機械は青色、つまり時間経過に対して負の相関があることが分かります。したがって、この負の相関が8月の受注が減少した1つの要因であると考えることができます。特に風水力機械については実際にトレンド成分を見ると、徐々に増加傾向にあることが読み取ることは可能ですが、負の相関を学習したことにより、実際の受注金額と異なり減少してしまったと捉えることができます。

　しかしながら、あくまで相関であり減少率の大きさには言及ができておりません。これは今回の例でいうとTransfomerの学習過程の可視化(Attentionスコアの変遷等)をする必要があり、学習モデルごとの実装が求められ、その点が今後の課題になります。

本記事のまとめ

本記事では時系列データ予測の結果を考察可能な実装方法として、季節性の分解、類似時系列の可視化、変化点検出、相互相関の可視化を実装してみました。そして前記事での結果を踏まえつつ可視化の結果を捉えることが可能かを検証しました。その結果、データの可視化から学習過程をある程度推測することが可能であることが分かりました。しかしながら、実際の学習過程がなければ把握できないこともあり、学習モデルに応じた学習過程の可視化が正確に説明するためには必要であることが分かったので、今後はその実装も考えていきたいです。また今後は、データ同士の因果関係を考察できるような実装もしていきたいです。

参考文献

〇学習データセット

• 機械受注統計調査 / 主要長期時系列統計表（2005/4～）
• 日経平均株価,時系列表,統計Dashboard

〇私の以前の記事

• 複数時系列データ × Transformerの実装と評価
• Pythonの時系列解析手法(SARIMA、LSTM、NeuralProphet)実装と比較
• 変動要因に類似点がある時系列データの需要予測に対する考察

〇本記事の目的の参考文献

• 機械学習における解釈可能性 (Interpretability) と説明可能性 (Explainability) のニュアンスの違い
• 機械学習チートシート

〇季節性の分解の参考文献

• (R編) 時系列データをサクッとSTLでトレンド・季節性に分解
• statsmodelsのseasonal_decomposeを活用した時系列データの可視化

〇類似時系列の可視化の参考文献

• color mapの一覧をheatmapで(160個くらい画像があるので注意)

〇変化点検出の参考文献

• 差分累積値に基づく農業環境データの可視化分析法,岩崎 清斗ら,2018
• 変化点検出を応用した時系列データからの突発現象の前兆検出アルゴリズム, 徳永 旭将ら,2011
• ruptures公式サイト
• Python ruptures でサクッと時系列データの変化点を見つける方法

〇相互相関の可視化の参考文献

• 自己相関関数と相互相関関数
• 相関係数とは何か。その求め方・公式・使い方と3つの注意点