Zenn
🤖

変動要因に類似点がある時系列データの需要予測に対する考察

2023/02/26に公開
Python
時系列解析
需要予測
tech

前記事のまとめ、および、本記事の目的

前記事(前記事url)では、以下ののデータセットと環境での構築を行いました。

  • データセット : Store Item Demand Forecasting Challenge
  • 実装環境 : google colaboratory
    　このデータセットを2013年～2017年までの各顧客の50品種の需要と読み替え、顧客No 1のうち需要予測を実施しました。まず、各品番の需要の推移をみると、数量の違いはあるものの、トレンドや周期が似ていることが分かりました。
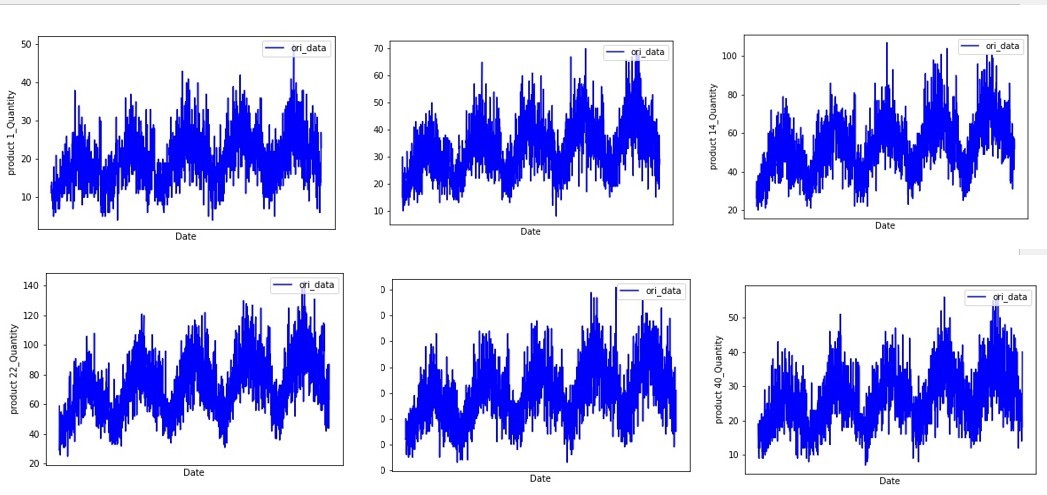
    各品種の需要推移
    そこで、product 1に対し2016年までのデータを訓練データとし、2017年の予測データの比較をしました。
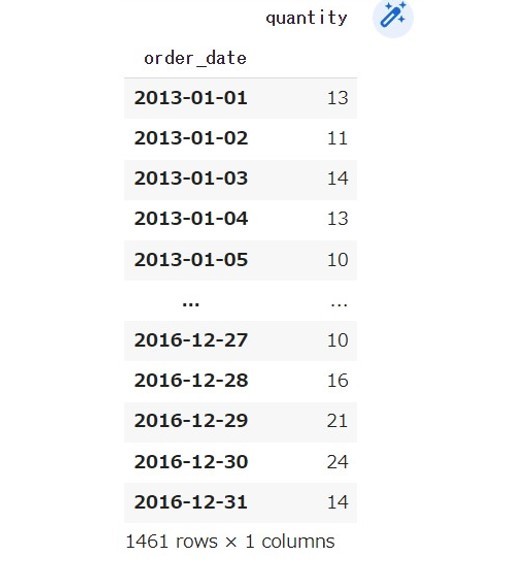
    訓練データ
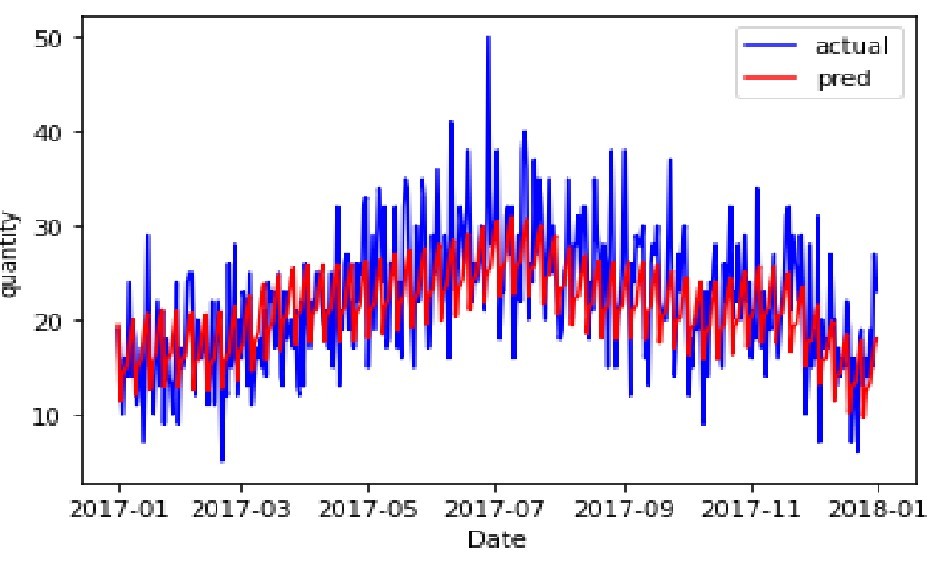
    NuralProphet
    　SARIMA、LSTM、NeuralProphetでの実装を行い、上図のNeuralProphetによる予測が今回のデータセットではよいという結果が得られました。しかしながら、product 1のみの比較であり、他の品種への流用方法は考えておりませんでした。そこで、本記事では、product 1の結果を異なる品種へ流用する方法を考えていきたいと思います。

時系列データ類似品種に対する需要予測方法の考察

今回考えた方法は以下の2点です。

  • 異なる品種に対してNeuralProphetを使用する方法
  • product 1と他品番の変動要因を比較する方法

異なる品種に対してNeuralProphetを使用する方法

時系列データが類似しているため、異なる品番にもNeuralProphetを利用すれば良い精度が得られるのではないのかと考えました。NeuralProphetを利用する方法として考えられる方法は、異なる品番に対し同じパラメータ候補で学習し直す方法と、product 1の最適パラメータを用いる方法があります。なお、実装方法やパラメータの候補については前述の前記事のNeuralProphetの節を参考にして頂ければと思います。

同じパラメータ候補で学習し直す方法

同じパラメータ候補で学習し直す方法は、確かにデータが類似しているのでNeuralPropphetを用いればよい結果を得られるかもしれませんが、各品番の学習時間が別途かかってしまうのが難点となります。品種数が少なければそれでよいとは思いますが、品種数が多くなれば全体の学習時間は増加してしまいます。また、最低限の担保を保つための学習時間を判断する工数もかかります。今回の作業を例に挙げると、探索時間は、

  study.optimize(objective_variable(train,valid), timeout=1000)
  optuna_best_params = study.best_params

上記timeoutで指定できます。ここで、timeoutを1000秒にした理由は、前記事のまとめのproduct 1の学習結果を導き出した2400秒から徐々に少なくしてみてMAEが大きくなりすぎない秒数を何度かやりお直してみて導出した秒数になります。

検索時間が1000秒だとしても、他49品種に適用すると、49,000秒(約13時間半)かかかります。今回product 2 ～ product 10までの9品種をやってみましたがそれでも2時間半かかってしまいます。またproduct 1でMAEが大きくなりすぎない秒数であっても、他品種で必ずしも良い精度がでるとは限らないようです。
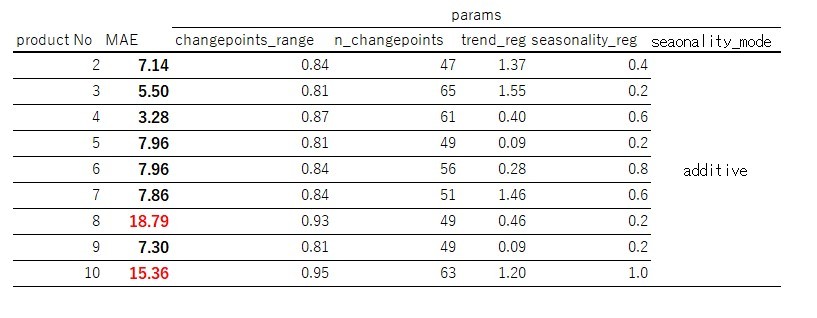
MAEとパラメータセット
例えば、product 4はMAE小さいですが、product 8やproduct 10はMAEが大きく予測グラフを見ても差分が大きくなっています。
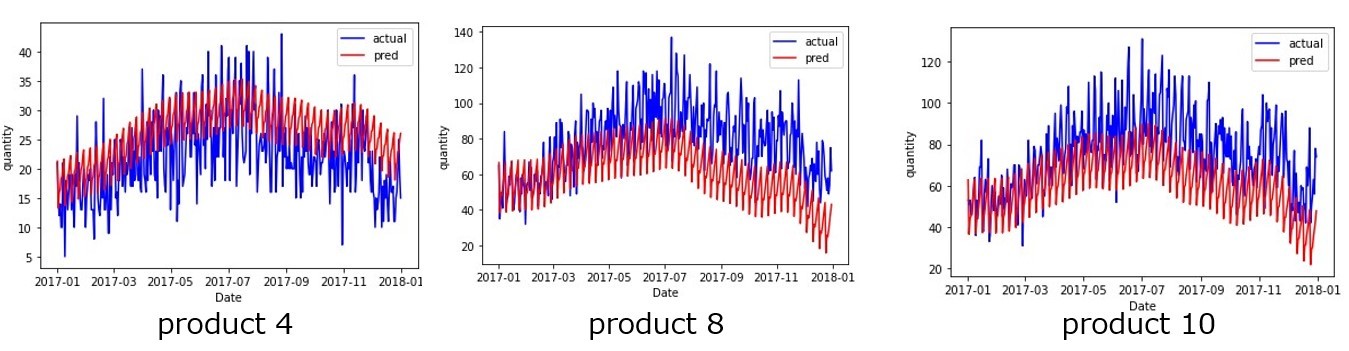
グラフ比較
　このように、同じパラメータ候補で学習し直す方法は、膨大な品種に対して一度に予測結果を出力しようという場合、工数(時間)・精度の両面で悪い結果になる可能性が高いと思われます。一方、精度は悪くなる可能性はあるものの、需要推移のトレンドや周期の表現はある程度はできているように見えるので、特定の品番のみを出力したいという場合や需要のトレンドや周期性を考える1つの判断材料として出力したい場合には有用な方法のように思います。

product 1の最適パラメータを用いる方法

続いて、product 1の最適パラメータを用いる方法について考えていきます。この方法はproduct 1で最適なパラメータさえ求めてしまえば、パラメータの学習時間はなくせることになります。なお今回のproduct 1の最適パラメータは、以下のようになっていました。

  • (changepoints_range, n_changepoints) = (0.92,64)
  • (trend_reg) = (0.63)
  • (seasonality_reg) = (0.0)
  • (seaonality_mode) = "additive"
    　上記の表を見れば分かるように最適パラメータは一致しているわけではないので差分が出る可能性もあります。例としてproduct 2を比較してみると、この方法では先程の方法より差分がでていることが分かります。
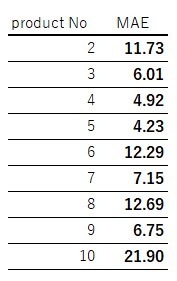
    同一パラメータのMAE
    探索方法による違い
    しかしながら、前述の通り、今回は各品種において上記パラメータで一度回すだけであり、約6分(約40秒(/品種) * 9品種)で予測値を出力することが可能です。このことから、工数の面で考えると、product 1の最適パラメータを用いる方法がよいです。また、同じパラメータ候補で学習し直す方法と同様、各品種における需要推移のトレンドや周期の表現はある程度できているようにみえます。
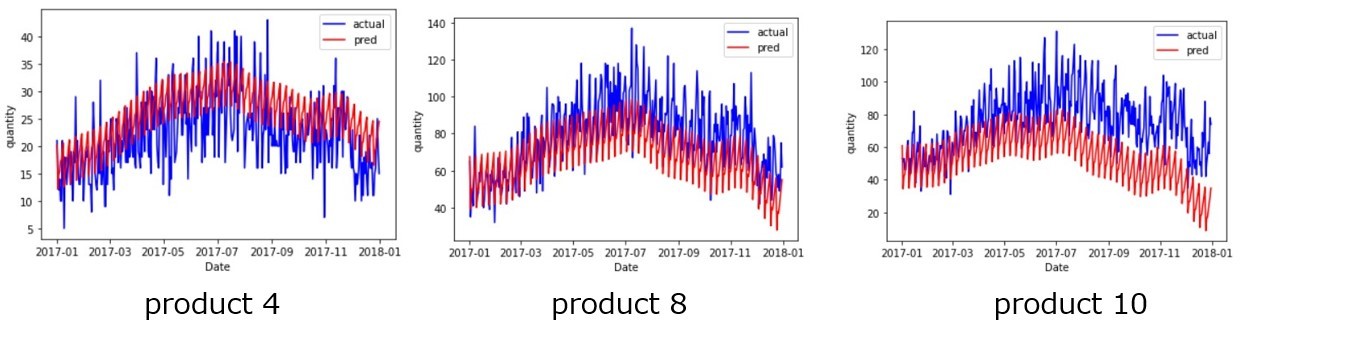
    同一パラメータ_比較
    　以上より、需要のトレンドや周期性を考える1つの判断材料として出力したい場合は、product 1の最適パラメータを用いる方法を用いるのが良いと考えています。

product 1と他品番の変動要因を比較する方法

前述の方法は、product 1以外の品番に対してもNeuralProphetで学習しないといけない都合上、どうしても学習時間がかかってしまいます。しかしながらトレンドや周期が似ている品種に対して、何度も学習時間をかけることは工数の面で改善できる点であるのではないか考えました。そこで、まず類似点を抽出し特定の処理を加えるにより、基準となる品種(今回の例ではproduct 1)の予測値を利用した上で、工数を削減し良い精度も得られる方法を考えていきたいと思います。
　まず、今回のデータセットにおいて、各品種のトレンドや周期に類似点が見受けられることは既に述べているが、実際にグラフで見ていきます。変動要因の除去や描画は、statsmodelsライブラリのseasonal_decomposeを行うことが可能で、トレンド、周期、誤差を分解できます。なお、顧客No.1のデータフレームを「df_company1」としており、品種名はprouct_nameに格納されています。

import statsmodels.api as sm

period = 365 #1年周期
pn_list = list(df_company1["product_name"].drop_duplicates())
for pn in pn_list :
　　#品種別の[日付(インデックス),数量]のデータフレーム作成
  querystr = 'product_name == "' + pn + '"'
  df_target = df_company1.query(querystr)
  df_target = df_target.sort_values(by='order_date', ascending = True) 
  df_target = df_target.groupby('order_date').sum().reset_index()
  df_target = df_target.set_index("order_date")
  #トレンド・周期・誤差の分解
  res = sm.tsa.seasonal_decompose(df_target,freq=period)
  #グラフ描画
  fig = res.plot()

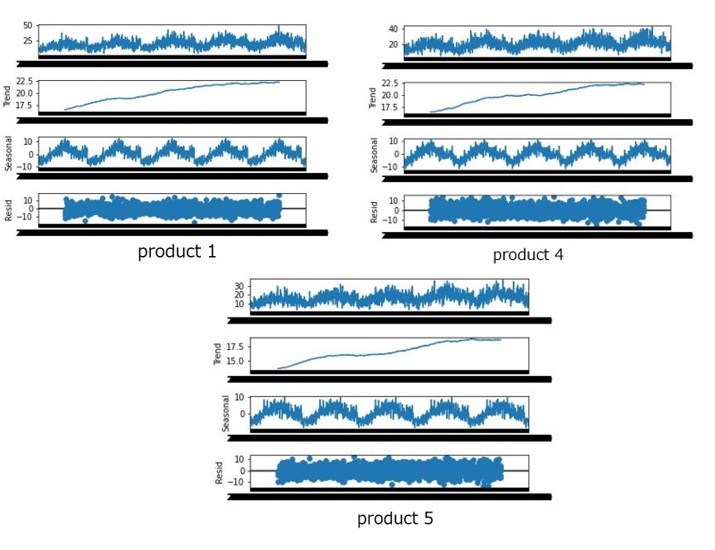
実際の分解結果例として、何品種か結果を挙げます。
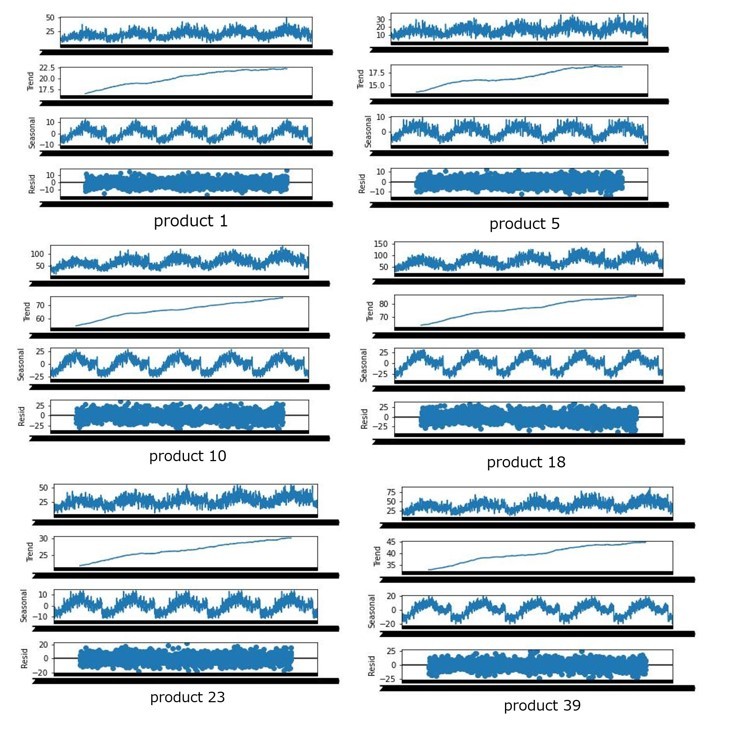
変動要因の比較

上図から分かるように品種毎の各変動要因のグラフの推移が類似していることが分かります。一方、各変動要因の値は品種毎に差分が大きいことが読み取れます。このことから、類似性のある品種とは、基準となる品種に対し各変動要因の推移が類似しており、各変動要因の変化量よりも、各変動要因に対する差分の影響が大きい品番であると捉えられると考えました。この考えを今回の予測方法の実装に生かしていきたいと思います。
上図から分かるように各品種においてトレンド・周期・誤差のグラフの推移が類似していることが分かります。一方、各変動要因の値は各品種で差分が大きいことが読み取れます。このことから、類似性のある品種とは、基準となる品種に対し各変動要因の推移が類似しており、各変動要因に対する差分の影響が大きい品番であると捉えられると考えました。この考えを今回の予測方法の実装に生かしていきたいと思います。
　基準となる原系列OP(t)は、トレンド成分T(t) 、周期性成分S(t)、誤差成分e(t)の和で算出できます。同様に、類似性のある品種nの原系列OPn(t)は、トレンド成分Tn(t)、周期性成分Sn(t)、誤差成分en(t)の和で算出できます。類似性のある品番のうち、基準となる品種の各変動要因の推移が似ているという性質を、時刻tに対する各変動要因の変化量が小さいという性質があると捉えます。つまり、変動成分のうち時刻tの変数部分は、基準となる品種とほぼ同じと捉えることとします。この性質を考慮した上で、変動要因に対する差分が原系列に影響が大きいという性質を表すために、変動成分を平行移動させて時刻毎の成分の値を増減させることで表現しようと考えました。例えば、トレンド成分がtの1次関数で表現される場合、時刻tに対する各変動要因の変化量が小さいという性質は、トレンド成分T(t)とTn(t)の傾きが等しいと捉えます。そして、変動要因に対する差分が原系列に影響が大きいという性質は、基準となるトレンド成分T(t)に対してy軸方向にmだけ平行移動させて、このmが原系列に影響を及ぼしていると捉えることとします。イメージ図は下記の通りです。
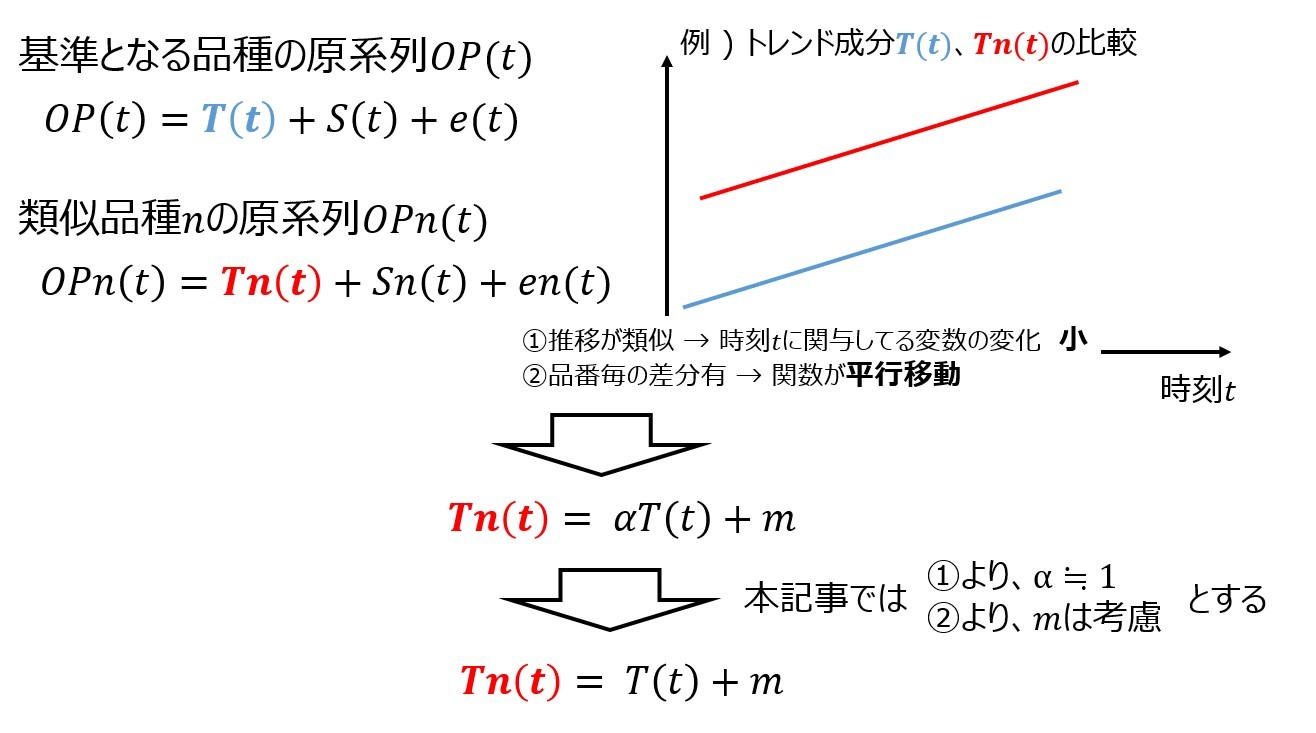
類似品種の成分の考え方
同様に周期成分、誤差成分の平行移動の量をn、lとし、OPn(t)を以下のように表します。
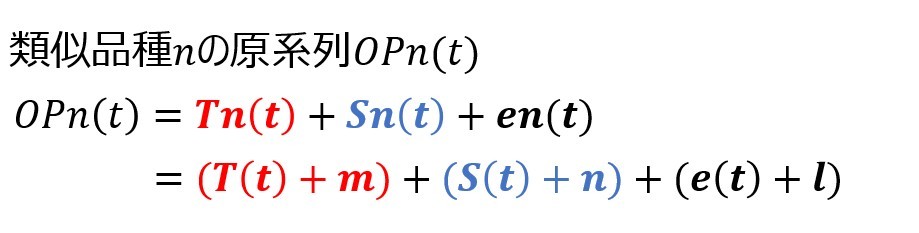
類似品種数式
　この数式を基に品種毎の2017年度の需要を算出します。以下の手順で求めていきます。

  • STEP1 : 基準となる品種における過去データ(今回は2016年まで)の各変動要因の成分を抽出
  • STEP2 : 類似品種における過去需要量の抽出
  • STEP3 : 平行移動量m、n、lの算出
  • STEP4 : 基準となる品種における将来データ(今回は2017年)の各変動要因の成分を抽出
  • STEP5 : STEP4の各成分にSTEP3の値を足して、類似品番における将来データの需要を算出
STEP1の実装

まず基準となる品種の2016年までの各変動要因の成分を抽出します。seasonal_decomposeで成分の抽出をすると、トレンドや誤差においてNan(値なし)で表現される日付があります。
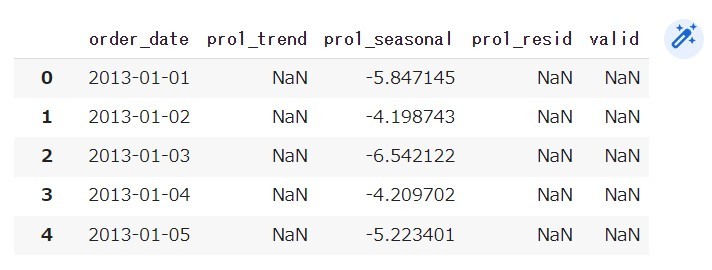
STEP1のNan例
各成分は日付と1対1で対応しているため、成分毎にNanを除去すると、成分毎に日付のズレが生じる可能性があります。そこで、基準となる品種の各成分、STEP2とSTEP3で使用する需要量を格納するデータフレーム「df_pro_seasonal_decompose」を作成します。実装方法は以下の通りです。

df_pro_seasonal_decompose_STEP1.py
#df_pro_seasonal_decompose内容
#order_date : 日付
#pro1_〇〇 : 基準となるproduct 1の各成分格納列
valid : 平行移動量(m,n,l)を算出時使用する過去需要量
df_pro_seasonal_decompose = pd.DataFrame(columns=["order_date","pro1_trend","pro1_seasonal","pro1_resid","valid"])

#基準となる品種の元データフレーム : df_target(列 order_date, quantity)
querystr = "product_name == 'product 1'" #基準品種 product 1
df_target = df_company1.query(querystr)
df_target = df_target.sort_values(by='order_date', ascending = True) 
df_target = df_target.groupby('order_date').sum().reset_index()
df_target = df_target.query("order_date <= '2016-12-31'")
df_target = df_target.set_index("order_date")

#product 1のトレンド・周期・誤差の抽出
res_pro1 = sm.tsa.seasonal_decompose(df_target,freq=period)

#日付・トレンド・周期・誤差の格納
df_pro_seasonal_decompose["order_date"] = res_pro1.trend.index
df_pro_seasonal_decompose["pro1_trend"] = res_pro1.trend.values
df_pro_seasonal_decompose["pro1_seasonal"] = res_pro1.seasonal.values
df_pro_seasonal_decompose["pro1_resid"] = res_pro1.resid.values
STEP2の実装

続いて、過去需要をvalid列に格納し、Nanの除去をしていきます。なお、実装をする際、各品種でfor文を回したりして繰り返し行うことを考え、df_pro_seasonal_decomposeのコピーを取る実装を記載しておきます。

df_pro_seasonal_decompose_STEP2.py
df_pro_seasonal_decompose_copy = df_pro_seasonal_decompose.copy()
 df_pro_seasonal_decompose_copy["valid"] = list(df_target["quantity"])

ここまでで、df_pro_seasonal_decompose_copyの全ての列を格納できたので、NA存在行の削除と抽出をしていきます。

pre1list_valid_STEP1_2.py
#NA存在行削除
df_pro_seasonal_decompose_copy = df_pro_seasonal_decompose_copy.dropna()

#訓練データ(2016年までのproduct 1の成分抽出) ※今回は最後1年周期分で行ってみました
pro1_trend = list(df_pro_seasonal_decompose_copy[-period:]["pro1_trend"])
pro1_seasonal = list(df_pro_seasonal_decompose_copy[-period:]["pro1_seasonal"])
pro1_resid = list(df_pro_seasonal_decompose_copy[-period:]["pro1_resid"])

#検証データ(類似品番の1年周期分の需要量)
valid = list(df_pro_seasonal_decompose_copy[-period:]["valid"])
STEP3の実装

最適な平行移動量の探索方法には、optunaライブりを使用して実装する。具体的には、2016年までの基準となる品種のトレンド成分(pro1_trend)、周期成分(pro1_seasonal),誤差成分(pro1_resid)に対し、平行移動の候補値を加算し、類似品種の値となる予測値を算出します。この値をvalidと比較して差分の小さくなった、平行移動の候補値を採用します。差分の評価として今回はMAEを用いています。

Translate_params_STEP3.py
def Tranlate_pred(trend,season,resid,valid) :

  def objective(trial) :
    #最適パラメータ候補設定
    params ={
        "m" : trial.suggest_float('m',-30,70),
        "n" : trial.suggest_float('n',-20,35),
        "l" : trial.suggest_float('l',-20,35)
    }
   #平行移動分を考慮した予測値の算出
    pred = (np.array(trend) + params['m'] + 
           np.array(season) + params['n'] + 
           np.array(resid) + params['l'])

    #valid(2016年までの需要量との差分比較
    MAE = mean_absolute_error(valid,pred)
    return MAE
  
  return objective

そして、最適パラメータの学習の関数は以下のように実装できます。

Study_STEP3.py
def optuna_Translate(trend,season,resid,valid):
  study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
  study.optimize(SimimarRatio(trend,season,resid,valid), n_trials=1800)
  optuna_best_params = study.best_params
  return study
STEP4の実装

STEP4では基準となる品種であるproduct 1の2017年の予測データから各成分を抽出します。基本的には、df_pro_seasonal_decompose_STEP1.pyと同じ実装方法でよいですが、STEP1で述べたようにNanで表現される日付があるため、2017年の365日分の各成分の抽出ができるように、2018年の日付まで予測を行いました。(今回は念のため多めに2018/7/4までのデータを予測値として算出しました)NeuralProphetの予測において、予測期間の設定は、前記事より以下のコーディングにおける色付け部分のperiodの設定で変更することができます。

NeuralProphet_pred_STEP4.py
#パラメータ設定
m = NeuralProphet(
        changepoints_range = 0.92,
        n_changepoints = 64,
        trend_reg = 0.63,
        yearly_seasonality = True,
        weekly_seasonality = True,
        daily_seasonality = False,
        seasonality_reg = 0.0,
        epochs = None,
        batch_size =  None,
        seasonality_mode = 'additive')

#学習データセット
df_target = df_company1.query('product_name == "product 1"') #基準となる品種 product 1
df_target = df_target[["order_date","quantity"]]
df_target = df_target.query("order_date <= '2017-12-31'")
data = df_target.rename(columns={'order_date': 'ds', 'quantity' : 'y'})
train = data[data['ds'] <= '2016-12-31']
valid = data[(data['ds'] >= '2017-01-01')&(data['ds'] <= '2017-12-31')]

#日毎の予測
metric = m.fit(train,freq="D")

#予測値の格納
+ future = m.make_future_dataframe(train, periods=550)
forecast = m.predict(future)
pred = forecast[['ds','yhat1']]

このようにして求めた予測値に対して、df_pro_seasonal_decompose_STEP1.py同様成分の格納をしていきます。

df_pred_seasonal_decompose_STEP4.py
period = 365

#product 1のトレンド・周期・誤差の抽出
res_pred = sm.tsa.seasonal_decompose(df_pred,freq=period)

#日付・トレンド・周期・誤差の格納
df_seasonal_decompose = pd.DataFrame(columns=["order_date","pred_trend","pred_seasonal","pred_resid"])
df_seasonal_decompose["order_date"] = res_pred.trend.index
df_seasonal_decompose["pred_trend"] = res_pred.trend.values
df_seasonal_decompose["pred_seasonal"] = res_pred.seasonal.values
df_seasonal_decompose["pred_resid"] = res_pred.resid.values

#2017年分のデータフレームdf_2017
df_2017 = df_seasonal_decompose.query(("order_date >= '2017-01-01' & order_date <= '2017-12-31'"))

#2017年のproduct 1の各成分pred_〇〇
pred_trend = list(df_2017["pred_trend"])
pred_seaonal = list(df_2017["pred_seasonal"])
pred_resid = list(df_2017["pred_resid"])
STEP5の実装

STEP3とSTEP4における算出値や格納リストを使って2017年の類似品種の需要を算出します。

2017quantity_STEP5.py
pred = (np.array(pred_trend) + study.best_params['m'] + 
        np.array(pred_seaonal) + study.best_params['n'] + 
        np.array(pred_resid) + study.best_params['l'])

各手法の評価

以上の3手法に対して評価をしていきます。同じパラメータ候補で学習し直す方法を①、product 1の最適パラメータを用いる方法を②、product 1と他品番の変動要因を比較する方法を③とし、MAEと予測時間を比較していきます。なお、予測時間に関しては、①と②は時間の都合上、49品種全て行わなかったので、あくまで推定時間となっております。また、各項目の最小値を青太字、最大値を赤太字で表現しています。
MAEと予測時間比較
　①はMAE最小値が最も多い反面、予測時間が膨大となっています。また、前節でも述べましたが、②は①と比較して、精度が悪くなりますが、工数の面では大幅な改善が見込まれます。一方、②がMAE最小値となっている品種も①と同程度存在し、一概に精度が悪いとは言えません。予測出力時間が圧倒的に少ない③は、良い精度・悪い精度も同程度存在し、①と②の中間の精度のように見えます。
　③で最も悪い精度であるproduct 18を見てみると、周期を上手く表現できておらず予測値がほぼ一定になってしまっていることが分かります。
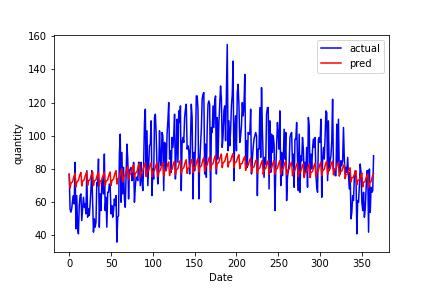
product18_③
一方、③の中で良い精度の品種を見てみると、周期性が上手く表現されている結果、予測値の差が減少しています。
product比較
変動要因の分解グラフを見てみると、product 1、4、5の誤差が-10～10の定常状態のグラフになっており、このことから、誤差成分の類似性がある品種、つまり、定常性のあるグラフにした際に類似性がみられる品種は、平行移動の考え方が使えるのではないかと考えました。
変動要因v2
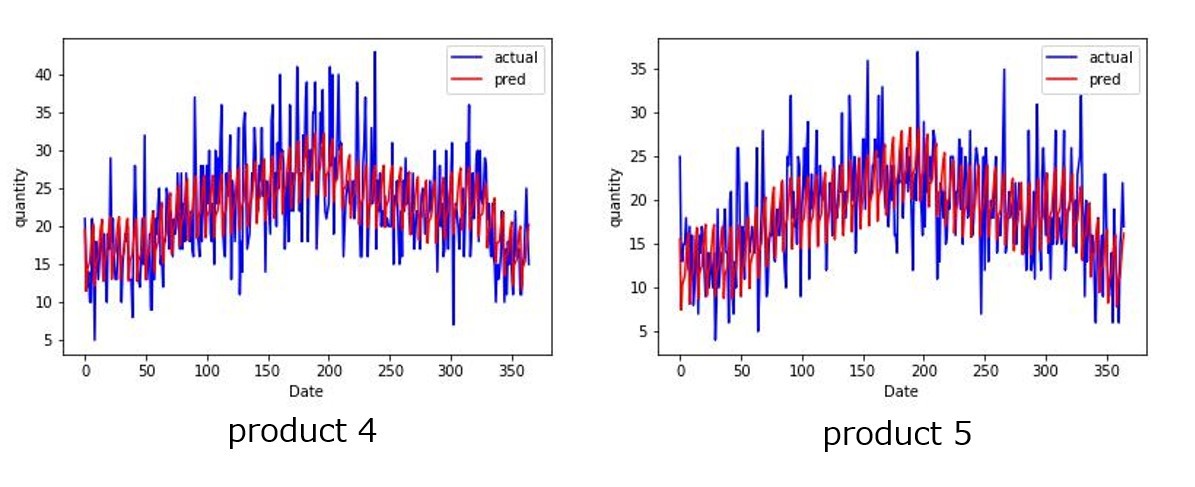
　また②で良い精度も悪い精度も存在している理由も、product 1基準で考えており、定常性のあるグラフにした際、類似している品種と類似していない品種が存在していることが一因でないかと思いました。実際、②でMAEが小さい組はproduct4とproduct 5です。
　以上の考察より、基準となる品番の組を作成し、基準となる品種において機械学習を使い予測値を求め、定常性の類似性が認められる品種において平行移動の考え方を用いることが、精度・時間の両面で良い手法で考えられます。

本記事のまとめと次回記事内容(予定)

本記事では、開発工数のかからない多品種少量生産下の需要予測手法の確立を目指し、ある1品種を基準品種とし、その品種の予測値の算出方法・算出値を流用した他品種への需要予測方法の考察を実施しました。今回は、予測値の算出方法・算出値を流用した方法として、基準品種produt 1で最も良い結果を導出したNeuralProphetを用いた方法、product 1と他品種の変動要因の差から考える方法を考え評価しました。その結果、誤差成分に類似性がある品種を分類し平行移動と組み合わせれば工数・精度の両面で良い手法ができるのではないかと考えました。
　そこで、次記事では誤差成分グラフの分類問題を機械学習を用いて行える手法を考えていきたいです。

参考文献

〇前記事
・Pythonの時系列解析手法(SARIMA、LSTM、NeuralProphet)実装と比較

〇seasonal_decomposeについて
・statsmodels.tsa.seasonal.seasonal_decompose

〇optunaについて
・Optimize Your Optimization
・optuna.trial.Trial

〇pandas取り使いの参考資料
・pandasクックブック ―Pythonによるデータ処理のレシピ(書籍、Amazonurl)

Discussion