👋

複数時系列データ × Transformerの実装と評価

2023/11/10に公開

4件

本記事の動機
時系列解析とTransformerに対する先行研究のまとめ
複数時系列データの解析に対する課題を解決した改善モデル iTransformer
iTransformerモデルの実装
実装環境と学習データ
データの前処理
iTransformerモデル実装と最適パラメータ探索
数値実験と考察
本記事のまとめ
参考文献

本記事の動機

近年ではビックデータの利活用が活発になっており、データを蓄積・分析することが多くなっています。その際、機械学習やAIの実装をしてデータの分析を行う場合、データ数が鍵となっています。しかしながら、データの項目数が多いと、各項目のデータ数が少なくなる可能性があります。例えば、ある市場で売られている品種が複数あった場合、受注数の差だけではなく、受注のデータ数にも差が生じ、結果的に分析に使用可能なデータ数が少なくなり、分析の精度が低下することが考えられます。他方で、各項目のデータには相関があることがあります。例えば、ある品種Aの受注が増加した場合、異なる品種Bの受注が増加するという事象や、ある市場が低迷している際は、品種Aの受注が落ちるといった事象です。そこで、項目間の相関を考慮に入れつつ分析を実施することで、項目ごとのデータ数が少なくても分析が可能ではないかと考えたことが、本記事の動機です。

時系列解析とTransformerに対する先行研究のまとめ

本記事では、項目間の相関を考慮に入れた分析の1つとして、時系列解析による予測を扱います。
　時系列解析による予測は、ARIMA、SARIMA、RNN、LSTM、NeuralProphetなどによる実装が可能です(参考記事1、参考記事2、参考記事3、参考記事4)。これらの記事では、株価や受注等1変数で分析を行っていますが、項目間の相関を考慮する際は、多変数での分析が求められます。多変数の分析は重回帰分析、ARIMAを多次元化したVARMAモデル(参考書籍1)、回帰分析とLSTMを組み合わせて多変数を考慮して時系列解析をする手法などがあります(参考論文1)。しかしながら、ARIMAのようなモデルは、受注など多様な要因によって変動するものに対しては、その要因全てを反映させることが困難です(参考論文2)。また、LSTMなどのようなモデルは、逐次的に過去の値を参照しており過去データを直接参照できないという問題や、学習するための層がブラックボックス化しており、項目間の相関が分からないという課題がありました(参考論文2、参考論文3)。
　そのような中で、自然言語処理の分野で、データを再帰的に参照するモデルとして、Transformerと呼ばれるモデルが提案されました(参考論文4)。Transformerは、ChatGPTの基礎となっているモデルで、self attentionと呼ばれる機構を実装しています。この機構は、入力したデータに対して、トークン化をして、どの部分に着目すべきかを重みづけをすることで結果となるトークンを出力する機構になっています。(参考書籍2,参考書籍3)。
　具体的には、各トークンをクエリ、キー、バリューの3つのベクトルに分解します。クエリは入力値で、機構を用いた計算による出力として期待される値です。キーは、トークン同士の関連性の測定時に扱う値で、クエリとの内積により類似度を算出し、各トークンがどのトークンに関連性があるかを算出する値です。バリューは出力値で、前述の類似度を使って重みづけをしていき更新をすることで、最終的に利用する値になります(参考記事5、参考動画)。下図はイメージです。食材の買い物を例にすると、必要な食材のリスト(クエリ)に対して、食材の認識番号であるラベル(キー)を見ていき、必要な食材であるかを判断(類似性を算出して重みづけ実施して値を更新)して、実際に買い物かごに入れる(バリューを算出)イメージです。(参考書籍2、参考記事6)。
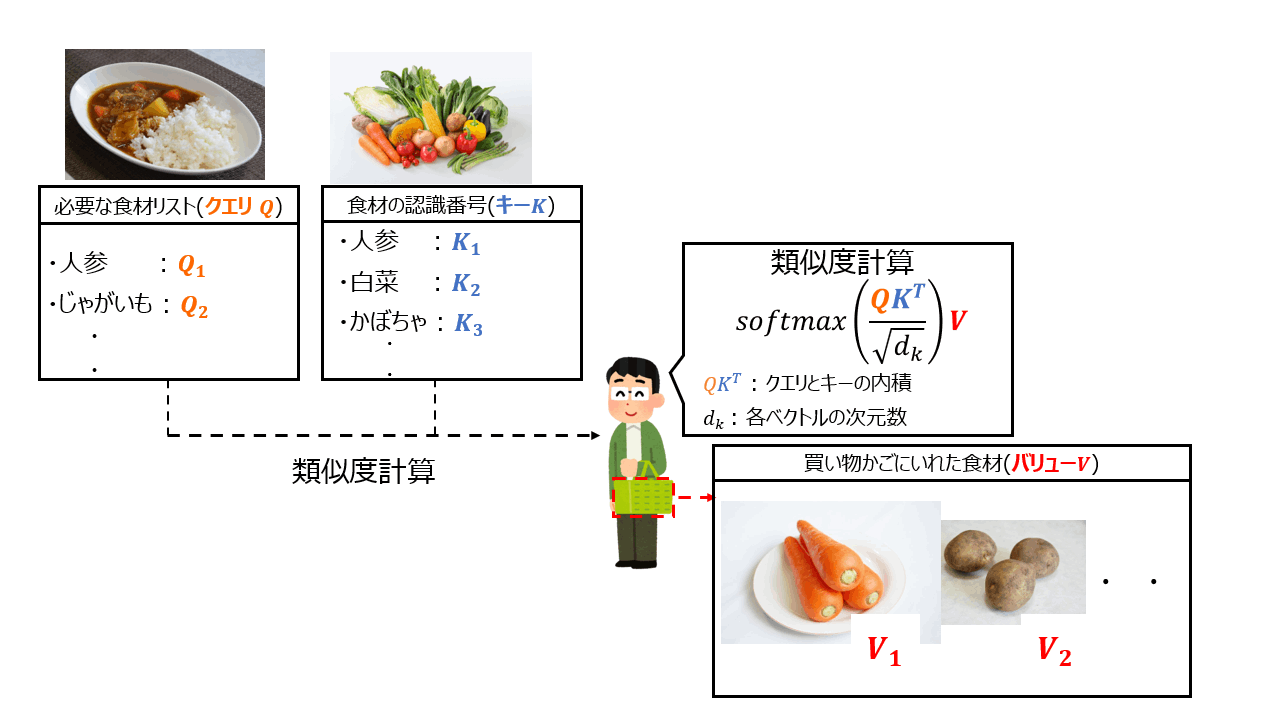
selfattentionイメージ図
　実際にはこのself attention機構を同時に複数適用させて、複数のクエリ、キー、バリューを作成し、有用な情報を取得します(Multi-Head Attention)。また、Transformerでは、位置エンコーディング(Position Encoding)と呼ばれる、各トークンに対する相対位置を数値化し、埋め込みベクトルに加算した上で、self attentionに適用します。これにより、各トークンの位置情報を加味した学習が可能となります(参考記事6)。
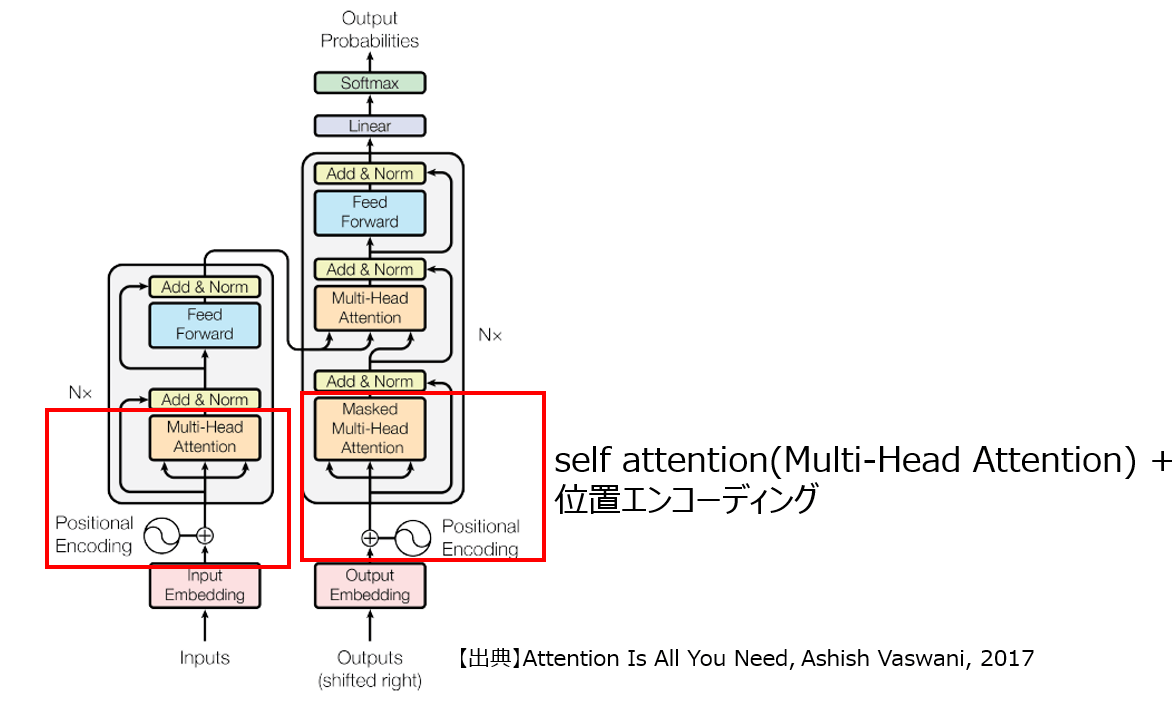
Transformerのアーキテクチャ
これらを組み込んだアーキテクチャを構築することで、自然言語処理としては、文脈を考慮する学習を可能にし、機械翻訳などで有用な手法になっています。
　他方、自然言語処理における機械翻訳について、各トークンを各時刻の数値、文脈への考慮を各時刻間の関係性の学習、翻訳結果を時系列予測と捉えることで、自然言語処理を時系列解析に利用可能と考えられます(参考論文5)。
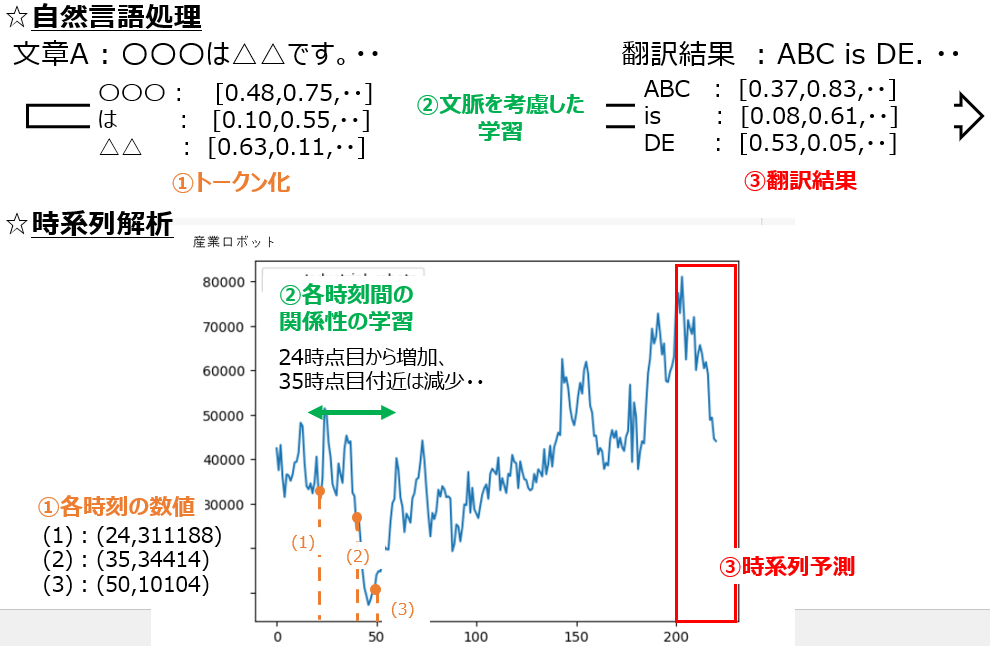
自然言語処理と時系列解析の関係性
実際Transformerを用いて、インフルエンザの感染者の予測を行い、他の時系列モデルより有用な結果が得られています(参考論文6)。また、複数の言語を使用することで情報の補完や曖昧性を解消させることにより、1つの言語への機械翻訳を実現可能です。これを時系列解析に置き換えると、複数の時系列データから相関などの関連性を整理し、予測結果を出力可能であることを示唆しています(参考論文5、参考論文7)。
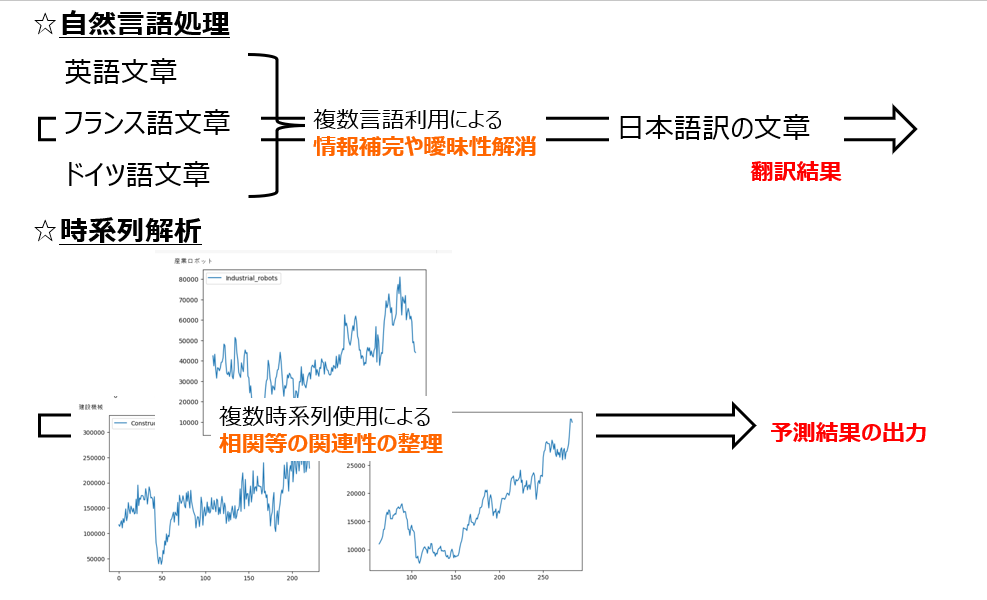
複数言語の機械翻訳と多変数時系列からの予測の関係性
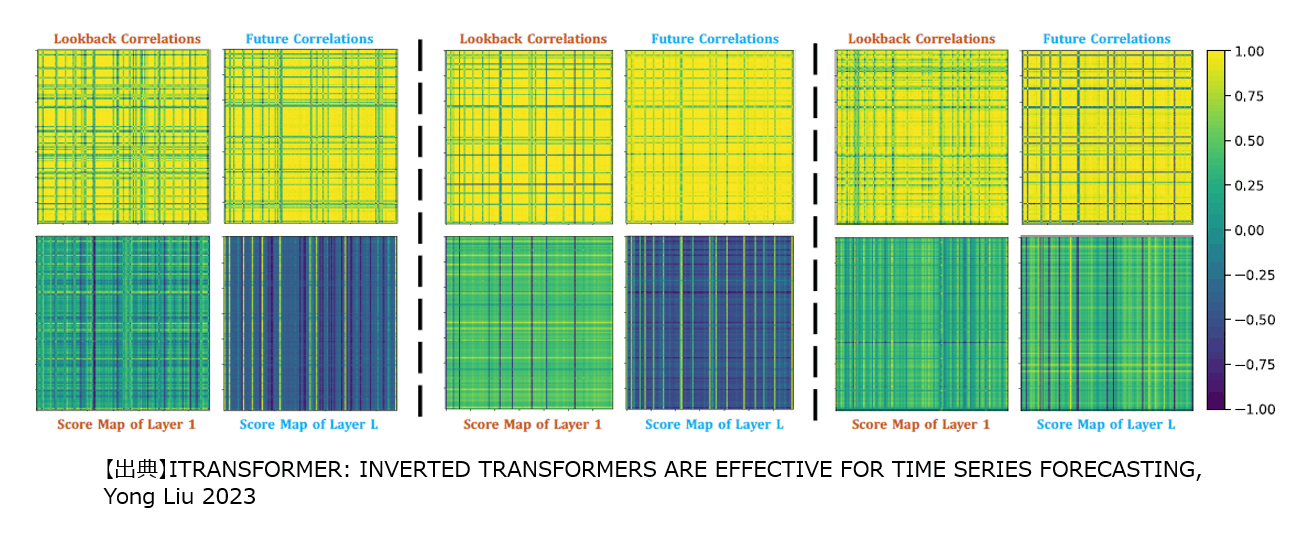
　参考論文2では、まず、1つの時系列データにおける各時刻の値をself attentionを用いて学習させます。これにより、1つの時系列データにおいて、過去のどの時刻の値と関連性があるかを算出させ、各時刻との関連性の重要度を出力します(論文中では、Time Transformerと呼んでいます)。
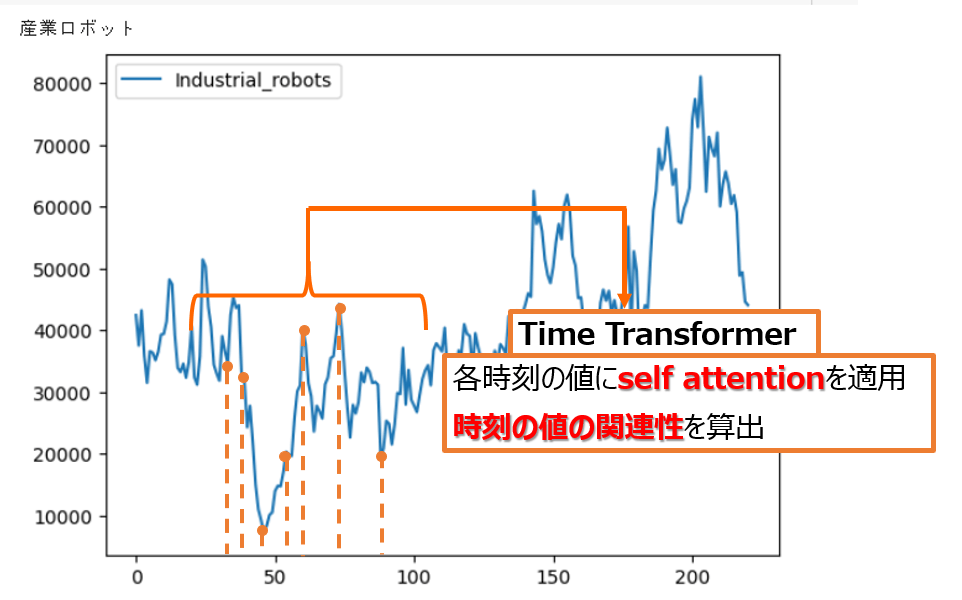
TimeTransformerイメージ図
　次に、各時刻における時系列データ同士に対してself attentionを用いて学習させることで、同時刻間の時系列データ間の関連性を算出します(論文中では、Space Transformerと呼んでいます)。
SpaceTransformerイメージ図
　この2つのTransformerを繰り返し行うモデルを実装し、各時系列の相関を導出し時系列予測を行っていました、しかしながら、事前に実験をした結果誤差が高い結果になってしまいました。

複数時系列データの解析に対する課題を解決した改善モデル iTransformer

Transformerを用いた多変数の時系列解析で、上述のような結果になる要因を考察し、多変数での時系列解析に適したモデルとして提案されたのが、iTransformerになります(参考論文8、参考記事7)。
　この論文を読み、上述の実装を含めた多変数におけるTransformerの実装の課題点は2点あると考えました。
　1点目は、時系列データの関連性を算出する際に、各時刻の値でトークン化していた点です。これにより、時系列データ全体で考えた時に本来あるはずだった相関を上手く捉えることができない状態で学習がなされていました。iTransformerではこの課題を解決するために、時系列データ全体をトークン化することで、精度を向上させています。
改善点1
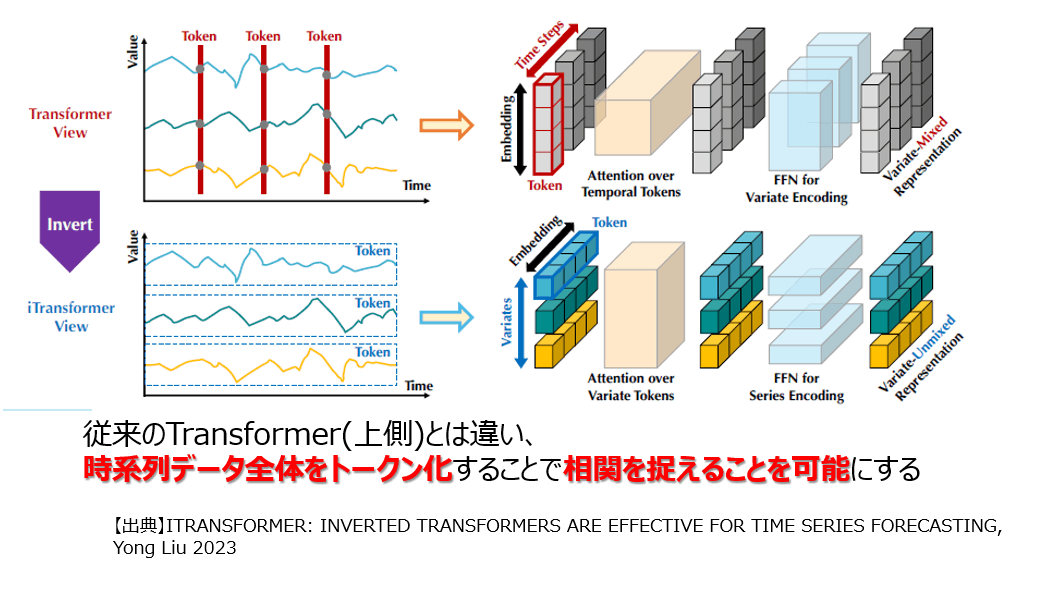
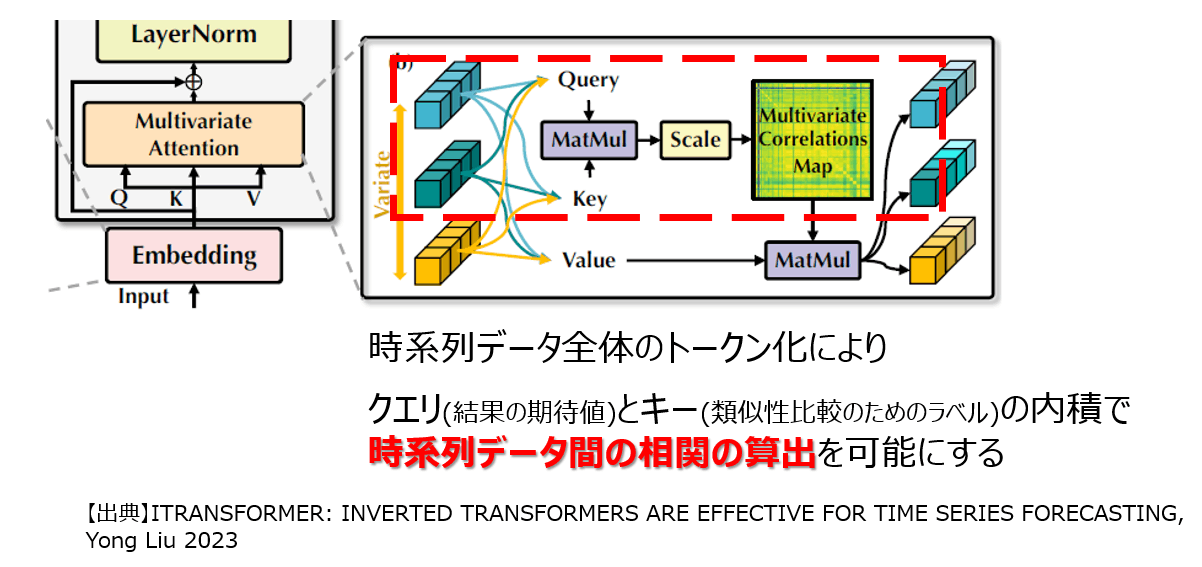
　2点目は、クエリとキーで類似性を算出する際に、時系列データに対する相関を組み込めていなかった点です。1点目の改善により、時系列データ全体をトークンとして考慮が可能になりました。これにより、類似計算におけるクエリとキーの内積が、時系列データ同士の相関、つまり、変数間の相関を出力するものとなりました。結果として、予測期間の時刻に対して、有用な情報を保持しながら、重みづけをして最終的な出力であるバリューの更新を可能としています。
改善点2

iTransformerモデルの実装

実装環境と学習データ

それでは上記改善モデルであるiTransformerの実装をしていきます。モデルの実装はGitHubにモデルの実装がなされていたので、そちらを参考にしました。実装はGoogle Colaboratoryで行い、データは政府統計ポータブルサイトであるe-Statと統計ダッシュボードのデータを使用しました。具体的には、機械受注統計調査、および、日経平均株価のデータを使用しました。また、後述の通り対数変換や階差などによる加工を実施しています。
　まず、機械受注統計調査のデータのうち、産業機械に割り当てられている項目をデータフレームに保存します。

machinary_orders.py

import pandas as pd

#機械受注長期時系列
machinary_order_data = r'/**/machinary_order_data.csv'
df_machinary_order_data = pd.read_csv(machinary_order_data)

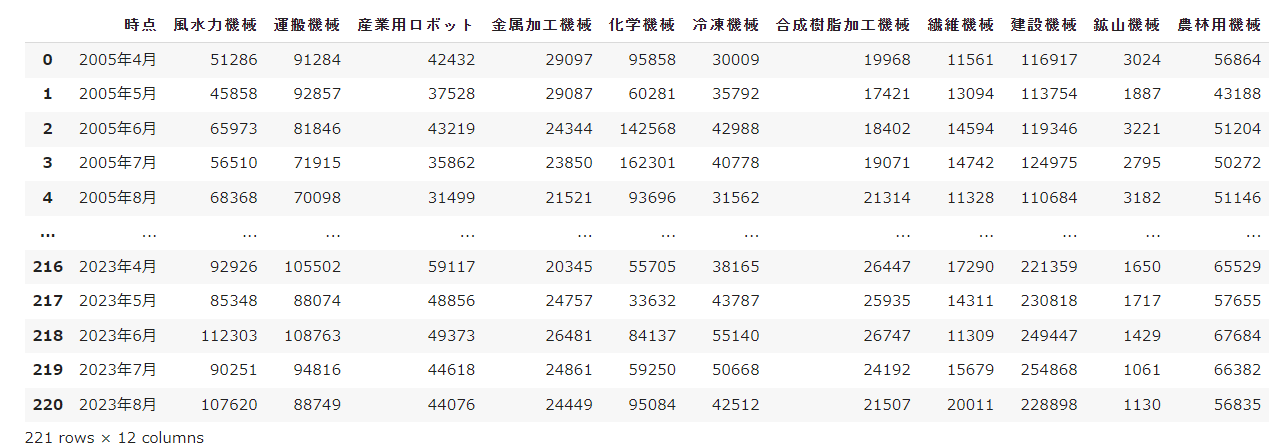
　本記事では、時系列データの数を増やす、および、相関がありつつ上記受注データとは異なるデータを付与する目的で、日経平均株価のデータを学習データに加えます。なお、機械受注データが、2005年4月～2023年8月のみ月次データだったので、その部分を抽出します。

stock.py

#日経平均株価
stock_data = r'/**/stockpredict/stockdata.csv'
df_stock = pd.read_csv(stock_data)[63:-1] #2005年4月～2023年8月

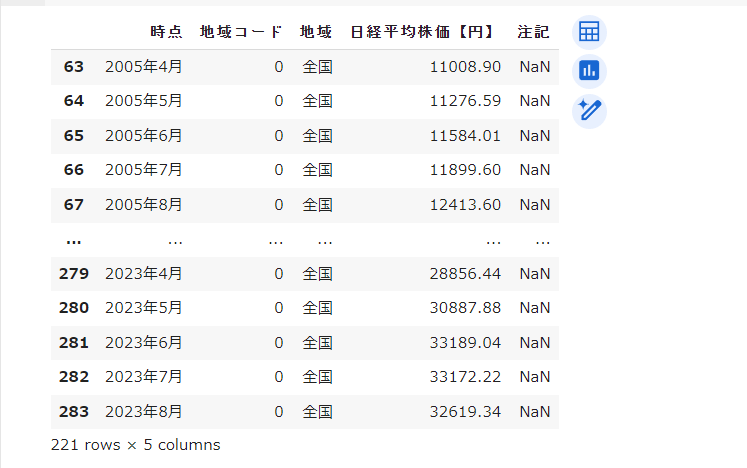
日経平均株価
　続いてmatplotlib.pyplotをインポートして描画します。結果例は以下の通りです。
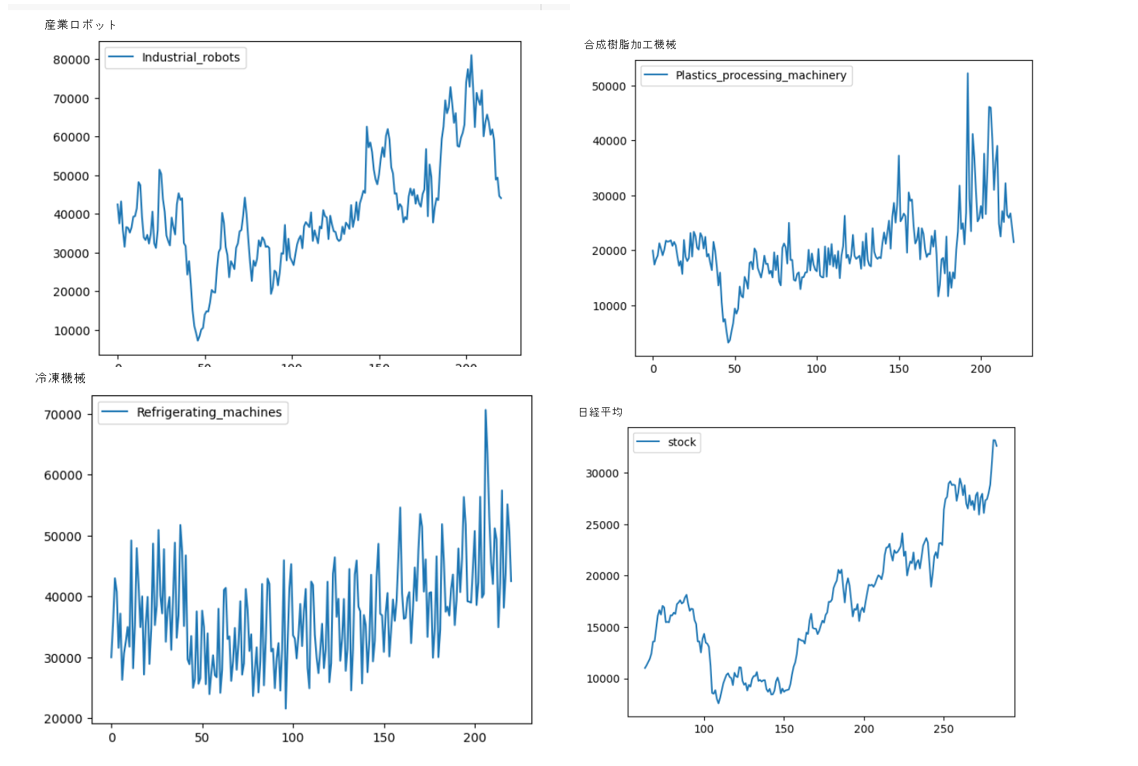
使用時系列例
　論文では、異なる相関を学習させないためか、時系列の傾向に類似性があるデータセットを使っているケースも存在したので(参考論文9)、明らかに傾向が違うデータは抜きました(例鉱山機械の受注)。
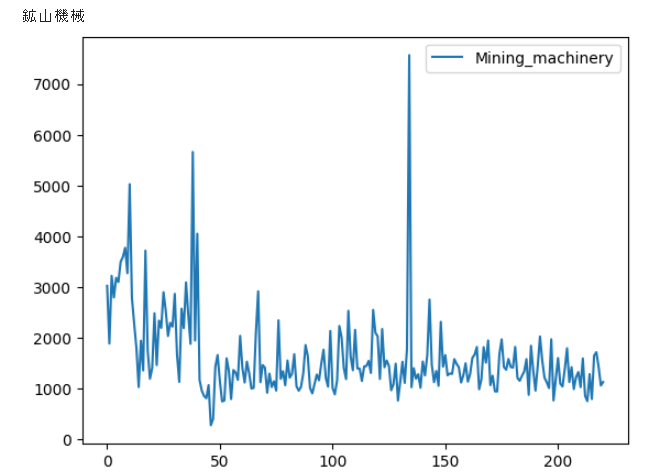
未使用時系列例
　以上より、使用するデータは、機械受注統計のうち、産業用ロボット、風水力機械、運搬機械、金属加工機械、冷凍機械、合成樹脂加工機械の6つと、日経平均株価の合計7つの2005年4月～2023年8月までのデータとします。

データの前処理

論文のデータセットをみると定常性がなさそうなデータでの予測になります。しかしながら、データセットの時系列数は137が多いものとなっていました。他方、データセットの中には、定常性があるデータもありました(参考論文9)。そこで本記事では、定常性のあるデータセットににして精度向上を試みました。具体的には、log10で対数変換をした後に、階差を取りました。実装は以下のように行いました。

log_and_diff.py

Import numpy as np

#産業用ロボット
df_machinary_order_data["産業用ロボット対数化"] = np.log10(df_machinary_order_data["産業用ロボット"]).diff()

階差を取った結果は以下のようになります。なお、階差を取ると最初の列(本記事のデータセットでは2005年4月)はNaNになるため、2005年5月からのデータセットにします。

df_oringinal.py

#2005年5月以降
months = month_lists[1:]
#対数&階差のデータセット df_original
df_oiriginal = df_oiriginal[months]

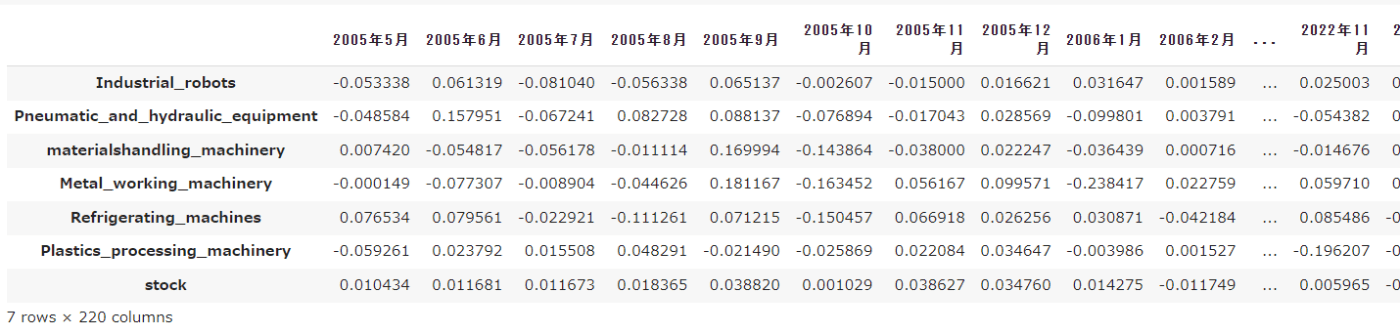
使用データフレーム
　続いて、iTransformerモデルを適用するためのデータを作成します。
iTransformerでは複数の時系列データ(variate tokens)に対して、各々過去データ(lookback length)を格納したデータを学習させます。ここで、時系列データを分割させて、バッチ(batch)としてまとめて学習させる方法を取ります。したがって、(batch,lookback,variates)の3次元のテンソル型配列を作成する必要があります。
　まず、(lookback,variates)の2次元配列を作成し、次元を拡張して(1, lookback,variates)の3次元の配列を作成します。以下は実装例です。本記事ではあるデータフレームの〇月～×月までの過去時系列データを抽出し、次元拡張して3次元にする方法を取りました。

Make_iTransformer_data.py

#iTransformer用のテンソル配列作成関数
def Make_iTransformer_data(df_csv,time_name,start_index,end_index,df_use) :
  #df_use : 時系列データをまとめる際に使用するデータフレーム
  #df_csv : 時刻をカラムに持つcsvのデータフレーム
  #start_index,end_index : 月のカラムの始まりと終わりのインデックス
  #time_name : 時刻カラム名(本記事では「時点」)
  #month : 取得月リスト
  months = list(df_csv[time_name][start_index:end_index])

  #iTransformerでは、3次元目の過去データ用のデータテンソル作成
  #(batch,lookbacknum,variates)
  #したがって、tensor.Size([1,lookbunnum,variates])のテンソル配列を作成
  #まず、tensor.Size([lookbunnum,variates])作成のための配列(np_target)を作成
  df_target = df_use[months].T
  np_target = df_target.to_numpy()

  #時系列データとして、tensor.Size([1,lookbunnum,variates])を作成
  #バッチをrepeatを用いて作成
  timeseries_data = torch.tensor(np_target)
  timeseries_data = timeseries_data.repeat(1, 1, 1)
  reslut_data = timeseries_data.to(torch.float32)

  # CPUまたはGPU上にテンソルを配置
  device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
  reslut_data = reslut_data.to(device)

  return reslut_data

この関数を使用した上で、torch.catを用いてバッチを増やしていきます。本記事では6個のバッチを作成し、1つのバッチに36時刻分の時系列データを格納しました。本記事では、2005年5月～2023年6月までの月次データ(データ数 218)を学習データとして、2023年7月と2023年8月の2ヶ月分の予測をします。詳細は、数値実験の節で説明します。

train_data.py

import torch

#訓練データ size (6,36,7)
train1_data = Make_iTransformer_data(df_machinary_order_data,"時点",1,37,df_oiriginal)
train2_data = Make_iTransformer_data(df_machinary_order_data,"時点",37,73,df_oiriginal)
train3_data = Make_iTransformer_data(df_machinary_order_data,"時点",73,109,df_oiriginal)
train4_data = Make_iTransformer_data(df_machinary_order_data,"時点",109,145,df_oiriginal)
train5_data = Make_iTransformer_data(df_machinary_order_data,"時点",145,181,df_oiriginal)
train6_data = Make_iTransformer_data(df_machinary_order_data,"時点",181,217,df_oiriginal)
# テンソルを結合して新しい形状を持つテンソルを作成
train_data = torch.cat((train1_data, train2_data,train3_data,
                        train4_data,train5_data,train6_data), dim=0)

iTransformerモデル実装と最適パラメータ探索

まず、iTransformerをインストールします。

!pip install iTransformer

iTransformerモデルは以下のように実装できます。GitHubによると、以下のようにモデルの実装、および、予測が可能です(2023/10/31時点)

iTransformer_sample.py

from iTransformer import iTransformer

# using solar energy settings

model = iTransformer(
    num_variates = 137,                 #時系列データ数
    lookback_len = 96,                  #時系列データの長さ
    dim = 256,                          # 埋め込みベクトルの次元数
    depth = 6,                          # 層の深さ
    heads = 8,                          # self attentionのhead数
    dim_head = 64,                      # headの次元数
    pred_length = (12, 24, 36, 48),     # 予測期間の長さ
    num_tokens_per_variate = 1,         # 時系列データに対して特徴量を増加する際に使用する変数。埋め込みベクトル×num_tokens_per_variateに拡張
)

time_series = torch.randn(2, 96, 137)  # (バッチ,時系列のデータの長さ, 時系列データの長さ)

preds = model(time_series)

# preds -> Dict[int, Tensor[batch, pred_length, variate]]
#       -> (12: (2, 12, 137), 24: (2, 24, 137), 36: (2, 36, 137), 48: (2, 48, 137))

上記のようにパラメータ設定ができるため、参考記事4のように最適パラメータ探索をしていきます。本記事の学習と検証に使う期間は、2005年5月～2023年6月(データ数 218個)とし、最適パラメータを求めた後、そのパラメータを使用して、2023年7月と2023年8月の2ヶ月の期間の予測をしていきました。また、各予測時刻の誤差の平均を最小化するパラメータを求めるようにし、1回の探索は、1800回の探索か610秒に学習時間が達するかのどちらかを満たすこととし、2400秒を超えたら全体の探索を終了し、誤差が最も小さいパラメータを選択しました。ここで、誤差とは、予測したデータである階差値を加算させ、対数変換のデータに戻したデータと、実際の対数変換のデータの誤差になります。そして、求めたパラメータに対し、2023年7月と2023年8月の2ヶ月の期間の予測をしていき、階差データの予測値を算出しました。この操作を3回実施し、予測の対数値の平均を算出します。以上をフローに、まとめると以下のようになります。
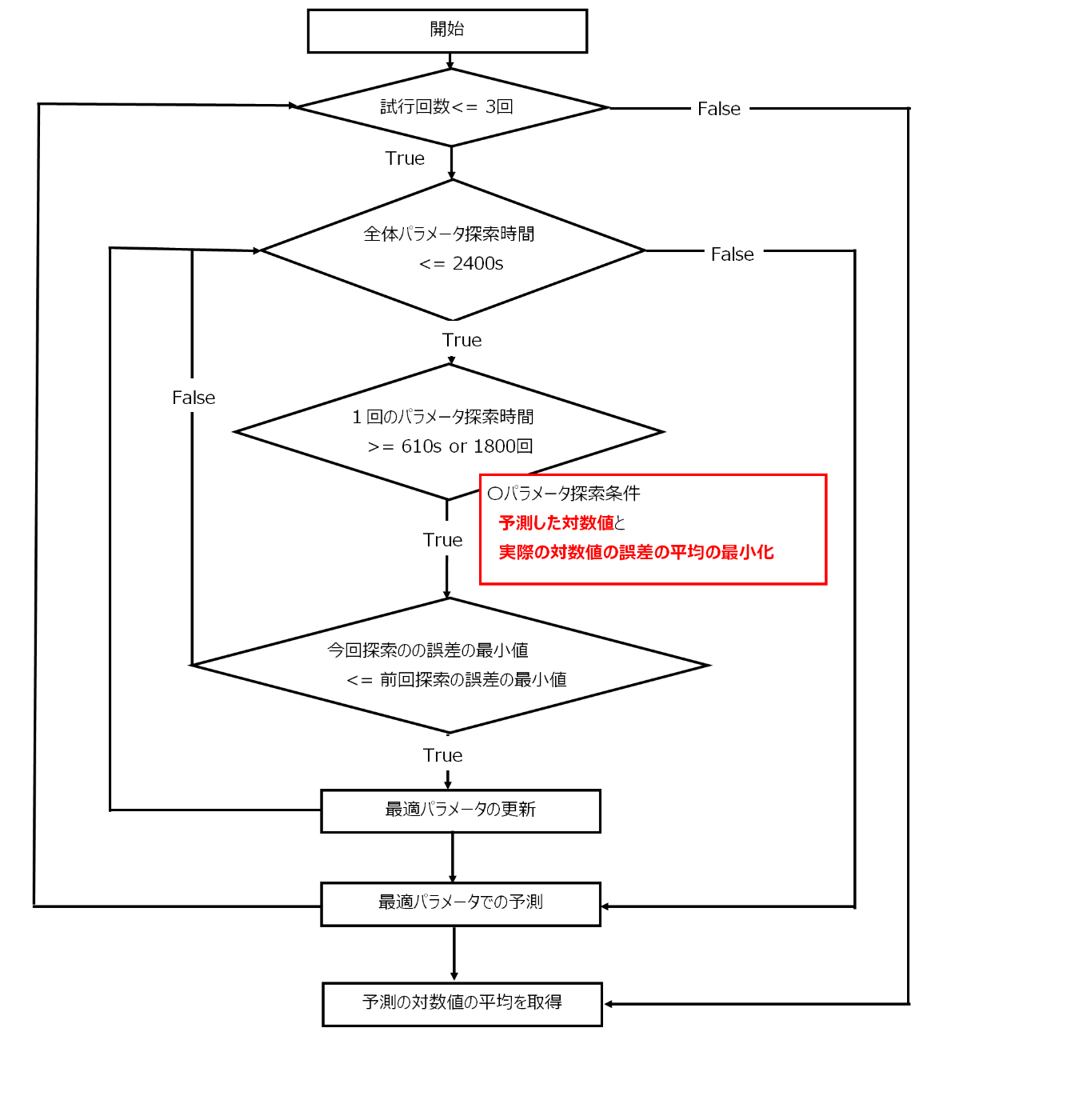
最適化手順
本記事ではoptunaを用いて最適パラメータ探索をしました。まず、1回分の探索部分(1800回の探索か610秒の探索時間の条件設定部分)の実装は以下のように行いました。なお、予測の階差から予測の対数値に戻すMake_dfdiff_reverse関数は説明の都合上後で説明します。

optuna_parameter.py

import optuna

#パラメータの最適値探索
def optuna_parameter(train,df_ori,valid_terms) :
    study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
    #探索回数 1800回 or 探索時間610秒に達するいずれかを満たせば、1回の探索終了
    study.optimize(iTransformer_params(train,df_ori,valid_terms), n_trials=1800,timeout=610)
    optuna_best_params = study.best_params

    return study

ここで、全体の探索関数にあたるiTransformer_paramsの関数は、以下のように実装しました。

iTransformer_params.py

#パラメータ探索関数
def iTransformer_params(train,df_ori,valid_terms) :
    
    def objective(trial) :
        #パラメータ設定
        params = {
            'num_variates' : 7,
            'lookback_len' : 36,
            'dim' :  trial.suggest_int('dim',250,350),
            'depth' : trial.suggest_int('depth',1,20),
            'heads' : trial.suggest_int('heads',1,20),
            'dim_head' : trial.suggest_int('dim_head',8,32),
            'pred_length' : 2,
            'num_tokens_per_variate' : trial.suggest_int('num_tokens_per_variate',2,25)
            #'num_tokens_per_variate' : 1
        }

        #パラメータ適用モデル
        itrans_model = iTransformer(
            num_variates = params['num_variates'],
            lookback_len = params['lookback_len'],
            dim = params['dim'],
            depth = params['depth'],
            heads = params['heads'],
            dim_head = params['dim_head'],
            pred_length = params['pred_length'],
            num_tokens_per_variate = params['num_tokens_per_variate']
        )

        #モデル予測
        itrans_preds = itrans_model(train)
        #結果の予測配列をテンソル型にする
        for key,value in itrans_preds.items() :
            pred_tensor = torch.tensor(value)
        pred_MAEtensor = pred_tensor.transpose(1, 2)
        #batch_count : バッチ数, graph_count : 時系列のデータ数, pred_step_count : 予測期間の長さ
        batch_count,graph_count,pred_step_count = pred_MAEtensor.shape

        #予測期間と実際の値の誤差
        index_lists = df_ori.index
        month_lists = df_ori.columns
        sumABS = 0.0

        for b in range(0,batch_count) :
          pred_arr = pred_MAEtensor[b].numpy() #予測値(階差)のデータ格納
          #df_result : 予測値を格納するデータフレーム
          start_months_index, end_months_index= valid_terms[b]
          result_months = month_lists[start_months_index+1:end_months_index]
          df_result = pd.DataFrame(data=pred_arr, index=index_lists,columns=result_months)
          #検証とテストのデータフレームを格納
          #df_valid : 実際の対数変換のデータフレーム
          #df_test : 階差の予測値を使用し、
          #          Make_dfdiff_reverse関数で算出した対数変換のテスト用データフレーム
          valid_months = month_lists[start_months_index:end_months_index]
          df_valid = df_ori[valid_months]
          df_test = Make_dfdiff_reverse(df_valid,df_result)

          for g in range(0,graph_count) :
            for ps in range(0,pred_step_count) :
              #実際の対数値と予測の対数値の誤差の計算
              sumABS += np.abs(df_valid.iloc[g,ps+1] - df_test.iloc[g,ps])

        return sumABS / (batch_count * graph_count * pred_step_count)

    return objective

実際には上の2つの関数(iTransformer_params.py と optuna_parameter.py)を用いながら、全体の探索時間2400秒が過ぎるまでパラメータ探索を行いました。実装は以下のように行いました。

search_params.py

optuna_count = 9　# 回数制限も書いておきました。別途調整してください。
best_values = 99999999
#best_params = ""
start_time = time.time()
for i in range(0,optuna_count):
  study = optuna_parameter(train_data,df_log,valid_terms)
  now_deal_time = time.time() - start_time
  if study.best_value < best_values :
    best_params = study.best_params
    best_values = study.best_value
  print("--------------------------------")
  print("optimize count", str(i + 1))
  print("best_params : ",best_params)
  print("best_values : ", best_values)
  print("--------------------------------")

  if 2400 <= now_deal_time :
    print("--------------------------------")
    print("optimize count", str(i + 1))
    print("best_params : ",best_params)
    print("best_values : ", best_values)
    print("--------------------------------")
    break

このようにして求めた最適パラメータに対して予測値を出力していきました。モデルの定義は以下の通りです。

iTransformer_bestparams.py

#モデル実装
itrans_model = iTransformer(
    num_variates = 7,
    lookback_len = 36,
    dim = best_params['dim'],
    depth = best_params['depth'],
    heads = best_params['heads'],
    dim_head = best_params['dim_head'],
    num_tokens_per_variate = best_params['num_tokens_per_variate'],
    pred_length = 2
    )
#モデル適用
itrans_preds = itrans_model(pred_train_data)
#予測値格納
for key,value in itrans_preds.items() :
  pred_MAEtensor = torch.tensor(value)

以上がパラメータ探索部分とそのパラメータを使用した予測値の出力部分です。次の節で値を代入して結果を示していきます。

数値実験と考察

前述の節でも簡単に述べましたが、本記事におけるデータを再度まとめます。
データセットの整理
　　iTransformerの学習データは、データの前処理の節のtrain_data.py部分で説明した通り、1つのバッチに36時刻分の時刻分の時系列データを格納した6つのバッチを作成し学習させます。モデルでは各バッチごとにpred_lengthの指定期間分(本記事の場合2ヶ月分)の予測を行っています。バッチごとの学習期間・予測期間をまとめると以下のようになります。
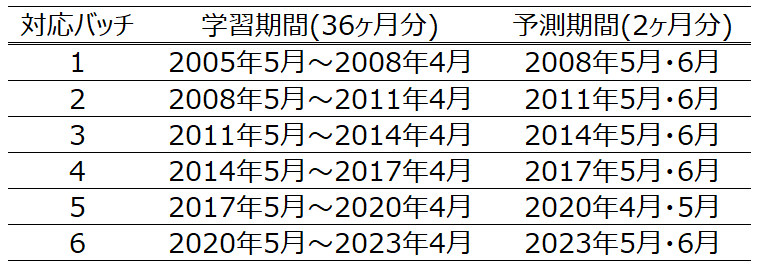
各バッチの学習期間と予測期間
上の表のようにバッチの学習期間と予測期間を重ねてバッチを作成しデータ数を可能な限り少なくできるようにしました。また本記事では、対数を取った後に階差を取って定常にした時系列を学習させています。そこで、最適パラメータ探索時の誤差測定時の対数値の比較では、予測の階差を使用して予測の対数値に戻す必要があります。本記事では、その動作をMake_dfdiff_reverse関数で行い、以下のように実装しました、

Make_dfdiff_reverse.py

#予測の階差を用いた実際の対数値のフレームの更新
def Make_dfdiff_reverse(df_ori,df_diff) :
  #結果データフレームの作成のための変数作成
  rows,columns = df_ori.shape
  df_result = df_ori.copy()

  for i in range(0,rows) :
    #前月の対数値の保存
    before_term = df_ori.iloc[i,0]
    for j in range(1,columns) :
      #前月の対数値に予測の階差値を加算して予測の対数値を作成
      df_result.iloc[i,j] = before_term + df_diff.iloc[i,j-1]
      #前月の対数値の更新
      before_term = df_result.iloc[i,j]

  return df_result

Make_dfdiff_reverseで使用している対数値と階差値の関係性は以下のようになります。
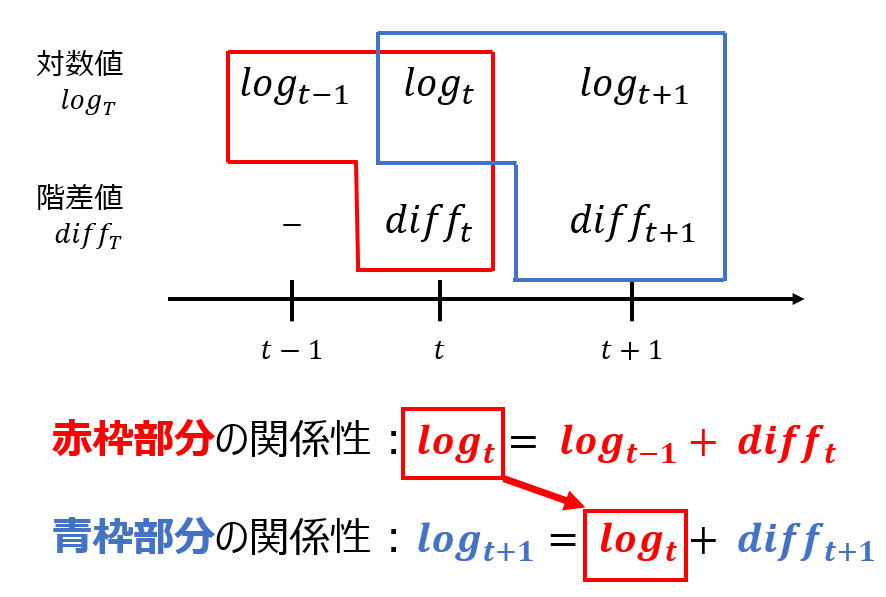
対数値と予測値の関係性
　したがって、予測期間のデータを検証するための実際の対数値の期間は、最初の階差を加算するために、前月分のデータも必要になり、予測期間2ヶ月 + 前月1か月分の3か月分必要になります。その期間をvalid_termmsとして以下のように設定しました。

valid_terms.py

valid_terms = [
    [36,39],    #2008年4月～6月
    [72,75],    #2011年4月～6月
    [108,111],  #2014年4月～7月
    [144,147],  #2017年4月～6月
    [180,183],  #2020年4月～6月
    [216,219]   #2023年4月～6月
]

この予測期間と、データの前処理の節のtrain_dataを用いて、iTransformerで最適パラメータを求めます。この結果に対して、iTransformerモデル実装と最適パラメータ探索の節のiTransformer_bestparams.pyを用いて、予測値を求めます。このとき使用する2023年7月と8月の予測値を取得するためのpred_train_dataを以下のように設定しました。

pred_train_data.py

#予測時使用データ
train1_data = Make_iTransformer_data(df_machinary_order_data,"時点",3,39,df_oiriginal)
train2_data = Make_iTransformer_data(df_machinary_order_data,"時点",39,75,df_oiriginal)
train3_data = Make_iTransformer_data(df_machinary_order_data,"時点",75,111,df_oiriginal)
train4_data = Make_iTransformer_data(df_machinary_order_data,"時点",111,147,df_oiriginal)
train5_data = Make_iTransformer_data(df_machinary_order_data,"時点",147,183,df_oiriginal)
train6_data = Make_iTransformer_data(df_machinary_order_data,"時点",183,219,df_oiriginal)
# テンソルを結合して新しい形状を持つテンソルを作成
pred_train_data = torch.cat((train1_data, train2_data,train3_data,train4_data,train5_data,train6_data), dim=0)

ここで、2023年7月と8月の予測値は、5つ目のバッチの予測値と考えられるので、iTransformerのモデルを適用したテンソル配列を、pred_tensorとすると、

pred_finalbatch.py

print(pred_tensor[5])

とすることが可能です。この作業を最適パラメータに対して実施し、予測の階差からMake_dfdiff_reverse.pyで予測の対数値を算出しました。これを3回行い、2023年7月と8月の受注金額に対する、予測の対数値の平均と実際の対数値と比較しました。
　実際の結果は以下のようになりました。まず、実際の対数値は以下の通りです。
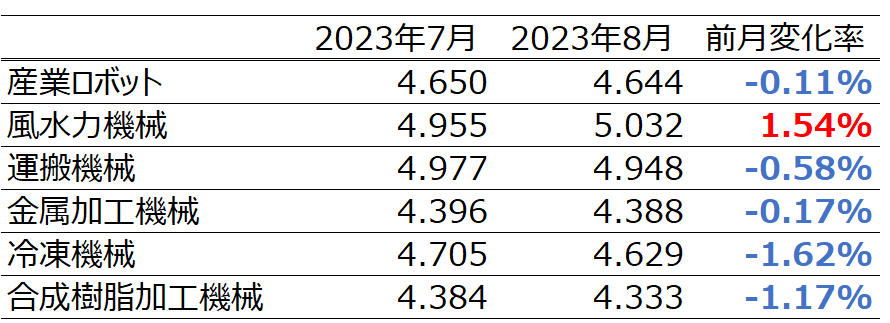
実際の受注金額の対数値
次に予測の対数値の平均は以下のようになりました。
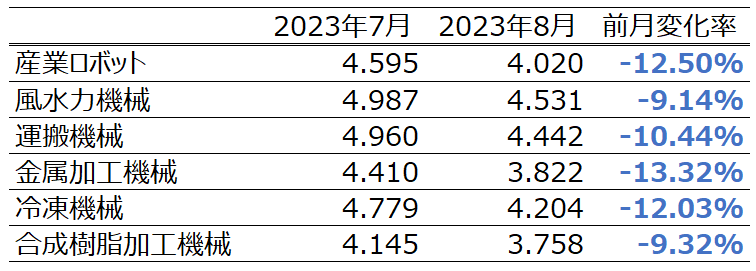
予測の受注金額の対数値
表を比較すると、2023年7月分に関しては良い精度で出力できていると考えています。しかしながら、実際値では、増加や減少が項目毎に存在する一方、予測値は、差はありますが全てのデータで減少しており、かつ、減少の幅が実際値より大きくなっていることが分かります。
　これは学習の中でデータに対して負の相関を学んでしまったことに加え、減少傾向を強く学習してしまった可能性があります。しかし可能性の話であり、実際はどのように学んだかを可視化できておりません。実際に予測値を使用する際は、意思決定をするのが人である以上、誤差が小さいからのみの理由では判断できないことが多いと考えています。そのような中で、過去のデータと予測値がどのような関係性があるのかという見方の1つとして、相関を色付けして示すヒートマップのようなデータを可視化することが一つの解決策だと考えているので、そこが今後の課題だと考えています。
ヒートマップ実装例
　一方、対数をべき乗計算して受注金額に戻した結果は以下のようになります。
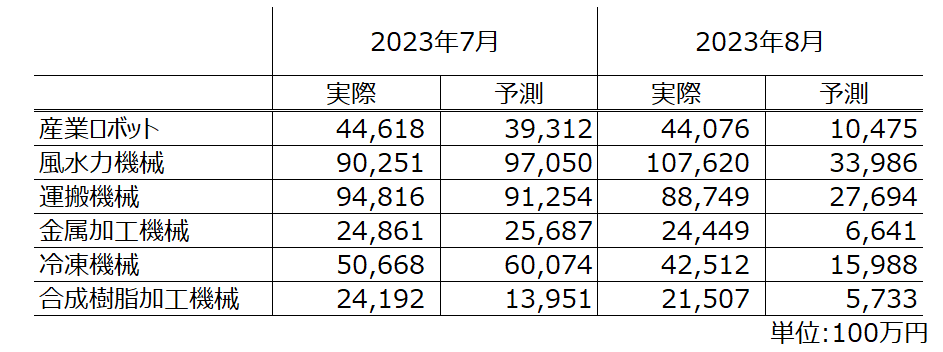
実際の受注金額との比較
金額ベースに戻すとより明確に8月の金額差が把握できます。これに関しては、私のモデル理解がまだ足らない点もあると思いますが、論文の時系列の項目数と比較すると圧倒的に足らないことが1つの要因であることは推測できます(論文だと137工場分の電力等を使用しています)。またバッチ処理でまとめて考えるため、各項目のデータ数も必要になり、220個分のデータでは少ない可能性もあります。私の論文理解も含めて、その点の見直しも必要だと考えています。
　この実装にあたり一番時間がかかった面は、最適バッチ数の探索と学習時系列の選定になります。
　最適バッチ数は各項目のデータ数の最適値が96というように読み取れたので、最初220のデータに対して96のデータ数でバッチを2つ作成し学習させたのですが、誤差が大きく断念しました。その後、その半分の48、24、、とやっていき、１バッチ36のデータ数で6つのバッチで最適であることが分かりました。このようにデータ数やおそらくデータの傾向も関連しているので、その点を考慮した最適なバッチ数の探索も今後の課題になります。
　また、学習時系列に対して明らかに類似性や相関のないデータを盛り込むと予測精度が下がることが分かりました。類似の時系列や相関のあるデータかどうかが分かれば、それらのデータを類似の系列として、iTransformerのモデルで学習させることが可能となり、精度向上が見込めると考えています。また類似性があるため、最適なバッチ数(1バッチのデータ数)を決定する際も、一定の目星をつけることができ探索時間を削減可能ではないかと考えています。
　この改善として、時系列クラスタリングを用いて、学習データを選定・まとめた後にモデルを適用することが時間・精度双方にとって良い手法であると考えています。今後はそのような実装をしていきたいです。

本記事のまとめ

本記事では、データ数が少ない項目に対して、複数の項目に対して相関に考えることができれば、少ないデータ数でも分析・予測が可能ではないかという動機に基づき、少ないデータ数での予測に焦点をあてて述べていきました。今回は自然言語処理で発展しているTransfotmerの改善モデルであるiTransformerを用いて2ヶ月分の受注金額予測を行った結果、1か月目については一定の精度がありました。複数月の予測という観点では、論文理解不足もあると思いますが、論文と比較して、学習させる項目数の少なさや各項目のデータ数の少なさも考えられるので、項目の数の多いデータで再実験をしたいです。その他の課題としては、ヒートマップなど描画による予測結果と時系列データの関係性の可視化や、時系列クラスタリングを用いた学習データの選定やバッチ数の特定によるデータの前処理時間の削減・精度向上などが挙げられます。

参考文献

〇学習データセット

〇Transfomer以外の時系列解析の参考文献

〇Transformerの参考文献

〇iTransformerの参考文献

〇その他の参考論文

Discussion

iTransformerの詳しい説明＆実装例の提示ありがとうございます．
論文をみていざ使って見ようにも実装やその活用方法が乏しくて困っていたところ
大変ありがたいです．
順に実行しているのですがsearch_params.pyの
for i in range(0,optuna_count):
study = optuna_parameter(train_data,df_log,valid_terms)
df_logがどういったデータなのかわからず困っています．
できましたらおしえていただけるとありがたいです．

S.A

コメントありがとうございます。

またご指摘ありがとうございます。
初めに1点だけ謝罪させてください。

私情で申し訳ありませんが、ここ数ヶ月中に記事関連のコーディングデータがほとんど消えてしまっていました。

その中でコードを書いたのがだいぶ昔で、私自身もきちんと追える点と追えない点があります。
その上でなのですが、

「df_log」は、iTransformer_params.py内の誤差計算で使用する

予測データである「df_result」と検証用の実際のデータフレームである「df_valid」のうち、

「df_valid」の参照データフレームである『df_ori』に対応しています。
以上のことから、

訓練データとして対数変換したdf_machinary_order_dataをがコーディング中にdf_logになっていると考えています。
私個人の記事であるのに関わらず、こちらの都合で曖昧な回答になってしまい申し訳ございません。

私も確認し終えたら記事含めて修正します。

回答ありがとうございます。消えてしまったのは残念ですね。
iTransformerの日本語での実験例はこの記事だけだとおもうので
復旧するといいですね！
ご指摘に従って変更してみたのですが、何かが間違っているようで
optunaの部分で試行錯誤しています。この記事を書かれたS.A様の
技量に感心する次第です。

S.A

確認ありがとうございます!
私の方でも確認してみます。