Pythonによる時系列クラスタリング(Euclid/DTW,k-shape,PCA/t-SNE)の実装と評価
前回記事までのまとめ、および、本記事の目的
多品種少量生産下における需要予測手法の確立に向けて、前回記事までは、まず、SARIMA、LSTM、NeuralProphetの3つの時系列解析手法の実装の評価を実施し、Store Item Demand Forecasting Challengeのデータセットにおいて、product 1における2017年の需要予測を実施し、NeuralProphetが良いという結果を得ました。
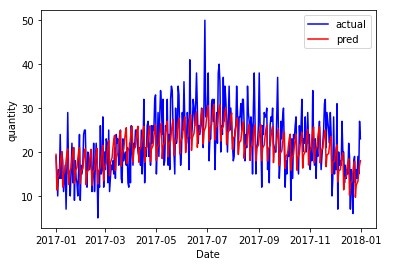
次に上記の結果を利用し、予測時間をかけず精度の良い予測をするための手法の考察をしました。その結果、変動要因に類似性がある場合、変動要因の除去を除いた定常性のある時系列データに対して類似性のある品番毎にまとめた上で、各グループにおける基準品種のパラメータを利用することにより、予測時間をかけずに可能な限り良い精度が得られるのではないかと考えました。
そこで、今回は、時系列データを類似性のある品種毎にまとめる方法として、時系列クラスタリングの手法を用いて類似品番をまとめる方法を考えていきます。今回は、Euclidean Distance、DTW、kshape、PCAとt-SNEによる次元削減を利用したクラスタリングをしていきます。その後、精度の評価としてSSEによる評価、および、クラスタリング結果に基づく需要予測による評価を実施します。最後に、これらの結果を通して実際の実装手順を考えていきます。
機械学習の分類
通常のプログラミングはあるデータに対して、ルールを決めてそのルールに応じた答えを出力するもので、このルール部分をコーディングしていきます。一方機械学習は、ルールをコーディングしていくものではなく、データから有益な情報や構造を抽出し、ルールを発見していく手法になります。データから有益な情報や構造を抽出するにあたり、機械学習は教師あり学習・教師なし学習・強化学習という方法を使います。
教師あり学習は、データに対して正解となるラベルがついたデータを学習する手法で、特徴量と正解ラベルがセットになっており、その関係性を学習しルールを導出します。時刻に沿って需要のデータが存在し、その関係性を分析して将来の需要を予測する時系列解析もその1種です。
教師なし学習は、正解ラベルを与えず、各データの規則性などを導出する手法で、各データの特徴量を変換し異なる形式で表現したり、データを一定の集合にまとまりに分類していきます。「各データの特徴量を変換し異なる形式で表現」する手法としては、より少ないと特徴量でデータを分析するための次元削減が挙げられ、「データを一定の集合にまとまりに分類」する手法としては、クラスタリングという手法が挙げられます。
強化学習は、試行錯誤を繰り返しながら、価値が最大化されるように学習する手法になります。今回は詳しく説明しませんが、個人的に興味があるので勉強したら何かしらの記事にしたいです。
さて、本記事の第一目標は、時系列データを類似性のある品番毎にまとめることであるので、教師なし学習におけるクラスタリングの手法の説明と実装を行い、理解を深めることができればと考えています。
時系列クラスタリング
時系列クラスタリング手法として、サーベイ論文がまとめられています。(参考文献①、参考文献②)。
時系列クラスタリングの手法は、参考文献の内容を引用すると以下のようにまとめられます。
・形状ベースアプローチ
時系列データの形状の特徴に着目してクラスタリングを実施
・特徴ベースアプローチ
低次元のベクトルに変換後、クラスタリングを実施
・モデルベースアプローチ
クラスターごとにモデルを仮定し適合させることでクラスタリングを実施
前節で説明をした次元削減は、特徴ベースアプローチに該当すると考えられます。時系列クラスタリング次元削減ではPCAやt-SNEが簡単に実装できます。また、同一系列上の類似度を距離で測るEuclidean Distance、DTWも該当すると考えられます。形状ベースアプローチには、時系列データである波形の特徴の類似性を測定しようとするkshapeなどが該当すると考えられます。
それでは実際に時系列クラスタリングをしていき、類似品種をクラスタリングする方法について考えていきます。
時系列クラスタリングの実装
機械学習における適用手順に対して時系列クラスタリングの手順をあてはめていくと、下記のようになります。
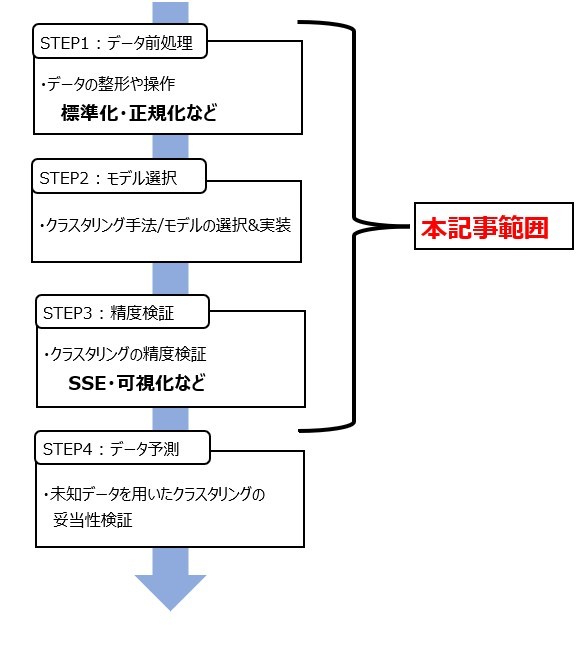
時系列データではスケールの違うデータも多くそのままクラスタリングを実施すると、本当は類似性があるデータであってもスケールの違いから、類似性がないと判断してしまうことになります。したがって、時系列クラスタリングではデータの前処理において標準化や正規化をすることで、各データのスケールを合わせることが特に重要になります。標準化・正規化した後は、適切なクラスタリング手法を選定・実装を行い、精度評価をしていきます。精度評価の方法は、SSEによる評価、および、クラスタリングした類似製品の需要予測結果の評価の2つの方法を実施します。
まずデータの前処理をします。本記事では標準化を選択しました。
from sklearn.preprocessing import StandardScaler
#標準化
scaler_std = StandardScaler()
#df_clustering : クラスタリングを実施するデータフレーム
df_clustering.loc[:,:] = scaler_std.fit_transform(df_clustering)
データの標準化ができたので実際に時系列クラスタリングの実装をしていきます。
Euclid Distance/DTW
時系列データなどの波関数の類似度を計算する際には、ユークリッド距離やDTWを用いることが可能です。ユークリッド距離での測定は、系列の長さが同一である必要がありますが、計算速度が速いです。一方、DTWはDynamic Time Warpingの略で、日本語では動的時間短縮法と呼ばれる手法です。DTWは動的計画法を用いて、2つの時系列の間の距離同士が最短となるパスを総当たりで求める手法です。このような性質上、選択済みの時点も選択可能なため、時系列同士の長さや周期がずれていても類似度を算出することができます。
上記2つはtslearnライブラリのTimeSeriesKmeansを用いた上で、metricのパラメータを変更することで簡単に実装できます。
まずtelearnをインストールします。
!pip install tslearn
実装は以下の通りです。
from tslearn.clustering import TimeSeriesKMeans
import collections
#metric : ユークリッド距離(euclidean) , DTW(dtw)
metric = 'euclidean'
# cluster数
n_clusters = 3
#クラスタリングの実装
tskm_base = TimeSeriesKMeans(n_clusters=n_clusters, metric=metric,
max_iter=100, random_state=42)
tskm_base.fit(df_clustering.T.values)
#クラスタリングごとの表示
cnt = collections.Counter(tskm_base.labels_)
clusters = list(tskm_base.labels_)
cluster_labels = {}
for k in cnt:
cluster_labels['cluster-{}'.format(k)] = cnt[k]
# クラスターごとの数
print(sorted(cluster_labels.items()))
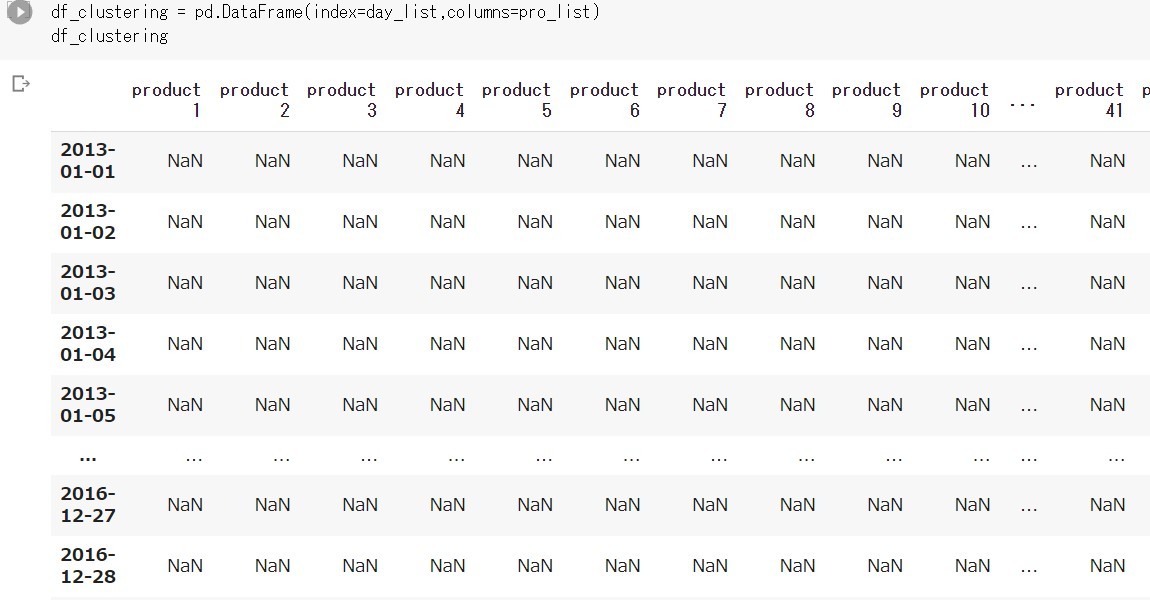
なお、クラスタリングに使うデータフレームdf_clusteringは、インデックスに日付、カラムに品種を設定したものとなります。
k-shape
k-shpeという手法は、2005年に提唱された方法(参考論文)です。この手法は、時系列データを波形の関数と考え、波形の特徴である位相と振幅に着目した距離尺度を用いて類似性を判断しようとする手法になります。この論文はきちんと読んで解説記事のようなものを挙げる予定ですが、簡単に考え方のポイントがこのサイトにまとめられているので今回はそちらを参考にして下さい。Kshapeもtslearnライブラリで実装できます。
from tslearn.clustering import KShape
#metric : ユークリッド距離(euclidean) , DTW(dtw)
metric = 'euclidean'
# cluster数
n_clusters = 3
#クラスタリングの実装
ks = KShape(n_clusters=n_clusters, random_state=42)
labels_ks = ks.fit_predict(df_clustering_TSNE)
#クラスタリングごとの表示
KS_cluster = list(labels_ks)
cnt = collections.Counter(KS_cluster)
cluster_labels_KS = {}
for k in cnt:
cluster_labels_KS['cluster-{}'.format(k)] = cnt[k]
# クラスターごとの数
print(sorted(cluster_labels_KS.items()))
PCA/t-SNE
続いて次元削除をした後、k-means法でクラスタリングする方法を考えていきます。次元削除の方法を説明する前に双方で扱うk-means法を説明していきます。
k-means法は各クラスタリングの集合の重心を更新していき、計算ステップの上限を満たすか、クラスタリングの変化がなくなるまで更新していく手法になります。図での詳細や簡単な説明動画は、このサイトやこの動画が分かりやすいと思うので参考にして頂ければと思います。
k-eams法の実装は以下のようになります。
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,# クラスターの個数
n_init=20,
max_iter=100,# k-meansアルゴリズムを繰り返す最大回数
random_state=42)
# fit_predictメソッドによりクラスタリングを行う
Y_km = km.fit_predict(cluster_PCA)
PCA_cluster = list(Y_km)
cluster_labels_PCA = {}
for k in cnt:
cluster_labels_PCA['cluster-{}'.format(k)] = cnt[k]
# クラスターごとの数
print(sorted(cluster_labels_PCA.items()))
PCA
PCAは、Principal Component Analysisの略で、日本語では主成分分析と呼ばれます。この手法は、多数の変数の中で最も効率よく説明できる変数を構築することで、データを圧縮する手法になります。つまり、高次元で表現されているデータを低次元で説明することに適した手法となり、次元削除の方法として様々な機械学習の分野において扱われています。アルゴリズムについては、このサイトが分かりやすいと思うので、参考にしてください。
PCAの実装は以下のように行い、上のKmeans.pyと組み合わせてクラスタリングを実施していきます。なお、PCAとt-SNEでの次元削減時に使用するデータフレームは、Euclid DistanceやDTWで作ったデータフレームとインデックスとカラムが逆になります。
from sklearn.decomposition import PCA
#データフレームを逆にする
df_clustering_TSNE = df_clustering.transpose()
#PCAによる次元削除
n_components = 2 #今回は”2”
cluster_PCA = PCA(n_components=n_components, random_state=42).fit_transform(df_clustering_TSNE)
# fit_predictメソッドによりクラスタリングを行う
Y_km = km.fit_predict(cluster_PCA)
PCA_cluster = list(Y_km)
cluster_labels_PCA = {}
for k in cnt:
cluster_labels_PCA['cluster-{}'.format(k)] = cnt[k]
# クラスターごとの数
print(sorted(cluster_labels_PCA.items()))
t-SNE
t-SNE(t-Distributed Stochastic Neighbor Embedding)は、2008年に提案された手法(参考論文)です。この手法は、元のデータ同士の近さが可能な限り等しくなるように、高次元のデータを低次元に圧縮させた後、近傍点がどのくらいあるかを求めることでクラスタリングする手法となります。t-SNEの詳細は、このサイトやこの動画が分かりやすくまとめられています。なお、後でこの論文についても解説記事を挙げられればと思います。
from sklearn.manifold import TSNE
#データフレームを逆にする
df_clustering_TSNE = df_clustering.transpose()
#t-SNEによる次元削除
n_components = 2 #今回は”2”
cluster_tSNE = TSNE(n_components=n_components, random_state=42).fit_transform(df_clustering_TSNE)
# fit_predictメソッドによりクラスタリングを行う
Y_km = km.fit_predict(cluster_PCA)
PCA_cluster = list(Y_km)
# fit_predictメソッドによりクラスタリングを行う(Kmeans)
Y_km = km.fit_predict(cluster_tSNE)
TSNE_cluster_Kmeans = list(Y_km)
cnt = collections.Counter(TSNE_cluster_Kmeans)
cluster_labels_TSNE = {}
for k in cnt:
cluster_labels_TSNE['cluster-{}'.format(k)] = cnt[k]
# クラスターごとの数
print(sorted(cluster_labels_TSNE.items()))
クラスタリングの評価
前節では各クラスタリング手法の実装と簡単な説明をしました。ここでは、SSE(クラスター内誤差平方和)、および、クラスタリングに基づいた実際の需要との差としてMAEを用いて評価していきます。
SSEによる評価
SSEとは各クラスターの重心から各点までの距離の平方和になります。したがって、この値が小さいほど重心に近いデータをまとめていることになり、良いクラスタリングと言えます。k-means法で妥当なクラスター数を求める方法の1つにエルボー法があります。この手法は、クラスター数とSSEの関係性を可視化して、SSEの値が緩やかに減少し始める数を妥当なクラスター数と捉える手法です。ただこの手法は必ず滑らかに減少するとは限らず、クラスターを決定する理由が明確に定まっていないときやデータの知見が少ない時に使う等、あくまで参考値となっております。
distortions = []
# クラスター数1~10を一気に計算
for i in range(1, 11):
km = KMeans(n_clusters=i,
n_init=20,
max_iter=100,
random_state=42)
# クラスタリングを実行
km.fit(cluster_tSNE)
#print("Distortion: %.2f" % km.inertia_)
# SSE取得
distortions.append(km.inertia_)
# グラフのプロット
plt.plot(range(1, 11), distortions, marker="o")
plt.xticks(np.arange(1, 11, 1))
plt.xlabel("Number of clusters")
plt.ylabel("Distortion")
plt.show()
ではSSEの評価をしていきます。クラスタリングする際には、当然時系列データが必要なので、今回必要なデータを準備する必要があります。
今回扱う時系列データは、初回記事と同じデータであり類似性がある時系列データになります。
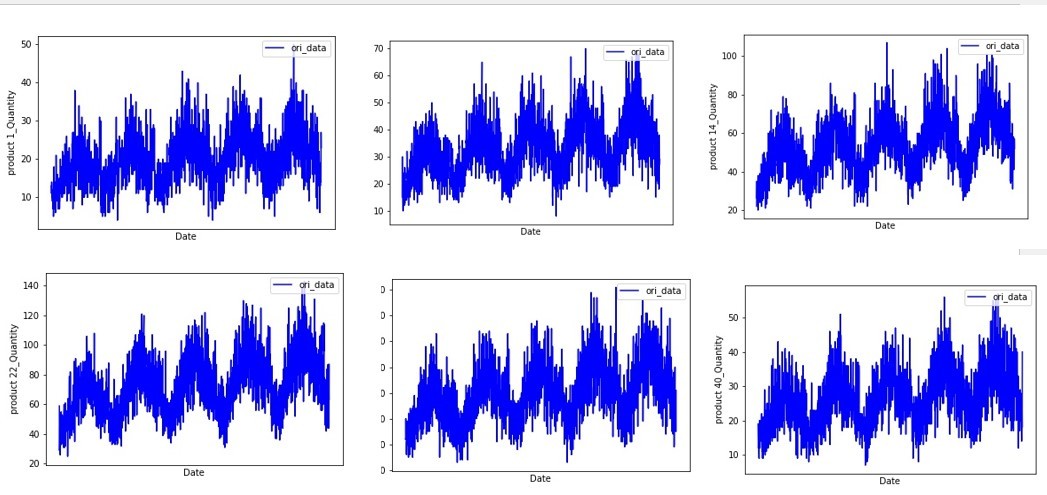
前回記事より、類似性の高い需要予測では、原系列から変動要因を除去し定常性がある時系列データに対して類似品種でクラスタリングをした上で、基準品種の結果を流用する方法を使えば、可能な限り予測時間を抑えつつ良い精度を保持できる手法を確立できると考えました。そこで、変動要因を除去した「誤差成分」の時系列データに対して、時系列クラスタリングを実施し、SSEによる評価や類似品種への需要予測の評価を通して、どのクラスタリング手法がよいのか、そして、どうすれば予測時間をかけずに予測結果の他品種への流用ができるかを考えていきます。今回の評価までの流れを簡単に図示します。
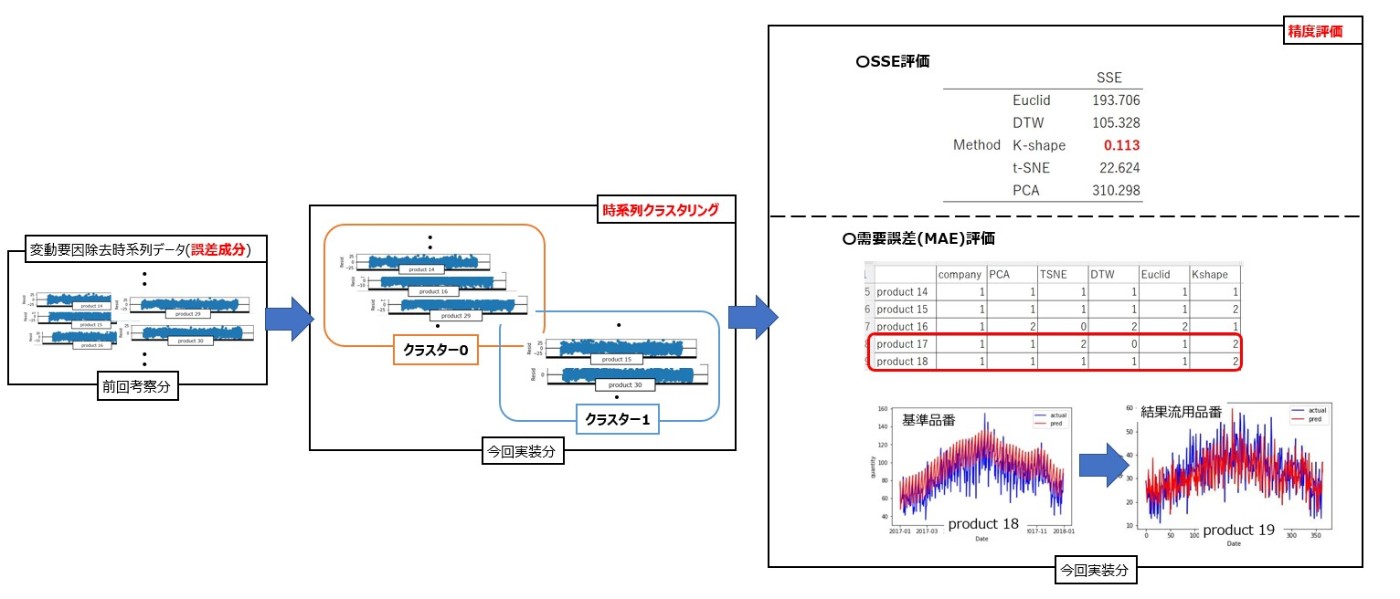
まず誤差成分を取り出していきます。誤差成分は以下のように抽出できます。
import statsmodels.api as sm
from statsmodels.tsa.seasonal import seasonal_decompose
#変動要因の除去
# res.target.resid.values : 誤差成分の値出力
res_target = sm.tsa.seasonal_decompose(df_res,period=period)
このように抽出したデータに対しStandardScale.pyのように標準化します。そして、時系列クラスタリングの実装の節を参考に、Euclid Distance/DTW、k-shape、PCA/t-SNEの次元削減によるクラスタリングを実施していきます。クラスタリング結果は以下の通りです。
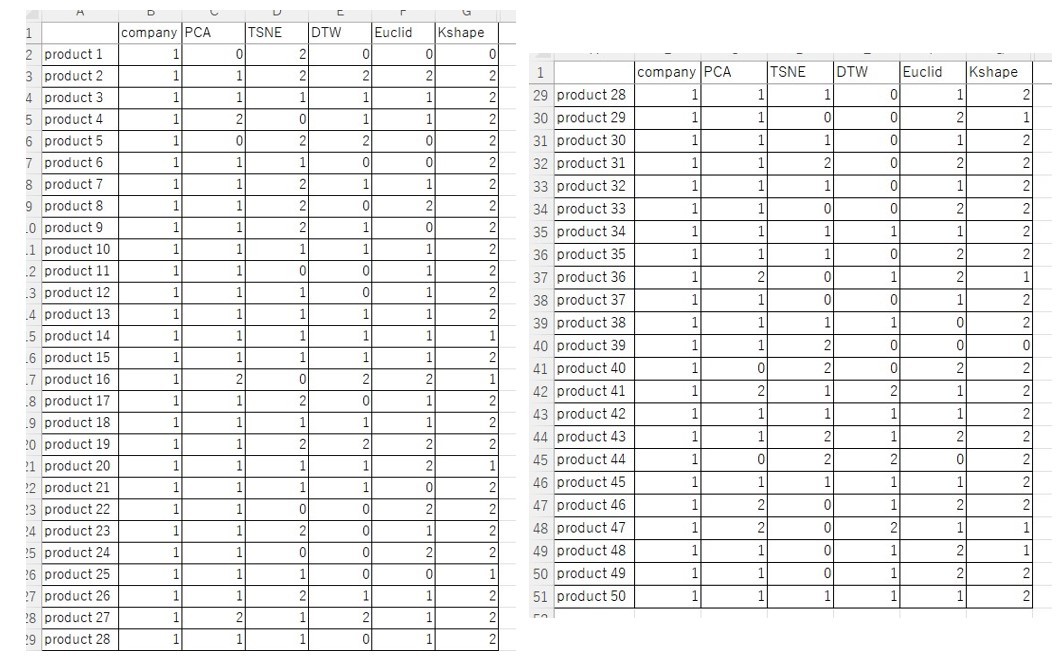
ではSSEの実装と評価をしていきます。SSEは、elnbow.pyで示した通り「km.inertia_」で簡単に出力可能です。まずエルボー法を例示していきます。本記事ではt-SNEの結果を挙げます。
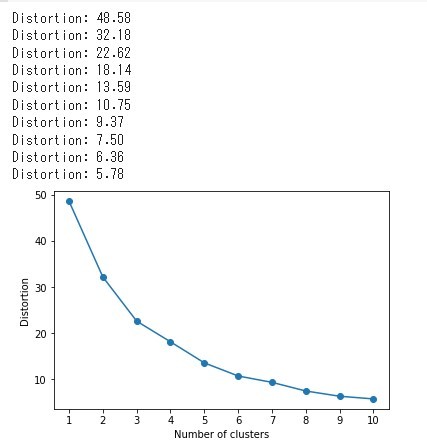
グラフを見ると大幅な減少をしているわけではありませんが、クラスター数が1~3までは約10の差がある一方、それ以降は半分の5で減少をしています。また、今回クラスターの数だけ時系列解析のディープラーニング(NeuralProphet)をしていくので、多すぎても時間がかかることも考え、クラスター数は「3」にします。
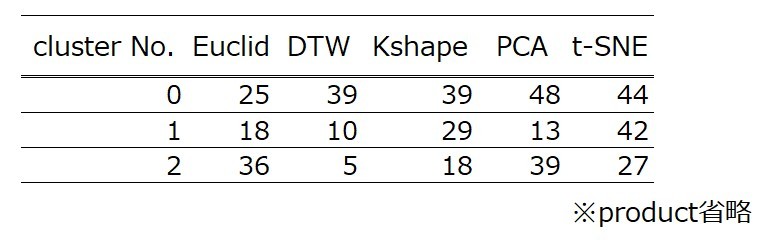
またPCA/t-SNEによる削除後の次元を「2」として、各手法のSSEの値を比較してみると以下のようになります。
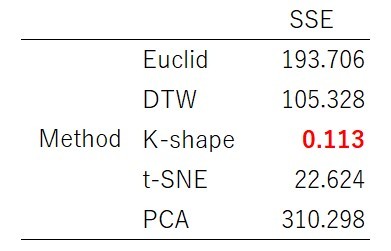
この結果からSSEでの観点で評価は、K-shapeが最も良いことが分かります。
需要予測による評価
次にこのクラスタリングに基づいた需要予測の精度を評価していきます。
前回記事では、最初に需要予測をしたproduct 1を基準品種に定め、NeuralProphetの需要予測結果を他品種への流用をしていきました。しかしながら、この決め方は時系列データの類似性が低い品種を選択してしまった場合、全体の予測精度が低くなってしまうのではないかと考え、各クラスターで基準品種を選びその結果の流用を試みます。クラスターは類似性のあるデータのまとまりであり、時系列データにおけるクラスターは、傾向の似ている時系列のまとまりです。その中でそのクラスターの傾向を上手く示せているのは、URLを見てわかるように各クラスター重心であるため、各クラスター内のデータにおいて最も重心に近い点、つまり、重心との距離が最も短いデータを基準品種とすることを考えました。
KMeansやTimeSeriesKMeansにはデータと各クラスターの重心との距離をn次元配列で返すtransformメソッドが容易されており、簡単に距離を知ることができます。最小の距離を取得する方法を例示します。
#クラスタリングデータフレームからの距離配列の格納
ks_transform = ks.fit_transform(df_clustering_TSNE)
#品種番号はproduct 1と「1」から始まるので最小の品種の要素数に +1 しています
cluster0_pro = np.argmin(ks_transform[:,0]).flatten()[0] + 1
cluster1_pro = np.argmin(ks_transform[:,1]).flatten()[0] + 1
cluster2_pro = np.argmin(ks_transform[:,2]).flatten()[0] + 1
print(cluster0_pro,cluster1_pro,cluster2_pro)
しかしながら、Kshapeにはtransformメソッドのようなものが用意されておらず、距離が測れなかったので、DTWを用いて重心との距離を測ることにしました。実装例を以下に示します。
from tslearn.metrics import dtw
#距離格納データフレーム df_distance
df_distance = pd.DataFrame(index=pro_list,columns=["Kshape_cluster","cluster0","cluster1","cluster2"])
df_distance["Kshape_cluster"] = list(labels_ks)
# kshapeアルゴリズムでクラスタリングする
n_clusters = 3
ks = KShape(n_clusters=n_clusters, random_state=42)
ks.fit(df_clustering_TSNE)
# 各クラスタに対して最も近いデータを抽出する
labels = ks.labels_ #ラベル
cluster_centers = ks.cluster_centers_ #重心
for i in range(len(df_clustering_TSNE)) :
#print("product " + str(i + 1))
#距離リストの作成
ori_data = df_clustering_TSNE.iloc[i,:].values
min_matrix = 0
for j in range(n_clusters):
#1年分の時系列データでのdtw
DTW = dtw(ori_data.reshape(-1,1), cluster_centers[j])
#DTWを格納
cluster_str = "cluster" + str(j)
#print(cluster_str,DTW)
df_distance[cluster_str][i] = DTW
#クラスター番号0の最小距離の測定
df_cluster0 = df_distance[["Kshape_cluster","cluster0"]].query("Kshape_cluster == 0")
print(df_cluster0.sort_values(by="cluster0").head(1))
実装結果である基準品番は以下の通りです。
では需要予測での評価をしていきます。まず基準品番での需要予測を実装します。実装の詳細は、初回記事や前回記事を参考にしてください。なお、今回は予測時間は15分で、パラメータの組み合わせを少なくするために、sesonality_regは変数に入れていません。なお再現性のプログラム作成のため、random_seedを設定しています。
from neuralprophet import NeuralProphet, set_random_seed
def BestparamsforNeuralProphet(pn,study) :
period = 365
path = '/content/params.txt'
# パラメータ設定
m = NeuralProphet(
changepoints_range = study.best_params['changepoints_range'],
n_changepoints = study.best_params['n_changepoints'],
trend_reg = study.best_params['trend_reg'],
yearly_seasonality = True,
weekly_seasonality = True,
daily_seasonality = False,
epochs = None,
batch_size = None)
#訓練データとテストデータ作成
querystr = 'product_name == "' + pn + '"'
df_target = df_company1.query(querystr)
df_target = df_target[["order_date","quantity"]]
df_target = df_target.query("order_date <= '2017-12-31'")
data = df_target.rename(columns={'order_date': 'ds', 'quantity' : 'y'})
train = data[data['ds'] <= '2016-12-31']
valid = data[(data['ds'] >= '2017-01-01')&(data['ds'] <= '2017-12-31')]
#学習
set_random_seed(42) #random_seed
metric = m.fit(train,freq="D")
future = m.make_future_dataframe(train, periods=period)
forecast = m.predict(future)
#予測
pred = forecast[['ds','yhat1']]
#MAE用配列
valid_y = valid['y'][-len(valid):]
forcast_y = pred['yhat1']
#最適パラメータとMAEのテキスト出力
s = pickle.dumps(study.best_params)
d = pickle.loads(s)
with open(path, mode='a') as f:
f.write("☆" + pn + " 最適パラメータ : " + str(d) + "\n")
f.write("☆" + pn + " MAE : " + str(mean_absolute_error(valid_y,forcast_y)) + "\n")
f.close()
optuma設定は以下の通りです。
def objective_variable(train,valid):
#パラメータ設定
def objective(trial):
params = {
'changepoints_range' : trial.suggest_discrete_uniform('changepoints_range',0.8,0.95,0.01),
'n_changepoints' : trial.suggest_int('n_changepoints',50,65),
'trend_reg' : trial.suggest_discrete_uniform('trend_reg',0,2,0.01),
}
#パラメータ適用によるモデル
m=NeuralProphet(
changepoints_range = params['changepoints_range'],
n_changepoints=params['n_changepoints'],
trend_reg = params['trend_reg'],
yearly_seasonality = True,
weekly_seasonality = True,
daily_seasonality = False,
epochs = None,
batch_size = None)
#モデル予測
set_random_seed(42)
metric = m.fit(train,freq="D")
future = m.make_future_dataframe(train,periods=len(valid))
forcast = m.predict(future)
#MAE
train_y = train['y'][-len(valid):]
forcast_y = forcast['yhat1']
MAE = mean_absolute_error(train_y,forcast_y)
return MAE
return objective
def optuna_parameter(train,valid):
study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
study.optimize(objective_variable(train,valid), timeout=900)
optuna_best_params = study.best_params
return study
これらを組み合わせて、基準品種の最適パラメータを取得していきます。なお、2023/03/16日時点で、pytoch-lightingのバージョンに対して現在のNeauralProphetの最新バージョン互換性がなくなったのか、pytoch-lightingの古いバージョンをインストール必要がでたみたいなので気を付けてください(参考url)。
!pip install install PyTorch-Lightning==1.8
上述の3つのコードで算出した基準品番の需要予測結果を流用し、他品番の需要予測を行っていきます。他品番への結果の流用方法は、前回記事の時系列データの平行移動の考え方を用います。これは変動要因が類似している時系列データは、基準品番の変動要因の時系列データに対して、y軸上に平行移動すれば各品種の系列データになるのではないかという考えで実装したものです。具体的な実装手順は、前回記事を参考にしてください。
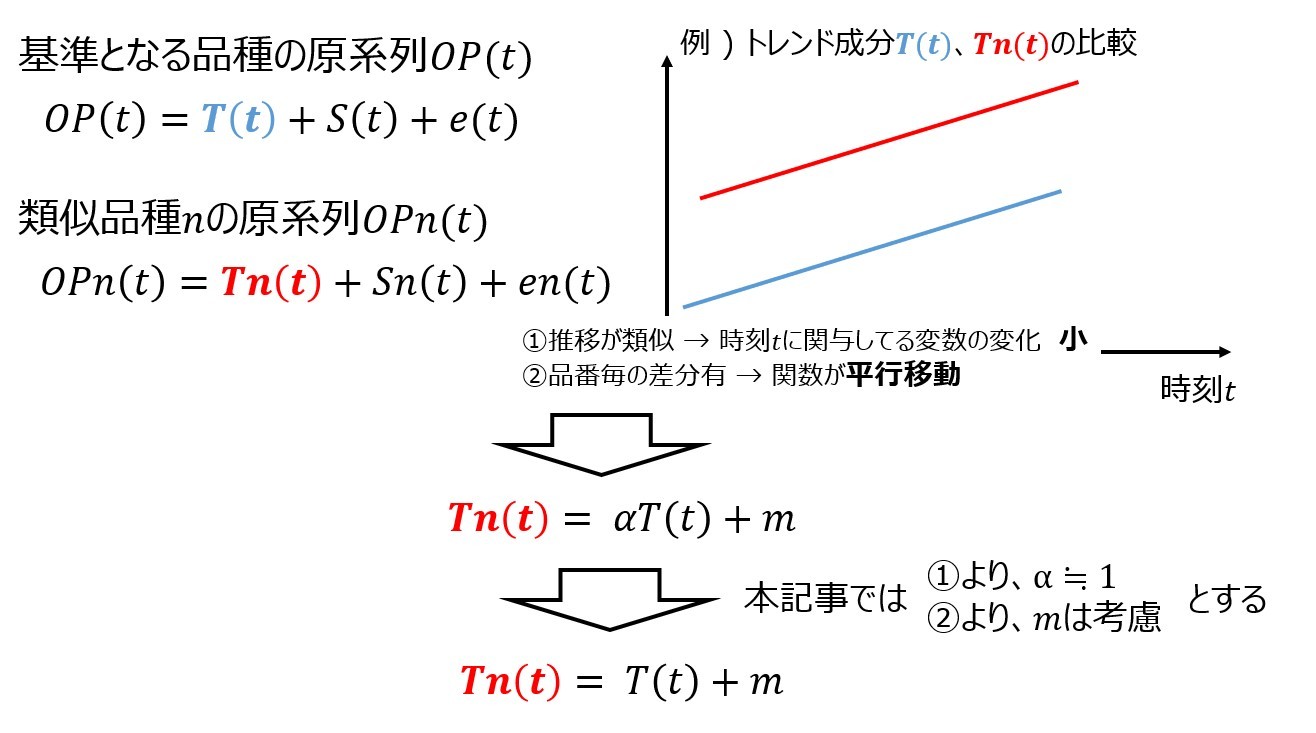
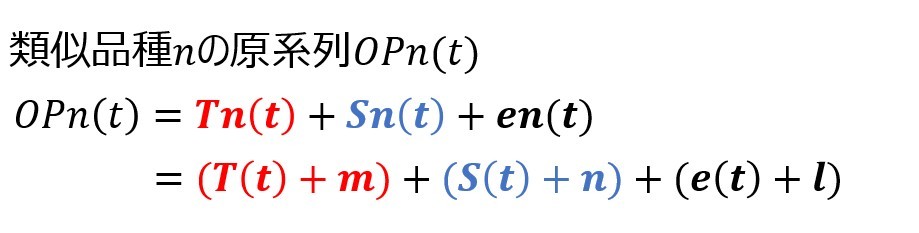
以下は実装例です。
def Translate_params(trend,season,resid,valid) :
def objective(trial) :
#最適パラメータ候補設定
params ={
"m" : trial.suggest_float('m',-30,70),
"n" : trial.suggest_float('n',-20,35),
"l" : trial.suggest_float('l',-20,35)
}
#平行移動分を考慮した予測値の算出
pred = (np.array(trend) + params['m'] +
np.array(season) + params['n'] +
np.array(resid) + params['l'])
#valid(2016年までの需要量との差分比較
MAE = mean_absolute_error(valid,pred)
return MAE
return objective
def optuna_Trans(trend,season,resid,valid):
study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
study.optimize(Translate_params(trend,season,resid,valid), n_trials=980)
optuna_best_params = study.best_params
return study
#変動要因格納データフレーム
df_pro_seasonal_decompose = pd.DataFrame(columns=["order_date","trend","seasonal","resid","quantity"])
#pn_listの最初の要素は基準品番にとして、for文を回しています。
for pn_index in range(0,len(pn_list)) :
if pn_index == 0 :
#基準品種のトレンド・周期・誤差の抽出
res_pred = seasonal_decompose(df_pred,period=period)
#日付・トレンド・周期・誤差の格納
df_pro_seasonal_decompose["order_date"] = res_pred.trend.index
df_pro_seasonal_decompose["trend"] = res_pred.trend.values
df_pro_seasonal_decompose["seasonal"] = res_pred.seasonal.values
df_pro_seasonal_decompose["resid"] = res_pred.resid.values
#平行移動用予測期間トレンド・周期・誤差の格納
df_pred_seasonal_decompose = df_pro_seasonal_decompose.query(("order_date >= '2017-01-01' & order_date <= '2017-12-31'"))
pred_trend = list(df_pred_seasonal_decompose["trend"])
pred_seaonal = list(df_pred_seasonal_decompose["seasonal"])
pred_resid = list(df_pred_seasonal_decompose["resid"])
else :
#最適化対象品種元データフレーム df_target
querystr = 'product_name == "' + pn_list[pn_index] + '"'
df_target = df_company1.query(querystr)
df_target = df_target.sort_values(by='order_date', ascending = True)
df_target = df_target.groupby('order_date').sum().reset_index()
df_target = df_target.query("order_date <= '2016-12-31'")
df_target = df_target.set_index("order_date")
df_ref_seasonal_decompose = df_pro_seasonal_decompose.copy()
df_ref_seasonal_decompose = df_ref_seasonal_decompose.query(("order_date <= '2016-12-31'"))
#過去需要の格納
df_ref_seasonal_decompose["quantity"] = list(df_target["quantity"])
#NA存在行削除
df_ref_seasonal_decompose = df_ref_seasonal_decompose.dropna()
#計算データ
#基準品番のトレンド・周期・誤差
ref_trend = list(df_ref_seasonal_decompose[-period:]["trend"])
ref_seasonal = list(df_ref_seasonal_decompose[-period:]["seasonal"])
ref_resid = list(df_ref_seasonal_decompose[-period:]["resid"])
#最適化品種の需要データ
pn_quantity = list(df_ref_seasonal_decompose[-period:]["quantity"])
#optuna
study = optuna_Trans(ref_trend,ref_seasonal,ref_resid,pn_quantity)
pred = (np.array(pred_trend) + study.best_params['m'] +
np.array(pred_seaonal) + study.best_params['n'] +
np.array(pred_resid) + study.best_params['l'])
#MAE比較パラメータ
df_test = df_company1.query(querystr)
df_test = df_test.sort_values(by='order_date', ascending = True)
df_test = df_test.groupby('order_date').sum().reset_index()
df_test = df_test.query("order_date >= '2017-01-01'")
#最適パラメータとMAEのテキスト出力
s = pickle.dumps(study.best_params)
d = pickle.loads(s)
with open(path, mode='a') as f:
f.write(pn_list[pn_index] + " 最適パラメータ : " + str(d) + "\n")
f.write(pn_list[pn_index] + " MAE : " + str(mean_absolute_error(df_test["quantity"],pred)) + "\n")
f.close()
#2017年との比較
fig,ax = plt.subplots()
ax.plot(list(range(period)),df_test["quantity"],color="b",label="actual")
ax.plot(list(range(period)),pred,color="r",label="pred")
ax.legend()
ax.set_ylabel("quantity")
ax.set_xlabel("Date")
fig.savefig('/content/compare/' +pn_list[pn_index] +"_2017compare.jpg")
MAEの結果は以下のようになりました。なお各クラスタリング手法の基準品番を黒太字に、各品種における最大値のセルをオレンジに、最小値を青にしています。つまり各クラスタリング手法の列における黒太字はNeuralProphetで15分学習した結果、それ以外の品種はクラスター番号に応じた基準品番の結果を平行移動した結果、前回記事はproduct 1のみNeuralProphetで学習した結果でそれ以外の品種はproduct 1の結果を平行移動した結果になっております。
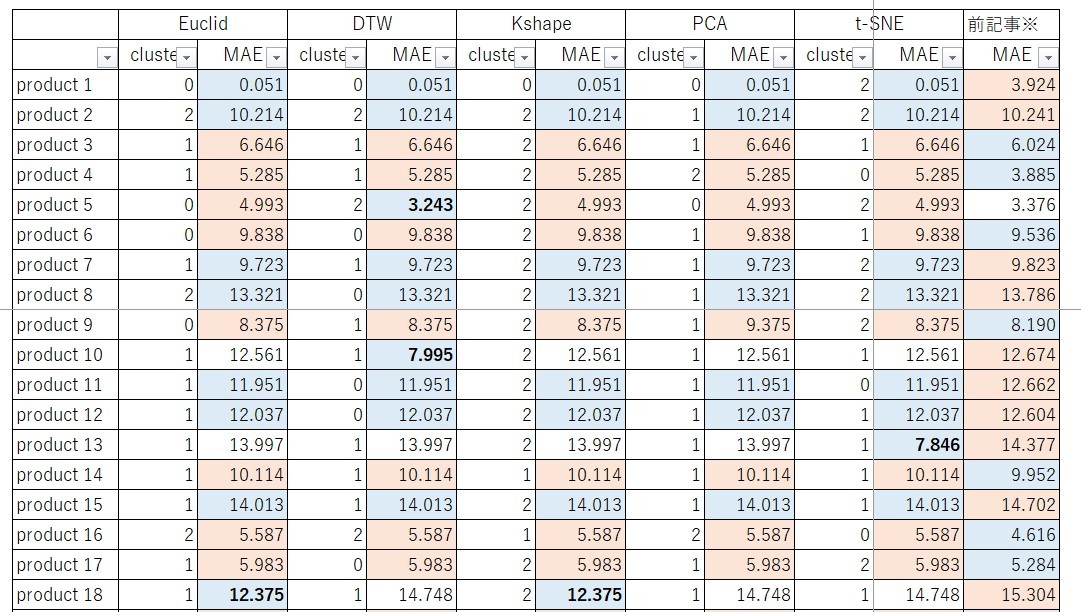

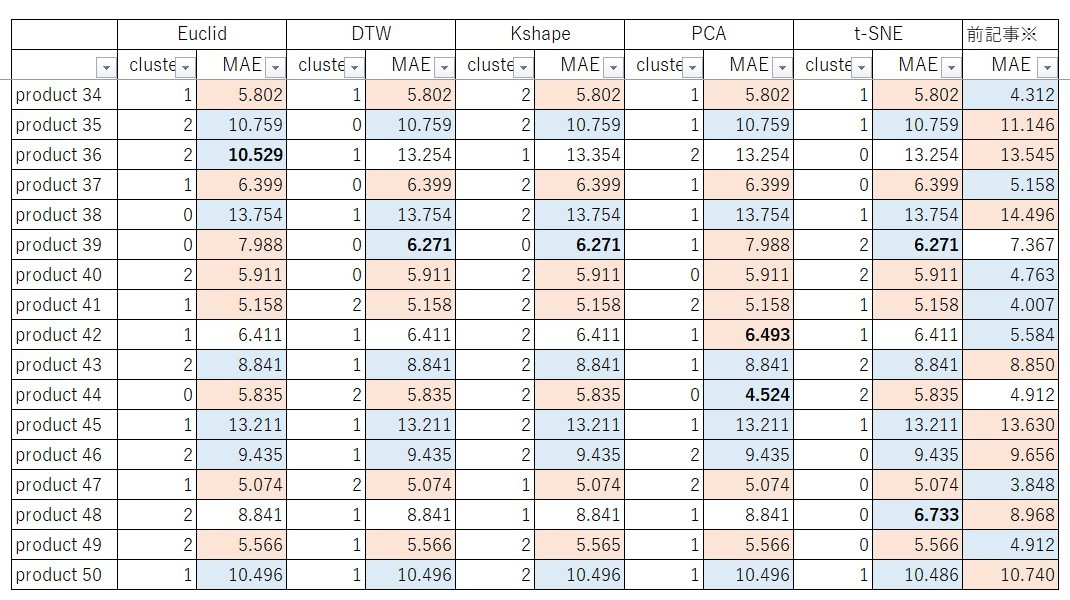
前回記事の方がMAEが大きい品番数(前回記事の方が予測精度が低い品番数)は24品番と半分近くありますが、前記事の方がMAが小さい品番に関しても21品番と同じ数だけあるように見えます。次に実際の需要と比較してます。例えば、前回記事と特にMAEに大きな差分があるk-shapeによるproduct 4とproduct34の需要を比較をすると、実際の需要と比較してもクラスタリング手法を適用しても問題ないように思います。
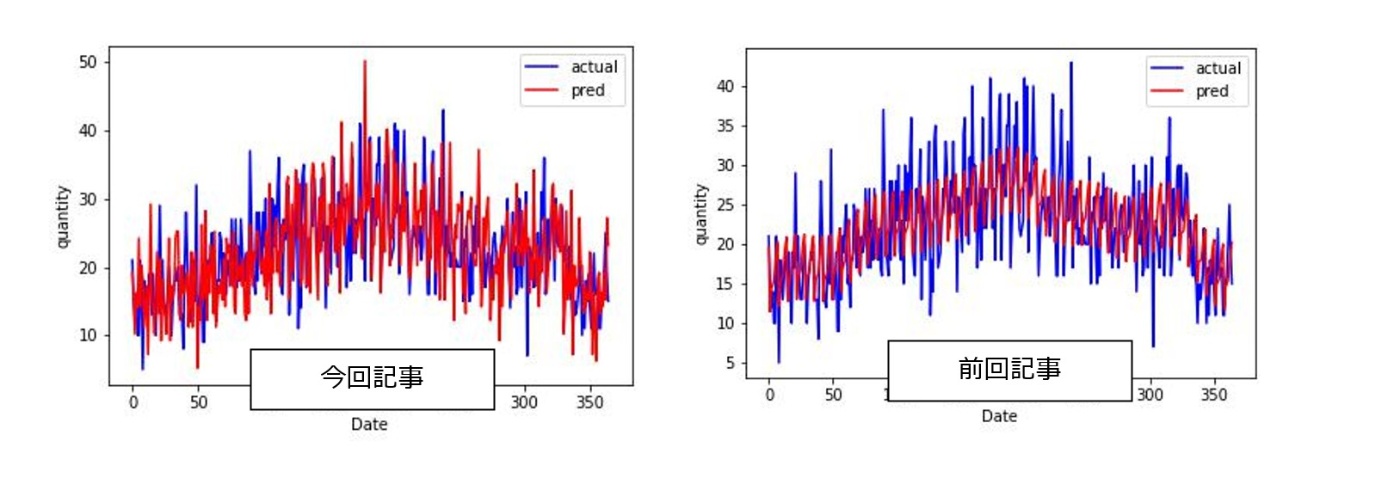
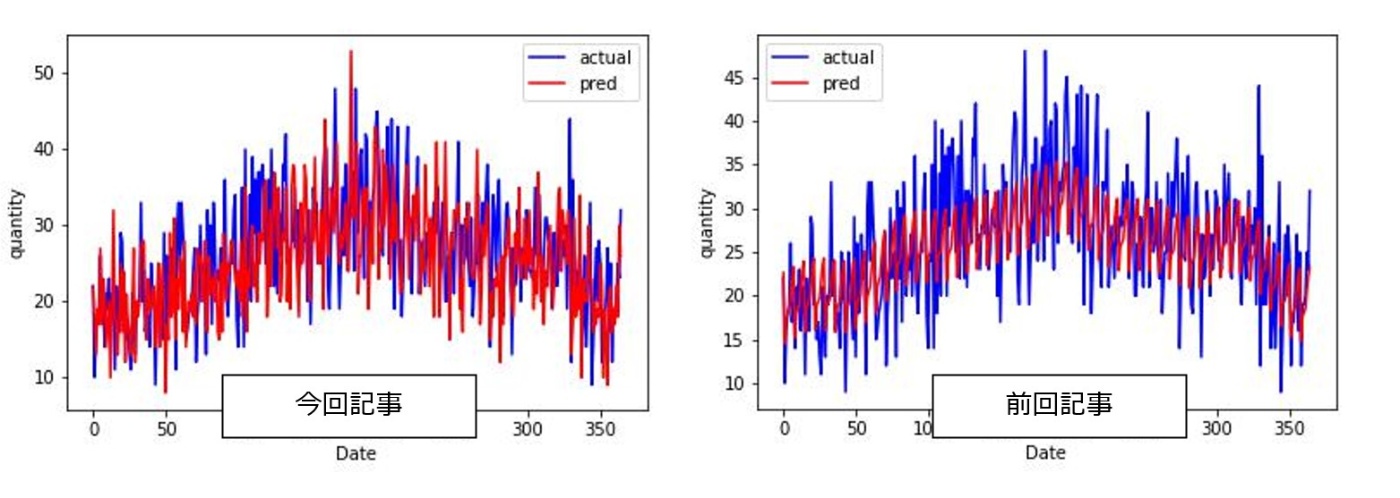
また前回記事で差分が大きかった品種もありましたが、そのような品番に対して多少の改善がみられております。例えば、product 15やproduct 28をみてみると、

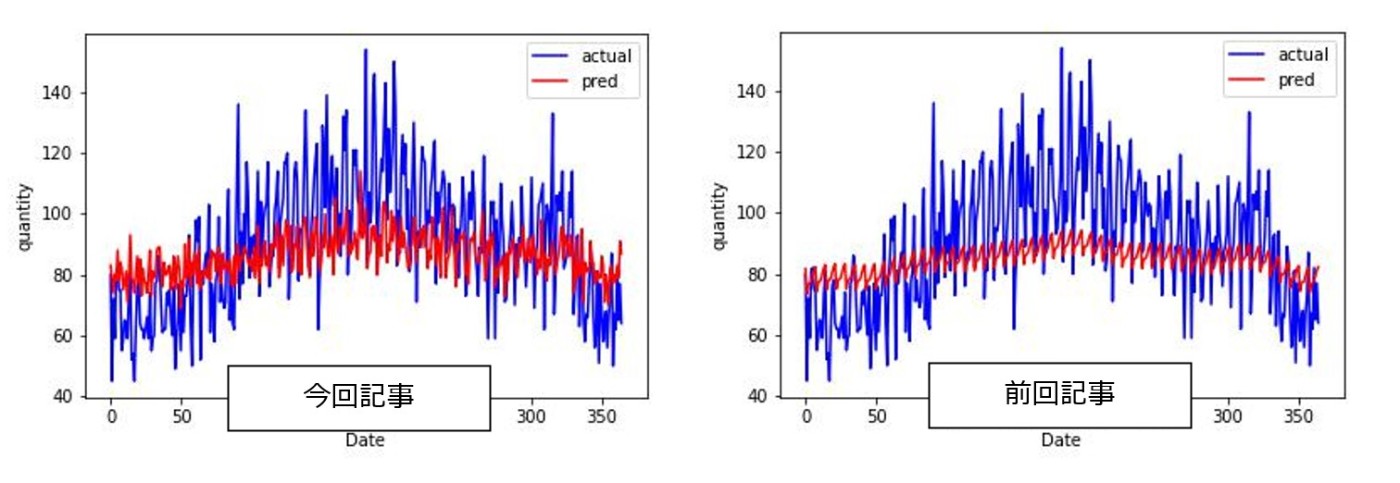
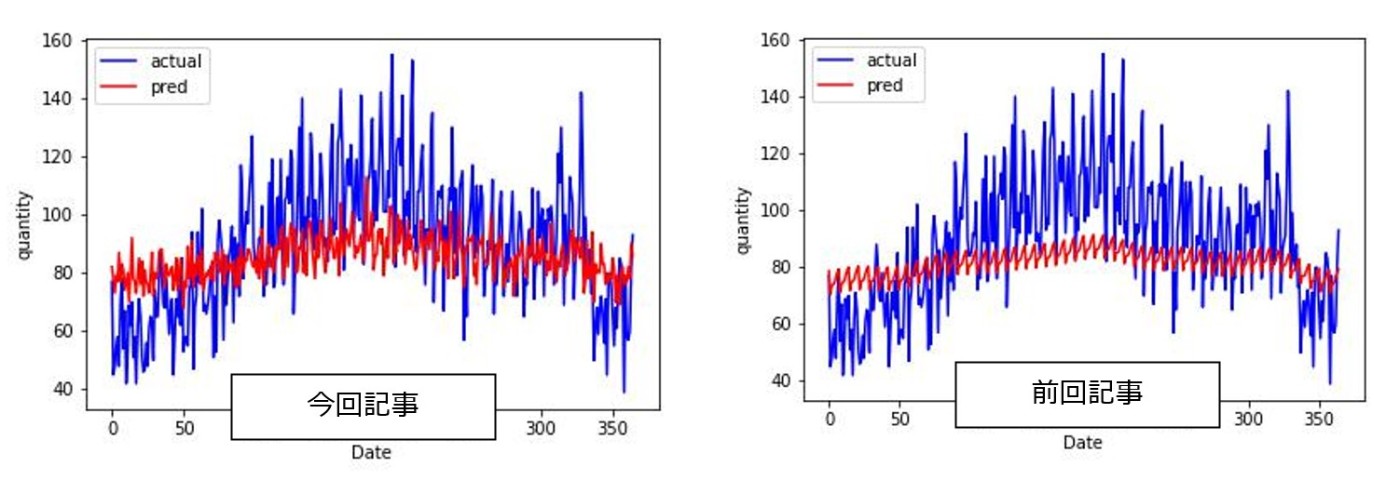
前回記事ではほぼ一定でしたが、今回は本当に少しですが、需要変動があるように思います。以上のことから、今回のような実装でクラスタリングを用いた基準品番の選定、そして、そこからの需要予測をすることは一定程度妥当性があるように思います。
しかしながら気になる点が2点あります。1点目は今述べ通りMAEの差分が大きい品種はあまり改善できていない点です。2点目は、クラスタリング手法の違いによりMAEの差が小さいことです(正確には小数点の桁数が大きくなれば差分は出ています)。そこで、各クラスタリングはあっているかを確かめるため、前回記事でMAEが大きい品種トップ5(product 15、 product18、 product 22、product 28、 product 38)に対して、各クラスタリングの基準品種の最適パラメータをそのまま流用する形で需要予測を実施しクラスタリングが合っているかを確認していきます。すると結果は以下のようになります。
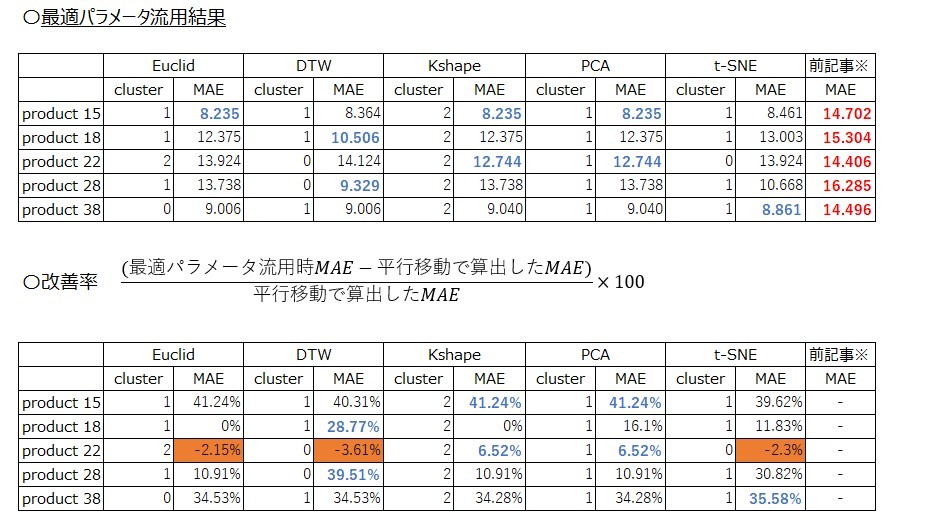
なお、k-shapeとPCAの値が全一致している理由は基準品種であるproduct 18とproduct 13が最適なパラメータが一致しているからです。なお、k-shapeにおいてもproduct 18が基準品種のクラスターにproduct 13が属しています。
基準品種と類似性がない場合同一パラメータを用いても需要予測が上手くできないと考えると、全ての品番において平行移動で算出した予測値より改善しているKshapeかPCAが、需要予測の観点で良いクラスタリング結果であると言えます。
以上より、SSEでの評価と組み合わせて考えると、今回のデータにおいて最も良いクラスタリング手法は、k-shapeであると考えます。
需要予測実装手順の考察
最後に以上の結果を受け、実際の需要予測を行う際にどのような実装を行うべきかを考えていきます。
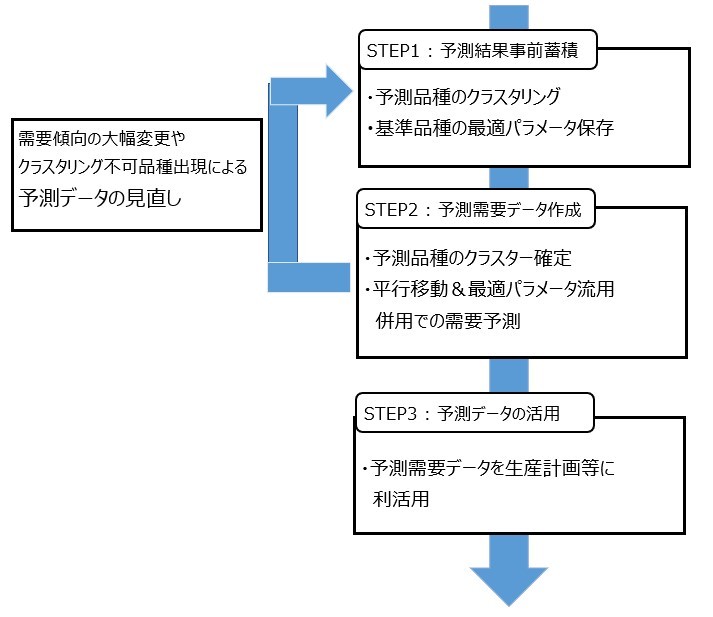
まず需要予測品種に対して、クラスタリングを実施し各品種がどのクラスターに属しているのか、および、どれを基準品種にすべきかを決定します。その後、基準品種のみ需要予測を実施し、最適パラメータやクラスタリング結果の情報をデータベースやcsvなどに保存します。またクラスタリングのfitデータの保存を実施しておきます。
続いて予測品種のクラスターを確定します。既にクラスタリングに属している品番は、基準品番の最適パラメータ情報に基づき需要予測を行っていきます。この際、基本的には平行移動の考え方を流用し予測していきます。理由は予測時間です。平行移動は1品種15秒程でしたが、NeuralProphetは45秒~1分程1品種にかかります。しかしながら、平行移動でも上手くできない品種はNeuralProphetを使った方がよいので、MAE等で閾値のようなものを決めておき、それ以上であればNeuralProphetを利用するという方法が良いと思います。まだクラスターが決まっていない品番に対しては、クラスターのfitデータを呼び出しクラスターを選定することで上記品番と同じように予測できます。
このような手順を取ることにより、需要傾向の大幅な変更、もしくは、新規品番の出現に伴うクラスタリングの再検討時のみ、最初のステップをやり直すことで、可能な限り時間をかけずに予測精度を担保した手法ができるのではないかと考えています。
今回の記事のまとめ、および、次回記事(予定)
今回の記事では、多品種の中から類似品種をまとめる方法として、時系列クラスタリングの学習と実装を行っていきました。具体的には、ユークリッド距離・DTWやk-shape、PCA/t-SNEを用いた次元削減からのk-mreans法を用いたクラスタリングを実装していきました。その結果、今回のデータにおいては、k-shapeが妥当ではないかという結果が得られました。
次回は内示情報を考慮した予測結果の変更方法の考察を行っていきたいです。
参考文献
〇前回記事
・Pythonの時系列解析手法(SARIMA、LSTM、NeuralProphet)実装と比較
・変動要因に類似点がある時系列データの需要予測に対する考察
〇各クラスタリング全般で使用
・見て試してわかる機械学習アルゴリズムの仕組み 機械学習図鑑,amazon 書籍
・機械学習ナビ
・Saeed Aghbozorgiら, Time-series clustering- A decade review, 2015
・白瀧豪ら,電力需要予測に対するモベルベース時系列クラスタリングの応用, 2018
・telearnを使って気象データをクラスタリングしてみる
〇Euclid/DTW
・時系列データのクラスタリング
・DTW(Dynamic Time Warping)/動的時間伸縮法について話す
・Time Series Clustering — Deriving Trends and Archetypes from Sequential Data
・tslearn.metrics.dtw
〇k-means法
・【機械学習】クラスタリングとは何か(k-means)
・sklearn.cluster.KMeans
〇k-shape
・John Paparrizosら, k-shape:Efficient and Accuturate Clustring of Time Series,2015
・時系列クラスタリング手法のk-shapeの論文を一部読んでみた
・Kshape
〇t-SNE
・Leurens van der Maatenら, Visualizing Data using t-SNE,2008
・t-SNE解説
・【次元圧縮】t-SNE (t -distributed Stochastic Neighborhood Embedding)の理論
Discussion