需要の先行情報を予測に活かす実装方法の考察

前記事までのまとめ、および、本記事の目的

前記事までは、多品種少量生産における需要予測手法の確立に向けて以下のことをしていきました。
・初回記事 : 時系列解析手法の実装と評価
　この記事では、Store Item Demand Forecasting Challengeのデータセットにおいて、Neuralprophetの手法が精度の高い手法であると評価しました。

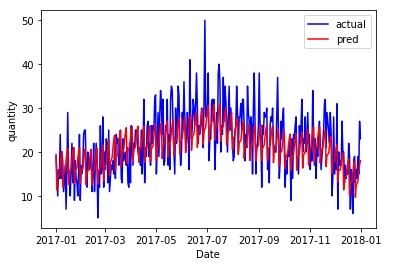
・第2回記事 : 時間をかけず多品種の需要を精度良く予測する手法の考察
　この記事の考察により、変動要因を除去した誤差成分に対してクラスタリングをしていき、品種をクラスターごとにまとめることにより、予測時間をかけずに精度の良い需要予測ができるのではないかという示唆が得られました。
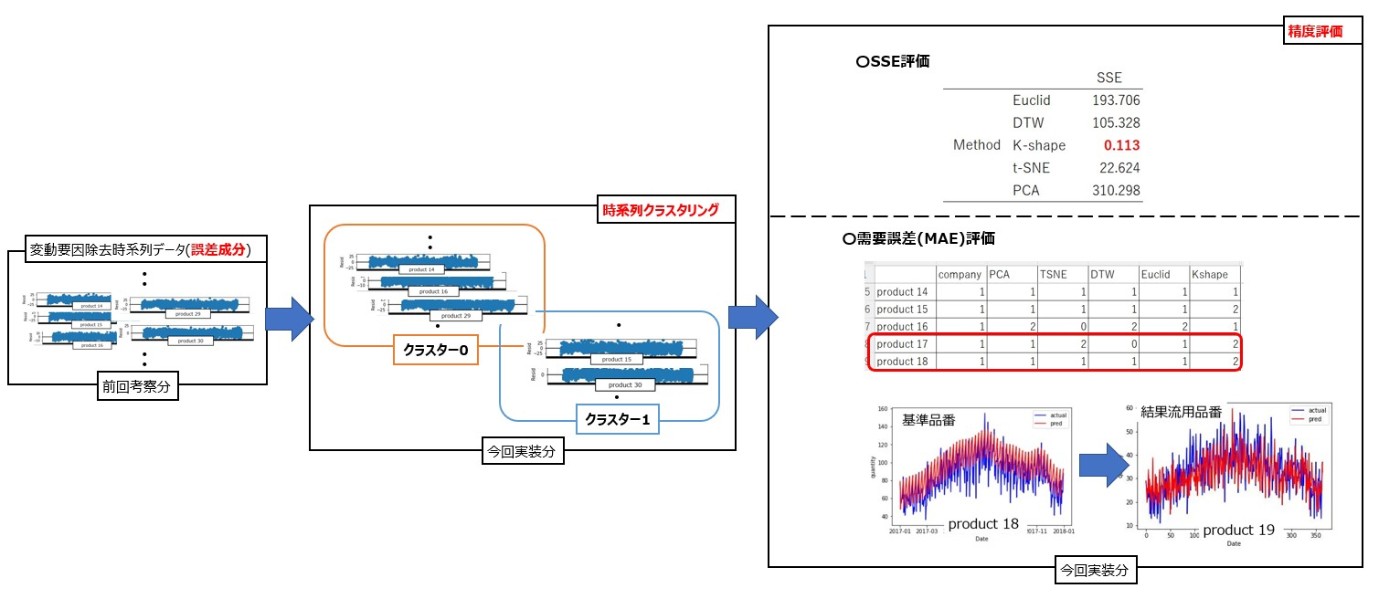
・第3回記事 : 時系列クラスタリングによる類似品種のクラスタリングの実装と評価
　上記結果を受け、時系列クラスタリングの実装方法を学習&評価しました。そして、どのような手順でクラスタリングを実施し、予測結果を出力すれば、可能な限り時間をかけずに精度の良い結果を。多くの品種に反映できるのかを考えていきました。


　さて、需要予測を考える際は内示のような先行情報(以下、Forcast)を用いることで事前に需要を把握し生産活動を実施する場合も存在します。この情報を用いて部材の手配等の作業を予め実施することにより、結果的にリードタイムを短縮することが可能になります。また、Forcastには今後の需要推移が反映されているため、過去データから推測できない情報が、Forcastに組み込まれていることも考えられます。例えば、過去需要の推移では減少傾向のあった品種が今後増加が見込まれているといった情報が組み込まれている場合、Forcastに沿って生産を実施することで、機会損失を防ぐことが可能です。しかしながら、Forcastが間違っていた場合、過剰な在庫を抱えることになります。このようにForcastが信頼できる値であるか、もしくは、どの程度補正をかければ信頼できる値と捉えることができるかが分からなければ、Forcastに基づく生産活動が実施することが困難です。
　過去のForcastを過去の予測データと捉えれば、過去の実需要と過去のForcastの比較方法として、MAEでの単純な比較、変動要因の分解、クラスタリング等を用いれば、過去のForcastが正確性を分析することが可能です。つまり、前記事までで学習したことを上手く組み合わせることができれば、Forcastの信頼性を評価し補正をかけることで需要予測に役立てる手法を提案できるのではないかと考えられます。
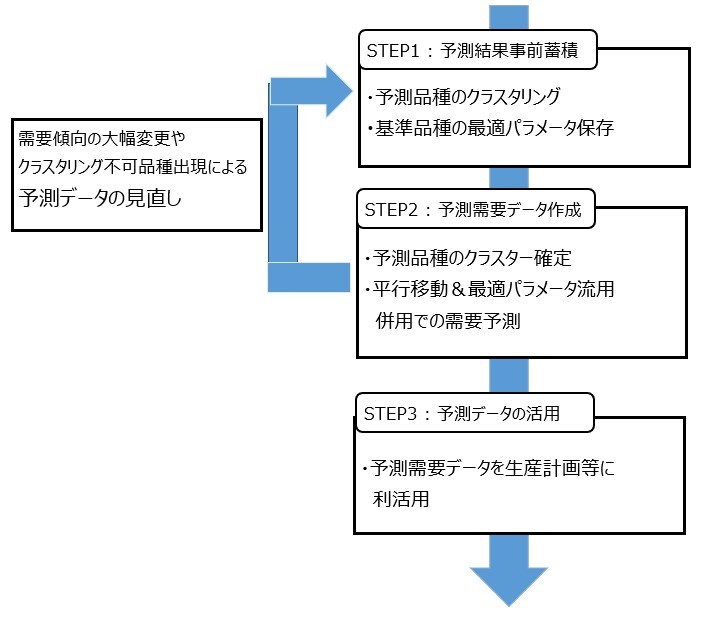
　そこで、本記事ではForcastを需要予測に反映させる手法として、Forcastの信頼性の評価方法、および、需要予測時補正の方法を考えていきます。具体的には以下の3ステップを考えています。第1ステップは、Forcastが実需要を上手く予測できているのかを、時系列クラスタリングを用いて評価するステップです。第2ステップは、実需要に対するForcastの補正値を求めるステップです。最終ステップは、Forcastに補正をかけて新たな予測結果を出力するステップです。

検証データ

実需要に関しては、Store Item Demand Forecasting Challengeのデータセットを用います。

　しかしながら、このデータにはForcastに対応するデータが存在しなかったため、後述の需要予測のズレ方を参考にノイズを加えたデータを作成し、Forcastとして考えます。

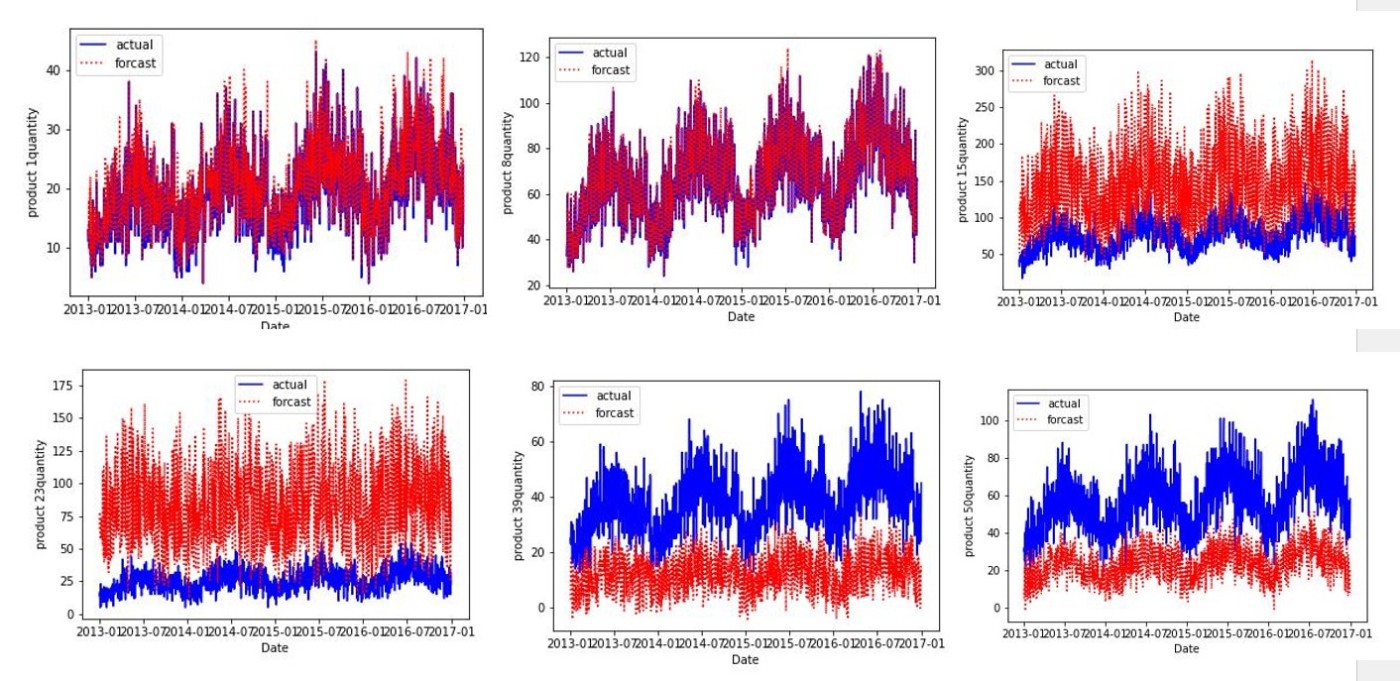
Forcastと実需要との差の分類

需要予測の結果は以下のように分類できると考えています。
・予測結果と実需要の一致率高い

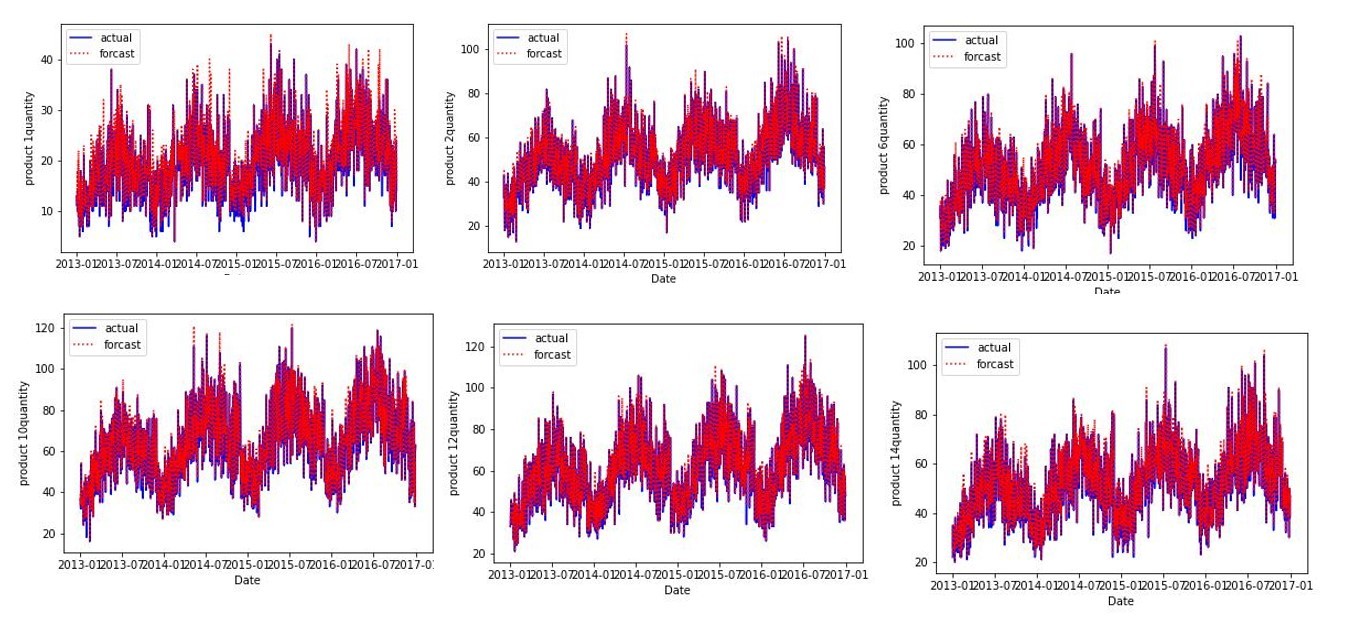
このForcastは信頼性の高い情報と捉えることが可能です。したがって、該当品種のForcastに対しては、補正をかけずに需要予測結果を上書きすることが妥当と捉えていきます。
・予測結果と実需要が一致率低い
　この分類に関しては一概に信頼性が低いとは言えないと考えています。理由は、全体としては差が大きいが類似性が見受けられるデータもあるからです。
例えば、以下のように周期性に関しては上手く予測はできているものの、値を小さく予測している、もしくは、反対に大きく予測していることもあると考えています。

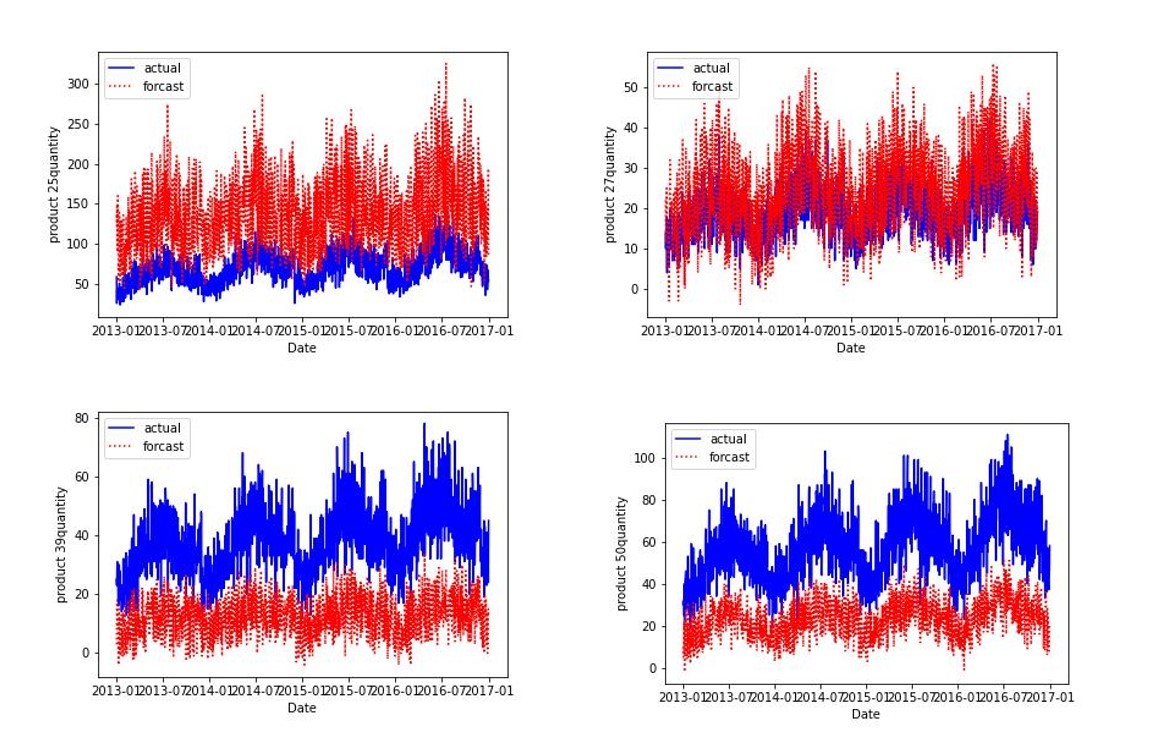
　上図のような例と全く予測から外れているデータを一致率が低いデータとして、ひとくくりにしてはいけません。上記のようなデータに対しては、Forcastに一定程度信頼性があると考え、補正をかけて需要予測データを作成するのがよいと考えられます。一方、周期性含めずれているデータはNeuralProphetのような需要予測手法を用いた予測結果を信用することに妥当性がありそうです。

本記事における需要の類似性の定義

前節の図から考えると、実需要との差だけで先行需要の信頼性を評価してはいけないと思われます。そこで、今回は需要の類似性を定義し、これに該当する品種は類似していると考えていきます。
時系列データは、長期変動要因(トレンド)・季節性要因(周期性)・誤差成分に分解できます。

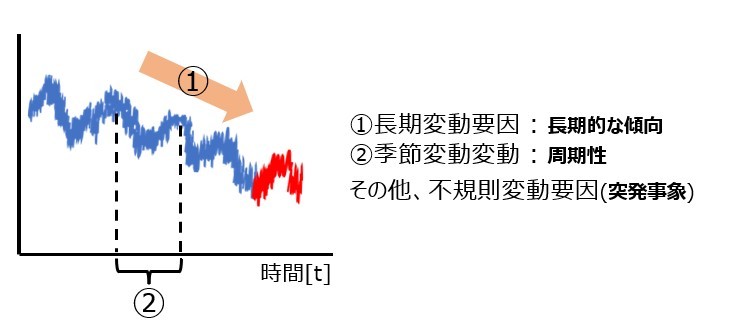
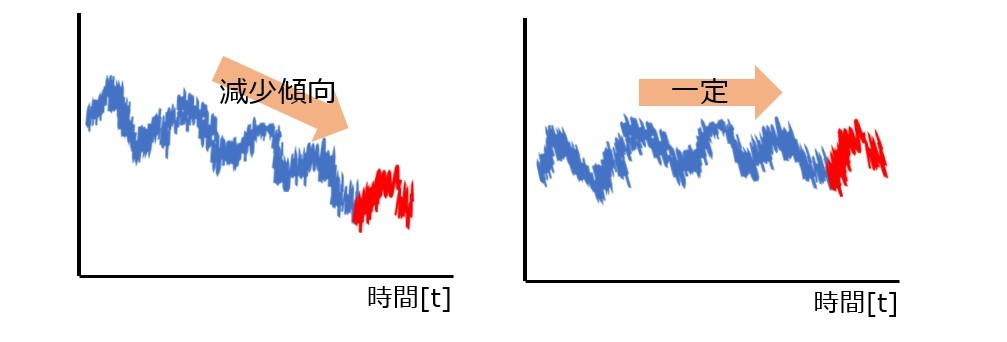
この各々の変動要因の傾向に類似性が見受けられる品種は類似の時系列データと考えることができます。特にデータの周期性や誤差に類似性があるデータは、グラフの可視化をしてもグラフに類似性があると考えられると思います。一方、トレンドに関しては需要の推移を示すものであり、あくまで推移の傾向の類似性を示すものだと思います。例えば、下図のような場合傾向に一致は確かに見られませんが、時系列データ自体には類似性があると捉えると思います。

　またトレンドを抽出し比較できれば値の補正をかけることも可能です。今回実装はしなかったですが、トレンドの関数を変更して予測データを作成することも実装は可能だと思われ、時系列データの類似性の観点において、周期性や誤差よりも類似性を考えなくてよい変動要因と考えられます。
　類似性のある品種は時系列クラスタリングの手法を用いて分類できます。例えば、実需要における誤差成分をk-shapeを用いてクラスタリングした結果は以下のようになります。なお、実装方法は公式ドキュメントを参考にしました。

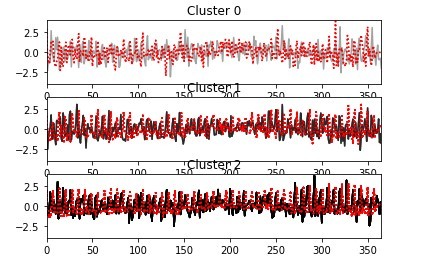
　このクラスタリングを行うにあたり、標準化・正規化を実施していきます。これにより、スケールの違いも考慮した類似性の抽出も可能となっています。すなわち、スケールが異なっていても推移が似ているデータは同一クラスターに分類され、類似データとしてまとめることができます。
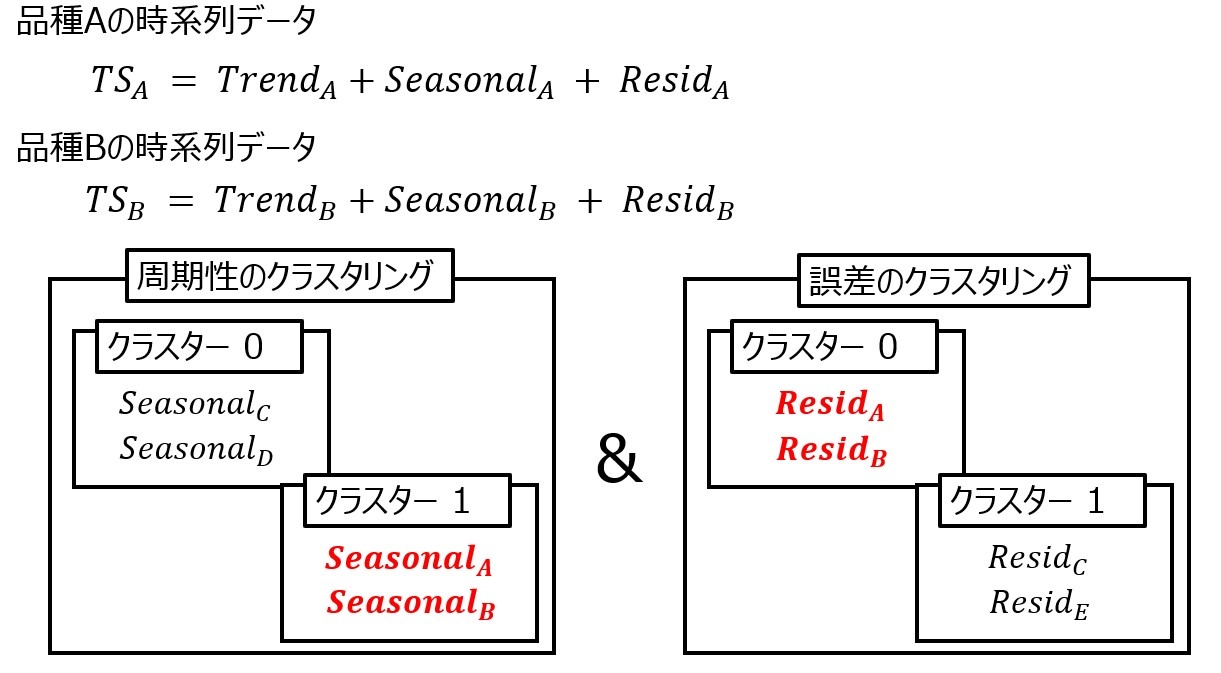
　以上より、ある品種Aと品種Bにおいて、需要の類似性が認められるという事象を以下のように定義します。
　品種Aの時系列データをTSA、品種Bの時系列データをTSBとし、トレンド成分をTrend、周期性成分をSeeasonal、誤差成分をResidとすると、周期性成分のクラスタリング、誤差成分のクラスタリングの双方において、同一クラスターに品種Aと品種Bが存在していることと定義します。

Forcastを需要予測に反映させるための手順

それでは、Forcastを需要予測に反映させる方法を実装していきます。具体的には、Forcastに対して変動要因の分解、および、クラスタリングの手法を用いて、Forcastに対する信頼性の判断、および、補正値の算出を考えていきます。
　まず、周期成分・トレンド成分のクラスタリングを実施し、実需要とForcastの類似性を判断していきます。
　続いて、類似性が判断できた品種はForcastに一定の信頼性があると捉え、過去の実需要との比較を実施し、各変動要因に対する補正値を求めていきます。
　最後に、予測を実施するForcastの期間において先程求めた補正値に基づき補正をかけます。
　なお本記事では2013年～2016年を過去データと捉えてクラスタリングや分析を実施し、2017年を予測期間としていきます。

STEP 1 : Forcastと実需要の類似性の判断

需要の類似性の節の定義により、ある品種の実需要とForcastの時系列データに対して周期性成分と誤差成分を抽出し、その各々でクラスタリングを実施し、双方の成分で同一クラスターかを判断する必要があります。ここで、MAEによる評価も取り入れ、誤差が小さいものは再度評価を実施できるようにしていきます。今回はt-SNEによる次元削減をしてK-means法衣を用いてクラスタリングする方法を採用しました。またt-SNEによる次元削減に対し、時間経過に対する情報を組み込むために、フーリエ級数の考えを用い、その係数に対して次元削減を考えていきました(参考url①、参考url②)
　フーリエ級数の実装例は以下の通りです。

fourier_func.py

from scipy.optimize import curve_fit

def fourier_func(x, *a):
    a = np.array(a)
　　　#周期 T  , 係数の組み合わせ参考値(fn)
    T, fn = a[-1], len(a) – 1
     #正弦と余弦の係数リスト
    a = a[:-1]
     ＃フーリエ級数の周期性の表現 omega
    omega = [2 * i * np.pi / T for i in range(1, fn // 2 + 1)]
    #フーリエ級数の合算
    summation = sum([a[2 * i - 1] * np.sin(omega[i - 1] * x) + a[2 * i] * np.cos(omega[i - 1] * x) for i in range(1,fn // 2 + 1)])
    s = a[0] + summation
    return s

例えば、周期性のフーリエ級数の係数を保存するデータフレームをdf_fourier_seasonalとすると、係数の保存は以下のように実装できます。

fourier_coeffs.py

#フーリエの初期値
period = 365
x = np.array(range(len(df_clustering_seasonal)))
fn = 100
T = period

df_fourier_seasonal = pd.DataFrame(index=forcast_list,columns=["season_coefficients"])
#forcast_list : Forcastが存在する品種Noを入れたリスト
for pro in forcast_list :
  #print(pro)
  # df_clustering_seasonal : Forcastが存在する品番の実需要、Forcastの周期性成分を格納したデータフレーム(標準化 or 正規化済み)
  seasonal_y = df_clustering_seasonal[pro].values

   #curve_fitのための変数格納
  seasonal_ini_params = np.concatenate(([np.mean(seasonal_y)], np.zeros(2 * fn),[T]))

   #curve_fitによるフーリエ級数の係数の格納(seasonal_coefficients)
  seasonal_coefficients,coefs = curve_fit(fourier_series, x, seasonal_y, p0=seasonal_ini_params)
  df_fourier_seasonal.at[pro,"season_coefficients"] = list(seasonal_coefficients)

#df_fourier_seasonal

ではt-SNEによる次元削減とクラスタリングを実装していきます。なお今回は2次元に削減し、4つのクラスターにクラスタリングしていきます。

TSNE_clustering.py

from sklearn.manifold import TSNE
from sklearn.cluster import KMeans


#t-SNEによる次元削除
n_components = 2
cluster_tSNE = TSNE(n_components=n_components, random_state=42).fit_transform(fourier_array)

#k-means
km = KMeans(n_clusters=4,
            n_init=20,
            max_iter=100,
            random_state=42)
# fit_predictメソッドによりクラスタリングを行う(Kmeans)
Y_km = km.fit_predict(cluster_tSNE)
TSNE_cluster_Kmeans = list(Y_km)

次に、クラスタリング実施時にMAEの評価軸も取り入れるため、誤差の小さいMAEの品種リストを作成します。今回は実需要の最小値の0.7倍の値以下の差を許容誤差として考えていきます。

MAE_errorlist.py

#minMAE_list : MAE比較リスト
minMAE_list = []

#df_forcast : 実需要とForcastデータが各品種ごとに入ってる
for i in range(len(df_forcast.columns.values) // 2) :
  #product 番号
  ori_pro = "product " + str(i+1) + " _1 Ori"
  forcast_pro ="product " + str(i+1) + " _1 Forcast"
  #MAE用データセット
  ori_y = list(df_forcast[ori_pro].values)
  forcast_y = list(df_forcast[forcast_pro].values)
  MAE = mean_absolute_error(ori_y,forcast_y)
　#今回の許容誤差 : 実需要の最小値の0.7倍の差分以下であること
  if MAE <= df_forcast[ori_pro].describe()["min"]*0.7:
    minMAE_list.append(i+1)

#MAE警告リスト
MAE_warninglist = []
#該当品番と品番数の表示
print(minMAE_list)
print(len(minMAE_list))

今回該当する品種は以下のようになります。

　では同一クラスターかを判断していきます。実装例は以下のようになります。

season_samelist.py

import pickle
# season_samelist : 周期性で同一クラスターになるリスト
season_samelist = []
season_notsamelist = []

path = '/content/params.txt'
#クラスター番号のログファイル作成
for i in range((len(TSNE_cluster_Kmeans) // 2)) :
  with open(path, mode='a') as f:
    f.write(str(i+1) +"組目 : " + "原系列 " + str(TSNE_cluster_Kmeans[i]) + " , Forcast " + str(TSNE_cluster_Kmeans[i+1]) + "\n")
  f.close()

  if str(TSNE_cluster_Kmeans[i]) == str(TSNE_cluster_Kmeans[i+1]) :
　　　　＃クラスター番号が実需要とForcastで同一クラスターが同一であれば、season_samelistに格納
    season_samelist.append(i+1)
  else :
    num = i+1
    #MAEが許容誤差以内であれば再評価のため、season_samelistに入れ直す
    if num not in minMAE_list :
      season_notsamelist.append(i+1)
    else :
      season_samelist.append(i+1)
      MAE_warninglist.append("product " +str(i+1))

print(season_samelist)
print(season_notsamelist)
print(len(season_samelist),len(season_notsamelist))
print("全体的には誤差は小さいが、一部誤差が大きい可能性がある品種",set(MAE_warninglist))

MAE_warninglistは、実需要とForcastが同一クラスターではなかったものの、差分(MAE)が小さかった品種のリストになります。したがって、全体を見たら差分が小さいが、周期成分に対しては誤差が大きい可能性がある品種と捉えることができます。

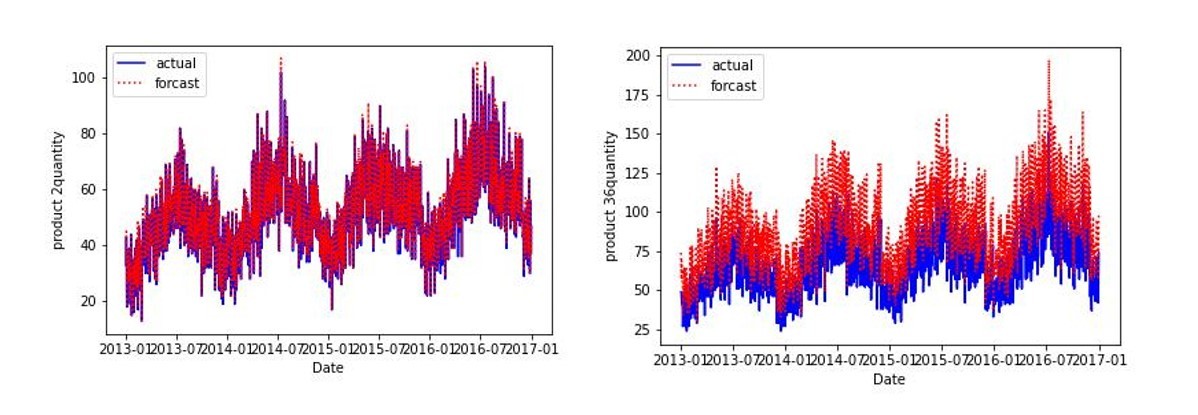
　今回はMAEの許容誤差を、実需要の最小値の0.7倍の差分以下であるとして進めており、その結果product 36のように、需要予測の上振れが大きい品種も評価対象に含んでしまっています。上振れが大きい品種を補正対象とするか、信頼せずNeuralProphetのような時系列解析手法の実装のデータを信頼するかは場合によると思います。したがって、上振れが高いデータ等外れ値が大きいデータも補正対象に組み込む場合は、許容誤差をデータに合った値を設定することが重要になります。
　周期性成分を抽出し実需要とForcastが「同一クラスターに属する品種、および、MAEによって再評価を判断した品種は、season_samelistに格納されています。そこで、season_samelistに対して同様の作業を誤差成分にもしていきます。誤差成分にも適用した結果は以下の通りです。


　上から以下のようなリストになっております。
・error_samelist : 周期性成分、および、誤差成分双方で「同一クラスターに属している、もしくは、STEP2で補正をかけるために再評価をする品種リスト
・error_notsamelist : 周期性成分の実需要とForcastが同一クラスターに属している一方、誤差成分は違うクラスターに属している品種リスト
・MAE_warninglist : 各クラスターにおいて、同一クラスターに属していないものの、MAEが小さいためSTEP2で再評価を試みようとする品種リスト

STEP2 : 実需要に対するForcastの補正値算出

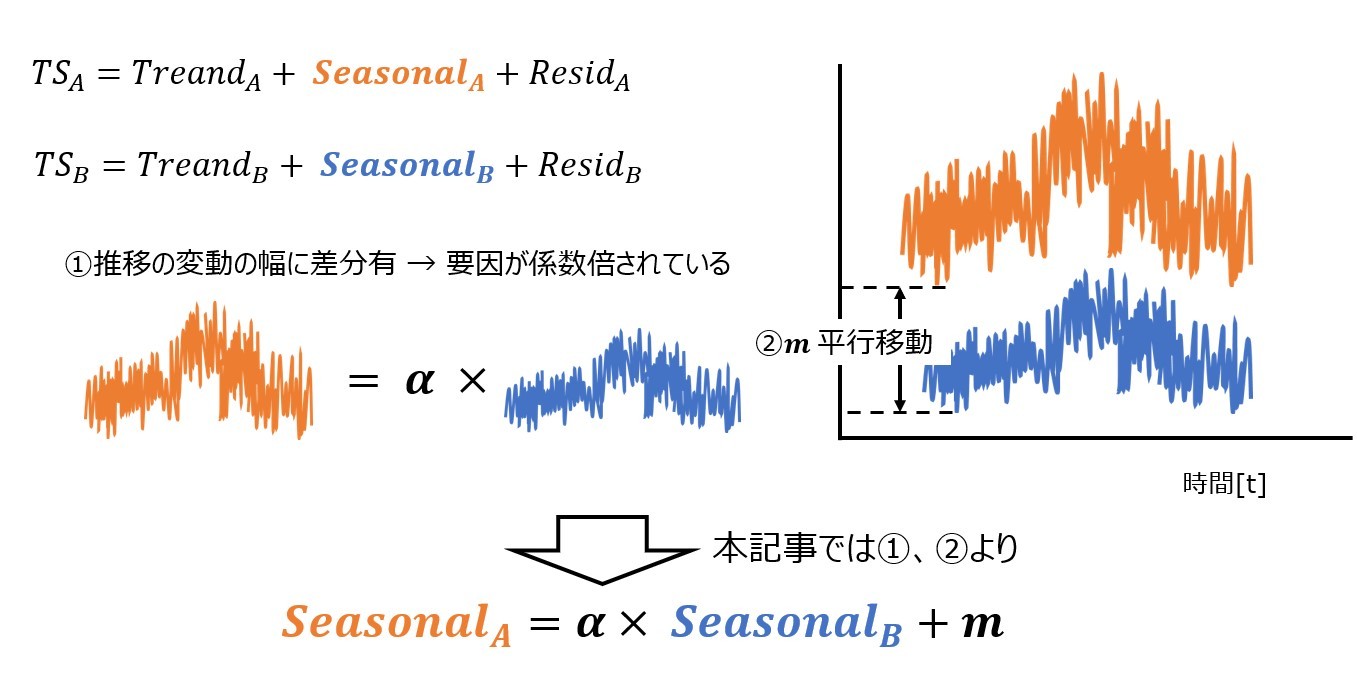
error_samelistの品種に対して、実需要とForcastの各変動要因を比較してForcastの補正値をも求めていきます。今回はスケールの違いを考慮したクラスタリング手法を用いており、同一クラスターはデータの推移に類似性はあるが、変動の幅には違いがあると考えられます。すなわち、Forcastの各変動要因をy軸上に平行移動させるだけでなく、Fprcastの各変動要因に対して係数倍をして変動の幅に補正をかける必要があると考えました。例えば、周期性に対して考えてみると、類似性のある品種は下図のようになるため、実需要とForcastにも同様の関係が成立すると考えることができます。

上図に対応した各変動要因に対する最適パラメータを求めるoptunaの実装は以下のようになります。

optuna_params.py

def Multiple_Trans_seasonal_decompose(sd,slope,intercept,valid) :
  upper_slope = slope[0]
  lower_slope = slope[1]
  upper_intercept = intercept[0]
  lower_intercept = intercept[1]
  def objective(trial) :
    #最適パラメータ候補設定
    params ={
        "alpha" : trial.suggest_float('alpha',upper_slope,lower_slope),
        "m" : trial.suggest_float('m',upper_intercept,lower_intercept),
    }
   #平行移動と係数分を考慮した予測値の算出
    pred = params["alpha"] * np.array(sd) + params['m']
    
    #valid(2016年までの変動要因との差分比較
    MAE = mean_absolute_error(valid,pred)
    return MAE
  
  return objective

study.py

def optuna_seasonal_decompose(sd,slope,intercept,valid):
  study = optuna.create_study(sampler=optuna.samplers.RandomSampler(seed=42))
  study.optimize(Multiple_Trans_seasonal_decompose(sd,slope,intercept,valid), n_trials=600)
  optuna_best_params = study.best_params
  return study

上記のoptunaで求めたパラメータに対して閾値を設け、その閾値以内であればForcastの値を適用するものとしていきます。また各変動要因に対し、実時需要とForcastの差分(MAE)が許容誤差の範囲内かどうかも判断し、この両方の条件を満たさないものは、Forcastの値が信頼できないものとして、値の補正値を格納していきます。すなわち、本記事における、Forcastの信頼性が高いとは、変動要因のMAEが許容誤差に収まっている、かつ、変動要因の補正に対する最適パラメータが閾値以内であることと定義し、以下のように実装していきます。

Is_BestParams.py

def Is_BestParams(optuma_params,ori_pn,forcast_pn,df_sd,thresholds,logpath) :
  #予測値
  sd = list(df_sd[forcast_pn].values)
  pred = optuma_params['alpha'] * np.array(sd) + optuma_params['m']
  
  #閾値
  MAE_rate = thresholds[0]
  lower_slope = thresholds[1]
  upper_slope = thresholds[2]
  ori_minq = thresholds[3]

  #strに変換させるためのロード
  s = pickle.dumps(optuma_params)
  d = pickle.loads(s)
  #MAE計算
  MAE = mean_absolute_error(df_sd[ori_pn],df_sd[forcast_pn])
  if df_sd[ori_pn].describe()["min"] > 0 :
    MAE_compare = df_sd[ori_pn].describe()["min"] * MAE_rate
  else :  
    MAE_compare = abs(df_sd[ori_pn].describe()["min"]) * MAE_rate
  with open(logpath, mode='a') as f:
    #最適パラメータログ出力
    f.write(str(ori_pn.split(" _1")[0]) + " 最適パラメータ : " +  str(d) + "\n")
    f.write(str(ori_pn.split(" _1")[0]) + " MAE閾値 : " + str(MAE_compare)  + "\n")
    #最適パラメータが閾値を超えている、もしくは、係数が閾値より大きければ、補正をかける、MAEを再計算
    if (MAE  > MAE_compare) and \
      ((study.best_params['alpha'] > upper_slope or study.best_params['alpha'] < lower_slope)  or \
      (study.best_params['m'] > ori_minq or study.best_params['m'] < -ori_minq)) :
        #再計算MAEログ
        reMAE = mean_absolute_error(df_sd[ori_pn],pred)
        f.write(str(ori_pn.split(" _1")[0])  + " のトレンドは元のデータの許容範囲外なので、最適パラメータを用いた補正を推奨します。\n")
        f.write(str(ori_pn.split(" _1")[0]) + " 再計算 MAE : " + str(reMAE) + "\n\n")
        #パラメータ適用
        Is_BestParams = True
    else :
        #MAEログ
        f.write(str(ori_pn.split(" _1")[0]) + " MAE : " + str(MAE) + "\n\n")
        #パラメータ適用なし
        Is_BestParams = False
  
  return Is_BestParams

それでは、補正値を求めていきます。今回は下記のようなデータフレームに格納し、csvに保存していきます。また2013～2016年までの実需要、Forcastの各変動要因に対して補正値を算出し、2017年のデータに対してその補正値を適用することを考えていきます。

　optuna.pyやIs_BestParams.pyを利用し以下のように実装できます。

Is_BestParams.py

trend_path = '/content/params_trend.txt'
seasonal_path = '/content/params_seasonal.txt'
resid_path = '/content/params_resid.txt'

for i in range(len(judgelist) // 6) :

  #optuna係数閾値設定
  lower_slope = 0.6
  upper_slope = 1.4
  slope = [lower_slope / 2 , 2 * upper_slope]

  ### トレンド成分 ###
  ori_pn_trend = judgelist[6*i]
  forcast_pn_trend = judgelist[6*i+1]

  #optuna切片閾値設定
  ori_minq = abs(df_sd[ori_pn_trend].describe()["min"])
  intercept = [-10 * ori_minq,10 * ori_minq]

  #optuna_trend
  valid_trend = list(df_sd[ori_pn_trend].values)
  forcast_trend = list(df_sd[forcast_pn_trend].values)

  study = optuna_seasonal_decompose(forcast_trend,slope,intercept,valid_trend)
  #pred = study.best_params['alpha'] * np.array(sd) + study.best_params['m']

  #トレンド適用判断
  trend_thresholds = [0.4,lower_slope,upper_slope,ori_minq]
  is_trend = Is_BestParams(study.best_params,ori_pn_trend,forcast_pn_trend,
                           df_sd,trend_thresholds,trend_path)
  trend_params = [study.best_params['alpha'],study.best_params['m']]

  ### トレンド成分 ###

  ### 季節性成分 ###
  ori_pn_seasonal = judgelist[6*i+2]
  forcast_pn_seasonal = judgelist[6*i+3]

  #optuna切片閾値設定
  ori_minq = abs(df_sd[ori_pn_seasonal].describe()["min"])
  intercept = [-10 * ori_minq,10 * ori_minq]

  #optuna_seasonal
  valid_seasonal = list(df_sd[ori_pn_seasonal].values)
  forcast_seasonal = list(df_sd[forcast_pn_seasonal].values)

  study = optuna_seasonal_decompose(forcast_seasonal,slope,intercept,valid_seasonal)
  #pred = study.best_params['alpha'] * np.array(sd) + study.best_params['m']

  #季節性適用判断
  seasonal_thresholds = [0.3,lower_slope,upper_slope,ori_minq]
  is_seasonal = Is_BestParams(study.best_params,ori_pn_seasonal,forcast_pn_seasonal,
                           df_sd,seasonal_thresholds,seasonal_path)
  seasonal_params = [study.best_params['alpha'],study.best_params['m']]

  ### 季節性成分 ###

  ### 誤差成分 ###
  ori_pn_resid = judgelist[6*i+4]
  forcast_pn_resid = judgelist[6*i+5]

  #optuna切片閾値設定
  ori_minq = abs(df_sd[ori_pn_resid].describe()["min"])
  intercept = [-10 * ori_minq,10 * ori_minq]

  #optuna_resid
  valid_resid = list(df_sd[ori_pn_resid].values)
  forcast_resid = list(df_sd[forcast_pn_resid].values)

  study = optuna_seasonal_decompose(forcast_resid,slope,intercept,valid_resid)
  #pred = study.best_params['alpha'] * np.array(sd) + study.best_params['m']

  #周期性適用判断
  resid_thresholds = [0.2,lower_slope,upper_slope,ori_minq]
  is_resid = Is_BestParams(study.best_params,ori_pn_resid,forcast_pn_resid,
                           df_sd,resid_thresholds,resid_path)
  resid_params = [study.best_params['alpha'],study.best_params['m']]

  ### 誤差成分 ###

  #パラメータ設定
  ori_pn = ori_pn_resid.split(" _1")[0]
  if not(is_trend) and not(is_seasonal) and not(is_resid) :
　　　#全て閾値以内なら補正なし
    df_productparams.at[ori_pn,"trend"] = [1,0]
    df_productparams.at[ori_pn,"seasonal"] = [1,0]
    df_productparams.at[ori_pn,"resid"] = [1,0]
  else :
    df_productparams.at[ori_pn,"trend"] = trend_params
    df_productparams.at[ori_pn,"seasonal"] = seasonal_params
    df_productparams.at[ori_pn,"resid"] = resid_params

#パラメータのcsv出力
df_productparams.to_csv("/content/seasonal_decompose_params.csv")

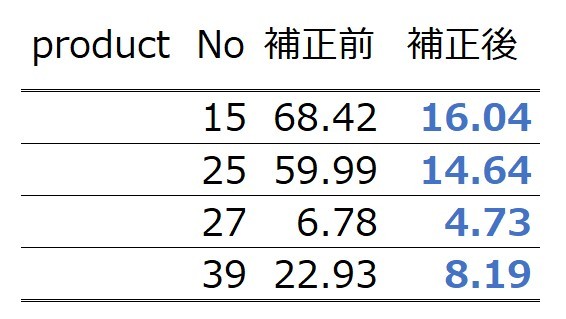
今回は、以下のような結果になりました。

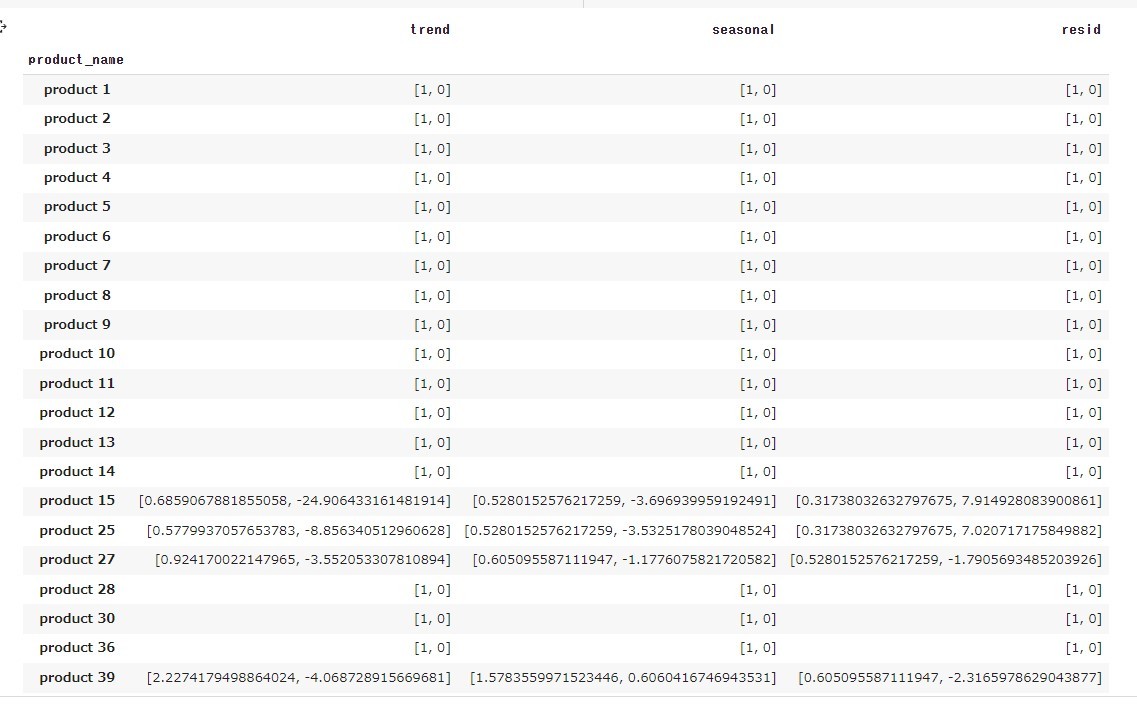
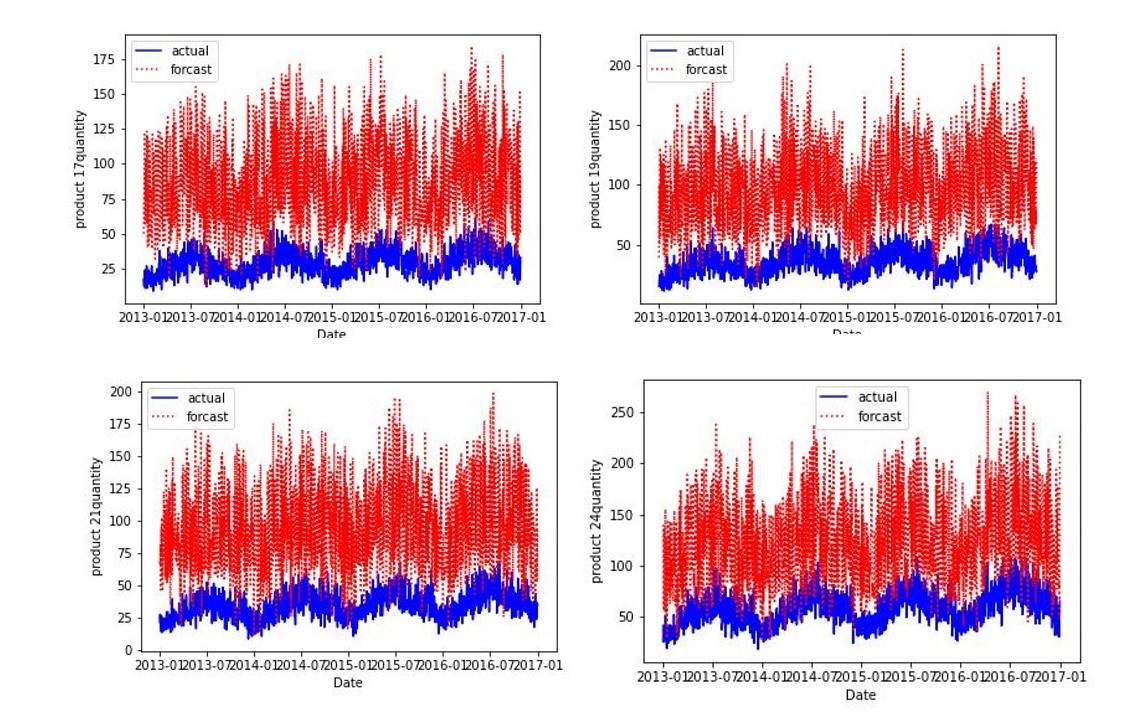
　この結果よりproduct1～14はForastの信頼性が高くForastの精度が良く、次の期間の予測に対しても補正をかけなくてよいという結論に至りました。実際この品種に対してはForcastの精度がよく、上手く分類できていると考えられます(例product3、product8、product 14)。

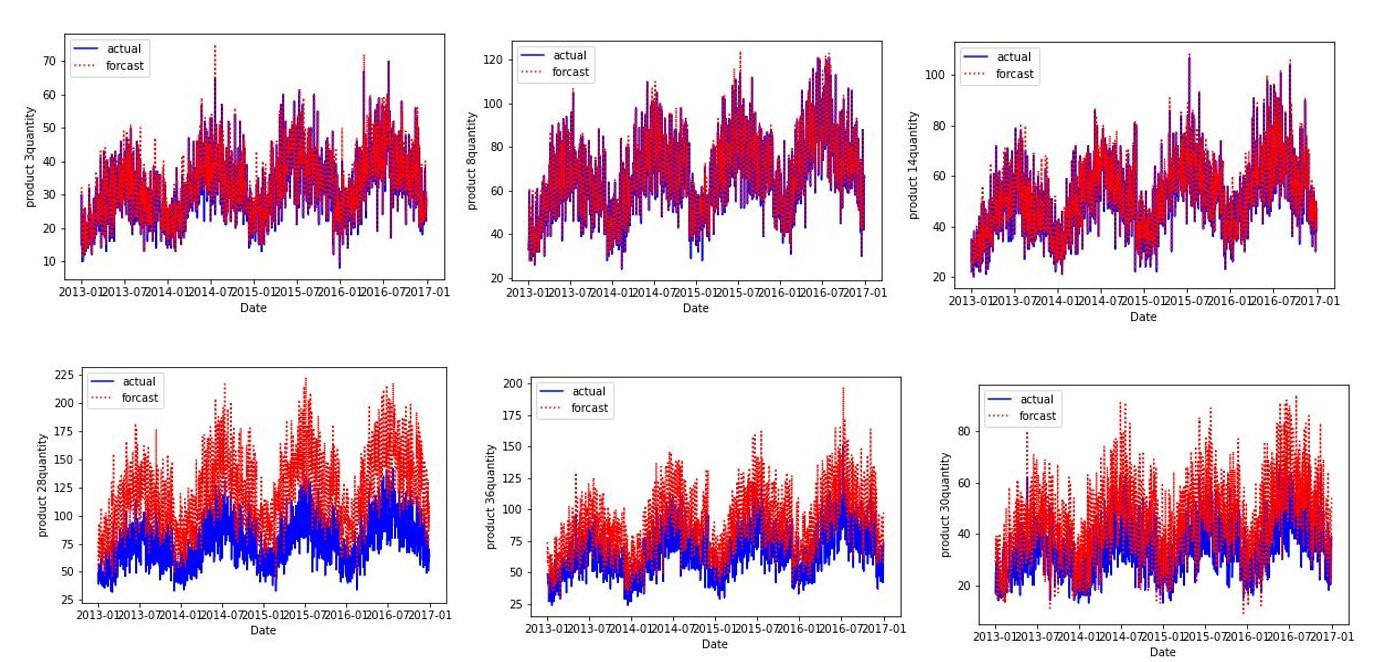
　一方、product 28、product 36、product30のように誤差が大きいものも補正をかけずにForcastの値を需要予測に利用するという結論になっており、許容誤差の値が緩いか、教養誤差の定義が正しくない可能性もあり、その点はまだ改善の余地がありそうです。
product 15、product 25、product 27、product 39に関しては補正値をかけて需要予測データを作成がするのが良さそうなので、次のステップでは補正値の適用をして、Forcastを修正していきます。

STEP3 : 補正値の適用によるForcastの修正

STEP2で求めた補正値を2017年のForcastの各変動要因に適用していきます。ここで、seasonal_decomposeによる分解では2017/12/31までの期間を指定しても分解の計算方法の都合上、途中の期間までのデータの要因のデータしか取得できません。

　そこで、得られる部分までのデータからcurve_fitによるフーリエ級数や多項式近似による係数取得方法を用いた上で、2017年度の各変動要因の時系列データの近似式を算出し、その近似に対して補正をかけることで、Forcastへの補正をかけていきます。なお、本記事では3次関数でトレンド成分の近似を行っています。
　3次関数のcurve_fitは以下のように実装できます。

Cublic_curve_fit.py

def Cublic_func(x,a,b,c,d):
  Y = a*np.array(x)**3 + b * np.array(x)**2 + c * np.array(x) + d
  return Y

続いてForcastの各変動要因の時系列データに対する係数を求めるための実装をしていきます。

Forecast_params.py

#フーリエ級数の使用変数
fn = 90
T = 365
#df_sd : 変動要因の値格納データフレーム
df_sd = pd.DataFrame(index=df_res.index,columns=["trend","seasonal","resid"])

for pn in df_productparams.index.values :
  corret_list = df_productparams.at[pn,"trend"]
  #各変動要因の補正値がすべて[1,0]であるとき(補正なし)の場合は、補正をかける必要がないため、
  #各変動要因データの関数近似をして、2017年(予測期間)のデータの近似値を求めなくてよい
  if not (df_productparams.at[pn,"trend"] == corret_list and df_productparams.at[pn,"seasonal"] == corret_list   and df_productparams.at[pn,"resid"] == corret_list) :
    forcast_pn = pn + " _1 Forcast"
    df_target = df_res[forcast_pn]

    print(pn)
    #変動要因分解
    res_target = sm.tsa.seasonal_decompose(df_target,period=period)
    df_copy = df_sd.copy()
    df_copy["trend"] = list(res_target.trend.values)
    df_copy["seasonal"] = list(res_target.seasonal.values)
    df_copy["resid"] = list(res_target.resid.values)
    df_copy = df_copy.dropna()
    #周期を反映させるために、前年から値を取得
    df_copy = df_copy["2016-01-01":]
    #変動要因のxとy
    x = np.array(range(len(df_copy)))
    trend_y = df_copy["trend"].values
    seasonal_y = df_copy["seasonal"].values
    resid_y = df_copy["resid"].values

    #トレンドの関数近似
    trend_coefficients,coefs = curve_fit(Cublic_func, range(len(df_copy)), trend_y)
    #print(trend_coefficients)
    new_trend_y = Cublic_func(range(len(df_copy)), trend_coefficients[0],trend_coefficients[1],trend_coefficients[2],trend_coefficients[3])

    #季節性の関数近似
    seasonal_ini_params = np.concatenate(([np.mean(seasonal_y)], np.zeros(2 * fn),[T]))
    seasonal_coefficients,coefs = curve_fit(fourier_series, x, seasonal_y, p0=seasonal_ini_params)
    new_seasonal_y= fourier_series(x, *seasonal_coefficients)
  
    #誤差の関数近似
    resid_ini_params = np.concatenate(([np.mean(resid_y)], np.zeros(2 * fn),[T]))
    resid_coefficients,coefs = curve_fit(fourier_series, x, resid_y, p0=resid_ini_params)
    new_resid_y= fourier_series(x, *resid_coefficients)

    #トレンド
    fig,ax = plt.subplots()
    ax.plot(range(len(df_copy)),df_copy["trend"],color="b")
    ax.plot(range(len(df_copy)),new_trend_y,color="r")
    plt.show()
    #季節性
    fig,ax = plt.subplots()
    ax.plot(range(len(df_copy)),df_copy["seasonal"],color="b")
    ax.plot(range(len(df_copy)),new_seasonal_y,color="r")
    plt.show()
    #誤差
    fig,ax = plt.subplots()
    ax.plot(range(len(df_copy)),df_copy["resid"],color="b")
    ax.plot(range(len(df_copy)),new_resid_y,color="r")
    plt.show()

    #df_coefficients : 各変動要因の係数格納データフレーム
    df_coefficients.loc[pn,"trend"] = trend_coefficients
    df_coefficients.loc[pn,"seasonal"] = seasonal_coefficients
    df_coefficients.loc[pn,"resid"] = resid_coefficients

以上の実装では、補正値をかけるための変動要因の近似と近似のための係数取得が可能です、
係数の結果は以下のようになります。

　各変動要因の近似例として、product 15のトレンド成分、周期性成分、誤差成分の近似結果を挙げます。



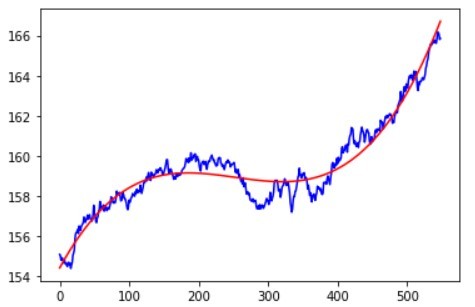
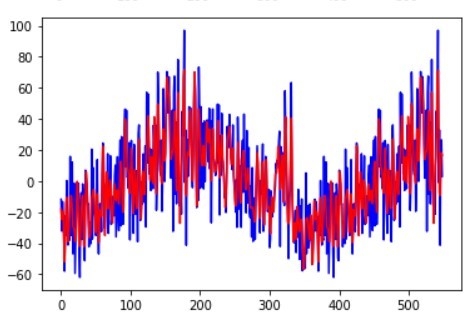
　この結果を見ると上手く各変動要因を近似できていることが分かります。では実際にForcastに対して補正をかけて需要予測への反映をしていきます。補正の実装方法例は以下の通りです。

Forcast_correction.py

import ast

#予測期間(2017年)の設定
start_2017 = len(df_copy) - len(df_copy["2017-01-01":])
end_2017 = start_2017 + 365
x = np.array(range(start_2017,end_2017))

for pn in df_coefficients.index :
  ori_pn = pn + " _1 Ori"
  forcast  = pn + " _1 Forcast"
  #各変動要因の近似関数に対する係数
  trend_coefficients = df_coefficients.at[pn,"trend"]
  seasonal_coefficients = df_coefficients.at[pn,"seasonal"]
  resid_coefficients = df_coefficients.at[pn,"resid"]
  #各変動要因のyの値
  new_trend_y = Cublic_func(x, trend_coefficients[0],trend_coefficients[1],trend_coefficients[2],trend_coefficients[3])
  new_seasonal_y = fourier_series(x, *seasonal_coefficients)
  new_resid_y = fourier_series(x, *resid_coefficients)

  #トレンド成分の補正
  trend_list = ast.literal_eval(df_productparams.at[pn,"trend"])
  new_trend_y = trend_list[0] * new_trend_y + trend_list[1]

  #周期性成分の補正
  seasonal_list = ast.literal_eval(df_productparams.at[pn,"seasonal"])
  new_seasonal_y = seasonal_list[0] * new_seasonal_y + seasonal_list[1]

  #誤差成分の補正
  resid_list = ast.literal_eval(df_productparams.at[pn,"resid"])
  #print(resid_list[0],resid_list[1])
  new_resid_y = resid_list[0] * new_resid_y + resid_list[1]

  #補正したForcast
  new_y = new_trend_y + new_seasonal_y + new_resid_y

  #実需要の値
  df_target = df_forcast[ori_pn]
  df_target = df_target[-period:]

  #グラフ描画
  print(pn)
  print("補正前MAE : ", mean_absolute_error(df_forcast[forcast_pn][-period:],df_target.values))
  print("補正後MAE : ",mean_absolute_error(new_y,df_target.values))
  #補正前
  fig,ax = plt.subplots()
  ax.plot(range(period),list(df_target.values),color="b",label="actual")
  ax.plot(range(period),list(df_forcast[forcast_pn][-period:]),color="r",label="forcast",linewidth=2,linestyle="--")
  ax.legend()
  ax.set_ylabel("quantity")
  ax.set_xlabel("Date")
  plt.show()
  #Forcast補正後
  fig,ax = plt.subplots()
  ax.plot(range(period),list(df_target.values),color="b",label="actual")
  ax.plot(range(period),new_y[-period:],color="r",label="forcast",linewidth=2,linestyle="--")
  ax.legend()
  ax.set_ylabel("quantity")
  ax.set_xlabel("Date")
  plt.show()

補正前後のForcastを見てみると、以下のようになります。




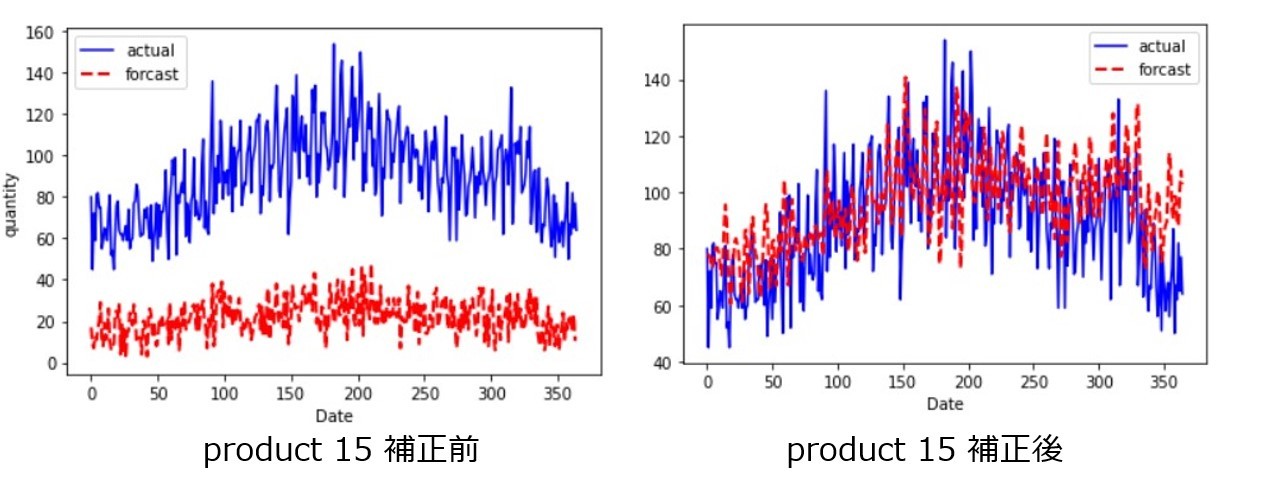
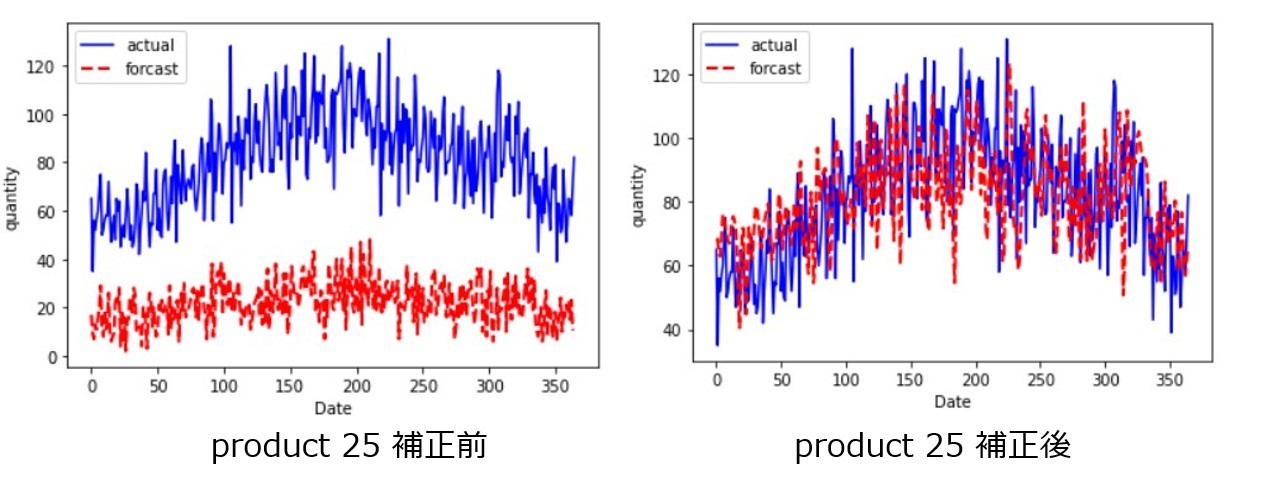
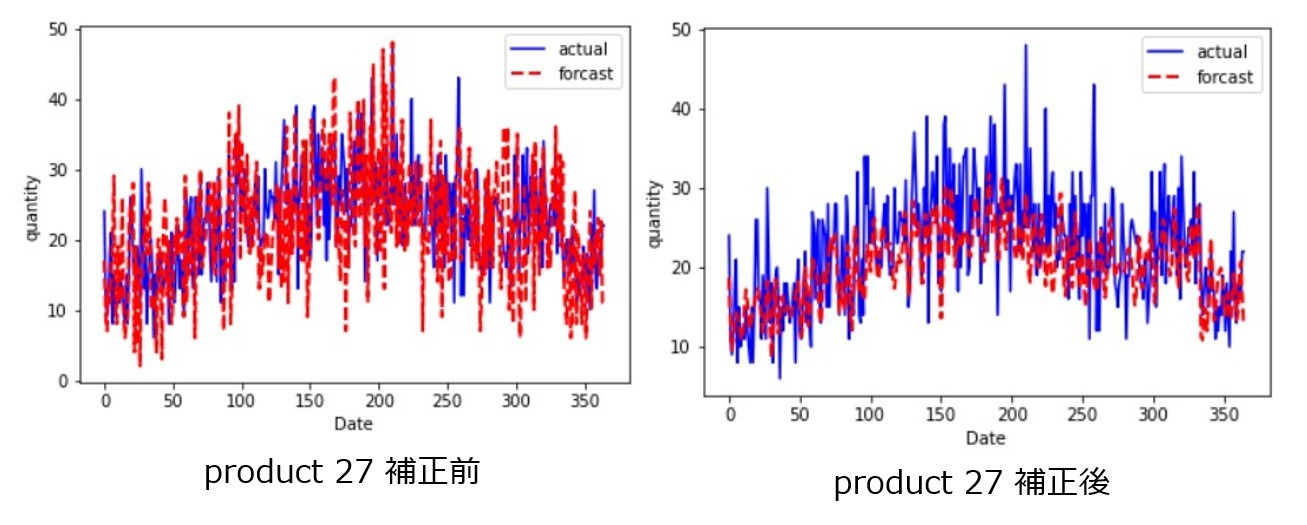
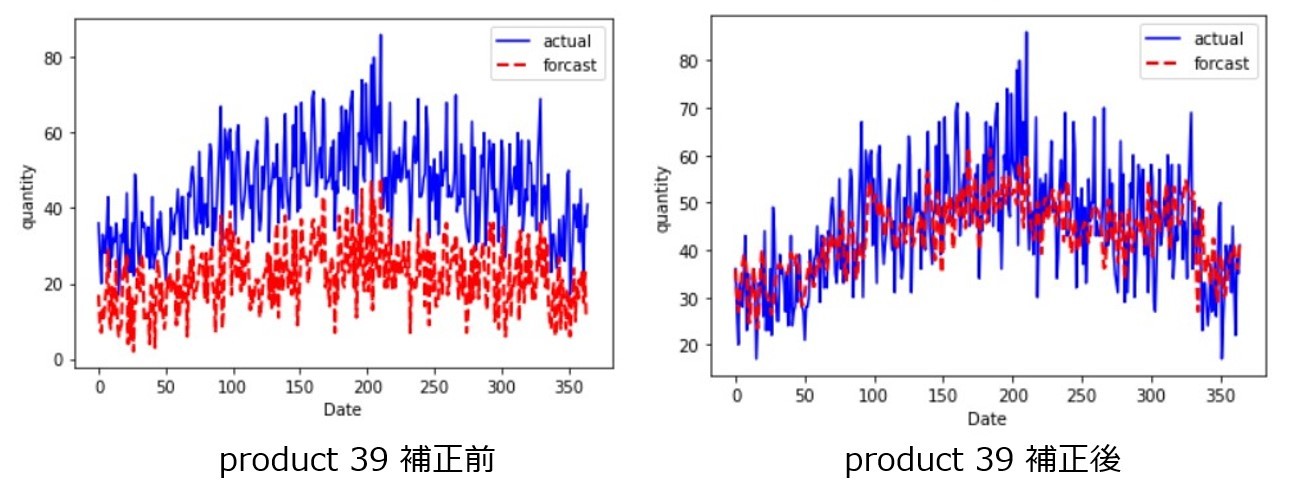
　結果を見ると、Forcast結果を活かしつつ補正値をかけることでForcastの需要予測を精度良いデータに修正することができました。MAEの観点でみても、補正後の方が良いことが分かります。

本記事のまとめ、および、次回記事内容(予定)

本記事は、需要の先行情報を活かした需要予測手法として、需要データに対して変動要因の分解、および、クラスタリングの手法を用いて需要の先行情報の補正の方法を考えていきました。その結果、補正をかけた品種に対しては差分が小さくなっていることが分かりました。一方、実需要との許容誤差が甘く、補正が上手くいかなかった例もあったので、そこの改善を検討する必要があります。次回以降で許容誤差の最適化等も考慮できればと思っています。また、信頼性が低いと判断された品種において指定期間のデータは信頼できるというような事象は、期間の設定や、該当期間の値は必ず需要予測に反映できるようなカラム設定をすれば可能だと考えているので、そのような実装もできればと思っています、
　次回は、前回記事までの内容のまとめ記事として、同じデータセットにおいて顧客Noが違うデータに対して前回記事までの需要予測手法の実装をしていきたいと考えています。それが終わったら本でまとめられたらと思っています。

参考文献

〇内示関連について
・上野信行, 内示情報を用いた生産計画,2009
・高野将吾ら,内示が与える生産計画への影響, 2019

〇クラスタリングについて
・KShape

〇関数近似
・Pythonプログラミング(ステップ7・リスト・フーリエ級数)
・フーリエ級数展開の公式と意味
・カーブフィッティング手法 scipy.optimize.curve_firの使い方を理解する
・scipy.optimize.curve_fit

〇前回記事まで
・私の記事ページ