Zenn
📊

[統計学] ポアソンの小数法則の証明と可視化

2023/04/16に公開
Python
data
math
機械学習
stats
tech

はじめに

この記事はポアソンの小数法則の証明と可視化を行なっている. なお, ポアソン分布の性質については下記の記事にまとめている.

ポアソンの小数法則

以下が成り立つ.

\lim_{np=\lambda, n\rightarrow \infty} \binom{n}{x} p^x (1-p)^{n-x} \rightarrow \frac{\lambda^x}{x!} e^{-\lambda}.

証明

注意

以下に注意する.

\lambda = np と固定するとき, n \rightarrow \infty で, p \rightarrow 0.

指数関数のマクローリン展開

導出にあたり以下の式を用いるので先に証明する.

e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!} \cdots (1)

証明:

下記のマクローリン展開を実行する. なお, f^{k} はfのk回微分とする.

\begin{align*} f(x) &= \sum_{k=0}^{\infty} f^{(k)}(0) \frac{(x-0)^k}{k!} \\ &= \sum_{k=0}^{\infty} f^{(k)}(0) \frac{x^k}{k!} \end{align*}

上式において f(x)=e^x としたときに, \forall k \in \N, f^{k}(0)=1 が成り立つ. よって明らかに(1)式が成り立つ. なお, マクローリン展開の詳細については別記事でまとめたので必要に応じて参照されたい.
マクローリン展開の可視化 | Shundeveloper

左辺の変形

\begin{align*} \binom{n}{x} p^x (1-p) ^{n-x} &= \frac{n!}{x!(n-x)!} p^x (1-p) ^{n-x} \\ &= \frac{(np)^x}{(np)^x} \frac{1}{x!} \frac{n!}{(n-x)!} p^x (1-p) ^{n-x} \\ &= (np)^x \frac{1}{x!} \frac{n!}{(n-x)!} \frac{(p)^x}{(np)^x} (1-p) ^{n-x} \\ &= (np)^x \frac{1}{x!} \cdot \prod_{k=0}^{x-1} (n-k) \cdot \frac{1}{n^x} \cdot (1-p) ^{n-x} \\ &= (np)^x \frac{1}{x!} \cdot \prod_{k=0}^{x-1} \frac{(n-k)}{n} \cdot (1-\frac{np}{n}) ^{n-x} \\ &= (np)^x \frac{1}{x!} \cdot (1-\frac{np}{n}) ^{n} \cdot \prod_{k=0}^{x-1} \frac{(n-k)}{n} \cdot (1-\frac{np}{n}) ^{-x}. \end{align*}
  • 右辺第五行の総積に n^{-x} を入れる操作は, 総積の要素数が n-(n-x)=x になることを用いている

左辺を変形した式の極限をとる

\begin{align*} \lim_{np=\lambda,n\rightarrow\infty} \binom{n}{x} p^x (1-p) ^{n-x} &= \lim_{np=\lambda,n\rightarrow\infty} (np)^x \frac{1}{x!} \cdot (1-\frac{np}{n}) ^{n} \cdot \prod_{k=0}^{x-1} \frac{(n-k)}{n} \cdot (1-\frac{np}{n}) ^{-x} \\ &= \lim_{np=\lambda,n\rightarrow\infty} \lambda^x \frac{1}{x!} \cdot (1-\frac{\lambda}{n}) ^{n} \cdot \prod_{k=0}^{x-1} \frac{(n-k)}{n} \cdot (1-\frac{\lambda}{n}) ^{-x} \\ &\rightarrow \lambda^x \frac{1}{x!} \cdot e^{-\lambda} \cdot 1 \cdot 1 \\ &= \frac{\lambda^x}{x!} e^{-\lambda}. \end{align*}

可視化

証明ができたのでシュミレーションして近似ができることを確認する.

実験用コード

シュミレーションに使うクラスを作成.

import math
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import binom, poisson

class Poisson:
    def __init__(
        self,
        n_: float,
        lambda_: float
    ) -> None:
        """
            Explain
            ------
            constructor. create three property.

            Parameter
            ------
            self: Poisson
            n_: float
            lambda_: float
        """
        self.n_ = n_
        self.lambda_ = lambda_
        self.p_ =  self.lambda_/self.n_
    
    def plot(
        self,
    ) -> None:
        """
            Parameter
            ------
            self: Poisson
        """
        # create array for plot
        x = np.arange(0, 100, 1)
        binomial_list = [binom.pmf(k, n=self.n_, p=self.p_) for k in x]
        poisson_list = [poisson.pmf(k, self.lambda_) for k in x]

        # seaborn settings
        sns.set()
        sns.set_style('whitegrid', {'grid.linestyle': '--'})
        sns.set_context('talk', 0.8, {'lines.linewidth': 0})
        sns.set_palette('GnBu', 2, 0.9)

        # make plot title
        basic_title: str = 'Binomial -> Poisson'
        n_info = ' (n = ' + str(round(self.n_, 4))
        p_info = ' p = ' + str(round(self.p_, 4))
        lambda_info = ' lambda = ' + str(round(self.lambda_, 4)) + ')'

        title = basic_title + n_info + p_info + lambda_info

        # plot
        fig=plt.figure(figsize=(16,9))
        ax1 = fig.add_subplot(1, 1, 1)
        ax1.set_title(title)
        ax1.set_ylabel('probability mass')
        ax1.bar(x, binomial_list)
        ax1.bar(x, poisson_list)
        ax1.legend(['binomial', 'poisson'])
        plt.show()
    
    def add_n(self, num: int) -> None:
        """
            add num to self.n_ and calc new self.p_

            Parameter
            ------
            self: Poisson
            num: int
        """
        if isinstance(num, int) is False:
            raise TypeError("type of num must be int")
        self.n_ += num
        self.p_ =  self.lambda_/self.n_

インスタンスを作成してポアソンの小数法則をシュミレーションする.

po = Poisson(n_=30, lambda_=15)
for i in range(3):
    po.plot()
    po.add_n(num=50)

結果

\lambda を固定しながら徐々に n を大きくして二項分布がポアソン分布に近づいている.

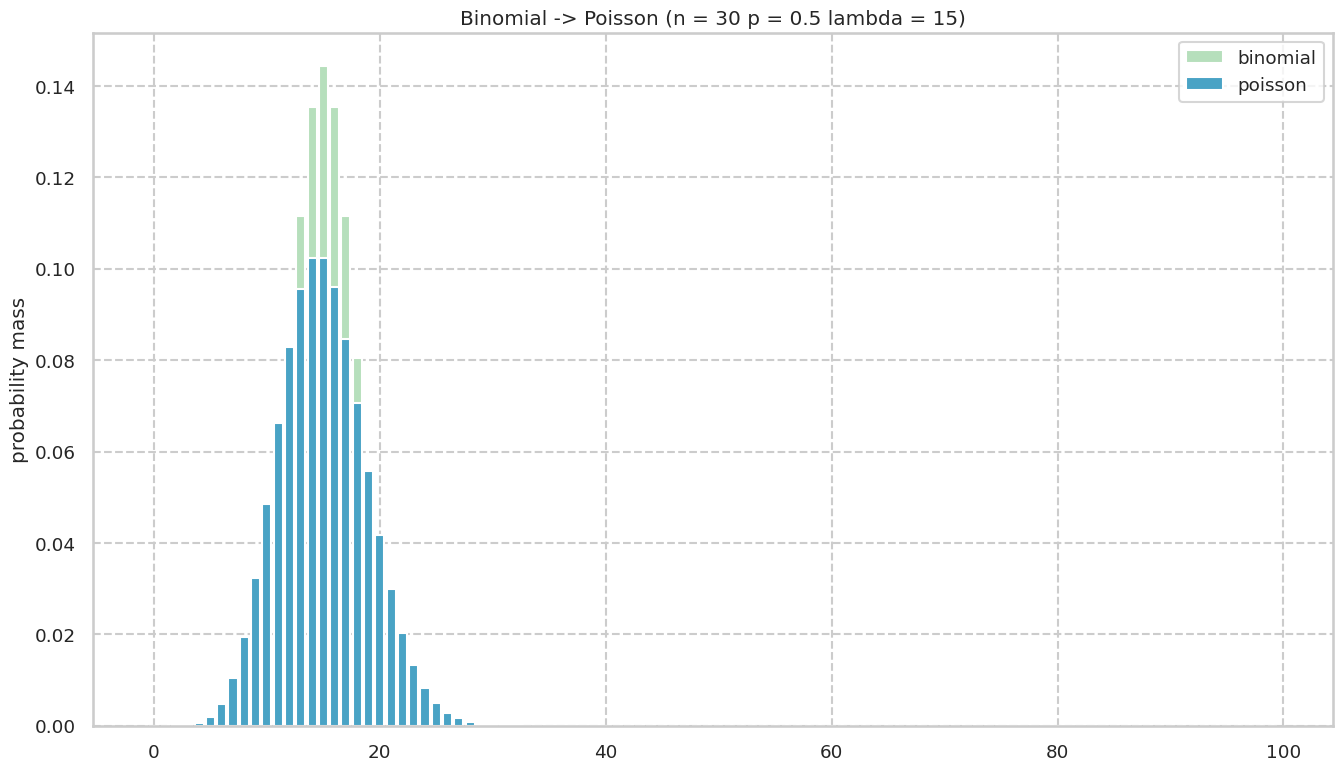
シュミレーション結果1
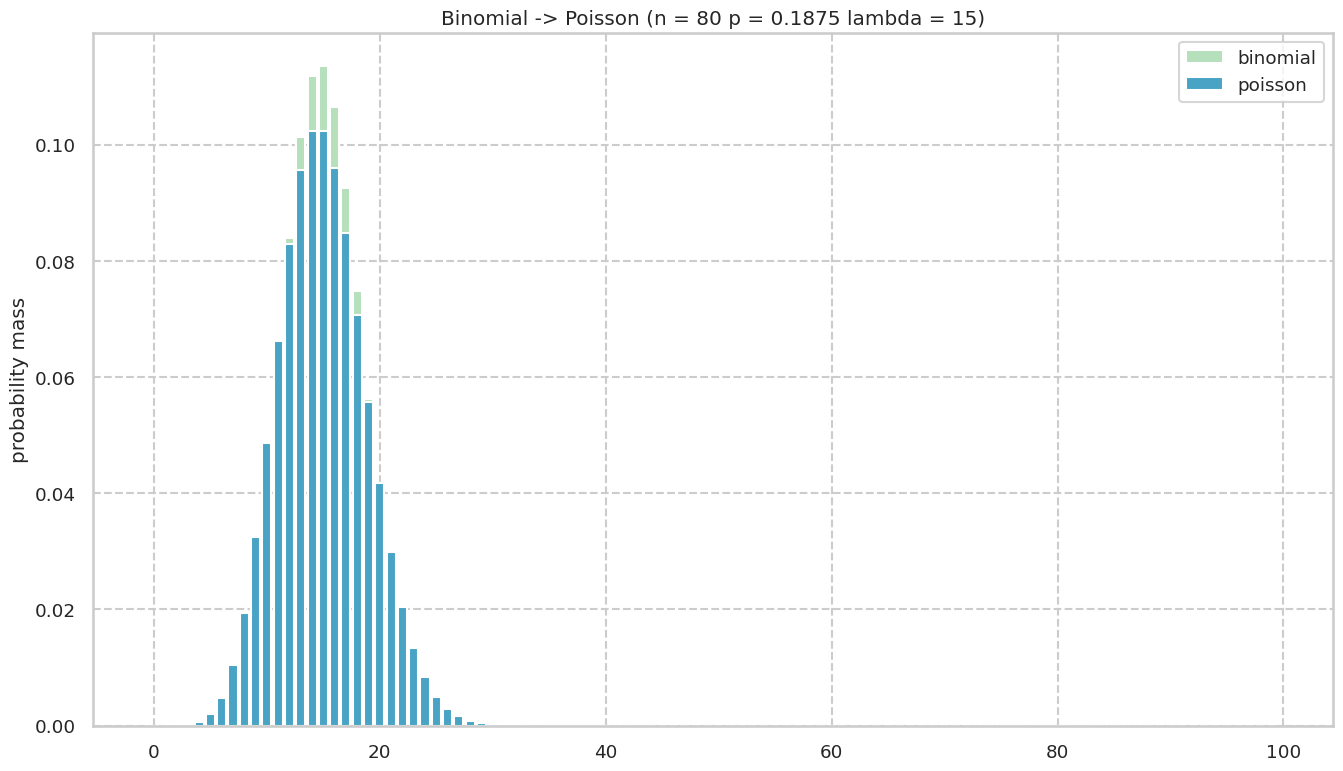
シュミレーション結果2
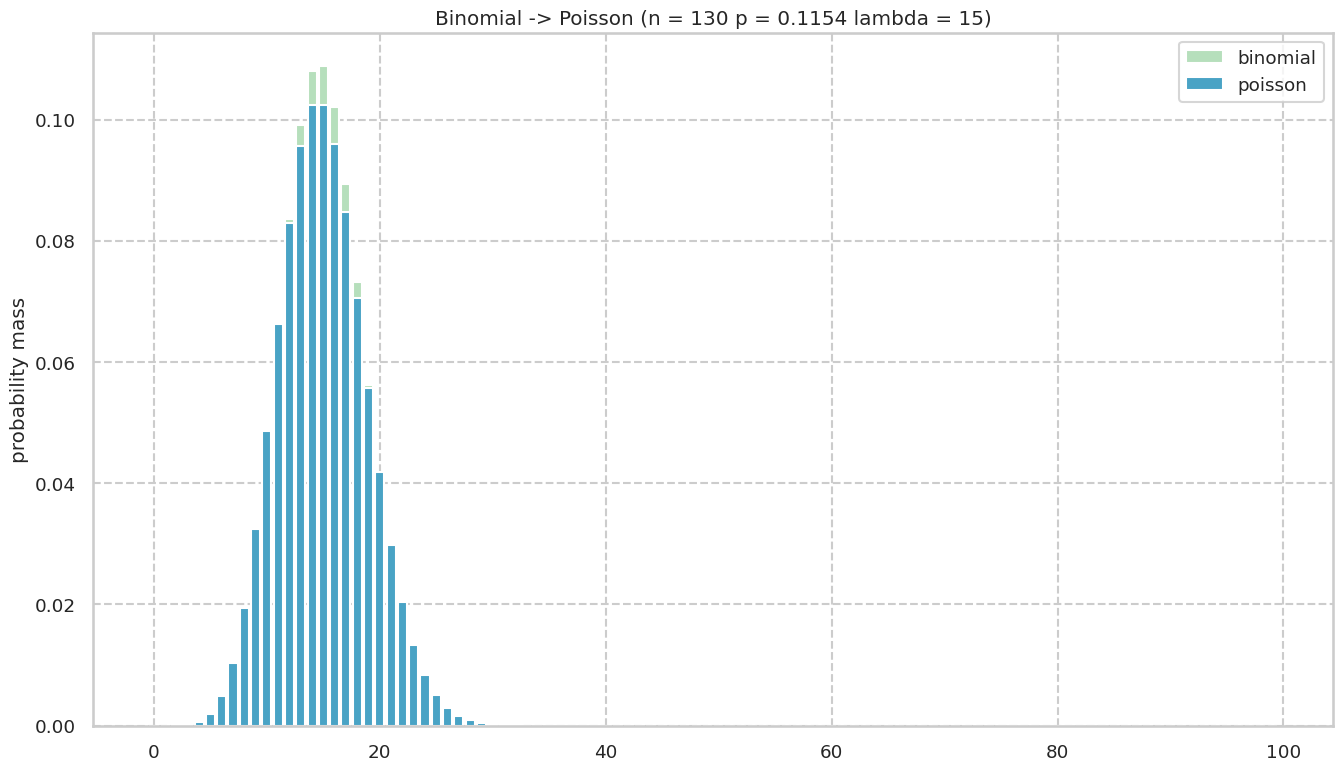
シュミレーション結果3

1000回にもなるとほとんど同じように見える.

po = Poisson(n_=30, lambda_=15)
po.add_n(num=1000)
po.plot()

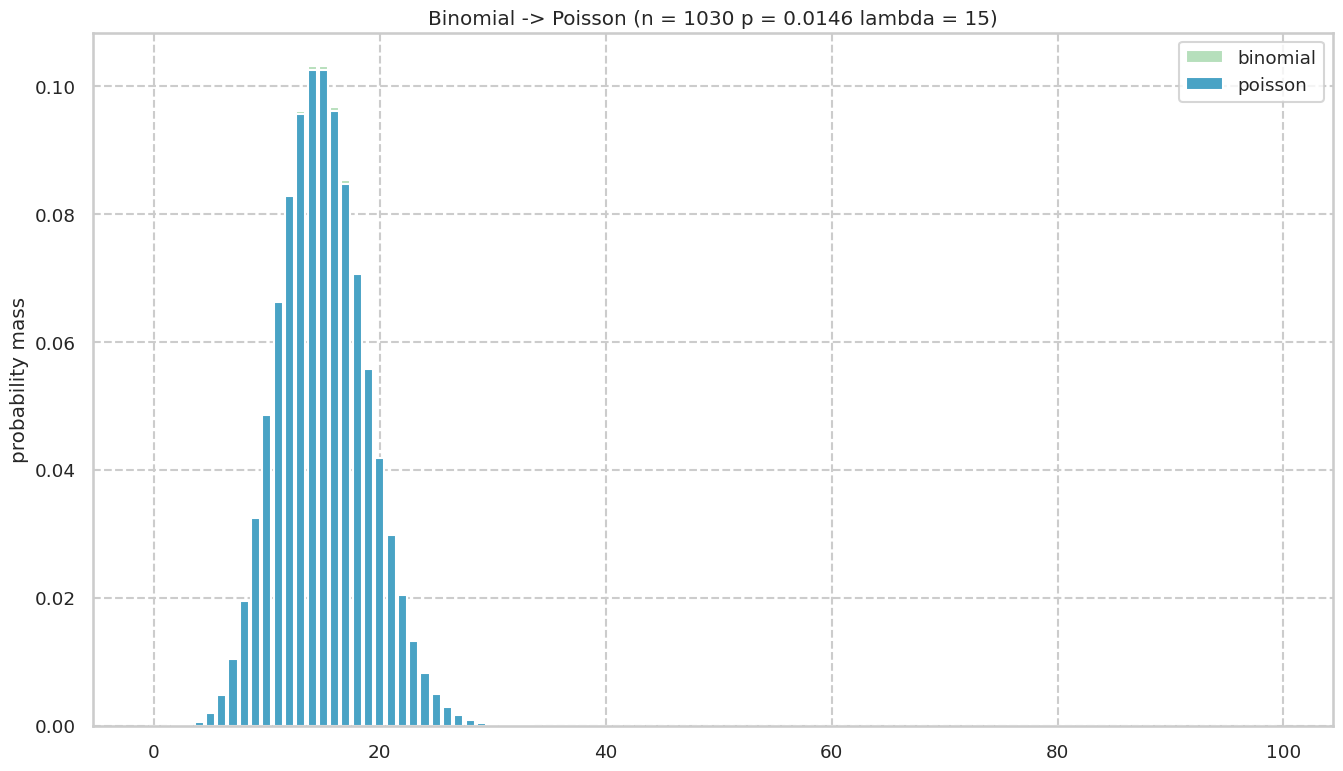
シュミレーション結果4

参考文献

Discussion