[大学数学] マクローリン展開の可視化

概要

無限微分可能な関数 $f(x)$ について, 多くの場合下記が成立する.

$$f(x)=\sum_{k=0}^\infty f^{(k)}(0)\frac{x^k}{k!}$$

ただし, $f^{(k)}(\cdot)$ はfのk階微分である. この式はテイラー展開を $a=0$ を代入すれば求められる.

以前下記の記事を書いていた時に, よく使う式だがどれぐらい近似できているか考えたことがないなと思い立ったのでPythonを用いて描画し, 検証することにした.

[統計学] ポアソン分布の期待値, 分散, 積率母関数, 最尤推定, 可視化

よく用いられる関数のマクローリン展開

せっかくなのでマクローリン展開を用いて関数を導出するところから始める.

指数関数

$$\begin{align*} &\text{When}\quad f(x) \coloneqq e^x, f'(x)=e^x \;f'(0)=1 \\ &\therefore \quad e^x = \sum_{k=0}^\infty \frac{x^k}{k!} \end{align*}$$

三角関数

三角関数のsin, cosはsin(0)が0になることを用いて導出をすることが出来る.

$$\begin{align*} \text{When} &\quad f(x) \coloneqq \sin (x), \\ f(x)&= \sin(0) \frac{x^0}{0!} + \cos (0) \frac{x^1}{1!} - \sin (0) \frac{x^2}{2!} - \cos (0) \frac{x^3}{3!} + \sin (0) \frac{x^4}{4!} + \cdots \\ &= \cos (0) \frac{x^1}{1!} - \cos (0) \frac{x^3}{3!} \cdots \\ &= \sum_{k=0}^\infty (-1)^k \frac{x^{2k+1}}{(2x+1)!} \end{align*}$$

$$\begin{align*} \text{When} &\quad f(x) \coloneqq \cos (x), \\ f(x)&= \cos(0) \frac{x^0}{0!} - \sin (0) \frac{x^1}{1!} - \cos (0) \frac{x^2}{2!} + \sin (0) \frac{x^3}{3!} + \cos (0) \frac{x^4}{4!} + \cdots \\ &= \cos(0) \frac{x^0}{0!} - \cos (0) \frac{x^2}{2!} + \cos (0) \frac{x^4}{4!} + \cdots \\ &= \sum_{k=0}^\infty (-1)^{k+1} \frac{x^{2k}}{(2k)!} \end{align*}$$

実装

Python言語を用いてマクローリン展開を図示してみる. 初めに必要なライブラリをimportする.

import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
import seaborn as sns

指数分布

指数分布のマクローリン展開は以下のようにPythonの関数にすることが出来る.

# toは何階まで微分するかを制御する
def f(x,to):
    ans = 0
    for k in range(to):
        ans = ans + x**k/np.math.factorial(k)
    return ans

試しにこの関数に適当な数を入れてみる. 指数関数は $x=1$ のときに以下のような値をとるので出力がこれに近いほどうまく近似できていることになる.

$$e = 2.71828182846...$$

f(1,100)
# 2.7182818284590455

実際に99階微分まで計算したところ, $x=1$ においては小数第10桁まで一致していることを確認できた. 次に指数関数と適当な $k$ を用いて近似した式をプロットして形状の変化を見る.

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 1, {"lines.linewidth": 4})
sns.set_palette("cool", 7, 0.8)

x = np.arange(-1, 3, 0.001)

fig=plt.figure(figsize=(16,9))
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Exponential approximation')
ax.set_ylabel('f(x)')

ax.plot(x, np.exp(x))
ax.plot(x, f(x,6))
ax.plot(x, f(x,5))
ax.plot(x, f(x,4))
ax.plot(x, f(x,3))
ax.plot(x, f(x,2))

ax.legend(['true','to=6','to=5','to=4','to=3','to=2'])

plt.show()

三角関数

三角関数についても描画のコードはおおよそ同じなので, マクローリン展開をした近似式をPythonの関数に起こした部分のみを掲載する

正弦関数

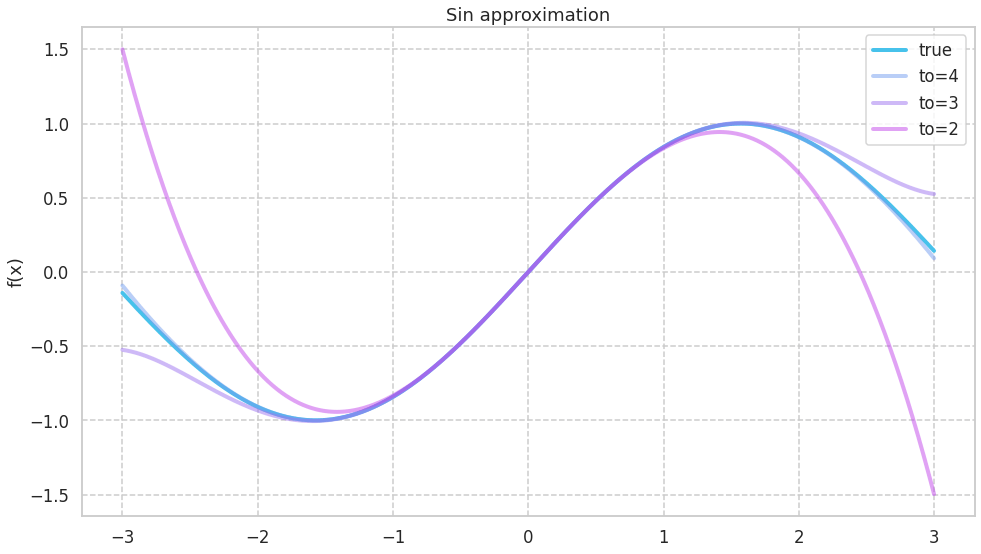
def f(x,to):
    ans = 0
    for k in range(to):
        ans = ans +((-1)**k) * (x**(2*k+1)/np.math.factorial(2*k+1))
    return ans

余弦関数

def f(x,to):
    ans = 0
    for k in range(to):
        ans = ans +((-1)**k) * (x**(2*k)/np.math.factorial(2*k))
    return ans

どの関数においても微分の回数を増やしていくごとに近似対象の関数の形に近づく様子が観察できた.