[統計学] ポアソン分布の期待値, 分散, 積率母関数, 最尤推定, 可視化

確率質量関数

$$f(x|\lambda)= \frac{\lambda^x e^{-\lambda}}{x!}$$

期待値・分散

指数関数のマクローリン展開

導出にあたり以下の式を用いるので先に証明する.

$$e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!} \cdots (1)$$

証明:

下記のマクローリン展開を実行する. なお, $f^{(k)}$ はfのk回微分とする.

$$\begin{align*} f(x) &= \sum_{k=0}^{\infty} f^{(k)}(0) \frac{(x-0)^k}{k!} \\ &= \sum_{k=0}^{\infty} f^{(k)}(0) \frac{x^k}{k!} \end{align*}$$

上式において $f(x)=e^x$ としたときに, $\forall k \in \N, f^{k}(0)=1$ が成り立つ. よって明らかに(1)式が成り立つ.

なお, マクローリン展開の詳細については別記事でまとめたので必要に応じて参照されたい.
マクローリン展開の可視化 | Shundeveloper

期待値

$$\begin{align*} \mathbb{E}(X) &= \sum_{x=0}^{\infty} x \cdot P(X) \\ &= \sum_{x=0}^{\infty} x \frac{\lambda^x e^{-\lambda}}{x!} \\ &= \sum_{x=0}^{\infty} x \frac{\lambda\lambda^{x-1} e^{-\lambda}}{x(x-1)!} \\ &= \lambda e^{-\lambda} \sum_{x=0}^{\infty} \frac{\lambda^{x-1}}{(x-1)!} \\ &= \lambda e^{-\lambda}e^\lambda \\ &= \lambda \end{align*}$$

分散

$$\begin{align*} \mathbb{E}(X^2) &= \sum_{x=0}^{\infty} x^2 \cdot P(X) \\ &= \sum_{x=0}^{\infty} \{x(x-1)+x\} \frac{\lambda^x e^{-\lambda}}{x!} \\ &= \sum_{x=0}^{\infty} x(x-1) \frac{\lambda^x e^{-\lambda}}{x!} + \sum_{x=0}^{\infty} x\frac{\lambda^x e^{-\lambda}}{x!} \\ &= \sum_{x=0}^{\infty} x(x-1) \frac{\lambda^2\lambda^{x-2} e^{-\lambda}}{x(x-1)(x-2)!}+\mathbb{E}(X) \\ &= \lambda^2 e^{-\lambda} \sum_{x=0}^{\infty} \frac{\lambda^{x-2}}{(x-2)!}+\mathbb{E}(X) \\ &= \lambda^2 e^{-\lambda}e^\lambda+\mathbb{E}(X) \\ &= \lambda^2+\mathbb{E}(X) \\ &= \lambda^2+\lambda \end{align*}$$

よって,

$$\begin{align*} \mathbb{V}(X) &= \mathbb{E}(X^2)-\mathbb{E}(X)^2 \\ &= \lambda^2 + \lambda - \lambda^2 \\&= \lambda \end{align*}$$

積率母関数

積率母関数(モーメント母関数)を用いると期待値・分散の導出が楽になることがあるが, ポアソン分布の場合どちらでも難易度はあまり変わらない印象である.

積率母関数の導出

積率母関数も指数関数のマクローリン展開を用いて導出する. なお, 5行目は可読性向上を目的として, 指数関数の表記に $\exp$ を用いている.

$$\begin{align*} Mx(t) &= \mathbb{E}(e^{tX}) \\ &= \sum_{x=0}^\infty e^{tx} \frac{\lambda^x e^{-\lambda}}{x!} \\ &= e^{-\lambda} \sum_{x=0}^\infty \frac{ (e^t\lambda)^x }{x!} \\ &= \exp{(-\lambda)}\exp{(e^t\lambda)} \\ &= e^{\lambda(e^t-1)} \\ \end{align*}$$

積率母関数を用いた期待値の導出

$$\begin{align*} \mathbb{E}(X) &= M_X(t)'\; |_{t=0} \\ &= \{\lambda(e^t - 1)\}' \cdot e^{\lambda(e^t-1)}\;|_{t=0} \\ &= \lambda e^t \cdot e^{\lambda(e^t-1)}\;|_{t=0} \\ &= \lambda e^0 \cdot e^{\lambda(e^0-1)} \\ &= \lambda e^0 \cdot e^{\lambda(1-1)} \\ &= \lambda e^0 \cdot e^{0} \\ &= \lambda \end{align*}$$

積率母関数を用いた分散の導出

3行目以降は, そのまま微分して, $t=0$ を代入する方法も可能だが, 以下のように $\mathbb{E}(X)$ に置き換えることで計算を楽にすることが出来る.

$$\begin{align*} \mathbb{E}(X^2) &= M_X(t)''\; |_{t=0} \\ &= \{\lambda e^t \cdot e^{\lambda(e^t-1)}\}' \;|_{t=0} \\ &= \{\lambda e^t\}' \cdot e^{\lambda(e^t-1)} + \lambda e^t \cdot \{e^{\lambda(e^t-1)}\}' \;|_{t=0} \\ &= \{\lambda e^t\}' \cdot e^{\lambda(e^t-1)} \;|_{t=0} + \lambda e^t \cdot \{e^{\lambda(e^t-1)}\}' \;|_{t=0} \\ &= \lambda e^t \cdot e^{\lambda(e^t-1)} \;|_{t=0} + \lambda e^0 \cdot \mathbb{E}(X) \\ &= \mathbb{E}(X) + \lambda \cdot \mathbb{E}(X) \\ &= \lambda + \lambda\cdot \lambda \\ &= \lambda+\lambda^2 \end{align*}$$

4行目第二項の微分の部分は, 積率母関数の一階微分なので, 期待値になる.

5行目第一項は積率母関数の一階微分した式になっているので期待値になる.

$$\begin{align*} \mathbb{V}(X) &= \mathbb{E}(X^2) -\mathbb{E}(X)^2 \\ &= \lambda + \lambda^2 - \lambda^2 \\ &= \lambda \end{align*}$$

最尤推定

対数尤度関数を導出する

$$\begin{align*} \ln L(\lambda) &= \ln P(\mathbf{x}) \\ &= \ln \prod_i P(x_i|\lambda) \\ &= \ln \prod_i \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} \\ &= \ln \prod_i \exp{\{ x_i \ln \lambda - \ln x_i! -\lambda \}} \\ &= \sum_i \biggl( x_i \ln \lambda - \ln x_i! -\lambda \biggr) \\ &= \sum_i x_i \ln \lambda - \sum_i \ln x_i! - n\lambda \end{align*}$$

対数尤度関数をパラメータで偏微分する

$$\begin{align*} \frac{\partial}{\partial \lambda}\ln L(\lambda) &= \frac{1}{\lambda} \sum_i x_i -n \end{align*}$$

よって $L(\lambda)$ を最大化する $\lambda_{ML}$ は,

$$\begin{align*} &\frac{1}{\lambda_{ML}} \sum_i x_i -n = 0 \\ &\frac{1}{\lambda_{ML}} \sum_i x_i = n \\ &\frac{1}{n} \sum_i x_i = \lambda_{ML}. \end{align*}$$

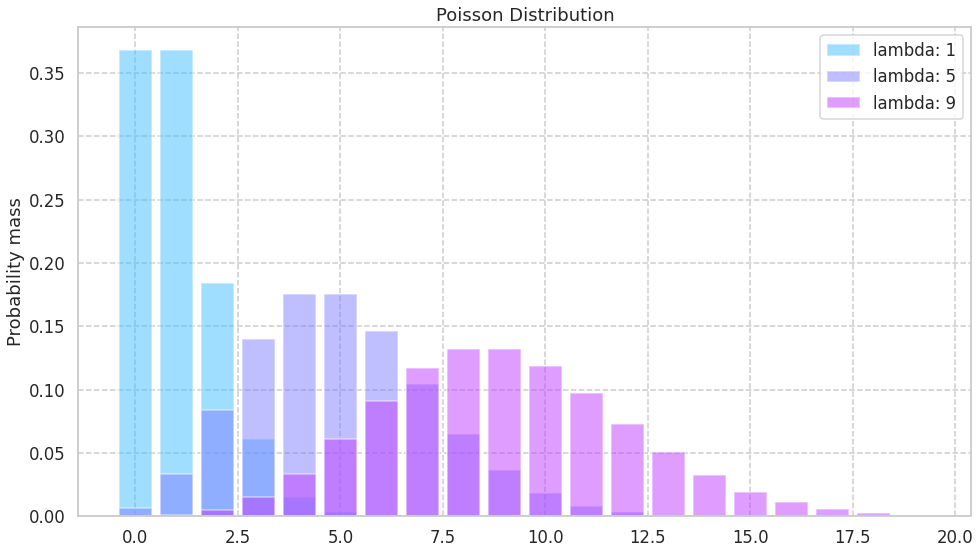
可視化

ポアソン分布のパラメータを変えたときの様子を可視化します. コードは seabornのドキュメント を参考に作成しました

期待値も分散も $\lambda$ なので, パラメータが大きくすれば, 平均もばらつきも大きい分布に変化すると考えられます.

以下コード

import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt
import seaborn as sns

sns.set()
sns.set_style("whitegrid", {'grid.linestyle': '--'})
sns.set_context("talk", 1, {"lines.linewidth": 4})
sns.set_palette("cool", 3, 1)

x = np.arange(0, 20, 1)

fig=plt.figure(figsize=(16,9))
ax = fig.add_subplot(1, 1, 1)
ax.set_title('Poisson Distribution')
ax.set_ylabel('Probability mass')

bar = [
    ax.bar(
        x, poisson.pmf(x, lambda_), alpha=0.5
    )
    for lambda_ in range(1, 13,4)
]

ax.legend(['lambda: '+ str(lambda_) for lambda_ in range(1,13,4)])

plt.show()

参考文献

(1) 竹村彰通.”新装改訂版 現代数理統計学”.2020.学術図書出版社
(2) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定準1級対応 統計学実践ワークブック”.2020.学術図書出版社
(3) 一般社団法人 日本統計学会.”日本統計学会公式認定 統計検定1級対応 統計学”.2013.東京図書出版社
(4) C.M.ビショップ.”パターン認識と機械学習 上 ベイズ理論による統計的予測”.2019.丸善出版株式会社