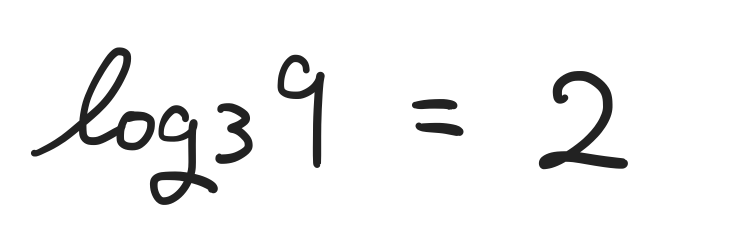
対数の定義
まず、こんなかんじで指数を使った式がある。
これについて、こう書き直したものを対数という。
この場合はつまり、3を何乗したら9になる? → 2 ということ。
この3の部分を 底 という。
(9の部分を 真数 というらしいが、あまり聞かない)
特殊な対数
常用対数
底が 10 の対数を 常用対数 という。
つまるところ、10進法において桁の数を表す。
たとえばこんなふうになったら
\log_{10}{x} = 2.5741\cdots
x は 100 と 1000 の間、つまり3桁の数だとわかる。
自然対数
底がネイピア数 eの対数を 自然対数 という(逆にネイピア数のことを 自然対数の底 とも呼ぶ)。
表記
自然対数の表記は3通りある。
\begin{align*}
&\log_e{x} \\[0.5em]
&\log{x} \\[0.5em]
&\ln{x} \\[0.5em]
\end{align*}
意味は全て同じで \log{x} か \ln{x} がよく用いられる。
対数の計算
定理
\begin{align*}
&\text{定理 1 :} \quad \log_a{x^y}=y\log_a{x} \\[0.5em]
&\text{定理 2 :} \quad \log_a{xy}=\log_a{x} +\log_a{y} \\[0.5em]
&\text{定理 3 :} \quad \log_a{\frac{x}{y}}=\log_a{x} -\log_a{y} \\[0.5em]
&\text{定理 4 :} \quad \log_a{x}=\frac{\log_c{x}}{\log_c{a}} \quad {\footnotesize (\text{ただし } c \text{ は以外の任意の正の数})}
\end{align*}
定理の導出
定理1: \log_a{x^y}=y\log_a{x} の導出
これは導出というか、対数の定義をみれば「そらそうやろ」となる。
\text{対数の定義 :} \quad a^b=x \quad \rightleftarrows \quad \log_a{x}=b
なわけだから、
a^{by}=x^y \quad \rightleftarrows \quad \log_a{x^y}=by
b=\log_a{x} だから、
定理2: \log_a{xy}=\log_a{x} +\log_a{y} の導出
\log_a x=X, ~ \log_a y=Y とすれば x=a^X, ~ y=a^Y なので、
\begin{align*}
\log_a{xy}&=\log_a{a^X a^Y}\\[0.5em]
&=\log_a{a^{X+Y}}\\[0.5em]
&=(X+Y)\log_a{a}\\[0.5em]
&=X+Y\\[0.5em]
&=\log_a{x}+\log_a{y}
\end{align*}
定理3: \log_a{\frac{x}{y}}=\log_a{x} -\log_a{y} の導出
定理2と同じこと。
\log_a x=X, ~ \log_a y=Y とすれば x=a^X, ~ y=a^Y なので、
\begin{align*}
\log_a{\frac{x}{y}}&=\log_a{\frac{a^X}{a^Y}}\\[0.5em]
&=\log_a{a^Xa^{-Y}}\\[0.5em]
&=\log_a{a^{X-Y}}\\[0.5em]
&=(X-Y)\log_a{a}\\[0.5em]
&=X-Y\\[0.5em]
&=\log_a{x}-\log_a{y}
\end{align*}
定理4: \log_a{x}=\frac{\log_c{x}}{\log_c{a}} の導出
a^{b}=x の両辺の対数をとると
\begin{align*}
\log_c{a^{b}} &= \log_c{x} \\[0.5em]
b \log_c{a} &= \log_c{x} \\[0.5em]
b &= \frac{\log_c{x}}{\log_c{a}}
\end{align*}
対数の定義 : \quad a^b=x \quad \rightleftarrows \quad \log_a{x}=b \quad なわけだから、
\log_a{x}=\frac{\log_c{x}}{\log_c{a}}
対数関数の微分
https://zenn.dev/shintarot/articles/820b211c7d64c5
対数を応用した計算
両辺の対数をとる
a=b \quad ならば当然 \quad \log_c a=\log_c b \quad ( c は 1 以外の任意の正の数) だ。
これを利用して計算することを、「両辺の対数をとる」といって、指数を下に降ろしたいときなど便利。
ただ、たとえば \log_1{3} という数は存在しない( 1 を何乗しても 3 にはならない)ので、 c は 1 以外の任意の正の数という制限がある。
例題
3^x=5^{2x+1} のとき x を求める。
両辺の対数をとると、
\begin{align*}
\log{3^x} &= \log{5^{2x+1}} \\[0.5em]
x\log{3} &= (2x+1)\log{5} \\[0.5em]
&= 2x\log{5} + \log{5} \\[0.5em]
x\log{3} - 2x\log{5} &= \log{5} \\[0.5em]
x(\log{3}-2\log{5}) &= \log{5} \\[0.5em]
x &= \frac{\log{5}}{\log{3} - 2\log{5}} \\[0.5em]
&= \frac{1}{\frac{\log{3}}{\log{5}}-2} \\[0.5em]
&= \frac{1}{\log_5{3} - 2}
\end{align*}
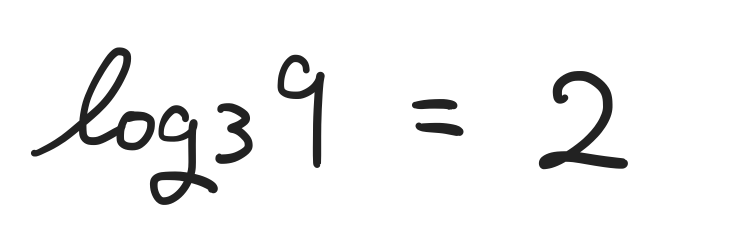
Discussion