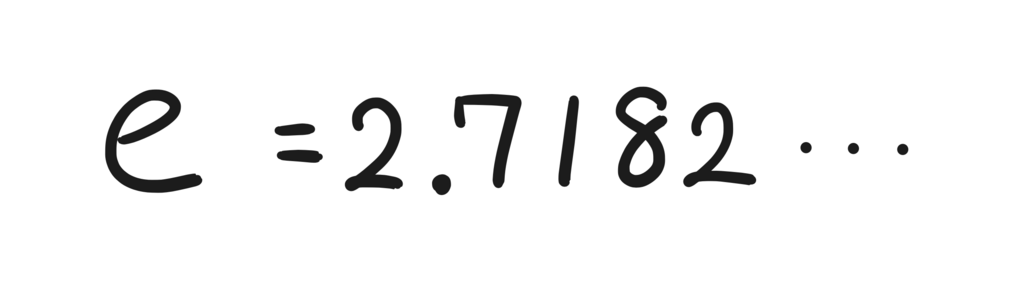
ネイピア数の定義
\text{定義 :} \quad \text{ネイピア数 }e=\lim_{n \to \infty}(1+\frac{1}{n})^n
つまり、 1 よりほんのわずかばかり大きい数を無限に自乗したもの 。
なんとなく (1+0)^\infty で 1 になりそう...な気もするが、実際は
e=2.7182\cdots
という絶妙な値の無理数となる。
ネイピア数の指数関数
これはよくみる形。グラフを描くとこうなる。
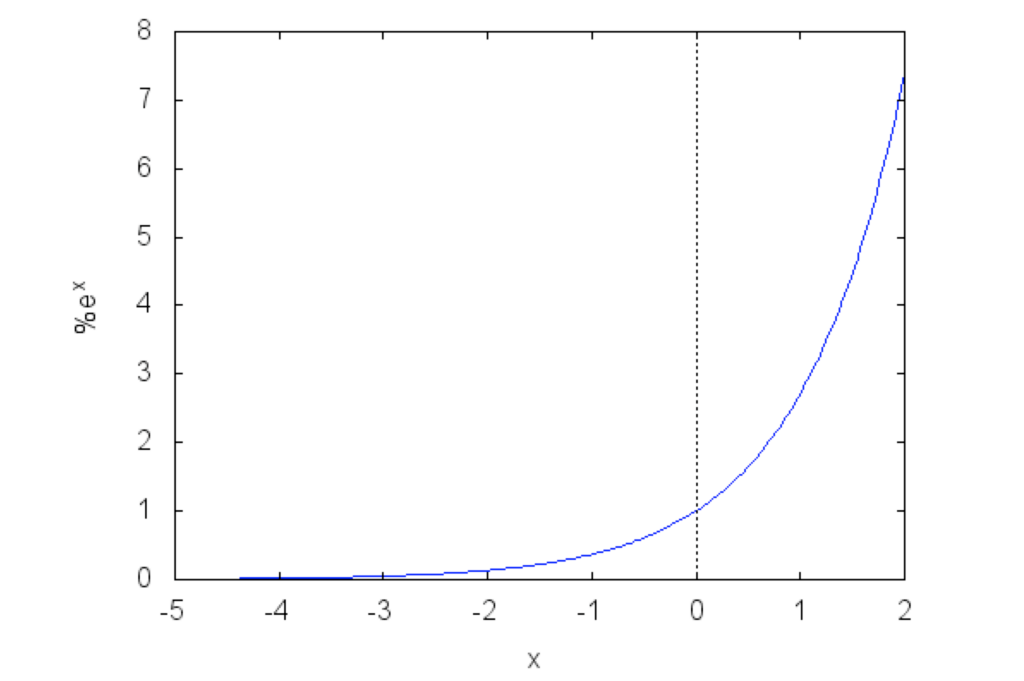
f(x)=e^x
f(x)=e^\frac{1}{x}(ただし x>0 )

f(x)=e^(1/x) ただし x>0
ネイピア数の指数関数の微分
ネイピア数の指数関数は微分しても変わらない。
不思議な感じがするが、そもそも不思議な成り立ちの数なので納得できる気もする(?)
証明してみた↓
ネイピア数の指数関数の導関数を求める
微分するとは、導関数を求めるということである。
導関数の定義は
\text{定義 :} \quad f(x) \text{ の導関数 } \displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}
で、今回は f(x)=e^x の導関数を求める。
\begin{align*}
f'(x)&=\lim_{h \to 0}\frac{e^{x+h}-e^x}{h} \\[1em]
&=\lim_{h \to 0}\frac{e^{x}e^{h}-e^x}{h} \\[1em]
&=e^{x}\lim_{h \to 0}\frac{e^{h}-1}{h}
\end{align*}
ここで e の定義は \displaystyle e=\lim_{n \to \infty}(1+\frac{1}{n})^n なので、
\displaystyle f'(x)=e^{x}\lim_{h \to 0}\frac{(\displaystyle \lim_{n \to \infty}(1+\frac{1}{n})^n)^{h}-1}{h}
n \to \infty ならば \frac{1}{n} \to 0 だから \frac{1}{n}=h , n=\frac{1}{h}
\begin{align*}
\displaystyle f'(x)&=e^{x}\lim_{h \to 0}\frac{(\displaystyle \lim_{n \to \infty}(1+h)^\frac{1}{h})^{h}-1}{h} \\[1em]
&=e^{x}\lim_{h \to 0}\frac{((1+h)^\frac{1}{h})^{h}-1}{h}=e^{x}\lim_{h \to 0}\frac{(1+h)-1}{h}=e^{x}\lim_{h \to 0}\frac{h}{h} \\[1em]
&=e^x
\end{align*}
と求まった。というかそもそもこうなるように e を定義したんじゃないかという気がする。
おまけ: f(x)=e^\frac{1}{x} の微分
\text{定理 :} \quad \displaystyle\frac{d}{dx}e^\frac{1}{x}=-\frac{e^\frac{1}{x}}{x^2}
これは合成関数の微分をつかえばよい。
\displaystyle \frac{1}{x}=u とおく。
\begin{align*}
\frac{de^u}{dx}&=\frac{de^u}{du}\frac{du}{dx}\\[1em]
&=e^u\times -\frac{1}{x^2}
\end{align*}
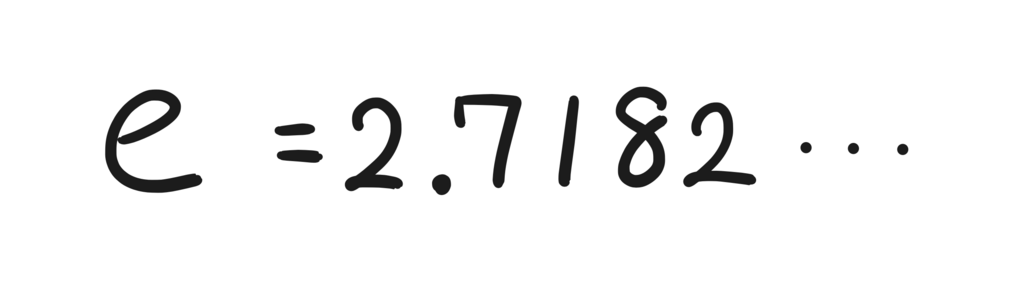


Discussion