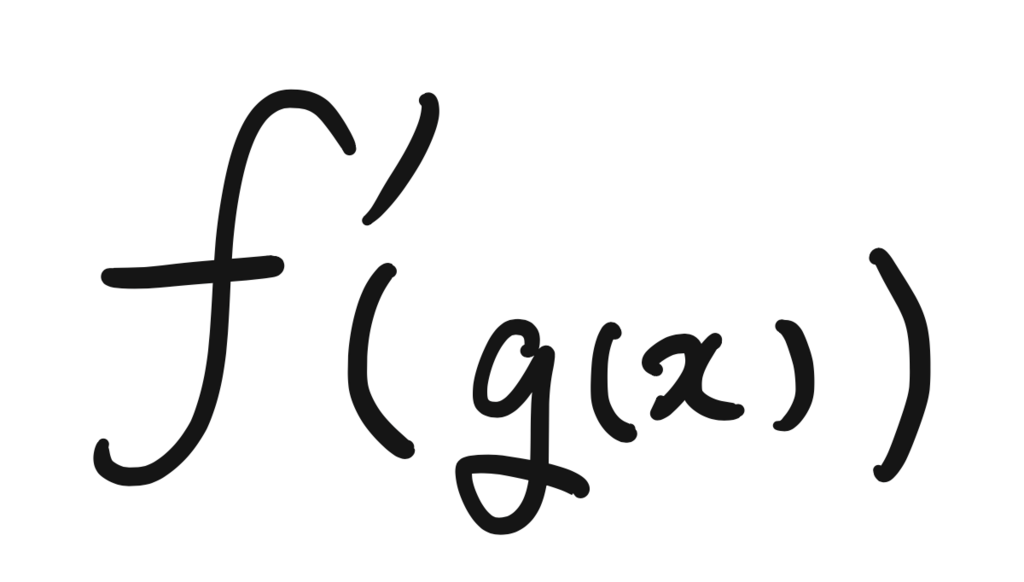
合成関数とは
となるような関数のこと。この f(g(x)) を x で微分するにはどうするのか。
合成関数の微分
連鎖律 (Chain Rule) とも呼ぶ。
定理
定理というかただの式変形だけど。
\text{定理 :} \quad \frac{d}{dx}f(g(x))=\frac{d}{dg(x)}f(g(x))\times\frac{d}{dx}g(x)
説明
まず f(g(x)) を x で微分するとそのまま書く。
これに \displaystyle \frac{dg(x)}{dg(x)}=1 をかけるとこう表せる。
\frac{df(g(x))}{dx} \quad = \quad \frac{df(g(x))}{dx}\times\frac{dg(x)}{dg(x)} \quad = \quad \frac{df(g(x))}{dg(x)}\times\frac{dg(x)}{dx}
これで素直に微分できる。わかりにくければ、 g(x)=y とおいてみれば見やすくなる。
\frac{df(y)}{dx} \quad = \quad \frac{df(y)}{dy}\times\frac{dy}{dx}
例題
\begin{cases}
f(y)=y^2 + 3y \\[0.5em]
y=x^3
\end{cases}
f(y) を x で微分する。
\begin{align*}
\frac{df(y)}{dx} &= \frac{df(y)}{dy} \times \frac{dy}{dx} \\[0.5em]
&= (2y+3) \times 3x^2 \\[0.5em]
&= (2x^3+3) \times 3x^2 \\[0.5em]
&= 6x^5+9x^2
\end{align*}
Discussion