「分布」を考える

前提知識
分布ってなんだ
「分布」というと、どんなものを思い浮かべるだろう?
ポケモンずかんには、ポケモンごとにせいそくちの「分布」が載っていた。
「分布」を辞書で引いてみた。
分かれてあちこちにあること。(スーパー大辞林3.0)
なるほど、こういうイメージだ。
これは位置を表すのに2つの値が必要な、つまり2次元の分布といえる。
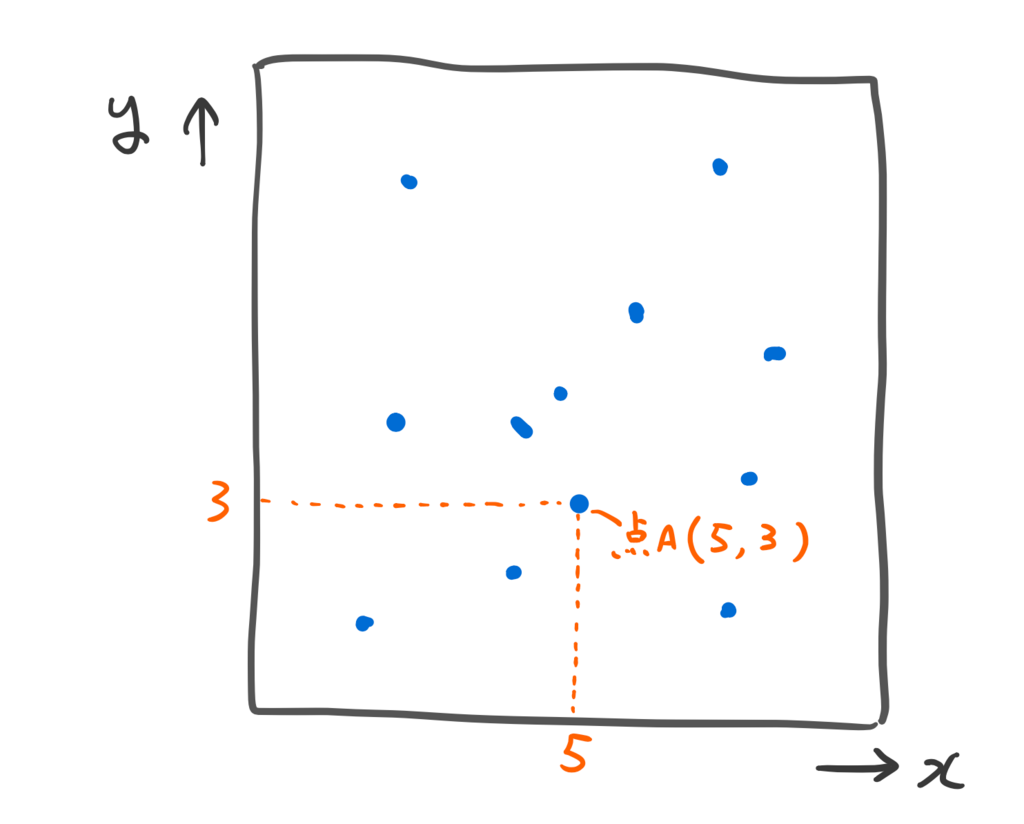
単純化のために1次元の分布を考えると、こんなかんじになる。

1次元の分布を考える
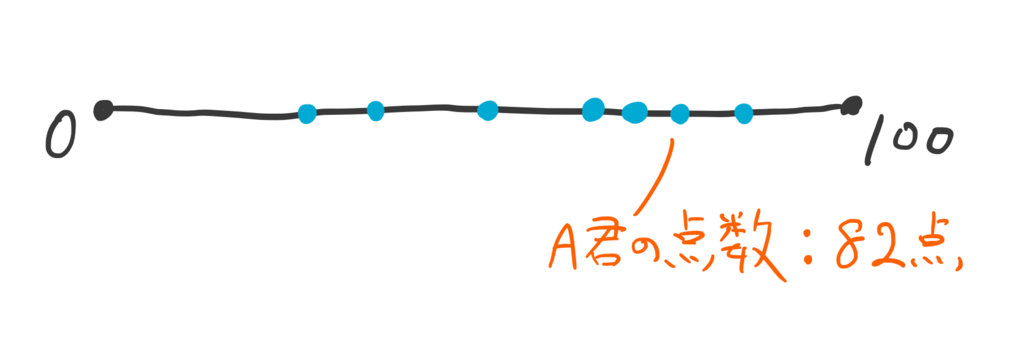
1次元の分布として、「テストの点数の分布」を考える。
あるテストを7人が受けたとき、点数の分布はこんなかんじで、A君の点数は82点だった。
これがもし、200人がこのテストを受けていたらこんなかんじになる(青い点の数は200もないが、200あることにしてください)。
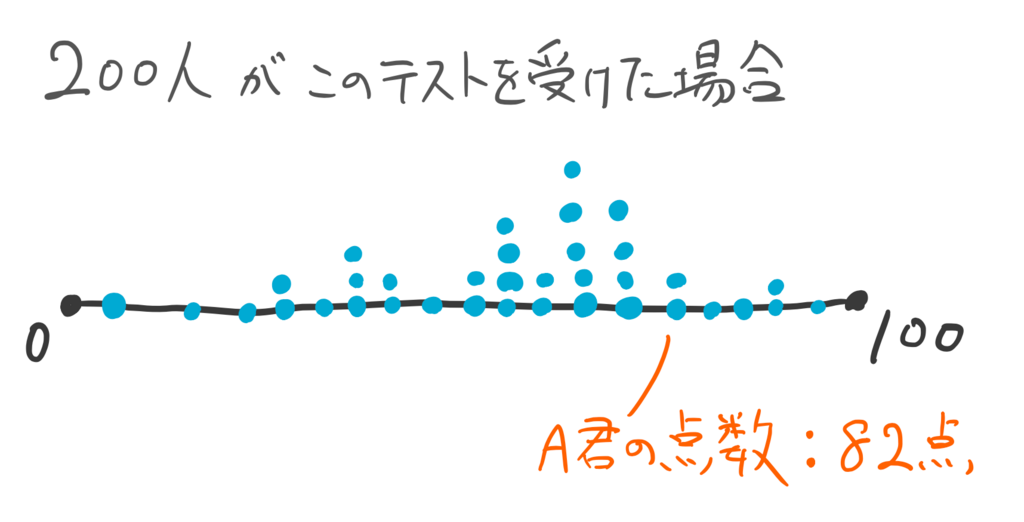
200人も同じテストを受けていれば、同じ点数の人が複数いることもあるだろう。82点をとった人はA君含め2人いる。
この青い点は分布そのものなわけだが、「何点を取った人は何人いる」ということを表す山になっている。この山の形をグリーンの点線でかたどる。
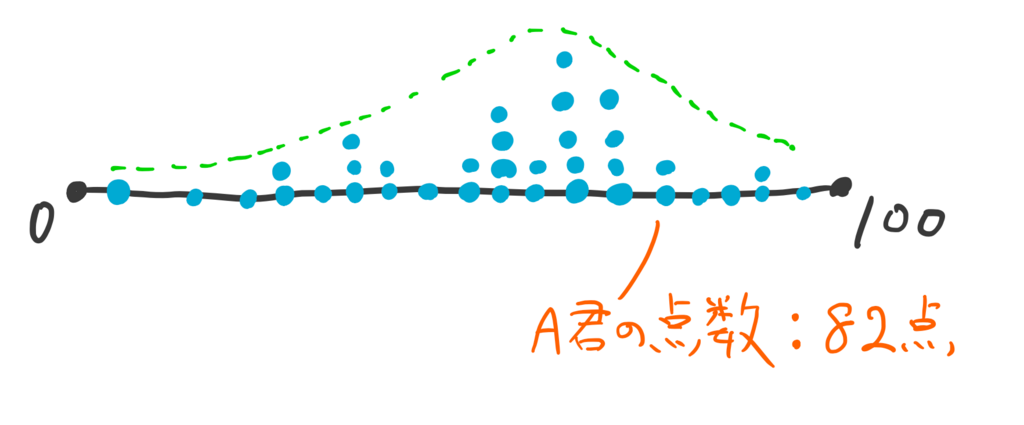
こうなる。

「点数」と「人数」の2次元に
このグリーンの線は「なめらかな線」だから、関数で表したい。
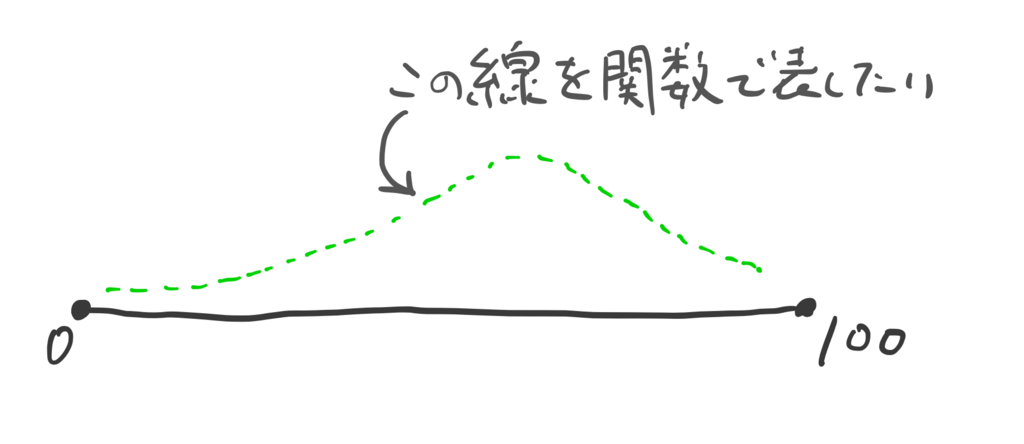
この関数はつまり
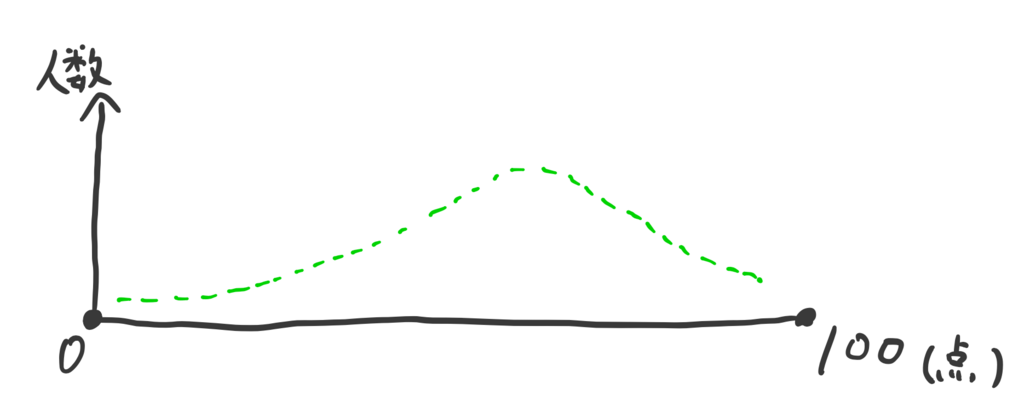
この関数が得られれば、たとえば「37点の人は何人?」とか「90点以上の人は全体の何%?」という計算がすぐできるし、その他いろいろ統計的な分析ができる。
確率密度関数
このグリーンの線をあらわす関数を 確率密度関数(Probability Density Function; PDF) という。
この関数は、毎回分布をプロットしてから計算で出すものではない。
そうではなく、「代表的な分布」というのがひな型で何種類か用意されているので、今回の分布はそのどれに近いかな?という当てはめ方をする。
(もちろん、なんとなく見た目がこれに似てる、とかいうだけでなく、条件をあてて判定する。)
そして、たとえば「今回の分布は正規分布を当てはめてよいだろう」となれば、
今回の分布は 正規分布に従う という表現をする。そして、それ以降はその分布を正規分布として扱う。
いろいろな分布とその確率密度関数
正規分布 (Normal Distribution)
もっとも基本的な分布が、この正規分布。 ガウス分布 (Gaussian Distribution) とも呼ばれる。また世の中の「誤差」は一般的にこの分布に従うことが知られており、そのため 誤差分布 (Error Distribution) と呼ばれることもある。
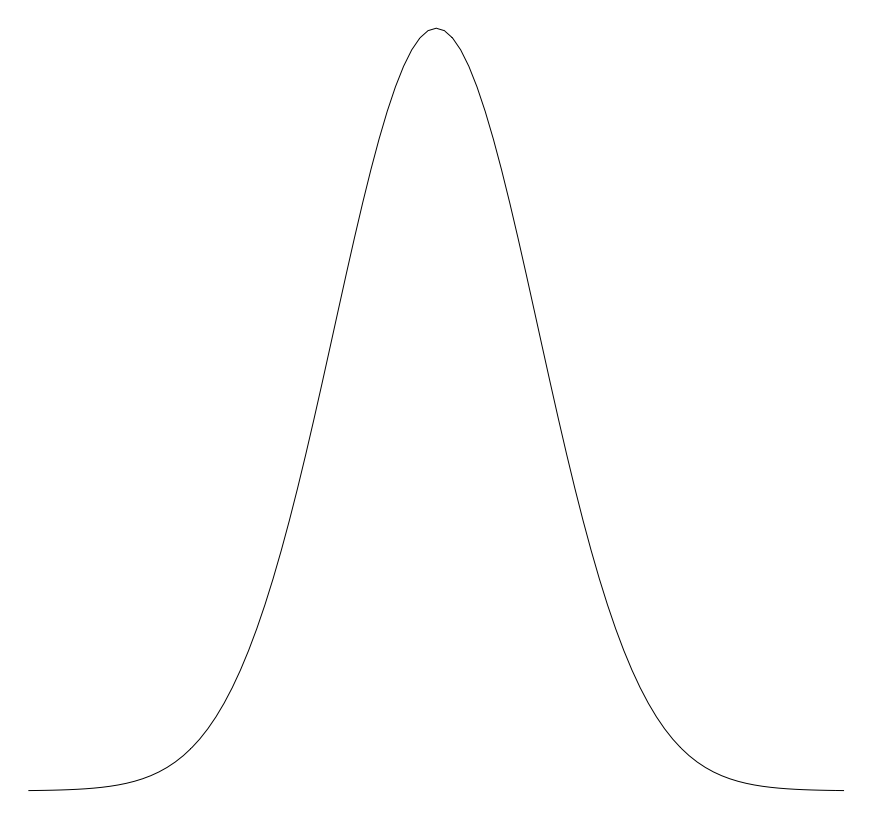
世の中のテストの点数の分布はこの正規分布に従うとされており、いわゆる「偏差値」もこれを前提に計算される。
確率密度関数は以下。
サンプルの取り得る値を
ほかの分布
coming soon...
累積分布関数 (Cumulative Distribution Function; CDF)
サンプルの値がある値以下をとる確率を表す関数を累積分布関数という。
たとえば

定義はこうなる。
Discussion