平均とは

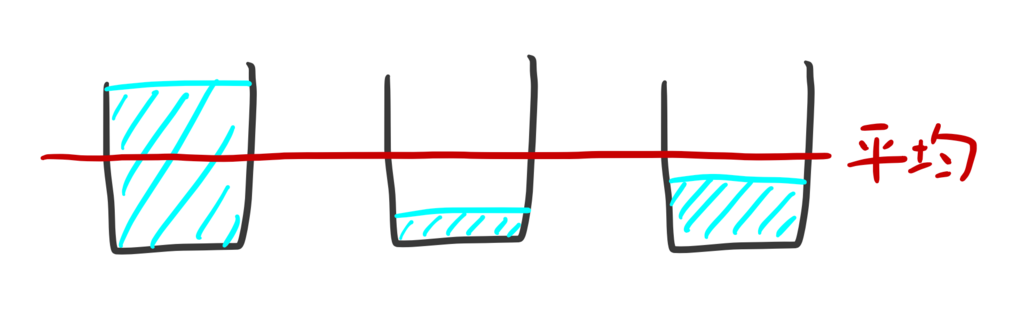
「平均」とは日常でもよく聞く言葉だが、どういう意味なんだろう...。

なんとなく、「真ん中の値」というイメージがあるだろう。実際そんなイメージでOKだ。しかし、「真ん中の値」の測り方は平均以外にもいくつかあるし、平均の算出方法にもいろいろある。

平均の概念

平均とは、「みんなあわせてこの値だから、ひとつあたりいくら」という考え方。

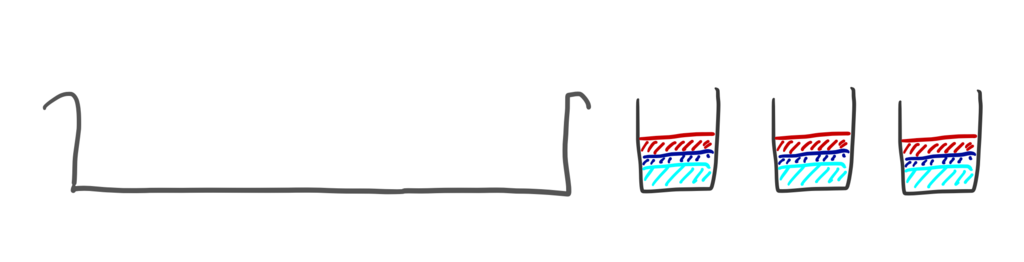
たとえばこんなふうに中の水の量がバラバラのコップが３つあるとする。

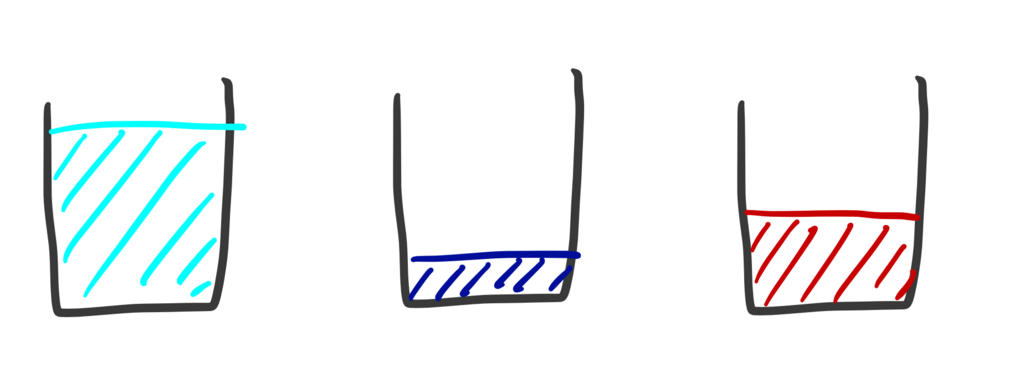
これを 平均 するにはどうすればよいか。

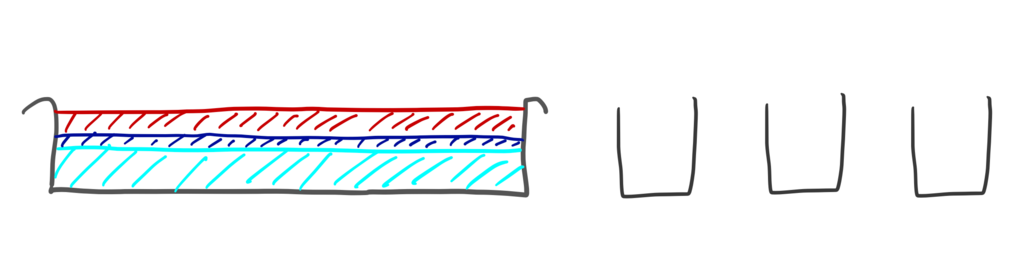
まずいったん、大きなたらいにでも水を集める。

こうなる。

それから、均等にコップに水を戻せば、

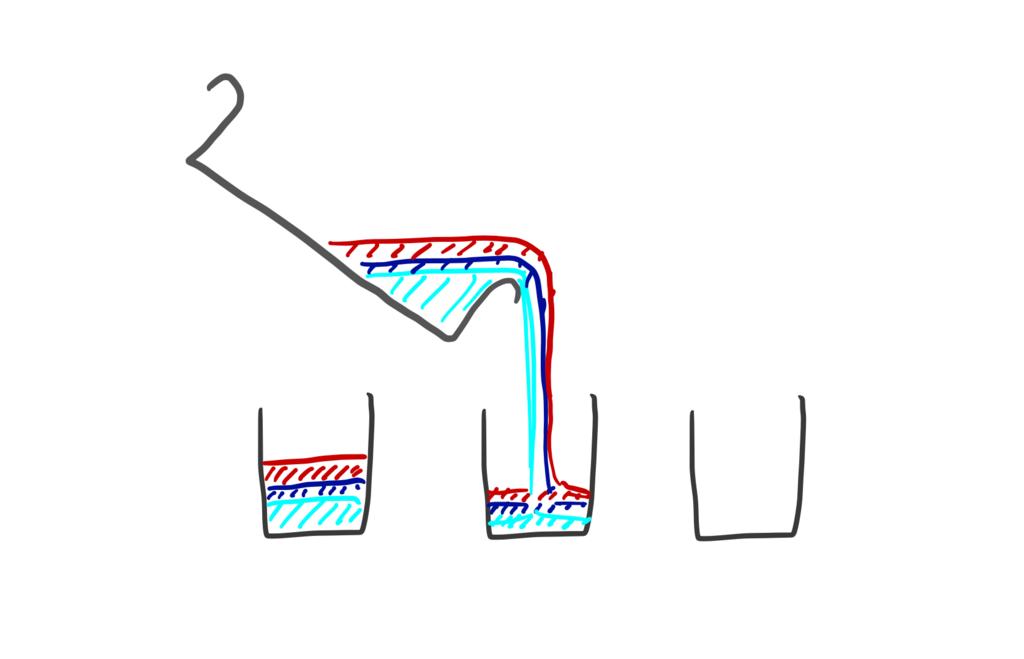
これで 平均 できた。

このように、平均とは

1. 全てをいったん一つに合わせて
2. 一つあたりに戻す

ことによって求まる。

そして どうやって「合わせて、戻す」か によって方法がわかれる。

平均の種類

相加平均

加法平均 や 算術平均 とも呼ばれる。最も一般的な平均法で、ふつう、ただ「平均」といえばこれを指す。

具体的な方法は

1. 全てをいったん一つに 足し 合わせて
2. 一つあたりに戻す（足した分だけ割る）

例

テストの点数が

• Aくん：7点
• Bくん：4点
• Cくん：8点

のとき、平均点を求める。

この相加平均はこうなる。

$$\text{相加平均} = (7+4+8) \times \frac{1}{3}$$

ということで、だいたい6.3点となった。

一般化すればこうなる。

$n$ 個のサンプルの相加平均は、 $n$ 番目のサンプルの値を $a_n$ とすると、

$$(a_1 + a_2 + \cdots + a_n)\times \frac{1}{n}$$

相乗平均

乗法平均 や 幾何平均 ともよばれる。

具体的な方法は

1. 全てをいったん一つに 掛け 合わせて
2. 一つあたりに戻す（掛けた分だけルートにいれる）

若干ピンとこないかもしれないが、例えば $2\times 2\times 2$ つまり $2^3$ を元に戻すには $\sqrt[3]{2^3}$ とすればよい。

例

テストの点数が

• Aくん：7点
• Bくん：4点
• Cくん：8点

のとき、平均点を求める。

この相乗平均はこうなる。

$$\text{相乗平均} = (7\times 4\times 8)^\frac{1}{3}$$

ということで、だいたい6.07点くらいになった。

一般化すればこうなる。

$n$ 個のサンプルの相乗平均は、 $n$ 番目のサンプルの値を $a_n$ とすると、

$$(a_1 \times a_2 \times \cdots \times a_n)^\frac{1}{n}$$

その他の平均

ほかにも「調和平均」があるし、「加重平均」という言葉もある（加重平均は平均の種類ではない気がするし、べつに概念を知らなくても考えればわかることと思う）。
これらについてはまた今度。